® APPLICATION BULLETIN Mailing Address: PO Box 11400 • Tucson, AZ 85734 • Street Address: 6730 S. Tucson Blvd. • Tucson, AZ 85706 Tel: (602) 746-1111 • Twx: 910-952-111 • Telex: 066-6491 • FAX (602) 889-1510 • Immediate Product Info: (800) 548-6132 OPERATIONAL AMPLIFIER MACROMODELS: A COMPARISON By Bonnie Baker (602) 746-7468 All major competitors in the operational amplifier markets are providing their customers Spice-based macromodels. These models give the designer a tool to do initial character- ization and a limited amount of system troubleshooting. In the interest of faster simulation times and lower CPU memory requirements, macro topologies have been developed to simulate a majority of the op amp’s performance character- istics. Several different approaches to creating macromodels have been used, each producing a macro with its own set of strengths and weaknesses. Circuit simulations have become increasingly important to the systems level designer. By using macros, the designer can quickly determine gross limitations of their design and correct potential problems in the circuit quickly at the computer terminal. Although it is not recommended that circuit simulation replace the bread board, many costly design problems can be quickly identi- fied during the simulation cycle. By using a macromodel as a simulation tool, the designer may be able to shorten the design cycle of their circuit. This, of course, assumes that the model’s level of accuracy is adequate for the design’s constraints and trade offs. If the systems designer is aware of the capabilities and limitations of the macro that has been selected for the simulation phase, the entire design cycle can be significantly reduced. Many of the macro’s limitations can also be overcome with easily implemented enhance- ments to the basic macromodel architecture, depending on the specific application requirements. A good selection of the correct model with appropriate enhancements enables the designer to use the op amp macromodel as an effective tool in system level circuit design. Historically, circuit simulation tools, such as SPICE(1), were developed for the integrated circuit designer. SPICE uses detailed mathematical formulas, which emulate the behavior of actual devices. The IC designer uses simulation tools, such as SPICE, extensively during the circuit design cycle. The level of sophistication that the IC circuit designer requires is that every element is simulated as closely to actual performance as possible. As a consequence, the ma- jority of elements in the simulated circuit are non-linear elements, such as bipolar transistors, field-effect transistors, etc. Because of the complex behavior of these non-linear elements in the Spice simulation environment, these ele- ments require more simulation time and computer memory. With increased integrated circuit complexity, performance and size, simulation time and computer memory have be- come critical simulation constraints for the software and systems used by the IC designer. This limitation has prevented the systems level designer from taking full advantage of the same simulation tools. As a result, macros have gained popularity as an alternative tool for circuit simulation at the systems level. Op amp macros are designed to model specific, predetermined amplifier characteristics. When Spice is used as the preferred soft- ware, the op amp macro is typically developed with one of two basic design approaches. ISS RP D1 + V5 V3 + D2 D3 + V4 +In –In 14 J1 J2 15 C1 16 R3 R4 + V7 V+ 22 Out D4 D5 R2 C2 R1 C3 + V6 RO1 G1 R5 G2 + V1 + V2 + V8 G3 V– FIGURE 1. Boyle Macromodel Used to Simulate Operational Amplifiers. ©1993 Burr-Brown Corporation AB-046 Printed in U.S.A. March, 1993 SBOA027 

MACROMODEL DESIGN APPROACHES The first basic macromodel design approach involves reduc- ing the complexity of the circuit. For example, the input stage of an op amp can be reduced to a differential pair with a resistive load, biased with a current source. The actual op amp could have a cascoded differential input with active load and the current source biasing the input stage would be built using a transistor that would have the non-linearities associated with early voltage and collector resistance, etc. Throughout the macromodel circuit, transistors that are deemed non-critical are replaced with linear elements, such as current sources, resistors, etc. The reduction in complex- ity reduces the number of nodes in the circuit as well as the number of non-linear devices, both of which will reduce simulation time. To reduce simulation time even further, the transistors are as near to ideal as possible. This is done by reducing the number of transistor model parameters. The obvious benefit of this macromodel design approach is a reduction in simulation time; however, op amp performance is compromised to some extent. For example, the input stage of the model described does not model the common-mode input range of the amplifier properly. A second method that is used in macromodelling is the build method. When this method is used, the designer of the macro characterizes the performance of the op amp and then builds the macro out of ideal linear elements, such as resistors, inductors, capacitors, dependent sources and independent sources. A good example of this topology would be the op amp hybrid pi-model where the input stage of the amplifier is a resistor. The voltage across that resistor is sensed by the gain stage, etc. The simulation time of this type of model is significantly faster than the first macromodel design method; however, the op amp performance is compromised to a great extent with this approach. THE BOYLE OP AMP MACROMODEL The Boyle Op Amp Macromodel(2) was designed using the simplification method to design the input stage and the build method for the remainder of the macro design. As shown in +In –In ISS R1 R2 CDIF VOS J1 J2 5 6 C1 R3 R4 V1 G1 G3 G5 C8 L1 G7 R13 G9 C2 R5 R7 C4 R9 C6 R11 D1 D2 V2 21 71 31 41 51 R14 L3 G2 G4 G6 C3 R6 R8 C5 R10 C7 G8 R15 L4 G10 R12 C9 L2 R16 7 R17 61 R18 4 Input Stage Gain Stage Center Reference Pole Stage Pole/Zero Stage Zero/Pole Stage Common-Mode Gain Stage 7 4 D3 D4 G11 D5 G12 D7 D8 91 D6 Ouput Stage G13 V93 V94 R19 L3 G14 R20 Out V+ V– FIGURE 2. MPZ Op Amp Macromodel Blocks. Duplicate phase blocks are allowable in the macromodel design. 2 

Figure 1, the only transistors in the Boyle model are used for the input differential pair of the op amp. All other elements are linear devices with the exception of a few diodes that are used as clamps. The ac parameters that this model topology simulates are slew rate, unity gain frequency, gain/phase for a one or two pole amplifier and a simplified ac output resistance. DC characteristics modelled are quiescent cur- rent, short circuit output current, output voltage swing maxi- mums and minimums, input bias current, common-mode rejection ratio, and dc output resistance. The Boyle macromodel performance characteristics listed above suf- fice for many general applications. However, temperature performance, common-mode input range, offset voltage, offset current, input protection, power supply rejection, noise, THD, input impedance, good ac output resistance, and change in supply current versus supply voltage are a few of the more important parameters that are not modelled with the Boyle macro topology. Several op amp vendors have chosen to design their macros around the Boyle topology. Of the companies using the Boyle model that were researched, all added enhancements to the Boyle model to include a few more operational amplifier performance features. THE MULTIPLE POLE/ZERO MACROMODEL Another popular topology using both macromodelling meth- ods is shown in Figure 2. The model shown in Figure 2 and the Boyle model (Figure 1) have identical input stages, but all of the remaining stages are different. This topology evolved from several sources(3,4) and is named after the mid- section of the model, multiple pole/zero or MPZ. The mid- section of this model can be expanded to include additional poles, pole-zero, or zero-pole stages. The MPZ macro has the same dc performance characteristics as the Boyle model as well as input offset bias current, input offset voltage and input differential impedance. The ac parameters that this model topology simulates are slew rate, unity gain fre- quency, gain/phase for a multiple pole/zero amplifier, CMRR versus frequency, and a simplified ac output resistance. In addition, the MPZ macro models change in quiescent cur- rent versus change in supply voltage, has no ground refer- ence, and splits the output current between the supplies instead of sinking and sourcing from ground. A few of the MPZ limitations are a lack of temperature performance, poor modelling of common-mode input range, no input protection circuitry, no power supply rejection, no noise, no THD, and the ac output resistance is modelled with a one zero system. THE BOYLE MACROMODEL VERSUS THE MPZ MACROMODEL When comparing op amp macro performance, there are two simulation characteristics that are critical to the systems designer. The macro must model the electrical performance of the op amp in the designer’s application of interest, and secondly, the macro must perform the simulation in a rea- sonable amount of time using a reasonable amount of com- puter memory. When comparing the electrical performance of the Boyle model versus the MPZ model, the MPZ model provides several additional performance characteristics that the Boyle does not. For instance, the MPZ model models the same DC parameters that the Boyle model does and additionally input offset voltage and input offset bias current. The MPZ macro lacks a reference to ground which is sometimes convenient in level shift circuits where the Boyle model has several ground references in the circuit. Additionally, the MPZ macro draws output current from the supplies' nodes instead of the ground node. This is useful when power supply requirements are evaluated. The real power of the MPZ macro, however, is in the ac domain. If an op amp has more than two poles and/or additional pole/zero pairs in its trans- fer function, the Boyle model is unable to do an adequate job simulating the op amp. V1 OPA27 RG R R Out R R OPA27 V2 VOUT = 2(1 + R/RG)(V1–V2) FIGURE 3. An Instrumentation Amplifier Using the Industry Standard OPA27. To demonstrate this, the application in Figure 3 was chosen. A test to determine the ac accuracy of an op amp macromodel that is frequently recommended is to compare the simulated unity-gain transient response of the op amp to the actual performance of the device at the bench. Although this is a good place to start when performing the macromodel ac performance verification, most macros are optimized to have the correct gain/phase at the zero crossing of the transfer function (see Figures 4 and 5). When the application demands that the op amp macromodel performs with various configurations, the real power of the MPZ macromodel topology is easily demonstrated. The OPA27, a generic amplifier, is used to demonstrate. 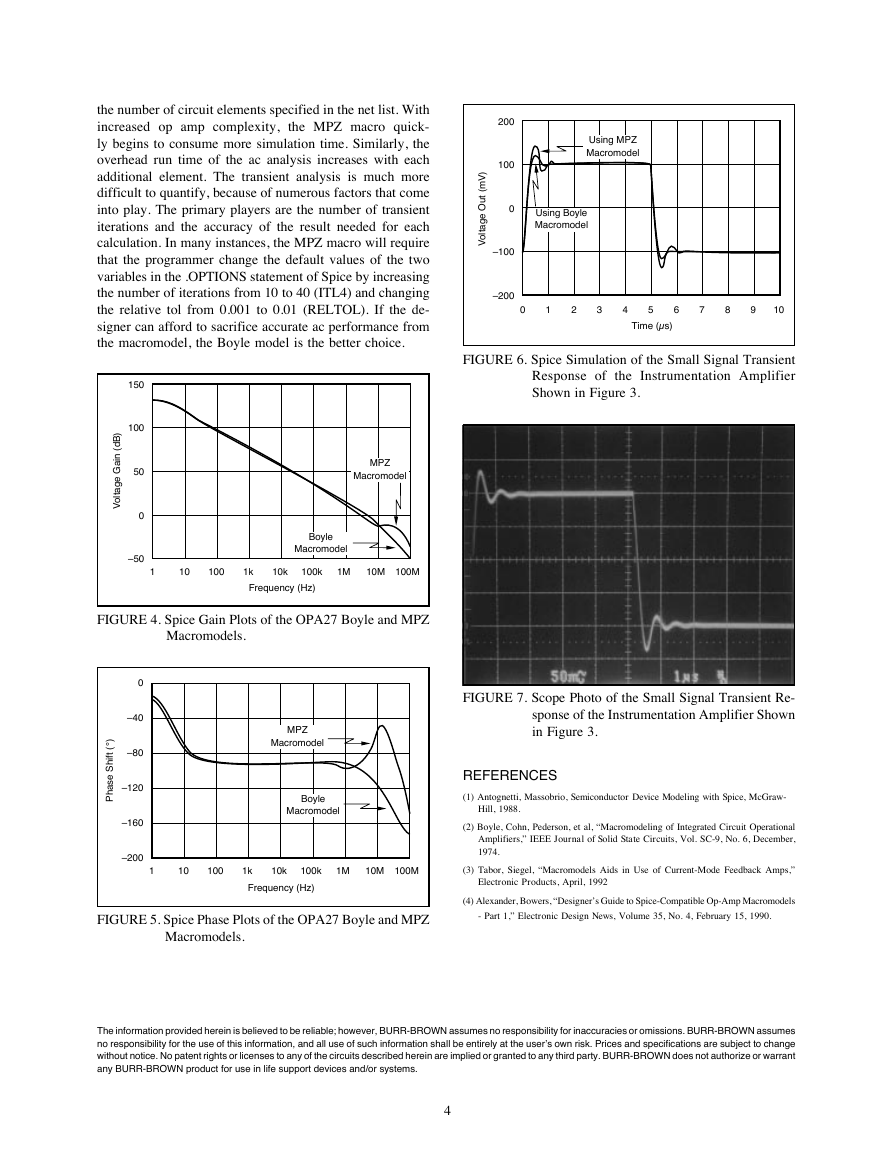The simulated results of Figure 3 are shown in Figure 6. In Figure 6, the excessive phase of the two op amp instrumentation amplifier is mod- elled successfully by the MPZ macro (19.2% overshoot) and unsuccessfully by the Boyle model (9.3% overshoot). The scope photo in Figure 7 verifies the MPZ as being the more accurate macro for this application. On the other hand, the Boyle macro outperforms the MPZ macro in better simula- tion time and use of computer memory. When simulating one op amp, this is not a critical issue: however, in multiple amplifier applications the MPZ macro becomes CPU hun- gry. Assuming no convergence problems exist in the mac- ros, the operating-point calculation is largely a function of 3 

) V m ( t u O e g a t l o V Using MPZ Macromodel Using Boyle Macromodel 200 100 0 –100 –200 0 1 2 3 4 5 6 7 8 9 10 Time (µs) FIGURE 6. Spice Simulation of the Small Signal Transient Response of the Instrumentation Amplifier Shown in Figure 3. the number of circuit elements specified in the net list. With increased op amp complexity, the MPZ macro quick- ly begins to consume more simulation time. Similarly, the overhead run time of the ac analysis increases with each additional element. The transient analysis is much more difficult to quantify, because of numerous factors that come into play. The primary players are the number of transient iterations and the accuracy of the result needed for each calculation. In many instances, the MPZ macro will require that the programmer change the default values of the two variables in the .OPTIONS statement of Spice by increasing the number of iterations from 10 to 40 (ITL4) and changing the relative tol from 0.001 to 0.01 (RELTOL). If the de- signer can afford to sacrifice accurate ac performance from the macromodel, the Boyle model is the better choice. ) B d ( i n a G e g a t l o V 150 100 50 0 –50 MPZ Macromodel Boyle Macromodel 1 10 100 1k 10k 100k 1M 10M 100M Frequency (Hz) FIGURE 4. Spice Gain Plots of the OPA27 Boyle and MPZ Macromodels. ) ° ( t f i h S e s a h P 0 –40 –80 –120 –160 –200 MPZ Macromodel Boyle Macromodel FIGURE 7. Scope Photo of the Small Signal Transient Re- sponse of the Instrumentation Amplifier Shown in Figure 3. REFERENCES (1) Antognetti, Massobrio, Semiconductor Device Modeling with Spice, McGraw- Hill, 1988. (2) Boyle, Cohn, Pederson, et al, “Macromodeling of Integrated Circuit Operational Amplifiers,” IEEE Journal of Solid State Circuits, Vol. SC-9, No. 6, December, 1974. 1 10 100 1k 10k 100k 1M 10M 100M (3) Tabor, Siegel, “Macromodels Aids in Use of Current-Mode Feedback Amps,” Frequency (Hz) Electronic Products, April, 1992 FIGURE 5. Spice Phase Plots of the OPA27 Boyle and MPZ Macromodels. (4) Alexander, Bowers, “Designer’s Guide to Spice-Compatible Op-Amp Macromodels - Part 1,” Electronic Design News, Volume 35, No. 4, February 15, 1990. The information provided herein is believed to be reliable; however, BURR-BROWN assumes no responsibility for inaccuracies or omissions. BURR-BROWN assumes no responsibility for the use of this information, and all use of such information shall be entirely at the user’s own risk. Prices and specifications are subject to change without notice. No patent rights or licenses to any of the circuits described herein are implied or granted to any third party. BURR-BROWN does not authorize or warrant any BURR-BROWN product for use in life support devices and/or systems. 4 

IMPORTANT NOTICE Texas Instruments and its subsidiaries (TI) reserve the right to make changes to their products or to discontinue any product or service without notice, and advise customers to obtain the latest version of relevant information to verify, before placing orders, that information being relied on is current and complete. All products are sold subject to the terms and conditions of sale supplied at the time of order acknowledgment, including those pertaining to warranty, patent infringement, and limitation of liability. TI warrants performance of its semiconductor products to the specifications applicable at the time of sale in accordance with TI’s standard warranty. Testing and other quality control techniques are utilized to the extent TI deems necessary to support this warranty. Specific testing of all parameters of each device is not necessarily performed, except those mandated by government requirements. Customers are responsible for their applications using TI components. In order to minimize risks associated with the customer’s applications, adequate design and operating safeguards must be provided by the customer to minimize inherent or procedural hazards. TI assumes no liability for applications assistance or customer product design. TI does not warrant or represent that any license, either express or implied, is granted under any patent right, copyright, mask work right, or other intellectual property right of TI covering or relating to any combination, machine, or process in which such semiconductor products or services might be or are used. TI’s publication of information regarding any third party’s products or services does not constitute TI’s approval, warranty or endorsement thereof. Copyright  2000, Texas Instruments Incorporated