论文研究-一种估计LFM信号参数的快速算法及其推广 .pdf-资料库

中国科技论文在线 http://www.paper.edu.cn 一种估计 LFM 信号参数的快速算法及其推广1 王勇，姜义成哈尔滨工业大学电子工程技术研究所，哈尔滨（150001） E-mail：wangyong6012@hit.edu.cn 摘要：提出一种估计线性调频(LFM)信号参数的快速算法，该算法利用计算信号的 WVD(wigner-ville distribution)得到其时间－频率值的二维分布，进而通过计算不同的时间采样点所对应的频率值来获取 LFM 信号的调频斜率以及初始频率的估计。算法的实现只需进行一维搜索，计算量小。分析该算法的统计特性，得到 LFM 信号参数估值均方误差的理论表达式。同时，对该算法进行推广，推广后的算法可用来估计多项式相位信号的参数。最后，通过计算机仿真实验验证算法的有效性。关键词：LFM 信号；WVD；统计特性；多项式相位信号 0 引言线性调频(linear frequency modulated, LFM)信号在雷达、声纳以及生物工程等领域有着极其广泛的应用，其中，初始频率和调频率作为表征线性调频信号特性的基本参数，其估计问题一直是信号处理的重要研究内容[1]。长期以来，各种基于最大似然估计(ML)的算法是解决这一问题的主要途径，这些算法可归结为多变量的最优化问题，其对 LFM 信号参数的估计精度取决于搜索过程中所采用的步长大小，计算量非常大[2-3]。线性调频信号在时频域内的聚焦特性提供了参数估计的时频方法，如 Radon-Wigner 变换(RWT)[4-5]、Radon Ambiguity 变换(RAT)[6]、分数阶傅里叶变换(FRFT)[7]等。这些算法的运算量与 ML 相比有较大减少，但仍然需要繁琐的搜索和计算。因此，如何快速、精确地估计 LFM 信号的参数仍是目前亟待解决的问题。在这种情况下，本文提出了一种估计 LFM 信号参数的快速算法，该算法通过计算信号的 WVD，得到其时间－频率值的二维分布，进而通过计算不同的时间采样点对应的频率值来获取 LFM 信号的调频斜率以及初始频率的估计。整个算法的实现只需进行一维搜索，实现起来非常容易。同时，本文基于扰动分析理论推导了该算法的统计特性，得到了 LFM 信号参数估值均方误差的理论表达式。最后，本文对该算法进行了推广，推广后的算法可用来估计多项式相位信号的参数。计算机仿真结果验证了本文算法的有效性。 1 算法的提出本文中考虑如下形式的 LFM 信号： z n ( ) = s n ( ) + v n ( ) = b 0 e j a ( 0 + a n a n 1 2 + 2 ) + v n ( ) ≤， n N 1 − 2 。 (1) 式中： )(nv 是均值为 0，方差为 2σ 的高斯白噪声；为信号长度，假定信号的采样率为 1。 baaa ,{ }, 0 0 , 2 1 为需要估计的参数； N 最初的参数估计方法是基于最大似然(ML)原理，利用多维搜索获得参数的估计，整个实现过程如下： ( ˆ ˆ a a , 1 2 ) = arg max ( a a , 1 2 ) 1本课题得到高等学校博士学科点专项科研基金(20060213009)的资助。 -1- ( N 1) 2 − ∑ n =− ( N 1) 2 − z n ( )e − j a n a n ( 2 + 1 2 ) ， (2)

中国科技论文在线 http://www.paper.edu.cn ( N 1) 2 − ∑ ( N 1) 2 − ˆ b 0 = 1 N ˆ a 0 = angle n =− ⎧ ⎨ ⎩ n z n ( )e − j a n a n ( 2 ˆ 1 + ˆ 2 ) ， (3) ( N 1) 2 − ∑ ( N =− 1) 2 − z n ( )e − j a n a n ( 2 ˆ 1 + ˆ 2 ) ⎫ 。 (4) ⎬ ⎭ NO ( 2 log N ) 由式(2)可以看出，ML 算法需要进行二维搜索，计算量为，这在很大程度上限制了它的工程应用。为此，借助于 LFM 信号在时频域内的聚焦特性，一些基于时频分析的参数估计算法相继提了出来。其中，最为典型的是基于 Radon-Wigner 变换(RWT)的方法。众所周知，对于 LFM 信号来说，它的 Wigner 分布是位于其瞬时频率位置上的一个冲击函数，因而具有理想的信号聚集度。而 Radon 变换是图像处理中一种检测与估计平面上的直线的方法，与 Wigner 分布相结合，即可估计出 LFM 信号的调频斜率与初始频率。其中，Wigner 分布的计算可通过快速傅里叶变换来实现，比较简单；而 Radon 变换则是一种线性积分过程，同时，在参数估计时需不断旋转坐标轴的角度，这在很大程度上增加了算法的计算量。为此，本文做如下考虑：计算出 LFM 信号的 Wigner 分布后，即可得到其时间－频率值的二维分布，此时，通过计算 2 个不同时间采样点所对应的频率值即可获得 LFM 信号的调频斜率与初始频率估计。这个过程只需要一维搜索，避免了 Radon 变换的线性积分过程以及坐标轴角度的旋转，极大地减小了计算量。算法的实现步骤如下：对于如式(1)所示的 LFM 信号 )(ns ，其离散形式(WVD)可定义为 ( N 1) 2 − ( N 1) 2 − ∗ 0 = m ( ) 2 − jum − + = )e ∑ n u WVD( , ) s n m s n m ( ∑ m 0 = nu 由上式可见，LFM 信号 )(ns 的 WVD 集中在直线上，定义为 )(ns 的 )( 瞬时频率。此时，通过计算不同时间采样点所对应的频率值即可获得 1a 和 2a 的估计，方法如下：。 (5) na 2 a n u m 2 b 2 0 j a 2 ( 1 a 1 + = = 2 e + − 2 ) 1) 分别计算 1n 和 2n 时刻的瞬时频率值 ˆ a n 2 2 ˆ a n 2 2 ˆ u n ( ) 1 ˆ u n ( ) 2 ˆ a 1 ˆ a 1 + + = = ) ) 和 ( 2nu ，可以得到 ( 1nu ， (6) 1 。 (7) 2 2) 由以上两式可以获得 1a 和 2a 的估计为 ˆ u n n ( ) − 2 n − 2 ˆ u n ( − 2 n ) − 2 ˆ u n n ) ( 1 n 1 ˆ u n ( ) 1 n 2( 1 ˆ a 1 ˆ a = = ) 2 1 2 ， (8) 。 (9) 3) 估计出 1a 和 2a 后，即可由式(3)、(4)获得 0a 和 0b 的估计。在以上算法中，时间采样点 1n 和 2n 的选取在一定程度上会影响参数 1a 和 2a 估值的均方时，参数 1a 估值的均方误差达到最小，具体分析过程将在误差。理论分析表明，当第 3 节中给出； 2n 的选取对参数 2a 估值的影响不大，大量仿真实验表明，可取 n ，此时 2a 估值的均方误差基本不变。以上即是本文提出的 LFM 信号参数估计算法，为了衡量该算法的参数估计性能，需了解其统计特性，下面，本文采用扰动分析[8]的原理来进行推导。 N 1.0 1 =n 3.0 → N = 0 2 -2-

中国科技论文在线 2 统计特性分析 http://www.paper.edu.cn 在噪声的影响下，信号 )(nz 的 WVD 可分为信号函数与噪声函数 2 部分，分别为 ( N g u ( ) = 1) 2 − ∑ m = 0 − n s n m s n m ( − + ) ( ∗ − 2 )e jum ， (10) δ g u ( ) 其中 ( N 1) 2 − = ∑ m = 0 − n z n m sv ( , )e 2 − jum 。 (11) ) z n m s n m v n m s n m v n m v n m v n m sv( , ( 此时，根据扰动分析理论，可以得到扰动量 uδ 的数学表达式 ) ( = + − + − + + + ) ( ) ) ( ( ) ( ∗ ∗ ∗ − 。 ) u δ ≈ − Re Re δ ∂ g u ( ) 0 2 ∂ g u ( ) 0 ) 0 + ) + 0 g u ( ∗ u ∂ g u ( ∗ u 2 ∂ g u ( ∂ u ∂ g u ( ∂ u ∂ 0 ⎧ ⎨ ⎩ ⎧ ⎨ ⎩ ) 0 δ g u ( ∗ 0 ) ) ) 0 g u ( ∗ ∂ u ∂ ⎫ ⎬ ⎭ ⎫ ⎬ ⎭ ， (12) 式中， 0u 为信号 )(ns 的瞬时频率。将式(10)、(11)代入到式(12)中，并经过化简，可以得到如下结果： u E u { δ δ 1 ⋅ 2 } ≈ ) Im( 36 {Im( η η ⋅ 2 1 n N 2 ( ) ( 3 − 1 E 2 − b N 4 0 )} n 2 3 ) ， (13) 其中 η i 式中， 2,1=i ≈ ( N 1) 2 − ∑ m 。 = 0 − n i ( m N − ( 2 − n i ) 2) z n m * sv ( , )e 2 ju m i ， (14) = n 经过化简，可以得到，当 n 1 24 SNR 3 式中，SNR 为输入信噪比，定义为 E a { δ ≈ 1 N } 2 2SNR 2 0 SNR b σ= 2 。 = 0 2 (1 + 时，参数 1a 估值的均方误差达到最小，为 1 ) ， (15) 令 n 2 = N 1.0 ，可以得到参数 2a 估值的均方误差近似为 E a { δ 2 2 } ≈ 500 SNR 5 N (4 + 1 SNR ) 。 (16) 比较式(15)、(16)与 1ˆa 和 2ˆa 的 Cramer-Rao 下界[9]，可以看出，当 N 充分大时，所得 LFM 信号参数估计 1ˆa ， 2ˆa 的均方误差与相应的 Cramer-Rao 下界关于 N 的收敛性具有相同的数量级。 3 算法的推广形式本文第 2 节提出了基于 WVD 的 LFM 信号参数估计算法，该算法是根据 LFM 信号的 WVD 集中在其瞬时频率上，即 WVD 对于 LFM 信号瞬时频率的估计是无偏的，来进行参数估计的。在实际应用中，除了 LFM 信号外，更为普遍的则是非线性调频信号，由于其相位是关于时间的多项式函数，故又称之为多项式相位信号。如雷达接收机接收到的信号中相 -3-

中国科技论文在线 http://www.paper.edu.cn 位的高次项反映目标相对于雷达的运动特性，等等。因此，多项式相位信号的参数估计一直是人们普遍感兴趣的一个问题。目前最为流行的方法是基于高阶模糊度函数及其改进形式的方法[10-11]，但此类方法是依次估计出多项式相位系数，存在误差传递效应。本节研究在多项式相位信号情况下，如何应用信号的 WVD 或其改进形式来进行参数估计。对于最高相位次数超过二次的多项式相位信号，其 WVD 对瞬时频率的估计是有偏的，因此，需对 WVD 的形式做一些改进，使之能够应用第 2 节估计 LFM 信号的原理来进行参数估计。首先，考虑如下形式的多项式相位信号： z n ( ) = s n ( ) + v n ( ) = j b 0 e M ∑ m = 0 m a n m + v n n ( ), ≤ N 1 − 2 ， (17) 式中： mmab = 为待估计参数； )(nv 是均值为 0，方差为 2σ 的高斯白噪声； N 为信号 } ,{ M 0 0 的特点，有长度，采样率为 1。下面，分析此时信号 )(ns 的 WVD 核函数 knskns ( − + ) ( ) ∗ M ∑ m = 0 j ) = b 2 0 e a m [( n k + ) m n k ( − − ) m ] = s n k s n k ( − + ) ∗ ( m ⎞ ⎟ i ⎠ M m ∑∑ m i 0 = = 0 ⎛ ⎜ ⎝ i m i − n k a m [1 ( 1) − − m i − ] j j j j b 2 0 e b 2 0 e b 2 0 e b 2 0 e M M ∑∑ i = 0 m i = m i ⎞ ⎟ ⎠ ⎛ ⎜ ⎝ i m i − n k a m [1 ( 1) − − m i − ] M M i − ∑∑ i = 0 l = 0 i l +⎛ ⎜ i ⎝ ⎞ ⎟ ⎠ i l n k a l + i l [1 ( 1) ] − − = M ∑ l = 0 l c k l ， = = (18) 其中 c l = M l − ∑ i = 0 l +⎛ ⎜ i ⎝ i ⎞ ⎟ ⎠ n a i l + i [1 ( 1) ] l − − 。 (19) 由式 (19) 可见， c l 2 =′ ，这里 int(⋅ 表示取整运算；而 ) , )) l (0 ,1,0 int( =′ M 2 1= ，其中 M 2 2 +′lc ，进而估计出参数 M mma ) 1][1 ( 1) − M 2 + − int( + ] M c l 2 l (1 +′ =′ ,1,0 , L ) mma 中包含了所有参数 M L = {[int( )[1 ( 1) − − M ]} 2 。因此，需首先估计出参数 1 在 WVD 的基础上，定义如下变换： 1= ，这可由以下方法来实现。 ( W n c ( ; 2 l 1 ′+ ) = 其中 N 1) 2 − ∑ k = 0 s n k s n k ( − + ) ( ∗ − jH k ( )e ) ， (20) L H k ( ) l 1 ′+ c 2 = ∑ l ′= L ) 的估计可由如下最优准则来实现： 0 k ′+ l 1 2 。 (21) 此时，系数 c l 2 l (1 +′ =′ ,1,0 , -4-

中国科技论文在线 ˆ c 2 l ′ 1 + = http://www.paper.edu.cn W n c ( ; 2 l ′ 1 + ) 。 (22) mma 中估计出参数 M 2 +′lcnW 1 )5.0 处的 ;( 1= ，此时，只需分别计算出 2 ) 即可。为证明此结论，下面 arg max l 1 ′+ c 2 ,1,0 0( =′ Nx ) L , x << l (1 +′ n 2 = 下面研究如何从系数 c l 2 个时间采样点 1 =n 0 和分 2 种情况进行分析： 1） M 为偶数 ˆ c 。由于 1 =n 0 ˆ, −Ma 1 ，由式 (22) 可以估计出 + 1 − 1 ˆ, a 令 ,ˆ,ˆ aa 1 3 1 − 到 Maˆ 的估计，由估计出的 mma 以获得参数 M 1= 的估计。 2） M 为奇数 ˆ(2 a ˆ, a = ˆ a M M M M − ,ˆ,ˆ cc 3 1 ˆ naM ) M ˆ, −Mc 1 ，进而由式 (19) 可以估计出系数 n Nx ，此时再令 ˆ −Mc 即可得到 2 = ，即可得 ˆ −Ma 的估计，依次类推，可 << )5.0 0( x 2 M − 3 以及 3 2 2 − M ˆ c = + Nx ˆ, Mc ，由式 (22) 可以估计出令 ,ˆ,ˆ 1 。由于 aa 3 n )5.0 = 1 =n 0 ˆ, Ma 0( << ˆ −Ma 的估计，依次类推，可以获得参数 M mma ˆ[2 a M ˆ −Ma 的估计，由估计出的 ,ˆ,ˆ 1 ，进而由式 (19) 可以估计出系数 cc 3 M ( − ，此时再令 ˆ −Mc 以及 4 即可得到 3 而参数 0a 和 0b 的估计可通过对原信号解调频来实现，类似于式(3)和式(4)。以上即是本文提出的估计多项式相位信号参数的算法。这里，有如下几点需要说明： − ˆ, a M 1= 的估计。，即可得到 1 na M ˆ, a MMn ]2 ˆ, a ˆ)1 a ˆ)1 ( ˆ a + x 1 − 1 − M M M M − − − 4 2 2 2 1) 由式(22)可以看到，系数 c l 2 l (1 +′ =′ ,1,0 , L ) 的估计也是一个多维搜索过程，多项式相位信号的最高阶次每增加 2 次，搜索过程便增加一维，这会导致计算量的增加。因此，本文算法更适用于阶次不高的情形。当信号最高阶次不超过 4 次时，该算法只需进行二维搜索。 1 =n 2) 当 ˆ, Ma 不存在相互依赖的关系，这在一定程度上减轻了多参数估计过程中的误差传递效应。时，由式(22)和式(19)所估计出的系数 ,ˆ,ˆ aa 1 3 ,ˆ,ˆ 1 之间 aa 3 ˆ, −Ma 1 或 0 mma 3) 该算法具有较好的参数估计性能，采用扰动分析原理可以获得参数 M 1= 估值的均方误差表达式(具体推导过程从略)如下(以 4=M n 2 = N 1.0 )：为例，其中取 1 ) ， E a { δ 1 2 } ≈ E a { δ 2 2 } ≈ E a { δ 3 2 } ≈ E a { δ 4 2 } ≈ ⎧ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎩ (1 (1 150 N SNR 3 13000 N SNR 5 22400 N SNR 9 100000 (1 N SNR 7 9 ) ， + + 2SNR 1 2SNR 1 (1 + 2SNR 1 ) 。 2SNR + . (23) ) ， 4) 由式(19)可以得到 c 1 = 2 M ∑ i 1 = i 1 − ia n i = 2IF[ ( )] s n ， (24) -5-

中国科技论文在线 http://www.paper.edu.cn 其中，IF[ ]⋅ 代表信号的瞬时频率。因此，该算法在估计多项式相位信号参数的同时，还可以获得信号瞬时频率的估计。 5) 由式(20)可以看出，估计出系数 c l 2 l (1 +′ =′ ,1,0 , L ) 后，由 1cnW ;( ) 所构造的时频分布对于多项式相位信号而言，具有理想的频率聚集性，消除了高次项所产生的自交叉项影响，克服了传统 WVD 对于非线性调频信号的频率聚集性较差的缺点。 4 仿真实验为验证本文所提算法的有效性以及误差分析的结果，本节给出了相应的 Monte-Carlo 仿真实验结果。分别针对 LFM 信号以及四次相位信号的情况，整个实验包括 2 部分： 1) LFM 信号参数估计 LFM 信号的样本长度为 255，各参数为： 0 =b 1 ， 0 =a 1 a = ， 1 π 8 ， 2 =a 005.0 。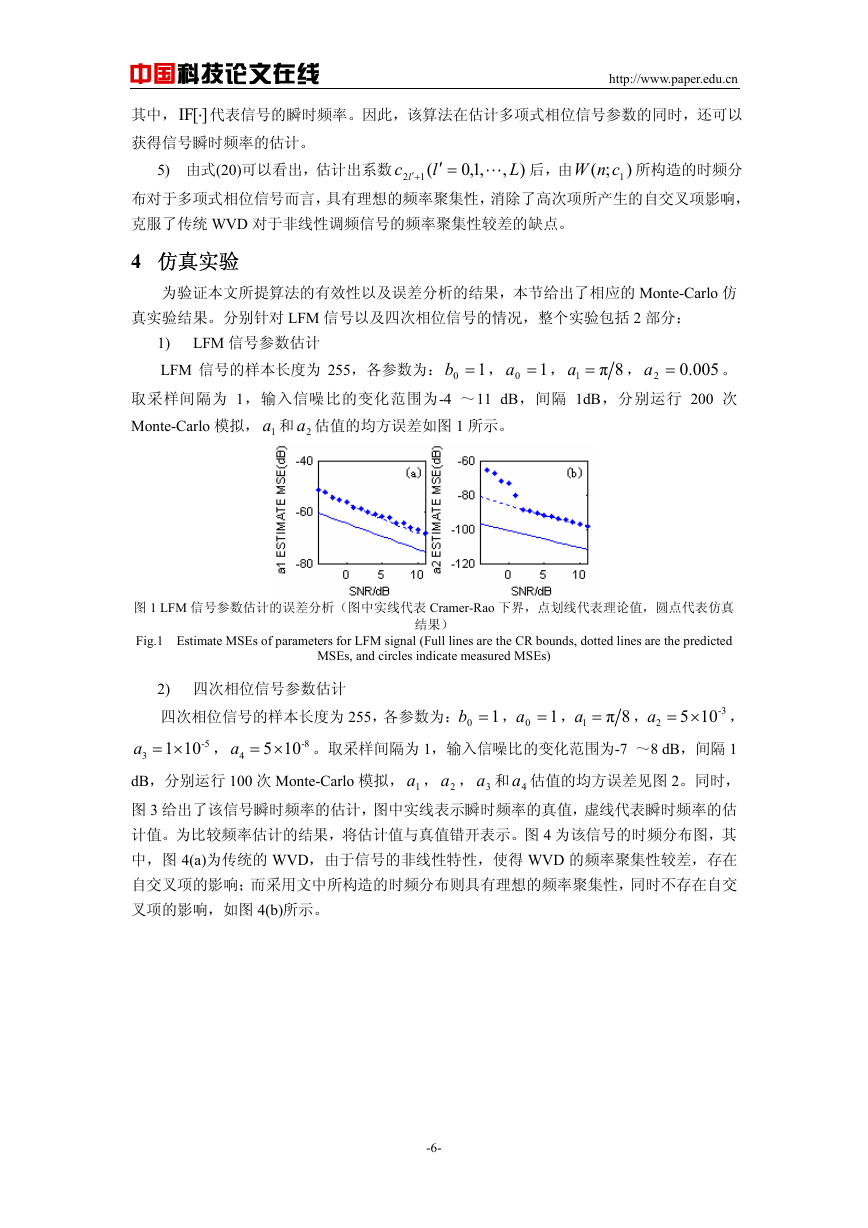取采样间隔为 1，输入信噪比的变化范围为-4 ～11 dB，间隔 1dB，分别运行 200 次 Monte-Carlo 模拟， 1a 和 2a 估值的均方误差如图 1 所示。图 1 LFM 信号参数估计的误差分析（图中实线代表 Cramer-Rao 下界，点划线代表理论值，圆点代表仿真 Fig.1 Estimate MSEs of parameters for LFM signal (Full lines are the CR bounds, dotted lines are the predicted MSEs, and circles indicate measured MSEs) 2) 四次相位信号参数估计四次相位信号的样本长度为 255，各参数为：， -3 -5 -8 π 8 ， 0 =b 1 1 a = ， 1 0 =a 5 10 5 10 a = × ， 2 a = × 。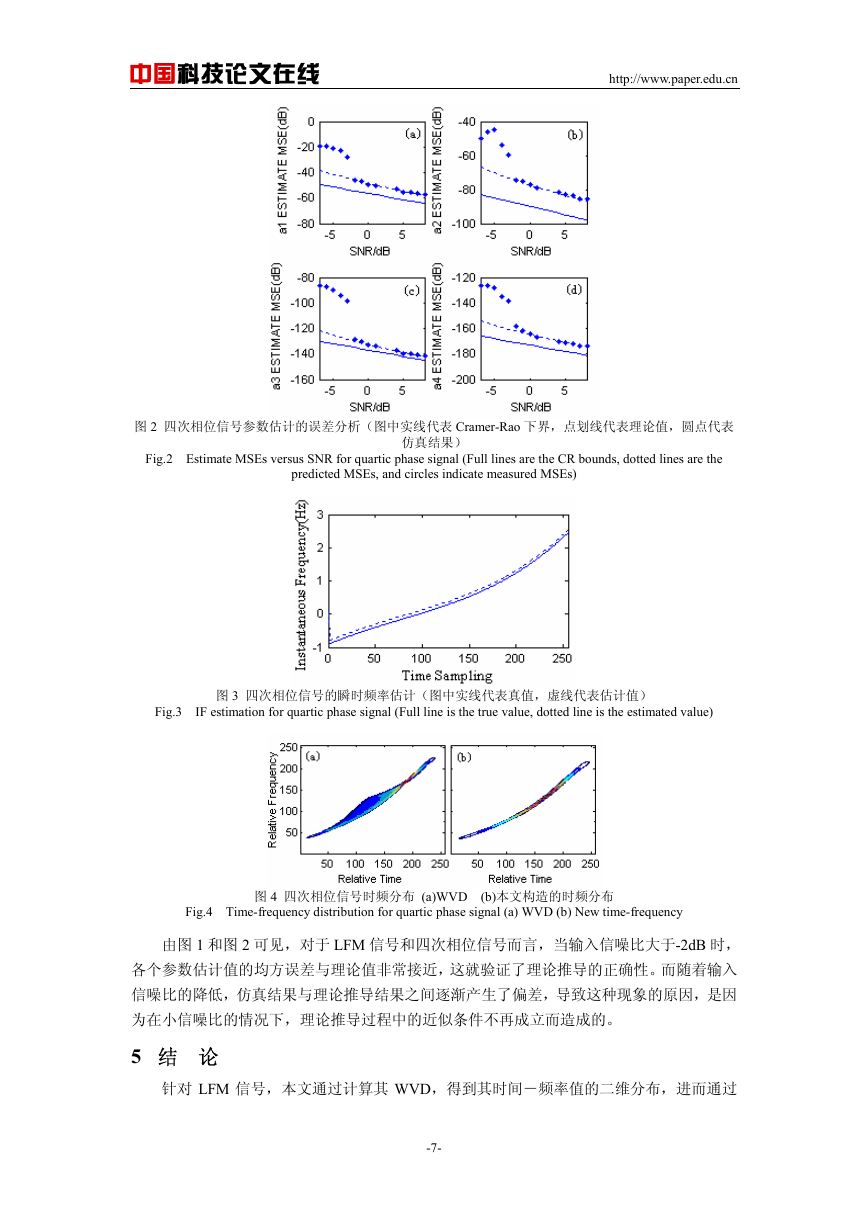取采样间隔为 1，输入信噪比的变化范围为-7 ～8 dB，间隔 1 a = × ， 3 1 10 4 dB，分别运行 100 次 Monte-Carlo 模拟， 1a ， 2a ， 3a 和 4a 估值的均方误差见图 2。同时，图 3 给出了该信号瞬时频率的估计，图中实线表示瞬时频率的真值，虚线代表瞬时频率的估计值。为比较频率估计的结果，将估计值与真值错开表示。图 4 为该信号的时频分布图，其中，图 4(a)为传统的 WVD，由于信号的非线性特性，使得 WVD 的频率聚集性较差，存在自交叉项的影响；而采用文中所构造的时频分布则具有理想的频率聚集性，同时不存在自交叉项的影响，如图 4(b)所示。结果） -6-

中国科技论文在线 http://www.paper.edu.cn 图 2 四次相位信号参数估计的误差分析（图中实线代表 Cramer-Rao 下界，点划线代表理论值，圆点代表 Fig.2 Estimate MSEs versus SNR for quartic phase signal (Full lines are the CR bounds, dotted lines are the predicted MSEs, and circles indicate measured MSEs) 仿真结果）图 3 四次相位信号的瞬时频率估计（图中实线代表真值，虚线代表估计值） Fig.3 IF estimation for quartic phase signal (Full line is the true value, dotted line is the estimated value) 图 4 四次相位信号时频分布 (a)WVD (b)本文构造的时频分布 Fig.4 Time-frequency distribution for quartic phase signal (a) WVD (b) New time-frequency 由图 1 和图 2 可见，对于 LFM 信号和四次相位信号而言，当输入信噪比大于-2dB 时，各个参数估计值的均方误差与理论值非常接近，这就验证了理论推导的正确性。而随着输入信噪比的降低，仿真结果与理论推导结果之间逐渐产生了偏差，导致这种现象的原因，是因为在小信噪比的情况下，理论推导过程中的近似条件不再成立而造成的。 5 结论针对 LFM 信号，本文通过计算其 WVD，得到其时间－频率值的二维分布，进而通过 -7-

中国科技论文在线 http://www.paper.edu.cn 计算不同的时间采样点对应的频率值来获取 LFM 信号的参数估计。同时，文中对该方法进行了推广，通过定义新的变换实现多项式相位信号的参数估计。基于扰动分析理论得到了该算法的统计特性，进而通过计算机仿真实验验证了该算法的有效性。参考文献 [1] O’shea Peter. A fast algorithm for estimating the parameters of a quadratic FM signal[J]. IEEE Transactions on Signal Processing, 2004, 52(2): 385-393. [2] Abatzoglou T. Fast maximum likelihood joint estimation of frequency and frequency rate[J]. IEEE Transactions on Aerospace and Electronic Systems, 1986, 22(6): 708-715. [3] Liang R M, Arun K S. Parameter estimation for superimposed chirp signals[C]//Acoustics, Speech, and Signal Processing. San Francisco, CA, USA, 1992, 5: 273-276. [4] Raveh I, Mendlovic D. New properties of the Radon transform of the cross wigner/ambiguity distribution function[J]. IEEE Transactions on Signal Processing, 1999, 47(7): 2077-2080. [5] Barbarossa S. Analysis of multicomponent LFM signals by a combined Wigner-Hough transform[J]. IEEE Transactions on Signal Processing, 1995, 43(6): 1511-1515. [6] Wang M S, Chan A K, Chui C K. Linear frequency modulated signal detecting using radon-ambiguity transform[J]. IEEE Transactions on Signal Processing, 1998, 46(3): 571-586. [7] Qi Lin, Tao Ran, Zhou Siyong, et al. Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J]. Science in China Series F: Information Sciences, 2004, 47(2): 184-198. [8] Peleg S, Porat B. Linear FM signal parameter estimation from discrete-time observations[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(4): 607-616. [9] Peleg S, Porat B. The Cramer-Rao lower bounds for signals with constant amplitude and polynomial phase[J]. IEEE Transactions on Signal Processing, 1991, 39(5): 749-752. [10] Barbarossa S, Petrone V. Analysis of polynomial-phase signals by the integrated generalized ambiguity function[J]. IEEE Transactions on Signal Processing, 1997, 45(2): 316-327. [11] Barbarossa S, Scaglione A, Giannakis G B. Product hige-order ambiguity function for multicomponent polynomial-phase signal modeling[J]. IEEE Transactions on Signal Processing, 1998, 46(3): 691-708. A fast algorithm for estimating the parameters of a LFM signal and its extension Research Institute of Electronic Engineering Technology, Harbin Institute of Technology, Harbin, Wang Yong, Jiang Yicheng China (150001) Abstract A fast algorithm for estimating the parameters of a LFM signal is presented in this paper. This algorithm is based on the fact that the WVD of a LFM signal concentrates along the instantaneous frequency, and can be implemented by estimating the frequencies at different time positions, hence, the chirp rate and the initial frequency can be obtained. The proposed algorithm is fast in that it requires only one-dimensional maximizations. The statistical performance of this algorithm is analyzed, and the theoretical expressions of the mean square error (MSE) of the parameters are obtained. Then the algorithm is extended to estimate the parameters of a polynomial phase signal. The computer simulation results demonstrate the validity of the algorithm proposed. Keywords: LFM signal; WVD; statistical performance; polynomial phase signal 作者简介：王勇(1979—)，男，讲师，E-mail：wangyong6012@hit.edu.cn. -8-

资料库

论文研究-一种估计LFM信号参数的快速算法及其推广 .pdf

相关推荐

开发技术

热门标签

最新资料