第1页 / 共88页
第2页 / 共88页
第3页 / 共88页
第4页 / 共88页
第5页 / 共88页
第6页 / 共88页
第7页 / 共88页
第8页 / 共88页
《信号与系统》考研复习通用总结.pdf
1 序言
1.1 简介
1.2 版权
2 公共基础知识
2.1 不定积分
2.2 定积分
2.3 Gama函数
2.4 级数
2.5 排列组合
2.6 三角函数
3 电容电感的压流关系
3.1 电容
3.2 电感
3.3 RLC电路微分方程
4 傅氏拉氏Z变换部分分式展开
4.1 二阶
4.2 三阶（常规）
4.3 几个特殊变换对
4.3.1 Z变换
4.3.2 拉氏变换
4.4 三阶（特殊）
4.4.1 Z变换
4.4.2 拉氏变换
5 简答题
5.1 周期信号
5.2 非周期连续时间信号由来
5.3 线性时不变（LTI）系统
5.4 任意系统与LTI系统性质
5.4.1 因果性
5.4.2 稳定性
5.4.3 时不变性
5.4.4 线性
5.4.5 记忆和无记忆系统
5.4.6 可逆性与可逆系统
5.5 傅氏分析与变换
5.6 Fourier变换成立条件
5.6.1 连续时间周期信号
5.6.2 连续时间非周期信号傅氏变换存在的条件
5.7 采样定理
6 证明题
6.1 奇异函数的性质
6.1.1 脉冲函数时间收缩性
6.1.2 冲激信号的导数
6.2 奇异函数与卷积
6.3.2 例2
6.3.3 例3
6.3.4 例4
6.4 Laplace变换
7 计算题
7.1 FT与LT存在性
7.2 ZT与DTFT存在性
7.3 拉氏反变换ILT
7.4 [变换]综合应用
7.4.1 符号函数与相移系统
7.4.2 信号流图
7.4.3 FT计算
7.4.4 LT计算
7.4.5 DTFT计算
7.5 方波时域卷积
7.6 采样定理
8 零极点图与系统性质
8.1 连续时间系统
8.1.1 零极点定义
8.1.2 例1
8.1.3 例2
8.1.4 例3
8.1.5 例4
8.1.6 因果稳定性与零极点图
8.2 离散时间系统
8.2.1 零极点定义
8.2.2 例1
8.2.3 例2
8.2.4 例3
8.2.5 例4
8.2.6 因果稳定性与零极点图
9 系统框图专项问题
9.1 典型框图总结
9.1.1 基本框图
9.1.2 高阶框图
9.1.2.1 连续时间信号
9.1.2.2 离散时间信号
9.2 框图例题
9.2.1 例1
9.2.2 例2
9.2.3 例3
10 作图题
10.1 例1
10.2 例2
10.3 例3
10.4 例4
11 傅氏级数专项
11.1 典型周期信号
11.1.1 周期方波1
11.1.2 周期方波2
11.1.3 周期脉冲串
11.2 例题
12 附录
12.1 LTI系统的运算性质
12.1.1 交换律
12.1.2 分配率
12.1.3 结合律
12.1.4 微积分性
12.1.5 线性时不变性
12.2 常用卷积公式
12.3 常见信号的FT,LT,ZT,DTFT
12.3.1 一般信号
12.3.2 奇异信号
12.3.3 指数信号
12.4 FT,LT,ZT,DTFT变换性质
12.4.1 时移性质
12.4.2 频移性质
12.4.3 时域尺度变换性质
12.4.4 时域微积分
12.4.5 时间反转
12.4.6 频复域微分性质
12.5 类Sinc函数的频谱
12.6 域正反变换总结
12.6.1 傅里叶级数（FS）
12.6.2 离散傅里叶变换（DFT）
12.6.3 傅里叶变换（FT）
12.6.4 Laplace变换
12.6.5 Z变换
12.7 英文简称及符号表示
12.7.1 英语简称
12.7.2 符号表示
《信号与系统》考研复习总结
目次
1 序言 .................................................................................................................................. 1
1.1 简介 ........................................................................................................................ 1
1.2 版权 ........................................................................................................................ 1
2 公共基础知识 ................................................................................................................... 2
2.1 不定积分 ................................................................................................................ 2
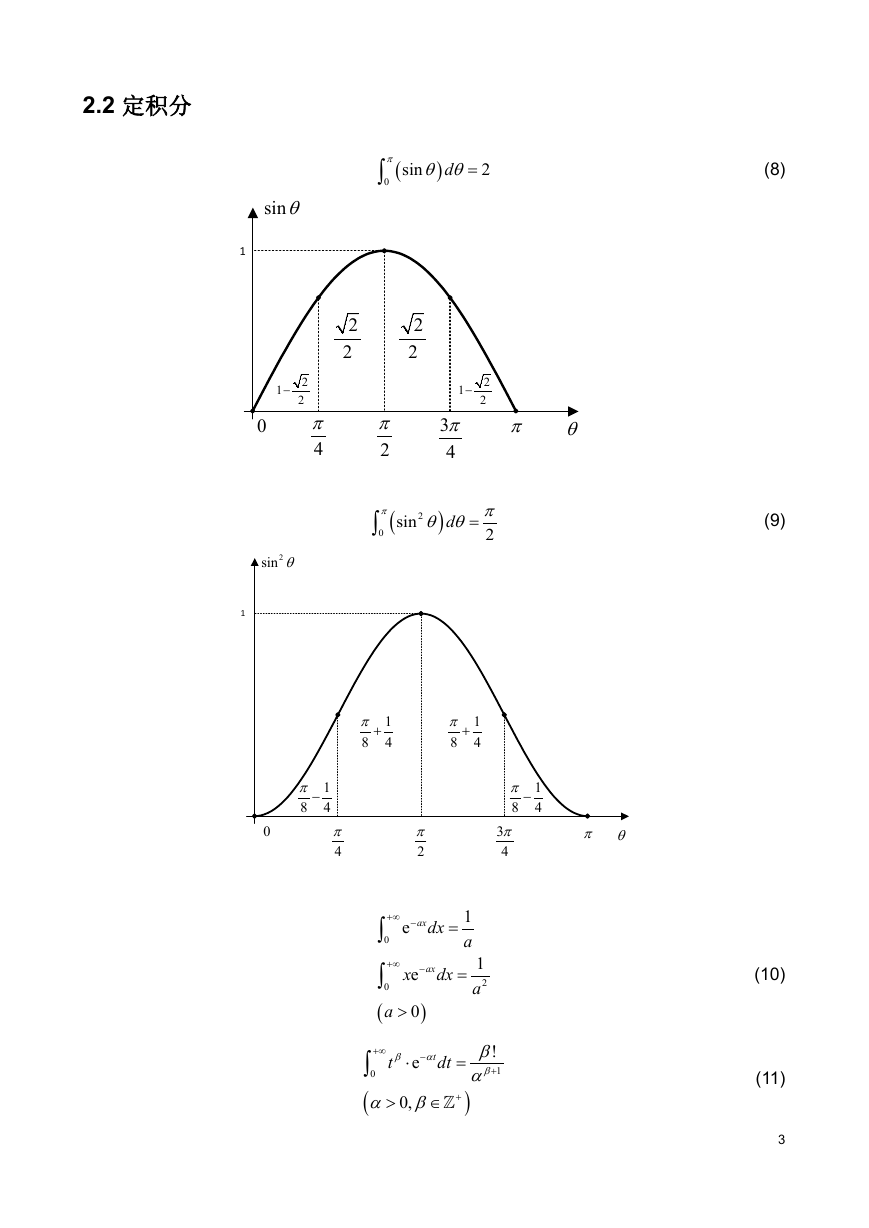
2.2 定积分 .................................................................................................................... 3
2.3 Gama 函数 .............................................................................................................. 4
2.4 级数 ........................................................................................................................ 4
2.5 排列组合 ................................................................................................................ 5
2.6 三角函数 ................................................................................................................ 5
3 电容电感的压流关系 ......................................................................................................... 8
3.1 电容 ........................................................................................................................ 8
3.2 电感 ........................................................................................................................ 8
3.3 RLC 电路微分方程 .................................................................................................. 9
4 傅氏拉氏 Z 变换部分分式展开 ........................................................................................ 10
4.1 二阶 ...................................................................................................................... 10
4.2 三阶（常规） ....................................................................................................... 10
4.3 几个特殊变换对 .................................................................................................... 11
4.3.1 Z 变换 ......................................................................................................... 11
4.3.2 拉氏变换 .................................................................................................... 11
4.4 三阶（特殊） ....................................................................................................... 12
4.4.1 Z 变换 ......................................................................................................... 12
4.4.2 拉氏变换 .................................................................................................... 12
5 简答题 ............................................................................................................................ 14
5.1 周期信号 .............................................................................................................. 14
5.2 非周期连续时间信号由来 ..................................................................................... 14
5.3 线性时不变（LTI）系统 ........................................................................................ 16
5.4 任意系统与 LTI 系统性质 ...................................................................................... 17
I
5.4.1 因果性 ........................................................................................................ 17
5.4.2 稳定性 ........................................................................................................ 18
5.4.3 时不变性 .................................................................................................... 18
5.4.4 线性 ........................................................................................................... 19
5.4.5 记忆和无记忆系统 ...................................................................................... 20
5.4.6 可逆性与可逆系统 ...................................................................................... 20
5.5 傅氏分析与变换 .................................................................................................... 20
5.6 Fourier 变换成立条件 ............................................................................................ 22
5.6.1 连续时间周期信号 ...................................................................................... 22
5.6.2 连续时间非周期信号傅氏变换存在的条件 .................................................. 23
5.7 采样定理 .............................................................................................................. 23
6 证明题 ............................................................................................................................ 25
6.1 奇异函数的性质 .................................................................................................... 25
6.1.1 脉冲函数时间收缩性 .................................................................................. 25
6.1.2 冲激信号的导数 .......................................................................................... 25
6.2 奇异函数与卷积 .................................................................................................... 26
6.3 傅里叶分析与变换 ................................................................................................ 28
6.3.1 例 1 ............................................................................................................ 28
6.3.2 例 2 ............................................................................................................ 29
6.3.3 例 3 ............................................................................................................ 29
6.3.4 例 4 ............................................................................................................ 30
6.4 Laplace 变换 ......................................................................................................... 30
7 计算题 ............................................................................................................................ 31
7.1 FT 与 LT 存在性 .................................................................................................... 31
7.2 ZT 与 DTFT 存在性 ............................................................................................... 32
7.3 拉氏反变换 ILT ..................................................................................................... 32
7.4 [变换]综合应用 ...................................................................................................... 33
7.4.1 符号函数与相移系统 .................................................................................. 33
7.4.2 信号流图 .................................................................................................... 35
7.4.3 FT 计算 ....................................................................................................... 37
II
7.4.4 LT 计算 ....................................................................................................... 40
7.4.5 DTFT 计算 .................................................................................................. 40
7.5 方波时域卷积 ....................................................................................................... 43
7.6 采样定理 .............................................................................................................. 43
8 零极点图与系统性质 ....................................................................................................... 45
8.1 连续时间系统 ....................................................................................................... 45
8.1.1 零极点定义 ................................................................................................. 45
8.1.2 例 1 ............................................................................................................ 45
8.1.3 例 2 ............................................................................................................ 46
8.1.4 例 3 ............................................................................................................ 47
8.1.5 例 4 ............................................................................................................ 48
8.1.6 因果稳定性与零极点图 ............................................................................... 49
8.2 离散时间系统 ....................................................................................................... 50
8.2.1 零极点定义 ................................................................................................. 50
8.2.2 例 1 ............................................................................................................ 50
8.2.3 例 2 ............................................................................................................ 51
8.2.4 例 3 ............................................................................................................ 52
8.2.5 例 4 ............................................................................................................ 53
8.2.6 因果稳定性与零极点图 ............................................................................... 54
9 系统框图专项问题 .......................................................................................................... 57
9.1 典型框图总结 ....................................................................................................... 57
9.1.1 基本框图 .................................................................................................... 57
9.1.2 高阶框图 .................................................................................................... 58
9.1.2.1 连续时间信号 ............................................................................................... 58
9.1.2.2 离散时间信号 ............................................................................................... 59
9.2 框图例题 .............................................................................................................. 60
9.2.1 例 1 ............................................................................................................ 60
9.2.2 例 2 ............................................................................................................ 61
9.2.3 例 3 ............................................................................................................ 63
10 作图题 .......................................................................................................................... 64
III
10.1 例 1 .................................................................................................................... 64
10.2 例 2 .................................................................................................................... 65
10.3 例 3 .................................................................................................................... 66
10.4 例 4 .................................................................................................................... 67
11 傅氏级数专项 ................................................................................................................ 69
11.1 典型周期信号 ...................................................................................................... 69
11.1.1 周期方波 1 ................................................................................................ 69
11.1.2 周期方波 2 ................................................................................................ 69
11.1.3 周期脉冲串 ............................................................................................... 70
11.2 例题 .................................................................................................................... 70
12 附录 .............................................................................................................................. 72
12.1 LTI 系统的运算性质 ............................................................................................. 72
12.1.1 交换律 ...................................................................................................... 72
12.1.2 分配率 ...................................................................................................... 72
12.1.3 结合律 ...................................................................................................... 73
12.1.4 微积分性 .................................................................................................. 73
12.1.5 线性时不变性 ........................................................................................... 74
12.2 常用卷积公式 ..................................................................................................... 74
12.3 常见信号的 FT,LT,ZT,DTFT ................................................................................ 75
12.3.1 一般信号 .................................................................................................. 75
12.3.2 奇异信号 .................................................................................................. 75
12.3.3 指数信号 .................................................................................................. 76
12.4 FT,LT,ZT,DTFT 变换性质 ..................................................................................... 77
12.4.1 时移性质 .................................................................................................. 77
12.4.2 频移性质 .................................................................................................. 77
12.4.3 时域尺度变换性质 .................................................................................... 78
12.4.4 时域微积分 ............................................................................................... 78
12.4.5 时间反转 .................................................................................................. 79
12.4.6 频复域微分性质 ........................................................................................ 79
12.5 类 Sinc 函数的频谱 ............................................................................................. 80
IV
12.6 域正反变换总结 .................................................................................................. 81
12.6.1 傅里叶级数（FS） ................................................................................... 81
12.6.2 离散傅里叶变换（DFT） .......................................................................... 82
12.6.3 傅里叶变换（FT） ................................................................................... 82
12.6.4 Laplace 变换 ............................................................................................. 82
12.6.5 Z 变换 ....................................................................................................... 83
12.7 英文简称及符号表示 ........................................................................................... 83
12.7.1 英语简称 .................................................................................................. 83
12.7.2 符号表示 .................................................................................................. 83
V
《信号与系统》考研复习总结
1 序言
1.1 简介
笔者不是专门从事考研资料制作与销售的人员，曾在 2013 年报考了成电（电子科技大学）
电工学院（电子工程学院）信号与信息处理（081002）专业（硕士），专业课当时（同 2018
年）考的是《信号与系统》、《数字电路》；而后在 2016 年报考了成电同一专业的博士，专业
课当时（同 2018）考的是《信号与系统》、《随机过程》。
本文档涵盖了成电 2016 年博士入学考试《信号与系统》大纲，其中部分例题来源于成电
真题。该资料不仅适合报考成电的准硕士和博士，也同样适合报考其他院校的复习者。
该文档旨在节约复习者的复习时间（无需若干轮复习，只需要在本文档的基础上拓展加训
练，不断深入即可），提升复习者的复习效率，最终目标是帮助复习者提升被录取的概率。
该文档是笔者几年的沉淀以及若干个日日夜夜加班加点写成的电子档，其中的每字每句，
每个公式，每张图都是笔者亲自写画，从始至终都没有使用复制粘贴这个功能，目的就是为
复习者提供高质量的复习资料。
文档无论是内容还是排版，都不马虎随意，倾注了笔者不少血汗，所以其价值不会低，若
能花费若干资金，就能较大程度地提升考上的可能性，那是很值得的。
当然，难免出现纰漏，欢迎广大师生和专家给笔者指出，谢谢！
1.2 版权
严格来讲，这个世界上任何作品都没有版权，所谓的版权也只在一个有限的空间和时间
内，表面上属于某个人或某个团体。所以本文档也没有永久的版权。
作者在上传该作品后，会给下载者设置一定的障碍，如果您觉得本文档对您的帮助很大，
想进一步给予作者酬劳，或有其他任何疑问和需要，请致信作者。
联系方式：doudouamtf@qq.com
作者：怪味豆
2018 年 8 月于四川成都
1
2 公共基础知识
这一部分内容可直接背诵，因为当时作者在同时复习《信号与系统》和《随机过程》这 2
门课，发现这部分内容在 2 门课中均会常常涉及到，直接背诵能省很多事，所以命名为：“公
共基础知识”。
2.1 不定积分
, n
∀ ≥ ∈
0
( )
f x
=
( )
x
=
′
f
n
( )
h x
( )
g x
( )
( )
′
h x g x
−
( )
g x
′
( )
( )
nh x g x
1
+
n
{
e
e
( )
g x
ax
( )
f x
( )
g x
=
e
ax
e
⋅
′
f
f
⋅
( )
x
′
( )
x
+
( )
′
g x f x
( )
+
( )
af x
,
∀ ∈
a
}
′
( )
f x
′
=
(
(
sin
cos
∫
∫
∫
∫
(
(
x
x
cos
sin
2
2
)
x dx
)
x dx
=
=
1
2
1
2
x
+
x
−
1
4
1
4
sin 2
x
sin 2
x
x
+
=
=
cos
sin
x
sin
x
cos
x
x
−
x
)
x dx
)
x dx
1
a
1
a
x
x
ax
e
x
)
dx
=
e
ax
ax
x
2
e
)
dx
=
e
ax
(
(
∫
∫
−
1
2
a
2
−
,
2
2
a
∀ ≠ ∈
a
0
x
+
2
3
a
,
∀ ≠ ∈
a
0
e sin
ax
(
bx dx
)
=
e cos
ax
(
bx dx
)
=
∫
∫
b
+
b
+
2
a
2
a
ax
e
2
b
ax
e
2
b
a
b
a
b
sin
(
bx
)
−
cos
(
bx
cos
(
bx
)
+
sin
(
bx
b
≠ ∈
0
,
a
∈
)
b
≠ ∈
0
,
a
∈
)
) (
) (
∫
1
x
dx
=
2
x
(1)
(2)
(3)
(4)
(5)
(6)
(7)
2
1
1
2.2 定积分
π θ θ=
(
sin
d
)
∫
0
2
(8)
sinθ
2
2
2
2
1
−
2
2
0
π
4
1
−
2
2
3
π
4
π
2
π
θ
)
θ θ=
d
(
2
sin
π
2
π
∫
0
2
sin θ
π
8
+
1
4
π
8
+
1
4
π
8
−
1
4
π
4
0
−
1
4
π
8
3
π
4
π
θ
π
2
1
a
=
1
2
a
+∞ −
e
0
ax
dx
=
+∞
−
ax
e
x
dx
∫
∫
0
(
a
>
0
)
t
−
α
dt
+∞
⋅
t
β
e
∫
0
(
α β
0,
>
∈
!
β
=
1
+
β
α
)
+
(9)
(10)
(11)
3
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
