第1页 / 共29页
第2页 / 共29页
第3页 / 共29页
第4页 / 共29页
第5页 / 共29页
第6页 / 共29页
第7页 / 共29页
第8页 / 共29页
数学建模+送货策略+论文+源码.doc
1
快递公司送货策略
一 摘要：
本文是关于快递公司送货策略的优化设计问题，即在给定送货地点和给定设计规范的条件下，确定
所需业务员人数，每个业务员的运行线路，总的运行公里数，以及费用最省的策略。 本文主要从
最短路经和费用最省两个角度解决该问题，建立了两个数据模型。模型一：利用“图”的知识，将
送货点抽象为“图”中是顶点，由于街道和坐标轴平行，即任意两顶点之间都有路。在此模型中，
将两点之间的路线权值赋为这两点横纵坐标之和。如 A（x1，y1），B（x2，y2）两点，则权值为
D=|x2-x1|+|y2-y1|。并利用计算机程序对以上结果进行了校核。模型二：根据题意，建立动态规
划的数学模型。然后用动态规划的知识求得最优化结果。根据所建立的两个数学模型，对满足设计
要求的送货策略和费用最省策略进行了模拟，在有标尺的坐标系中得到了能够反映运送最佳路线的
模拟图。最后，对设计规范的合理性进行了充分和必要的论证。
二 关键词：
快递公司送货 最优化 图模型 多目标动态规划 TSP 模型
三 问题重述：
在快递公司送货策略中，确定业务员人数和各自的行走路线是本题的关键。这个问题可以描述为:一中
心仓库(或配送调度中心) 拥有最大负重为 25kg 的业务员 m 人, 负责对 30 个客户进行货物分送工作,
客户 i 的快件量为已知 , 求满足需求的路程最短的人员行驶路径,且使用尽量少的人数,并满足以下
条件:
1) 每条送快件的路径上各个客户的需求量之和不超过个人最大负重。
2) 每个客户的需求必须满足, 且只能由一个人送货.
3）每个业务员每天平均工作时间不超过 6 小时，在每个送货点停留的时间为 10 分钟，途中速度为
25km/h。
4）为了计算方便，我们将快件一律用重量来衡量，平均每天收到总重量为 184.5 千克。
表一为题中所给的数据：
表一
最大载重量
途中的平均速度
业务员工作时间上限 6h
每个送货点停留时间 10min
备注
1、快件一律用重量来衡量 2、假定街道方向均平行于坐标轴
25kg
25km/h
重载时速
重载酬金
空载时速
空载酬金
20km/h
3 元/km*kg
30km/h
2 元/km
2
处于实际情况的考虑, 本研究中对人的最大行程不加限制.本论文试图从最优化的角度，建立起满足设
计要求的送货的数学模型，借助于计算机的高速运算与逻辑判断能力，求出满足题意要求的结果。
四 问题分析：
从公司总部配出一个人，到任意未配送的送货点，然后将这个人配到最近的未服务的送货点范围之内的
邻居，并使送货时间小于 6 小时，各送货点总重量不超过 25kg。继续上述指派，直到各点总重量超过
25kg，或者送货时间大于 6 小时。最后业务员返回总部，记录得到的可行行程（即路线）。对另一个业
务员重复上述安排，直到没有未服务的送货点。对得到的可行的行程安排解中的每一条路径，求解一个
旅行商问题，决定访问指派给每一条行程的业务员的顺序，最小化运输总距离。得到可行解的行程安排
解后退出。
根据题意的要求，每个人的工作时间不超过 6 小时，且必须从早上 9 点钟开始派送，到当天 17 点之前
（即在 8 小时之内）派送完毕。且
5.
184
kg
25
kg
8
点间的距离。
，故至少需要 8 条路线。表二列出了题中任意两配送
表二：任意两点间的距离矩阵
3
因为距离是对称的，即从送货点 i 到送货点 j 的距离等于从 j 到 i 的距离。记作：dij.
表三给出了客户的需求，为了完成送快递的任务，每个人在工作时间范围内，可以承担两条甚至
更多的线路。表中给出了送货点序号，送货点编号，快件量 T，以及送货点的直角坐标。
序号 送货点 快件量 T 坐标（km） 序号 送货点 快件量 T 坐标（km）
表三
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
6
5
7
8
9
10
11
12
13
14
20
x
3
1
5
4
0
3
7
9
10
14
17
14
12
10
7
y
2
5
4
7
8
11
9
6
2
0
3
6
9
12
14
8
8.2
6
5.5
3
4.5
7.2
2.3
1.4
6.5
4.1
12.7
5.8
3.8
4.6
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
16
17
18
19
15
32
22
23
24
25
26
27
28
29
30
x
2
6
11
15
19
22
21
27
15
15
20
21
224
25
28
Y
16
18
17
12
9
5
0
9
19
14
17
13
20
16
18
3.5
5.8
7.5
7.8
3.4
6.2
6.8
2.4
7.6
9.6
10
12
6.0
8.1
4.2
五 模型假设：
（1）街道方向均平行于坐标轴，且在该前提下，业务员可以任意选择路线。
（2）无塞车现象，即业务员送快递途中不受任何外界因素影响，且业务员的休息时间不包括在最大工
作时间 6 个小时内。
（3）业务员人数不限制。
（4）每个业务员的路线一旦确定，便不再更改。
（5）每个业务员送快递是独立的，每人之间互不影响。
（6）业务员到某送货点后必须把该送货点的快件送完。
（7）每个业务员每天的工作时间不超过 6 个小时。
（8）业务员回到快递公司后停留一个小时。
4
六 主要符号说明：
Ti：序号为 i 的送货点的快件重量
（xi ，yi）序号为 i 的送货点的坐标
M 重：业务员送货总重载费用
M 空：业务员送货总空载费用
M 总：业务员送货总费用
N：业务员送货的总次数
m：业务员人数
mj：第 j 个业务员送货的次数
i
,1
0
，业务员在序号为
业务员在序号为
ai
的送货点送快件
i
的送货点没有送快件
bi
k
第 条路线选择序号为 的送货点是最远点
1,
0
，第 条路线选择序号为 的送货点不是最远点
k
i
i
七 模型建立与求解：
7.1 问题一模型
本模型考虑用多目标动态规划求解。由于问题一中只要求给出一个合理的方案，且未涉及到业务员工资
问题，故只要满足条件——业务员的工作时间上限是 6 个小时以及每条路线的最大载重量不大于 25kg
即可，本模型中追加两个目标——路程最短和人员最少。可以通过以下两种方法实现：（1）每一个行
程的第一个送货点是距离总部最近的未服务的送货点。用这种方法，即可得到一组运行路线，总的运行
公里数，以及总费用。（2）每一个行程的第一个送货点是距离总部最远的未服务的送货点。然后以该
点为基准，选择距它最近的点，加上约束条件，也可得到一组数据。然后比较两组结果，通过函数拟合
即可得到最优化结果。
本模型中以满足需求的路程最短的人员行驶路径,且使用尽量少的人数，即
(2*bi*(xi+yi))
且 min m
min
N 30
k 1 i 1
约束条件为：
1 时间约束：
mj
1j
(2(
xi
25
yi
)
1
6
30
i
1
ai
)
6
2 载重量约束：
Ti
*
ai
25
方法一：每一个行程的第一个送货点是距离总部最近的未服务的送货点。
5
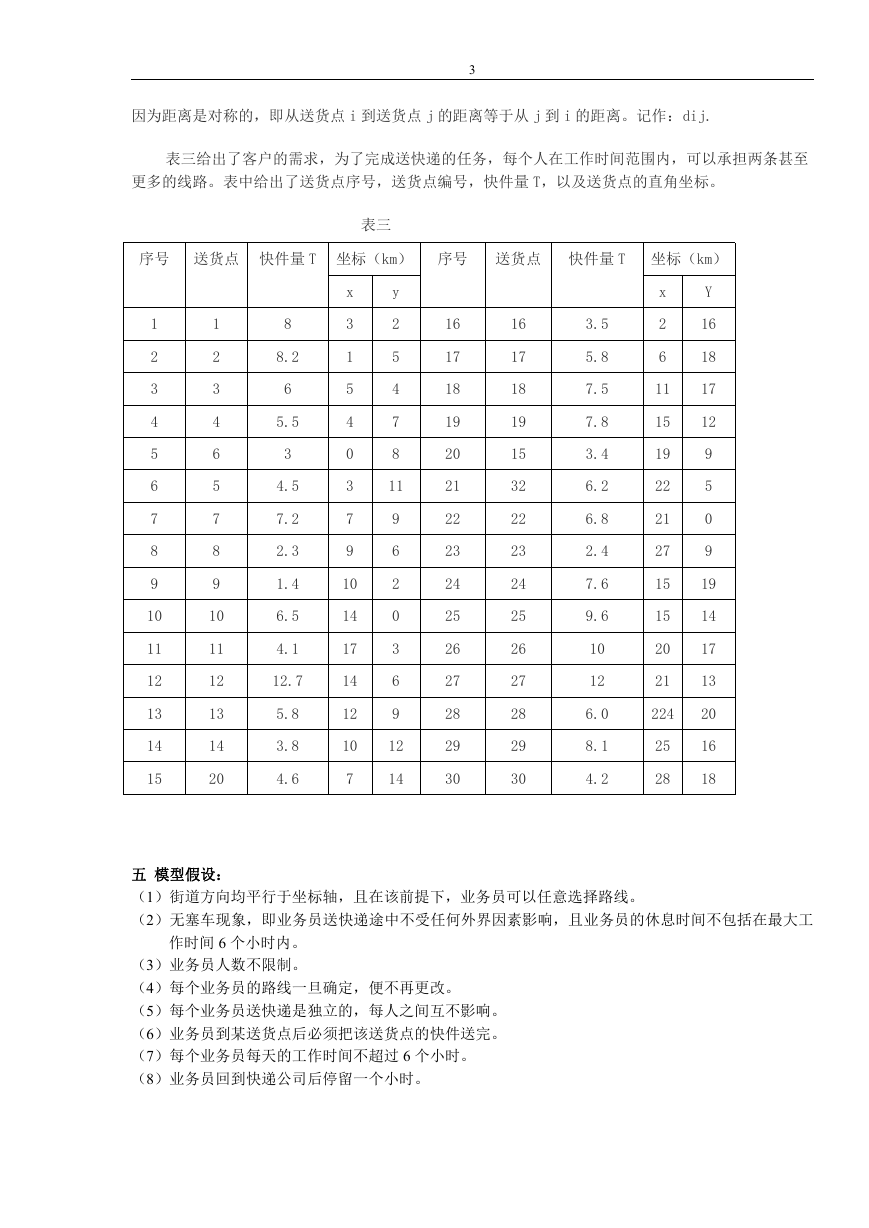
开始
找离原该点最近的点 v，且
该点的访问标志设为被访
问，该点快递重量为 w，输
出该点。
找点 v 最近的点，快递重量
为 w1，且 w1+w<25，当其不
成立时找次远点。
Y
找到符合条件的点，且不
止一个时选择快递重量最
重的那个点，访问标志设
为被反问，并输出该点，
赋值给 v，且 w=w+w1；
N
找 不
到 符
合 条
件 的
点 时
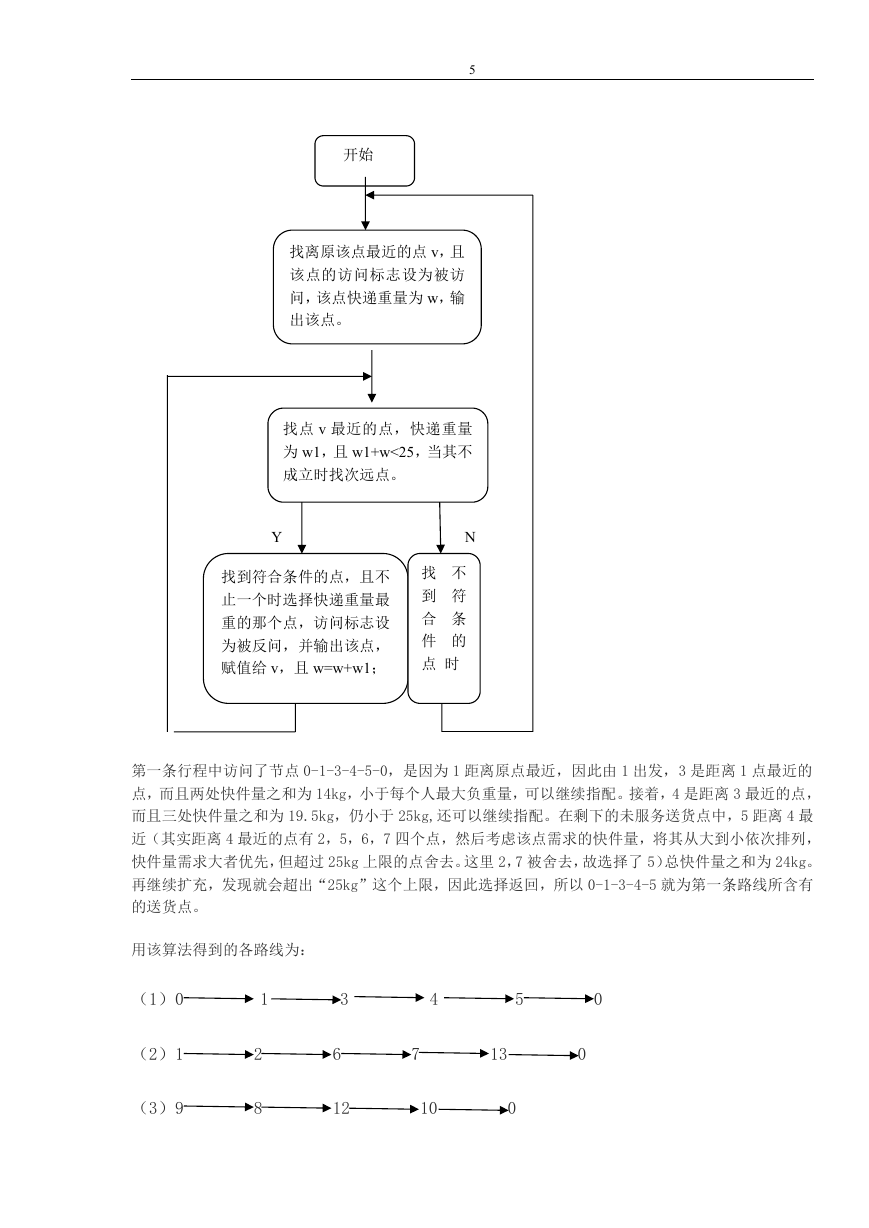
第一条行程中访问了节点 0-1-3-4-5-0，是因为 1 距离原点最近，因此由 1 出发，3 是距离 1 点最近的
点，而且两处快件量之和为 14kg，小于每个人最大负重量，可以继续指配。接着，4 是距离 3 最近的点，
而且三处快件量之和为 19.5kg，仍小于 25kg,还可以继续指配。在剩下的未服务送货点中，5 距离 4 最
近（其实距离 4 最近的点有 2，5，6，7 四个点，然后考虑该点需求的快件量，将其从大到小依次排列，
快件量需求大者优先，但超过 25kg 上限的点舍去。这里 2，7 被舍去，故选择了 5）总快件量之和为 24kg。
再继续扩充，发现就会超出“25kg”这个上限，因此选择返回，所以 0-1-3-4-5 就为第一条路线所含有
的送货点。
用该算法得到的各路线为：
（1）0
（2）1
（3）9
1
2
8
3
6
12
4
5
0
7
13
0
10
0
（4）0
16
17
20
14
15
23
0
6
（5）0
（6）0
（7）0
（8）0
11
27
18
29
22
26
24
28
32
0
25
30
19
0
0
0
现在 0-1-3-4-5 这四个送货点之间的最优访问路径安排就是一个典型的单回路问题。可以通过单回路
运输模型-TSP 模型求解。一般而言，比较简单的启发式算法求解 TSP 模型求解有最邻近法和最近插入
法两种。由 RosenkrantzStearns 等人在 1977 年提出的最近插入法，能够比最近邻点法，取得更满意的
解。由于 0-1-3-0 已经先构成了一个子回路，现在要将节点 4 插入，但是客户 4 有三个位置可以插入，
现在分析将客户 4 插入到哪里比较合适:
1.插入到（0，1）间，C 总= 7+4+5+1+4+9=30。
2.插入到（1，3）间，C 总=5+6+4+9=24。
3.插入到（3，0）间，C 总=5+4+4+11=24。
比较上述三种情况的增量，插入到（3，0）间和（1，3）间增量最小，考虑到下一节点插入时路程最小
问题，所以应当将 4 插入到送货点 3 和总部 0 之间。接下来，用同样的方法，将 5 插到 4 和 0 之间，能
使该条路线总路程最小，该路线总路程为 32km，历时 1.9467h。结果子回路为 T={0-1-3-4-5-0}.因为
街道平行于坐标轴方向，所以它就是最优化路线。
第二条行程这中，由于所剩下节点中，2 距离 0 点最近，因此由 2 出发，就可以找到最近点 13，接着是
7，然后 6.这样，第二条优化路线 0-2-13-7-6-0 就确定了。用这种方法，依次可确定以下剩余六条路
线。
得到总的送货路线为：
（1）0
（2）0
（3）0
（4）0
（5）0
（6）0
（7）0
1
3
4
5
0
2
10
16
19
18
27
13
12
17
11
24
26
7
8
20
32
25
0
0
0
15
0
6
9
14
22
0
23
0
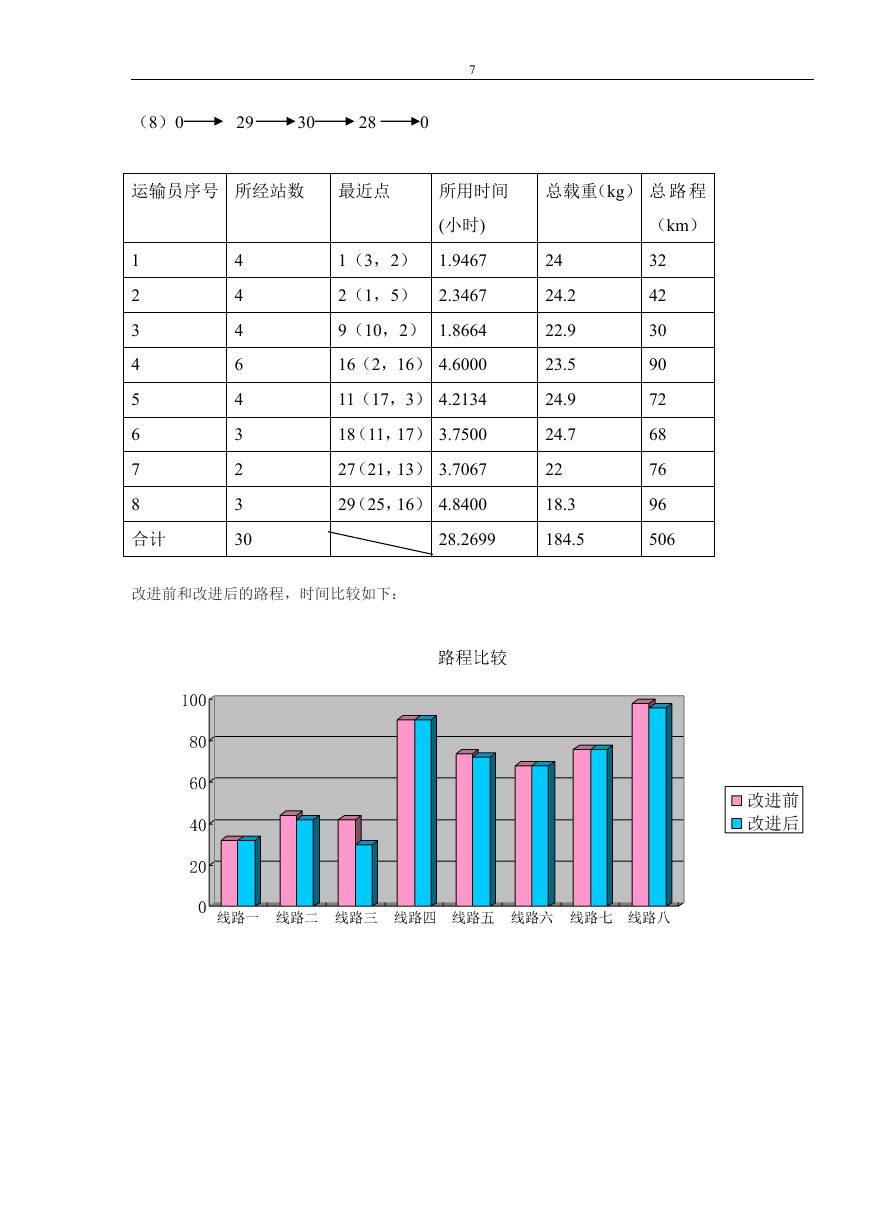
（8）0
29
30
28
0
7
运输员序号 所经站数 最近点
所用时间
1
2
3
4
5
6
7
8
合计
4
4
4
6
4
3
2
3
30
(小时)
1（3，2） 1.9467
2（1，5） 2.3467
9（10，2） 1.8664
16（2，16） 4.6000
11（17，3） 4.2134
18（11，17） 3.7500
27（21，13） 3.7067
29（25，16） 4.8400
28.2699
改进前和改进后的路程，时间比较如下：
总载重（kg） 总 路 程
（km）
32
42
30
90
72
68
76
96
506
24
24.2
22.9
23.5
24.9
24.7
22
18.3
184.5
8
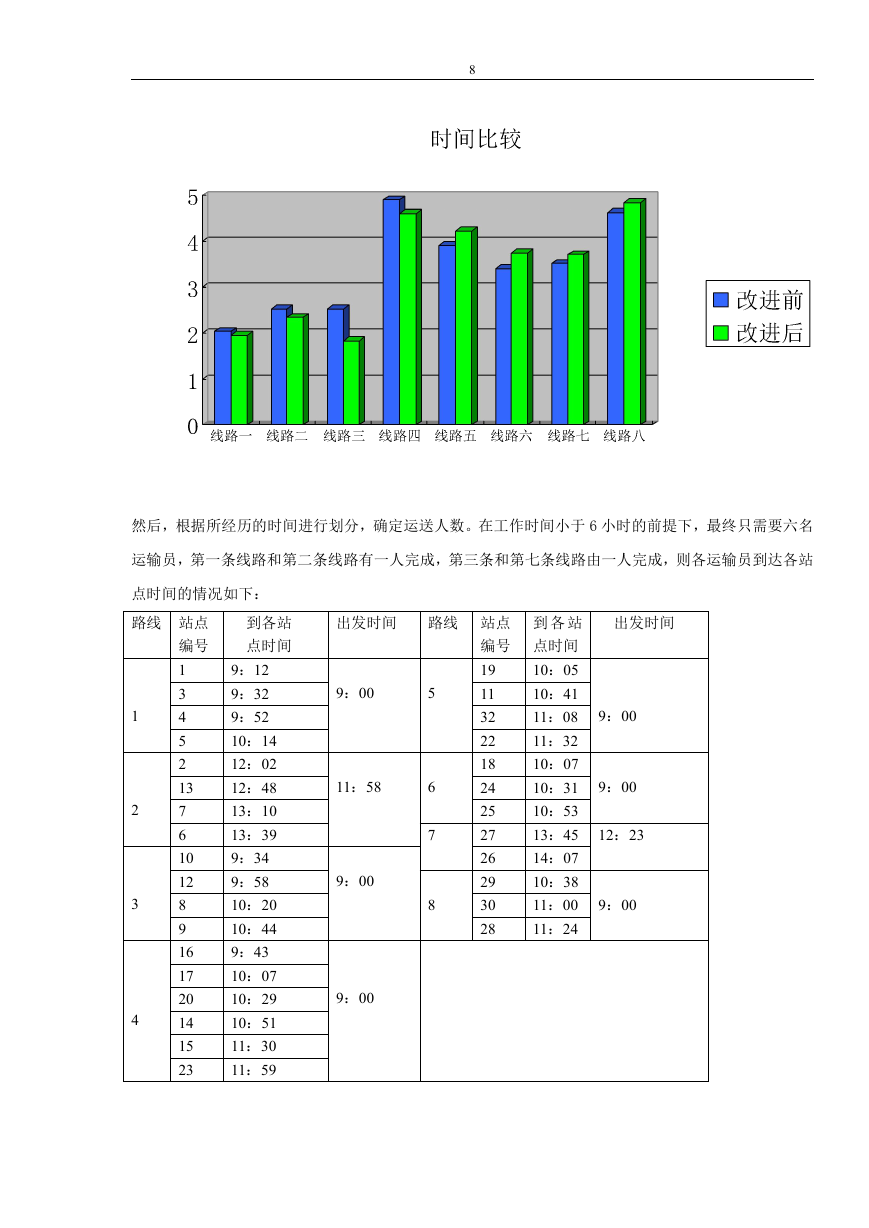
然后，根据所经历的时间进行划分，确定运送人数。在工作时间小于 6 小时的前提下，最终只需要六名
运输员，第一条线路和第二条线路有一人完成，第三条和第七条线路由一人完成，则各运输员到达各站
点时间的情况如下：
2
1
路线 站点
编号
1
3
4
5
2
13
7
6
10
12
8
9
16
17
20
14
15
23
3
4
5
路线 站点
编号
19
11
32
22
18
24
25
27
26
29
30
28
6
7
8
出发时间
9：00
9：00
12：23
9：00
到 各 站
点时间
10：05
10：41
11：08
11：32
10：07
10：31
10：53
13：45
14：07
10：38
11：00
11：24
到各站
点时间
出发时间
9：00
11：58
9：00
9：00
9：12
9：32
9：52
10：14
12：02
12：48
13：10
13：39
9：34
9：58
10：20
10：44
9：43
10：07
10：29
10：51
11：30
11：59
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
