第1页 / 共34页
第2页 / 共34页
第3页 / 共34页
第4页 / 共34页
第5页 / 共34页
第6页 / 共34页
第7页 / 共34页
第8页 / 共34页
2009年注册电气工程师供配电专业基础考试真题及答案.doc
2009 年注册电气工程师供配电专业基础考试真题及答案
一、单项选择题（共 60 题，每题 2 分。每题的备选项中只有一个最符合题意。）
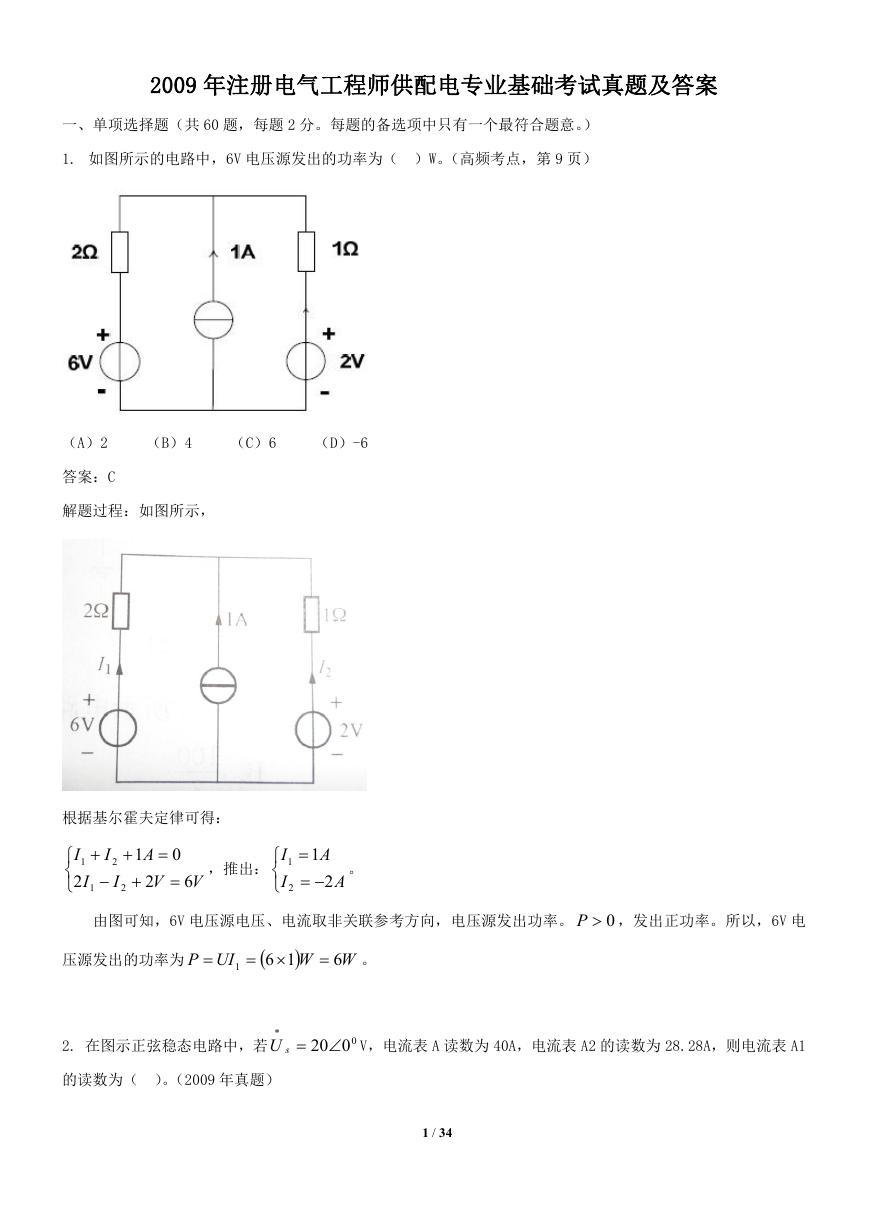
1. 如图所示的电路中，6V 电压源发出的功率为（ ）W。（高频考点，第 9 页）
（A）2
（B）4
（C）6
（D）-6
答案：C
解题过程：如图所示，
根据基尔霍夫定律可得：
I
1
2
I
I
1
1
2
A
2
V
0
2
I
6
V
，推出：
I
I
1
2
1
A
2
A
。
由图可知，6V 电压源电压、电流取非关联参考方向，电压源发出功率。
0P ，发出正功率。所以，6V 电
压源发出的功率为
P
UI
1
16
WW
6
。
2. 在图示正弦稳态电路中，若
*
20sU
0
0
的读数为（ ）。（2009 年真题）
V，电流表 A 读数为 40A，电流表 A2 的读数为 28.28A，则电流表 A1
1 / 34
（A）11.72A （B）28.28A
（C）48.98A （D）15.28A
答案：B
解题过程：由题意可知，
I
1
2
I
I
2
2
2
40
28.28
2
28.28
A
。
3. 图示电路原已稳定， 0t
时闭合开关 S 后，则 t
iL 为：（ ）。（高频考点，第 66 页）
（A）
9.05.1
e
4000
t
A
（B）
5.19.0
Ae t
（C）0（D）
9.05.1
e
4000
t
A
答案：D
解题过程：（1）开关 S 未合上前，电路如下图(a)所示。
2 / 34
则电流为：
0
iL
6
10
根据换路定则，可知：
0
i
L
10
10
i
L
5
0
A
6
4.2
10
25
A
A
4.2
A
。
。
（2）开关 S 闭合后，电路进入稳态，如下图所示。
可得电流为：
iL
6
10
10//10
5
10
（3）求时间常数，据图(c)求得：
10
10
10
A
5.1
A
R
10
//
10
可求得：
25.0
310
10
L
R
10
5
004
.0
H
16
15
15
16
10
6
10
10
s
（4）根据三要素公式可求得：
t
i
L
i
L
i
L
0
i
L
t
e
5.1
5.14.2
e
t
25.0
10
3
9.05.1
e
4000
t
A
。
4. 在图示正弦稳态电路中，若电压表读数为 50V，电流表读数为 1A，功率表读数为 30W，则 R、 L 为：（ ）。
（高频考点，第 51 页）
（A） 20 ， 45
（B） 25 ， 25
（C） 30 ， 40
（D） 10 ， 35
答案：C
解题过程：功率表的读数是有功功率，即电阻 R 上消耗的功率，由
RIP
2
，得
R
30
。
3 / 34
据
UZ
I
50
50
1
2
R
L
2
，求得：
L
40
。
5. 图示电路为含耦合电感的正弦稳态电路，开关 S 断开时，
U 为（ ）。（高频考点，第 52 页）
（A）
10
2
V045
（B）
10
2
V045
（C）
答案：A
解题过程：当开关 S 断开时，则有：
10
2
V030
（D）
10
2
V030
jU
10
20
10
0
0
10
j
10
j
0
0
20
2
45
10
10
90
0
2
0
45
10
2
45
0
V
。
0
6. 图示电路为三相对称电路，相电压为 200V，
Z
1
Z
L
150
150
j
，IA 为：（ ）。（高频考点，第 54 页）
（A）
2
A045
（B）
2
A045
（C）
2
2
A045
（D）
2
2
A045
答案：A
解题过程：设
U A
200
00
V
，负载 1Z 进行 Y
转换后，其 A 相电路如下图所示。
4 / 34
根据 A 相电路图可得：
I
A
U
A
Z
L
Z
1
3
150
200
150
j
0
0
150
150
j
3
200
j
200
200
2
2
45
0
A
。
7. 图示电路中，若
tus
tu
15
2
cos
1000
t
10
V
045
15
2
cos
1000
t
0
45
20
2
2000
t
0
20
V
，
，
R
10
，
L
1
1
mH
，
L
2
mH
，则 1C 为：（ ）。（高频考点，第 49 页）
cos
2
3
（A） F75
（B）
F200
（C）
F250
（D）
F150
答案：C
解题过程：二次谐波作用时，电路发生并联谐振，电路开路，R 的电压 u 无二次谐波分量。
则：
2
L
1
1
2
C
1
，
C
1
1
2
4
L
1
1
1000
.0
001
1
4000
4
1000
5.2
10
4
F
250
F
8. 图示电路中，若
u
5.0
V
，
i 1 ，则 R 为：（ ）。（高频考点，第 20 页）
A
5 / 34
（A）
1
3
答案：B
（B）
1
3
（C）
1
2
（D）
1
2
解题过程：上图电路可以简化为下图：
据图(a)可得：
Req
u
i
5.0
1
5.0
（1）
求等效电阻，将图(a)中的 2V 电压源短路，电路如图(b)所示。
根据图(b)可得：
根据图(b)可得：
Req
RR
//
R
5.1
R
（2），
6 / 34
根据式（1）、（2）可求得：
5.1 R
5.0
，
1R
3
。
9. 图示电路中的电压 u 为：（ ）。（高频考点，第 6 页）
（A）49V
（B）-49V
（C）29V
（D）-29V
答案：A
解题过程：根据电路图，
总电阻
3R
10
10
20
20
49
V
20
20
10
10
3
200
30
200
30
3
400
30
90
400
30
490
30
49
3
。
u
IR
3
49
3
10. 图示正弦稳态电路角频率为
1000
rad /
s
，N 为线性阻抗网络，其功率因数为 0.707（感性），吸收的有功功
率为 500W，若要使 N 吸收的有功功率达到最大，则需在其两端并联的电容 C 应为：（ ）。（高频考点，第 39 页）
（A） F50
（B） F75
（C）
F100
（D）
F125
答案：C
解题过程：根据题图可得 N 为线性阻抗网络，其功率因数为 0.707（感性），
因此，其总功率
S
500
.0
707
W
707
W
，其无功功率
Q
2
707
500
2
249849
500
W
。
于是得：
R
jX
R
jR
。
7 / 34
电流
I
U
10
j
10
Z
200
10
j
0
0
R
jR
10
，有效值
I
200
102
2
R
，
线性网络吸收的有功功率
RIP
2
40000
102
R
2
R
500
W
，得
R
10
。
R
jX
//
j
1
1000
C
10
10
j
//
j
1
1000
C
10
10
j
10
10
j
j
C
j
1
1000
1
1000
C
要使 N 吸收的有功功率最大，电路呈纯阻性，则须满足
Z
Z eq
（Z 的共轭）：
10
10
j
10
10
j
j
j
1
1000
C
1
1000
C
10
10
j
10
10
j
10
10
j
j
10
整理上式得：
100
10
j
10
100
100
j
j
200
再次整理上式得：
j
1
100
C
1
100
C
10
j
1
1000
C
1
1000
C
1
100
C
1
j
100
C
1
100
C
1
1000
C
100
j
10
10
1
1000
C
100
j
100
1
100
C
200
1
100
C
j
1
100
C
200
C
1
C50
1
200
1
10000
.0
0001
F
100
F
。
50
11. 在图示正弦交流电路中，若电源电压有效值
U 100
V
，角频率为，电流有效值
I
I
1
I
2
，电源提供
的有功功率
P 866
W
，则电阻 R 为：（ ）。（高频考点，第 38 页）
8 / 34
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
