最全的有限元介绍.pdf

发布时间：2022-06-06 发布人：admin 分类：说明书资料大小：4.95M 资料格式：pdf 举报版权申诉

weiyiwen1982-10378436-16359647393591524798.pdf-第1页.png

第1页 / 共28页

weiyiwen1982-10378436-16359647393591524798.pdf-第2页.png

第2页 / 共28页

weiyiwen1982-10378436-16359647393591524798.pdf-第3页.png

第3页 / 共28页

weiyiwen1982-10378436-16359647393591524798.pdf-第4页.png

第4页 / 共28页

weiyiwen1982-10378436-16359647393591524798.pdf-第5页.png

第5页 / 共28页

weiyiwen1982-10378436-16359647393591524798.pdf-第6页.png

第6页 / 共28页

weiyiwen1982-10378436-16359647393591524798.pdf-第7页.png

第7页 / 共28页

weiyiwen1982-10378436-16359647393591524798.pdf-第8页.png

第8页 / 共28页

Generalized Multiscale Finite-Element Method (GMsFEM) for elastic wave propagation in heterogeneous, anisotropic media

1 Introduction

2 Theory

2.1 Weak form of the elastic wave equation

2.1.1 Elastic wave equation

2.1.2 CG formulation

2.1.3 DG formulation

2.2 Multiscale basis functions

2.2.1 Type I

2.2.2 Type II

2.2.3 Oversampling

2.3 Stability condition and dispersion relation

2.4 Implementation

2.4.1 Semi-discrete form of the GMsFEM

2.4.2 Absorbing boundary conditions

2.4.3 Adaptability in choosing the number of basis functions

2.4.4 A global projection approach

2.4.5 Time stepping

2.4.6 Source term

3 Numerical results

3.1 VTI-TTI-isotropic three-layer heterogeneous model

3.2 Randomly heterogeneous anisotropic medium model with curved boundaries

3.3 Heterogeneous model: adaptive assignment of number of basis functions

4 Discussions

5 Conclusions

Acknowledgements

Appendix A The solution to local problem 22

References

Journal of Computational Physics 295 (2015) 161–188 Contents lists available at ScienceDirect Journal of Computational Physics www.elsevier.com/locate/jcp Generalized Multiscale Finite-Element Method (GMsFEM) for elastic wave propagation in heterogeneous, anisotropic media Kai Gao a,∗,1, Shubin Fu b, Richard L. Gibson Jr. a, Eric T. Chung d, Yalchin Efendiev b,c a Department of Geology and Geophysics, Texas A&M University, College Station, TX 77843, USA b Department of Mathematics, Texas A&M University, College Station, TX 77843, USA c Numerical Porous Media SRI Center (NumPor), King Abdullah University of Science and Technology, Thuwal, Saudi Arabia d Department of Mathematics, The Chinese University of Hong Kong, Shatin, NT, Hong Kong a r t i c l e i n f o a b s t r a c t Article history: Received 31 August 2014 Received in revised form 29 March 2015 Accepted 31 March 2015 Available online 14 April 2015 Keywords: Elastic wave propagation Generalized Multiscale Finite-Element Method (GMsFEM) Heterogeneous media Anisotropic media It is important to develop fast yet accurate numerical methods for seismic wave propagation to characterize complex geological structures and oil and gas reservoirs. However, the computational cost of conventional numerical modeling methods, such as ﬁnite-difference method and ﬁnite-element method, becomes prohibitively expensive when applied to very large models. We propose a Generalized Multiscale Finite-Element Method (GMsFEM) for elastic wave propagation in heterogeneous, anisotropic media, where we construct basis functions from multiple local problems for both the boundaries and interior of a coarse node support or coarse element. The application of multiscale basis functions can capture the ﬁne scale medium property variations, and allows us to greatly reduce the degrees of freedom that are required to implement the modeling compared with conventional ﬁnite-element method for wave equation, while restricting the error to low values. We formulate the continuous Galerkin and discontinuous Galerkin formulation of the multiscale method, both of which have pros and cons. Applications of the multiscale method to three heterogeneous models show that our multiscale method can effectively model the elastic wave propagation in anisotropic media with a signiﬁcant reduction in the degrees of freedom in the modeling system. Published by Elsevier Inc. 1. Introduction Seismic wave propagation has long been a fundamental research ﬁeld in both global scale seismology and reservoir ex- ploration scale seismics. There are two basic categories of methods to investigate the propagation of waves through the Earth media, approximate methods and the full waveﬁeld (exact) methods. Approximate methods rely on either the simpliﬁcation of the Earth media, or the approximation of the wave equation, which include, for instance, the ray tracing method [14,9,47], the Gaussian beam method [55,50], the one-way wave equation approach [22,104], the reﬂectivity method [62], etc. These methods are generally fast and computationally affordable. However, they are intrinsically incomplete and therefore may fail * Corresponding author. E-mail addresses: kaigao87@gmail.com (K. Gao), shubinfu89@gmail.com (S. Fu), gibson@tamu.edu (R.L. Gibson), tschung@math.cuhk.edu.hk (E.T. Chung), efendiev@math.tamu.edu (Y. Efendiev). 1 Current address: Geophysics Group, Los Alamos National Laboratory, Los Alamos, NM 87545, USA. http://dx.doi.org/10.1016/j.jcp.2015.03.068 0021-9991/Published by Elsevier Inc.

162 K. Gao et al. / Journal of Computational Physics 295 (2015) 161–188 in complex geology, where steep dips, faults, salt bodies, irregular interfaces, or fractures exist. The direct methods on the other hand, consist of many different numerical methods to solve various forms of the wave equation directly without ap- proximations and simpliﬁcations, including, for example, the ﬁnite-difference method [27,99,89], the ﬁnite-element method [76,32,66,15], the pseudo-spectral method [44], and so on, and are essential fundamentals of full-waveﬁeld based seismic imaging and inversion methods, such as reverse-time migration [78,94] and full waveform inversion [95,100,93]. However, the applications of full waveﬁeld methods are also computationally expensive, where the computation costs are directly proportional to the number of discrete elements that are required to represent the geological model, and this makes the wide applications of full-waveﬁeld based imaging and inversion methods infeasible for realistic large 2D and 3D geological models. Moreover, the Earth medium should be considered as a complex system that is heterogeneous at different spatial scales. To include the inﬂuence of heterogeneities at ﬁner scales when simulating the wave propagation on coarser scale, researchers tend to apply various effective medium theories [6,92,91] to get a set of equivalent parameters that is supposed to best approximate the properties of the heterogeneous media. However, all of these effective medium theories rely on a long wavelength assumption, i.e., size of the heterogeneities is much smaller than the dominant wavelength of the wavelet, and when such assumptions fail, wave reﬂections and scattering become important, which cannot be correctly modeled by the effective medium approach. In this paper, we are interested in developing fast yet accurate full waveﬁeld modeling method for elastic wave propa- gation in heterogeneous, anisotropic media. The most straightforward way to model various types of wave equations is the ﬁnite-difference method due to its simplicity in implementation, where we have the conventional central ﬁnite-difference method (FDM) [3,2,61,27,73], the staggered-grid ﬁnite-difference method [99,71], the rotated staggered-grid method [89,88], etc. However, FDM enjoys less ﬂexibility in handling unstructured meshes, hanging nodes, and non-conforming meshes, and free surface topography problem, and only recently, the mimetic ﬁnite-difference method [72,31] claims be able to achieve this goal, yet there are corresponding increases in computational costs and decreases in required time step size due to the distortion of grids. The ﬁnite-element methods (FEM), on the other hand, provide an effective solution to deal with the unstructured mesh of the geological model, which can honor the curved interfaces of the geological bodies, or the complex fault systems. The FEM also introduces great beneﬁts for dealing with free surface topography that can be naturally satisﬁed through the weak formulation of the FEM. Various FEM techniques have been developed. Some of the earliest efforts to solve the wave equation with the FEM are conventional continuous Galerkin (CG) FEMs [10,76,57,32]. However, CG-FEM can be quite computationally expensive due to the requirement of inverting the global mass matrix, which is not diagonal or block diagonal without mass lumping. This problem is removed with the spectral-element method (SEM) [83,67,68,65,66, 63,24,25], which adopts Gauss–Lobatto–Legendre (GLL) integration points to obtain a strictly diagonal global mass matrix. Nevertheless, CG-FEM requires the continuity of waveﬁeld solutions at the edges of elements, and is therefore less accurate when describing the wave propagation across high-contrast interfaces or discontinuities in the model. Besides, CG-FEM is unable to handle mesh discretization that is composed of different types of elements, non-conforming mesh or hanging nodes. These problems are naturally solved with the discontinuous Galerkin (DG) FEM initially developed for the transport equation [85] and elliptic partial differential equations [101,87,5]. The DG-FEM has gradually gained broader applications in time-dependent problems such as wave equations [51,15,16,59,33,29,30,34,103]. Importantly, DG-FEM has the advantage over CG-FEM that the global mass matrix is block diagonal, and the support of elements is distinct, a feature that favors straightforward parallel implementation, and this is quite important for wave equation simulations in large models. How- ever, DG-FEM also suffers from some drawbacks, such as more complicated error and dispersion analyses, the requirement of tuning penalty parameters and much more degrees of freedom. Regardless of the implementation complexity, neither FDMs nor FEMs addressed the common issue of high computational cost when solving the wave equation in large models. One approach to reduce such costs is the so-called multiscale method. The multiscale method was originally designed for elliptic partial differential equations [56]. Unlike all the above mentioned FEMs, the multiscale FEM (MsFEM) seeks special basis functions, i.e., the multiscale basis functions, to include the inﬂuence of ﬁne-scale heterogeneity when solving the PDEs on the coarse scale, and the usage of the multiscale basis functions enables the MsFEM to consider high contrasts in medium properties that may vary by several orders of magnitudes spatially. These multiscale basis functions are not predeﬁned polynomials like those in conventional FEMs (e.g., [7]). Instead, they are solved from appropriately deﬁned local problems [56,40,58]. Chung et al. [19,20] and Gibson et al. [48] applied the idea of the multiscale basis functions and designed a multiscale method for mixed-form (pressure-velocity form) acoustic wave equation. To improve the accuracy of the MsFEM, Efendiev et al. [39,37] proposed to utilize multiple multiscale basis functions solved from local spectral problem, which is the generalized multiscale ﬁnite-element method (GMsFEM). These basis functions are constructed from the eigenfunctions that correspond to the ﬁrst several smallest eigenvalues of the local spectral problem, and are therefore correspond to the local eigenmodes with lowest frequencies. Chung et al. [17] proposed a discontinuous Galerkin (DG) GMsFEM for the second-order acoustic wave equation, where they constructed so-called interior basis and boundary basis functions to capture ﬁne-scale media heterogeneity information for the waveﬁeld simulation on coarse scale. This DG-GMsFEM was also strictly analyzed by Chung et al. [21]. There are other methods titled “multiscale”, yet they begin with different assumptions and methodologies, for instance, the operator-based upscaling for the acoustic wave equation [4,98]. Korostyshevskaya and Minkoff [69] and Vdovina and Minkoff [96] analyzed the error and convergence characteristics of this approach. However, in their approach, local problems have to be solved at each time step, whereas in the multiscale approach by Chung et al. [20,21], the local problems only need to be solved once before the time stepping to get the multiscale basis functions. Vdovina et al. [97] developed a similar operator-based upscaling

K. Gao et al. / Journal of Computational Physics 295 (2015) 161–188 163 approach for elastic wave equation. Owhadi and Zhang [80–82] proposed the multiscale method for the wave equation based on the global change of coordinates. E and Engquist [35,36] proposed the heterogeneous multiscale method (HMM) that was later developed in ﬁnite-difference and ﬁnite-element formulations [41,42,1]. The HMM also requires evaluations of local problem in each time step, which is expensive. Capdeville et al. [11] proposed a numerical homogenization method for non-periodic heterogeneous elastic media, which extracts the microscopic part of medium properties, followed by a homogenization expansion. However, this method assumes scale separation of the media, which cannot always be satisﬁed in practice. Based on previous work for the elliptic partial differential equations, the acoustic wave equation and the isotropic lin- ear elasticity equation [39,37,38,17,21,48,18], we propose a GMsFEM to simulate the wave propagation in heterogeneous, anisotropic elastic media on the coarse mesh. The essence of our GMsFEM is to construct multiscale basis functions with ap- propriately deﬁned local problems, which will be used in both CG and DG formulations of the GMsFEM. We investigated two types of related yet different multiscale basis functions for GMsFEM. For the ﬁrst type of multiscale basis function, we solve a linear elasticity eigenvalue problem in the support of a node on the coarse mesh, or in the region of a coarse element. By selecting the eigenfunctions correspond to the ﬁrst several smallest eigenvalues, we construct a ﬁnite-dimensional basis function space for GMsFEM. For the second type of multiscale basis function, we construct a basis space which is composed of two orthogonal subspaces, and these two subspaces consist of multiscale functions deﬁned with different local spectral problems. The ﬁrst subspace is spanned by the basis functions that are solved directly from the local eigenvalue problem of linear elasticity for the interior nodes of the coarse node support or coarse element, while the second subspace consists of the basis functions solved from a local spectral problem which is related to the boundaries of the coarse node support or the coarse element in GMsFEM. For both of these spaces, we select the eigenfunctions that correspond to the ﬁrst several smallest eigenvalues. These basis functions correspond to the local eigenmodes with lowest frequencies. The resulting GMs- FEM allows us to utilize these multiscale basis functions to capture the ﬁne scale information of the heterogeneous media, while effectively reducing the degrees of freedom that are required to implement the modeling compared with conventional method such like CG- and DG-FEM. Our paper is organized as follows. We ﬁrst introduce the CG and DG formulations of GMsFEM for the elastic wave equa- tion in heterogeneous, anisotropic media. Speciﬁcally, we deﬁne the appropriate bilinear forms for the elastic wave equation, then we introduce two approaches to construct the multiscale basis functions with appropriately deﬁned local problems, as well as the oversampling technique to reduce the inﬂuence of prescribed boundary conditions, and an adaptive way to assign different numbers of basis functions for coarse elements in DG-GMsFEM. We then present three numerical results to verify the effectiveness of our multiscale method, including a heterogeneous model composed of vertical transversely isotropic (VTI), tilted transversely isotropic (TTI) and isotropic layers, a heterogeneous model composed of curved layers and random heterogeneities. The last numerical example is devoted to verify the adaptive assignment of number of basis functions. Finally, we give a brief discussion of limitations of our current work and propose some possible improvements. 2. Theory We will develop both the CG- and DG-GMsFEM in this section. We will ﬁrst give the weak forms of the elastic wave equation in CG and DG formulations, then we will show how to construct the multiscale basis functions using appropriately deﬁned local spectral problems. Although the formulations of CG- and DG-GMsFEM are different, the multiscale basis func- tions for these two formulations can be constructed in the same way. In other words, the construction of the multiscale basis functions is independent of the CG or DG formulations for the elastic wave equation. In fact, we will see that the construction of the multiscale basis function is only related to the spatial part of the elastic wave equation. We remark that we present the deﬁnitions, equations and derivations in this part in a general style, and therefore they are valid for both 2D and 3D cases. However, we will present only 2D examples in this part, as well as the next part of numerical results. 2.1. Weak form of the elastic wave equation We begin with the elastic wave equation in the form (e.g., [12]) ρ∂ 2.1.1. Elastic wave equation t u = ∇ · σ + f, σ = c : ε, ε = 1 2 (1a) (1b) 2 [∇u + (∇u) T] (1c) where u = u(x, t) is the displacement waveﬁeld we aim to solve with our multiscale method in the spatial domain , which could be 2D or 3D in general, and the temporal domain [0, T]. Also σ = σ (u) is the stress tensor, ε = ε(u) is the strain tensor, f is the external source term, c = c(x) = cijkl(x) is the fourth-order elasticity tensor where i, j, k, l = 1, 2, 3 [12] and ρ = ρ(x) is the density of the medium. In our approach, the elasticity tensor c can be generally anisotropic, i.e., all the 21 independent elasticity parameters in c can be non-zero in the 3D case. However, since we will present only 2D results in this paper, we only consider the elasticity

164 K. Gao et al. / Journal of Computational Physics 295 (2015) 161–188 Fig. 1. A sketch of the ﬁne mesh Th, denoted by gray mesh, and coarse mesh TH , denoted by black mesh, in CG formulation of GMsFEM. Gray rectangle labeled K represents the support of the i-th coarse node. K contains many ﬁner element, which might have high contrasts in medium properties. tensor with i, j, k, l = 1, 3. Therefore, with Voigt notation (e.g., [12]), we can express the elasticity tensor c in the following matrix form: ⎛ ⎝ C11 C13 C15 C13 C33 C35 C15 C35 C55 ⎞ ⎠ , C = (2) (4) (5) which can describe the elastic wave propagation in anisotropic media with symmetry up to hexagonal anisotropy with tilted symmetry axis in the x1–x3 plane (transversely isotropy with tilted axis, TTI), and monoclinic anisotropy (assuming the symmetry plane is the x1–x3 plane), where C15 and C35 are possibly non-zero. 2.1.2. CG formulation We ﬁrst formulate the multiscale method in the CG framework for 2D elastic waveﬁeld simulations with applications to higher-order cases of anisotropy. For the CG formulation, we ﬁrst discretize the whole computational domain with a coarse mesh TH overlying a ﬁner mesh Th. Fig. 1 illustrates this mesh design, where we use the black lines to represent the coarse mesh, and gray lines to represent the ﬁner mesh. The support of a coarse node can be denoted as K , which contains many ﬁner elements. The mesh can be unstructured, though we assume structured elements in the theory development to develop the current results. Nevertheless, the following derivations are equally valid for an unstructured mesh. We express the displacement waveﬁeld u on the coarse mesh TH as di(t)i(x), (3) where i(x) are the spatial basis functions of uH (x, t), and i belong to the ﬁnite-dimensional function space V H = {i}N i=1. Note that each i is piecewise continuous in . Space V H is our multiscale basis function space, which will be deﬁned in the next section. We multiply the elastic wave equation (1) with a test function v ∈ V H , integrate over , apply Gauss’s theorem, and get the weak form of the elastic wave equation as uH (x, t) = N i=1 t uH · vdx + aCG(uH , v) = 2 ρ∂ f · vdx, where the bilinear form aCG is aCG(u, v) = σ (u) : ε(v)dx + [σ (u) · n] · vds. ∂ Also, n is the outward pointed normal of ∂. We have set homogeneous Neumann boundary condition, i.e., σ (u) · n = 0, for simplicity. 2.1.3. DG formulation The discontinuous Galerkin formulation of our multiscale method is a natural choice if a non-conformal mesh is taken into consideration. For DG formulation, we discretize with a set of coarse mesh cells PH , each coarse element containing

K. Gao et al. / Journal of Computational Physics 295 (2015) 161–188 165 uH (x, t) = N Fig. 2. A sketch of the ﬁne mesh Ph, denoted by gray mesh, and coarse mesh PH , denoted by black mesh in DG formulation of GMsFEM. Gray rectangle labeled K represents the i-th coarse element. Same with that in CG-GMsFEM, coarse block K contains many ﬁner elements which might have high contrasts in medium properties. more ﬁnely discretized elements in the ﬁner mesh Ph, as is shown in Fig. 2 for a 2D meshing case. Again, the solution of the wave equation (1) can be expressed as i=1 di(t)i(x), (6) where the basis functions i ∈ W H . The multiscale basis function space W H will be deﬁned in the next section. We assume that the basis functions i are continuous within each coarse element K , but generally discontinuous at the coarse element boundaries ∂ K . As is true in general for discontinuous Galerkin ﬁnite-element methods (e.g., [51,5,102]), we deﬁne some terms related to the boundaries of the coarse element. Letting EH be the set of all interior coarse element edges in the 2D case (the set of all interior coarse element faces in 3D), then we deﬁne the average of a tensor σ on E ∈ EH as (σ {{σ}} = 1 2 + + σ − ± = σ|K± , and K where σ E ∈ EH is given by: + − v [[v]] = v − ), (7) ± are the two coarse elements having the common E. Meanwhile, the jump of a vector v on (8) We also have a matrix jump term resulting from the outer product of a vector with edge or face normals, which is deﬁned as , [[v]] = v + ⊗ n + + v − ⊗ n − , where n± is the unit outward normal vector on the boundary of K boundary ∂, the above average and jump terms can be deﬁned as (9) ±. In addition, for the edges on the computation domain [[v]] = v, {{σ}} = σ , We multiply the elastic wave equation (1) with some arbitrary test function v ∈ W H , and get the weak form where n is the outward pointed normal of coarse element K . [[v]] = v ⊗ n, t uH · vdx + aDG(uH , v) = 2 ρ∂ where the bilinear form aDG(u, v) is deﬁned as aDG(u, v) = f · vdx, E∈EH E K∈PH + E∈EH K σ (u) : ε(v)dx − γ|E| E ({{σ (u)}} : [[v]] + η[[u]] : {{σ (v)}})ds ([[u]] : {{c}} : [[v]] + [[u]] · {{D}} · [[v]])ds, with D = diag(C11, C22, C33), C I J are components of the fourth-order elasticity tensor c in Voigt notation (e.g., [12]). η is a parameter that takes values −1, 0 or 1, and we choose η = 1, which makes our method the classical symmetric interior (10) (11) (12)

166 K. Gao et al. / Journal of Computational Physics 295 (2015) 161–188 penalty Galerkin (SIPG) method [5,21,29]. γ is the penalty parameter, and we set γ > 0. We have omitted the terms re- lated to the boundary edges, since we assume a homogeneous Neumann boundary condition. This bilinear form is inspired by those deﬁned for linear elasticity problem [102] and isotropic elastic wave equation [29], however, we have used non- constant matrix penalty parameters and two different penalty terms, i.e., { {c} } = { {c(x)} } and { {D} } = { {D(x)} }. We ﬁnd that such penalty terms can better guarantee the stability of the DG scheme. Meanwhile, we use a ﬁxed γ for all boundaries for convenience, which can alternatively vary from edge to edge. It should be remarked that the bilinear form (12), which is essentially the time-independent part of the elastic wave equation (1), is not unique, and there are some other similar choices which may be equally good (e.g., [86,60,53]). 2.2. Multiscale basis functions The key task in our multiscale method, given the choice of one of the above weak forms of the elastic wave equa- tion, is to construct appropriate multiscale basis functions i or i to form the function space V H or W H for CG- or DG-GMsFEM. In this section, we will introduce two methods to construct the multiscale basis functions, both are solved from appropriately deﬁned local problems, and both can be taken to form the basis function space for the wave equation. We note that the same basis functions are used for both the CG- and the DG-GMsFEM simulations and the selection of basis functions is therefore independent of the coarse scale formulation. 2.2.1. Type I The ﬁrst way to deﬁne a set of multiscale basis functions for GMsFEM is solving a local linear elasticity eigenvalue problem. Speciﬁcally, suppose K is the support of a coarse node in CG formulation, or the coarse element in DG formulation, then we solve the following eigenvalue problem in K : (13c) with zero Neumann boundary condition σ · n = 0 on ∂ K , where ζ is the eigenvalue, and n is the outward pointed normal of K . The elasticity tensor c can be spatially heterogeneous. This local problem corresponds to the following discrete system: where the global stiffness and global mass matrices A and M are computed from (13a) (13b) (14) (15) (16) (17) (18) −∇ · σ = ζ ρu, σ = c : ε, ε = 1 2 [∇u + (∇u) T], AU = ζ MU, A = M = σ (γ ) : ε(η)dx, ργ · ηdx, K K for the coarse node support or coarse element K , with γ , η ∈ V h, and they can be discretized and calculated with appro- priate quadrature and integration rules [57,7] for calculation of eigenvectors. The above linear elasticity eigenvalue problem can be solved with a conventional solver without diﬃculties, since nor- mally the dimension of the above system is not large due to the limited size of a coarse element. To ensure stability, we can add to A a value 10−8 to 10−9 times the maximum on the diagonal of A. Solutions of the eigenvalue problem for the dis- modes in K with frequencies ωk = √ placement u are labeled as ψk, denoting the k-th eigen-displacement in the coarse block K . Physically, they are the standing ζk. Depending on the dimension of the coarse block K , there can be many eigenfunctions associated with the local prob- lem (13). The analyses for elliptic partial differential equation [37] and for acoustic wave equation [17,21,45] indicate that it is adequate to select only a few of the eigenfunctions as the basis functions for uH . The criterion for selecting eigen- functions is to chose those representing most of the energy in the eigenmodes ψk. Correspondingly, the sum of the inverse of selected eigenvalues (L is the number of eigenfunctions). We can select the ﬁrst m eigenfunctions ψ 1, ψ 2, ···, ψm corresponding to the m small- est eigenvalues 0 ≤ ζ1 ≤ ζ2 ≤ ··· ≤ ζm of the above local problem, and construct the multiscale basis function space for DG-GMsFEM as should be a large portion of the sum of all the inverse of eigenvalues −1 L l=1 ζ l −1 m l=1 ζ l W H (K ) = span{ψ 1, ψ 2,··· , ψm}. For CG-GMsFEM, the basis functions space can be constructed from the ﬁrst m eigenfunctions as V H (K ) = span{χ K ψ 1, χ K ψ 2,··· , χ K ψm},

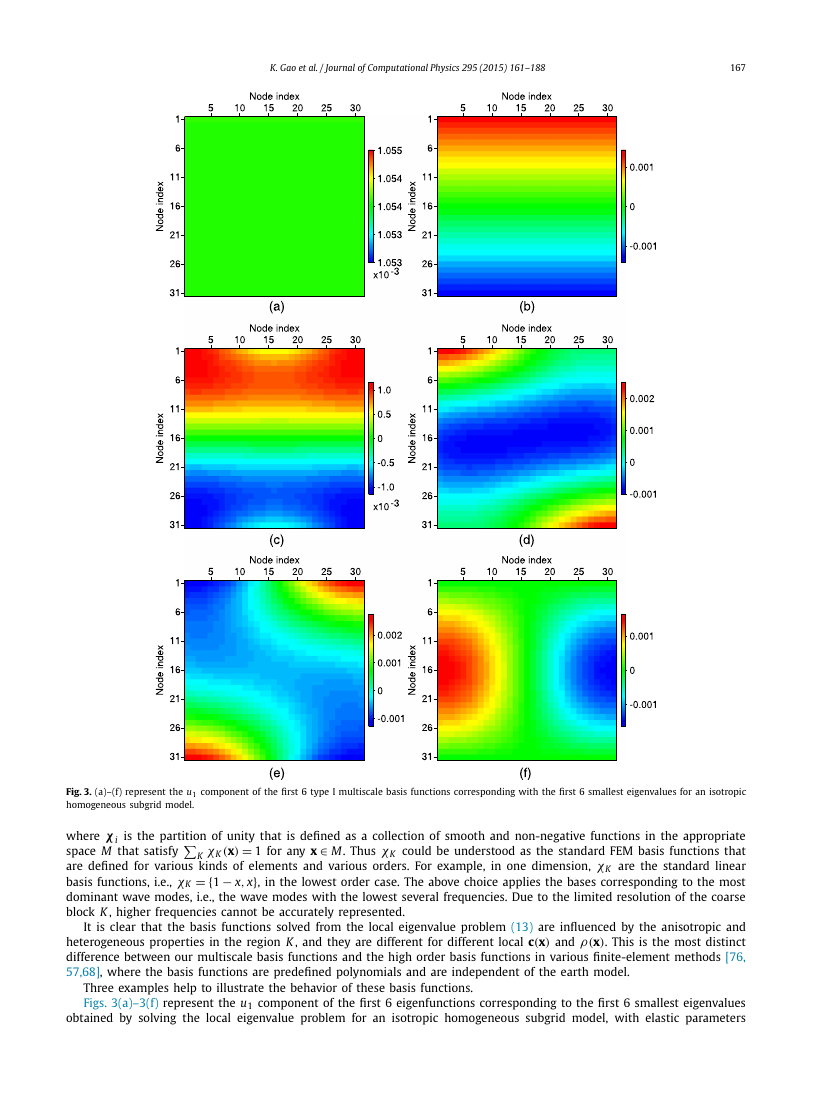
K. Gao et al. / Journal of Computational Physics 295 (2015) 161–188 167 Fig. 3. (a)–(f) represent the u1 component of the ﬁrst 6 type I multiscale basis functions corresponding with the ﬁrst 6 smallest eigenvalues for an isotropic homogeneous subgrid model. where χ i is the partition of unity that is deﬁned as a collection of smooth and non-negative functions in the appropriate K χK (x) = 1 for any x ∈ M. Thus χK could be understood as the standard FEM basis functions that space M that satisfy are deﬁned for various kinds of elements and various orders. For example, in one dimension, χK are the standard linear basis functions, i.e., χK = {1 − x, x}, in the lowest order case. The above choice applies the bases corresponding to the most dominant wave modes, i.e., the wave modes with the lowest several frequencies. Due to the limited resolution of the coarse block K , higher frequencies cannot be accurately represented. It is clear that the basis functions solved from the local eigenvalue problem (13) are inﬂuenced by the anisotropic and heterogeneous properties in the region K , and they are different for different local c(x) and ρ(x). This is the most distinct difference between our multiscale basis functions and the high order basis functions in various ﬁnite-element methods [76, 57,68], where the basis functions are predeﬁned polynomials and are independent of the earth model. Three examples help to illustrate the behavior of these basis functions. Figs. 3(a)–3(f) represent the u1 component of the ﬁrst 6 eigenfunctions corresponding to the ﬁrst 6 smallest eigenvalues obtained by solving the local eigenvalue problem for an isotropic homogeneous subgrid model, with elastic parameters

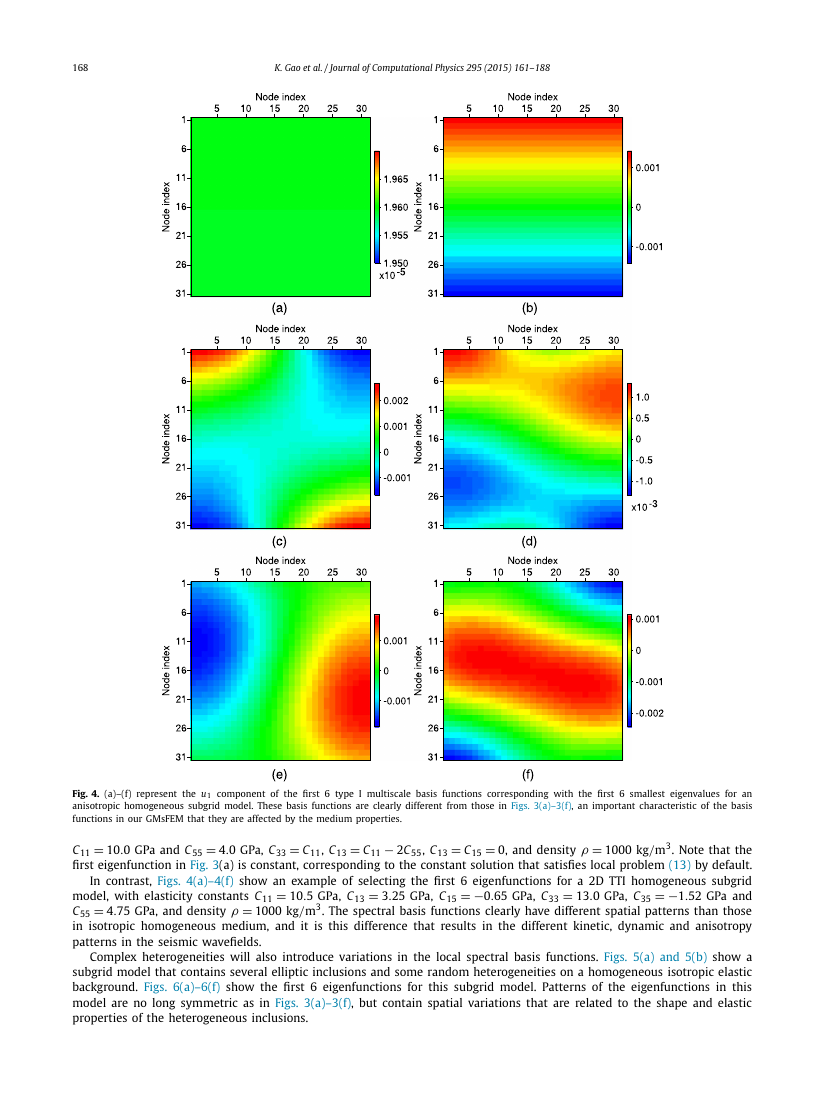
168 K. Gao et al. / Journal of Computational Physics 295 (2015) 161–188 Fig. 4. (a)–(f) represent the u1 component of the ﬁrst 6 type I multiscale basis functions corresponding with the ﬁrst 6 smallest eigenvalues for an anisotropic homogeneous subgrid model. These basis functions are clearly different from those in Figs. 3(a)–3(f), an important characteristic of the basis functions in our GMsFEM that they are affected by the medium properties. C11 = 10.0 GPa and C55 = 4.0 GPa, C33 = C11, C13 = C11 − 2C55, C13 = C15 = 0, and density ρ = 1000 kg/m3. Note that the ﬁrst eigenfunction in Fig. 3(a) is constant, corresponding to the constant solution that satisﬁes local problem (13) by default. In contrast, Figs. 4(a)–4(f) show an example of selecting the ﬁrst 6 eigenfunctions for a 2D TTI homogeneous subgrid model, with elasticity constants C11 = 10.5 GPa, C13 = 3.25 GPa, C15 = −0.65 GPa, C33 = 13.0 GPa, C35 = −1.52 GPa and C55 = 4.75 GPa, and density ρ = 1000 kg/m3. The spectral basis functions clearly have different spatial patterns than those in isotropic homogeneous medium, and it is this difference that results in the different kinetic, dynamic and anisotropy patterns in the seismic waveﬁelds. Complex heterogeneities will also introduce variations in the local spectral basis functions. Figs. 5(a) and 5(b) show a subgrid model that contains several elliptic inclusions and some random heterogeneities on a homogeneous isotropic elastic background. Figs. 6(a)–6(f) show the ﬁrst 6 eigenfunctions for this subgrid model. Patterns of the eigenfunctions in this model are no long symmetric as in Figs. 3(a)–3(f), but contain spatial variations that are related to the shape and elastic properties of the heterogeneous inclusions.

分享到：

赞收藏

资料库

最全的有限元介绍.pdf

相关推荐

信息化

热门标签

最新资料