logo资料库

自动控制原理课程设计--用MATLAB进行控制系统的滞后校正设计.docx

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.22M 资料格式：docx 举报 版权申诉
第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
资料共11页，剩余部分请下载后查看
    4.系统校正前后根轨迹图
    4.1未校正系统根轨迹图
    4.2校正后系统根轨迹图
    5.心得体会
    参考文献
    武汉理工大学《自动控制原理》课程设计说明书 1 滞后校正特性及校正方法 1.1 滞后校正特性 滞后校正就是在前向通道中串联传递函数为 )(sGc 的校正装置来校正控制系统， )(sGc 的表达式如下所示。 sGc 1)( aTs   1 Ts  , a  1 (1.1-1) 其中，参数 a、T 可调。滞后校正的高频段是负增益，因此，滞后校正对系统中高频噪声 有削弱作用，增强了抗干扰能力。可以利用滞后校正的这一低通滤波所造成的高频衰减特 性，降低系统的截止频率，提高系统的相位裕度，以改善系统的暂态性能。 滞后校正的基本原理是利用滞后网络的高频幅值衰减特性使系统截止频率下降，从而 使系统获得足够的相位裕度。或者，是利用滞后网络的低通滤波特性，使低频信号有较高 的增益，从而提高了系统的稳态精度。 可以说，滞后校正在保持暂态性能不变的基础上，提高开环增益。也可以等价地说滞 后校正可以补偿因开环增益提高而发生的暂态性能的变化。 1.2 滞后校正设计的一般步骤与方法 （1）按稳态性能指标要求的开环放大系数绘制未校正系统的伯德图。 如果未校正系统需要补偿的相角较大，或者在截止频率附近相角变化大，具有这样特 性的系统一般可以考虑用滞后校正。 （2）在未校正系统的伯德图上找出相角为 - （ 180  ） 的频率作为校正后系统的截止 频率 ' cw ，其中为要求的相位裕度，为补偿滞后校正在 '  10~5  。 cw 产生的相位滞后，一般取 的选取：是为了补偿滞后校正的相位滞后的，一般限制滞后校正的滞后相角小于 10 ，所以可以取小于 10 的值。应取一个尽量小，但又能补偿滞后校正在 ' cw 小，则取大一些。 角的值。一般，若 ' cw 较大，可取小一些。反之，若 ' cw 处的滞后相 （3）在未校正系统的伯德图上量取量取 ）（ ' cwL 0 （或由 lg20 | ' jwG c ( 0 |) 求取）的分贝值， 并令 lg20 | ' jwG c ( 0 |)  这一步的意思是，在 ，由此确定参数 a(a<1)。 1lg20 a cww  处，设计滞后校正的幅值与原系统的幅值反向相等才能相 ' 1
    武汉理工大学《自动控制原理》课程设计说明书 互抵消，使校正后系统的截止频率为 ' cw 。 （4）取 1 aT  1( 5 1~ 10 ) ' cw ，并由 a 求参数 T。 选 1 的 原 则 是 使 aT arctanw |)  arctanaw  ' T c ' T c |  c (w ' c ( c w c ) 不 超 过 （ 2 ） 中 所 选 的  值 ， 即   。校正时只需要近似值， 1 可近似由下式选取。 aT 1 aT  ' w c cot( 90  )   ' w c tan  (1.2-1) （5）绘制校正后系统的伯德图，校验各项性能指标，若不满足，可重新选择 ' cw 或 1 aT 的值。 2
    武汉理工大学《自动控制原理》课程设计说明书 2 校正前系统的分析 2.1 校正前参数确定 2.1.1 确定校正前单位反馈系统的开环增益 K 单位反馈系统的开环传递函数是： )( sG  s K s )2.01)(1.01( s   要求系统的静态速度误差系数 K v  100  S 1 ，利用误差系数法确定系统的开环增益 K， 计算如下。 1  ）（ S   sHs K   1s2.01   KV   lim s 0  100 sG   lim  0.1s s 0  100 K  因而校正前系统的开环传递函数为   SG  s 100  s  2.011.01   。 s 2.1.2 确定校正前单位反馈系统的幅值裕度和相位裕度 先求校正前系统的幅值裕度。 令 ）（w  180  相位截止频率 gw 。 ）（ 90 w 1  tg 1.0 tgw  1  2.0 w ) ( wA  100 04.01  2 w  1 w 01.0 w 2 (2.1-1) (2.1-2) 可以确定幅值裕度对应的相位截止频率 gw 。利用三角函数可以求出 1  tg 1.0 tgw  1  2.0 tgw  1  3.0 w 02.01 w  2  0 gw  90  2 02.01  因而解得 gw =7.07rad/s。 ) ( wA g  04.01 w ( gwA 可以方便地求出幅值裕度 gK 或者 h。 01.0 w w ) g 2 g 利用 100   67.6 2 g  1 K g  h  1 ) ( wA g lg20 K  1 67.6  5.16 dB  15.0 g 3
    武汉理工大学《自动控制原理》课程设计说明书 求校正前系统的相位裕度。 先求增益穿越频率 cw 。在增益穿越频率 cw 处，系统的开环频率特性的幅值为 1。 ( wA c )  w c 2 01.0 w c 100  04.01  2.0 2 w c 2 w c  1  1 100 2 01.0 w c ）（ cw 。 1  由上式求得 wc 7.16 rad / 。利用增益穿越频率 cw 可以计算 s 90 w ）（  2.0  tg tg 1.0 w c w c  1  1  c 4.222  由 ）（ cw 的值可以确定相角裕度。 ）（ cw  180    180  4.222  4.42  2.2 用 MATLAB 作出系统校正前的伯德图，并计算系统校正前的幅值裕度 和相位裕度。 绘制校正前系统的伯德图的 MATLAB 程序，并由 MATLAB 计算系统校正前的幅值裕度和 相位裕度，程序如下: num=100 den=[0.02,0.3,1,0] g1=tf(num,den) [mag,phase,w]=bode(g1)；%绘制g1的幅频特性和相频特性曲线 margin(g1) MATLAB得出的结果如下: num = 100 den = 0.0200 0.3000 1.0000 0 Transfer function: 100 ---------------------- 0.02 s^3 + 0.3 s^2 + s 4
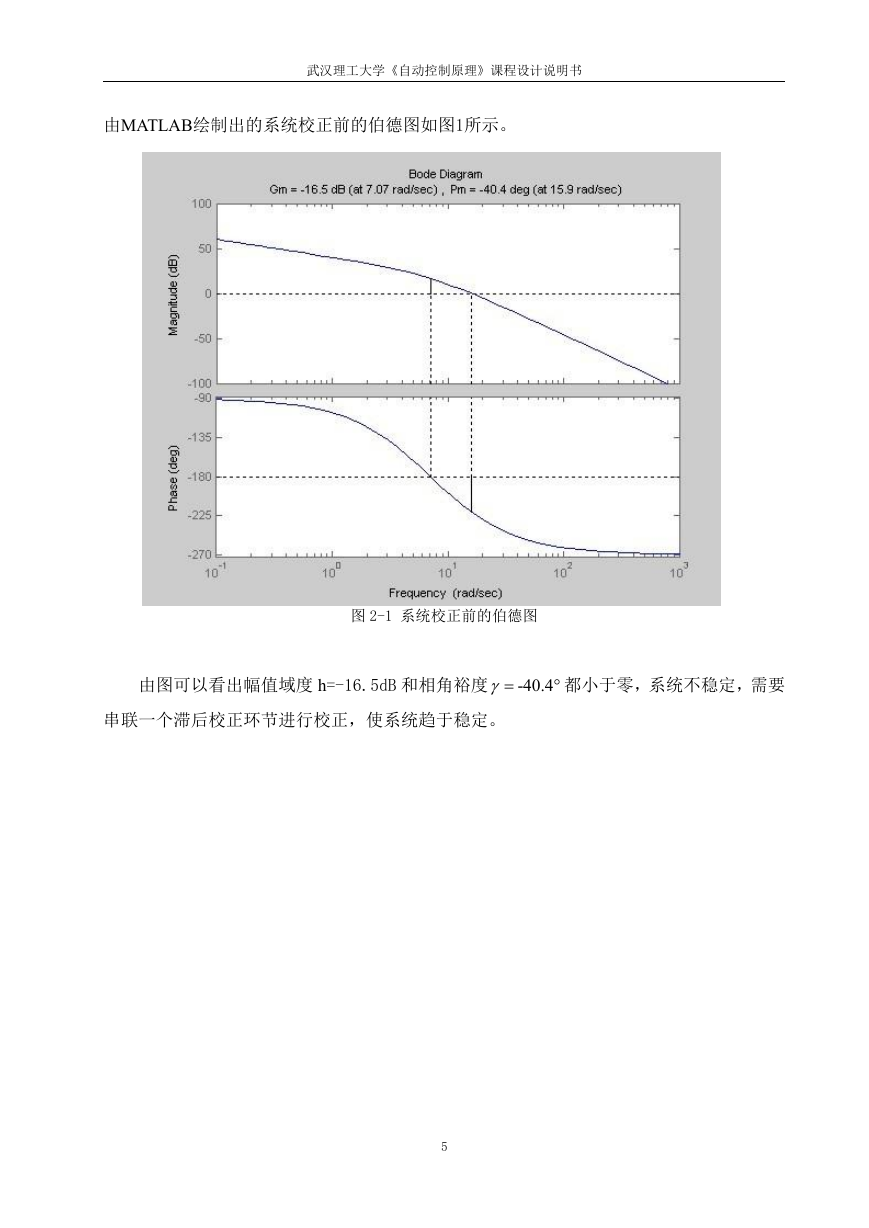
    武汉理工大学《自动控制原理》课程设计说明书 由MATLAB绘制出的系统校正前的伯德图如图1所示。 图 1 校正前系统的伯德图 图 2-1 系统校正前的伯德图 由图可以看出幅值域度 h=-16.5dB 和相角裕度 4.40-   都小于零，系统不稳定，需要 串联一个滞后校正环节进行校正，使系统趋于稳定。 5
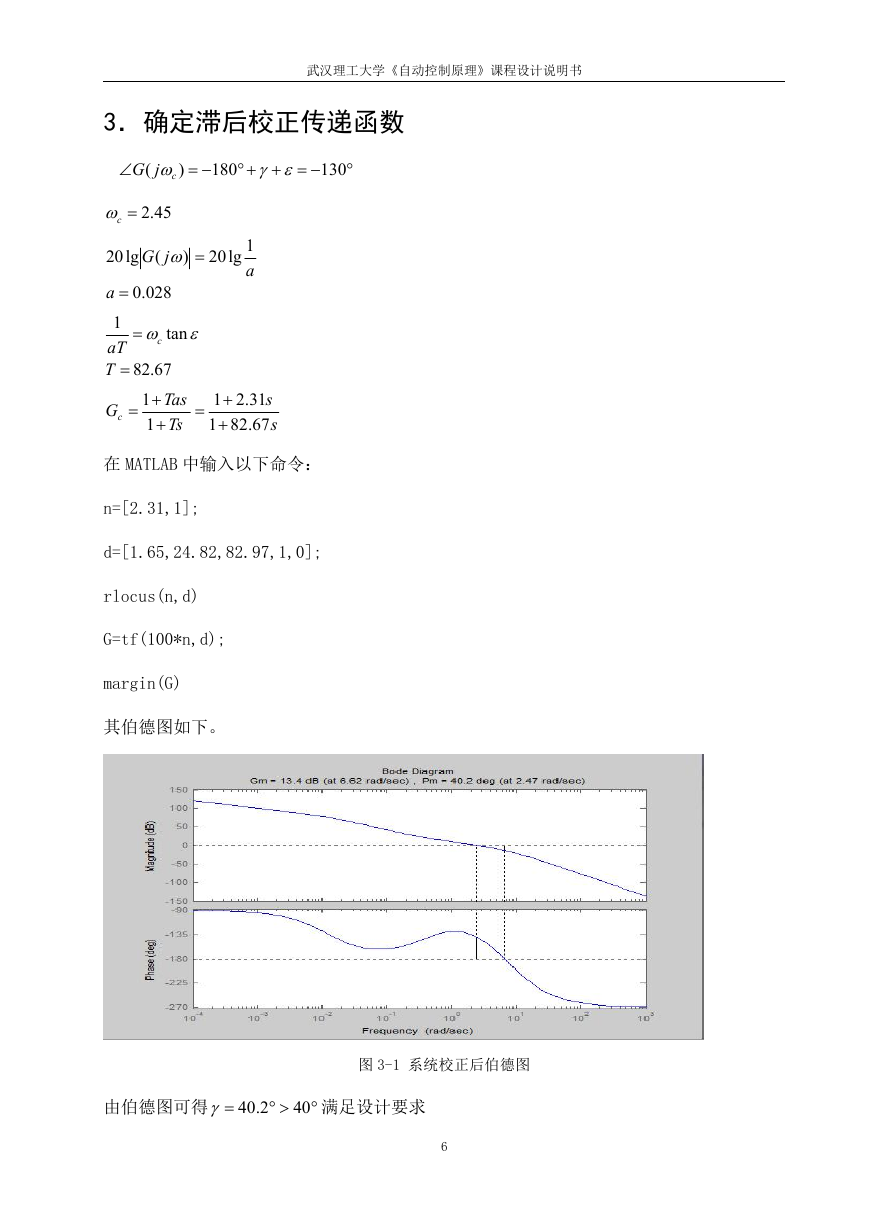
    武汉理工大学《自动控制原理》课程设计说明书 3．确定滞后校正传递函数  ( jG c )  180   130  45.2c lg20 ) jG  (  a  1 aT T  Gc  .0 028  tan c  67.82 1 Tas  1 Ts   1lg20 a 31.21 s  67.82 1 s  在 MATLAB 中输入以下命令： n=[2.31,1]; d=[1.65,24.82,82.97,1,0]; rlocus(n,d) G=tf(100*n,d); margin(G) 其伯德图如下。 图 3-1 系统校正后伯德图 由伯德图可得 2.40   40  满足设计要求 6
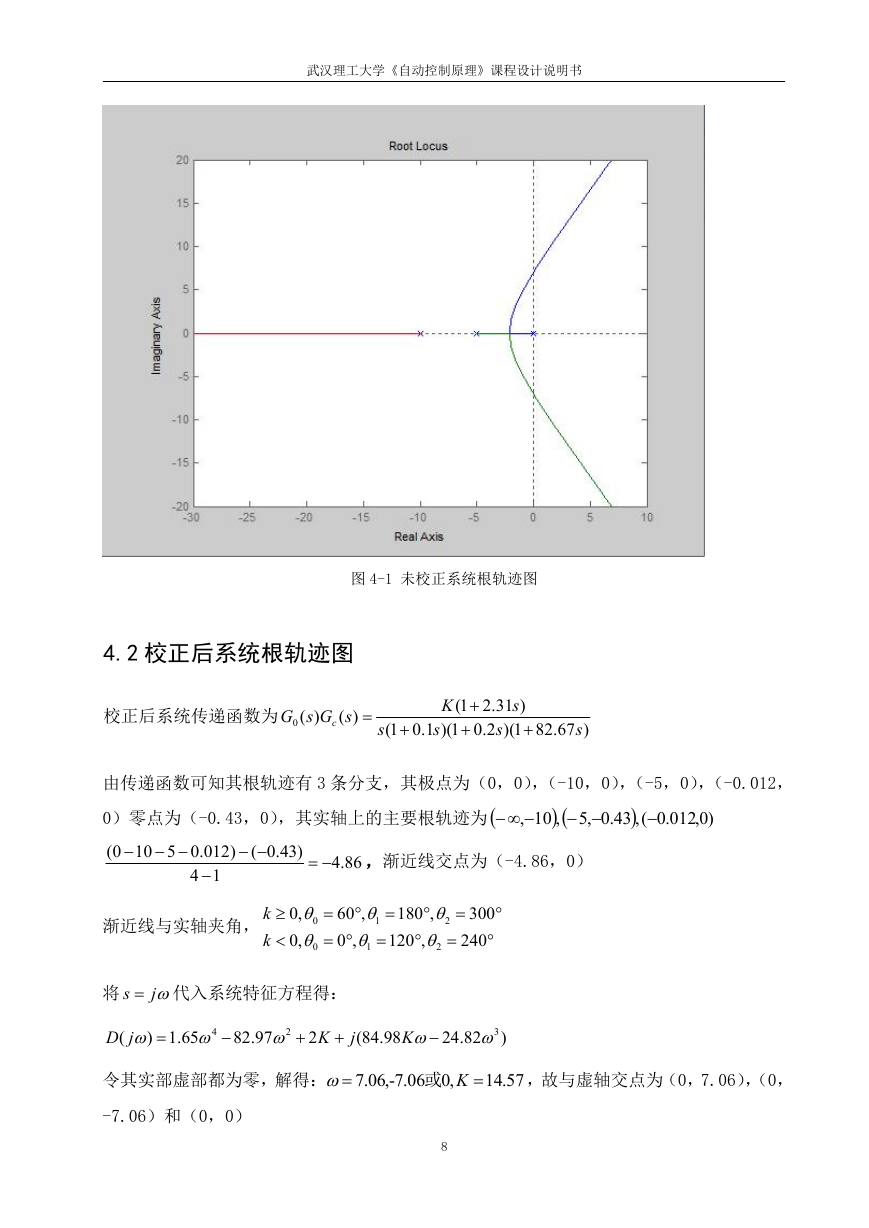
    武汉理工大学《自动控制原理》课程设计说明书 4.系统校正前后根轨迹图 4.1 未校正系统根轨迹图 系统校正前传递函数为： )(0 sG  s K s )2.01)(1.01( s   由传递函数可知其根轨迹有 3 条分支，其极点为（0，0），（-10，0），（-5，0），没有零点， 其实轴上的主要根轨迹为 0   ,10  ,  0,5 5 10   03  5  ，渐近线交点为（-5，0） 渐近线与实轴夹角， k k   ,0 ,0  0  0 , ,60 180 300        1 2 ,0 , 120 240        1 2  将 j s  代入系统特征方程得： ( jD )   K  3.0 2    j ( 02.0 3  ) 令其实部为零，解得： 0,07.7-,07.7 ，K=15，故与虚轴交点为（0，7.07），（0，-7.07） 和（0，0） 1 d  1  5 d  d 1 10   0 解得： d 1  ,11.2 d 2  89.7 （舍去） 在 matlab 的命令窗口中输入的程序为： n=1; d=[0.02,0.3,1,0]; rlocus(n,d) 7
    武汉理工大学《自动控制原理》课程设计说明书 图 4-1 未校正系统根轨迹图 4.2 校正后系统根轨迹图 校正后系统传递函数为 )(0 )( sGsG c  s K )31.21( s  1)(2.01)(1.01(    s s )67.82 s 由传递函数可知其根轨迹有 3 条分支，其极点为（0，0），（-10，0），（-5，0），（-0.012， 0）零点为（-0.43，0），其实轴上的主要根轨迹为 0( )0,012.0(,43.0,5    ,10  )43.0( ,   10    ) 012.05 14   86.4 ，渐近线交点为（-4.86，0） 渐近线与实轴夹角， k k   ,0 ,0  0  0 , ,60 180 300        1 2 ,0 , 120 240        1 2  将 j s  代入系统特征方程得： ( jD  65.1)  4   97.82 2   2 jK  98.84( K   82.24 3  ) 令其实部虚部都为零，解得：   -7.06）和（0，0） 06.7-,06.7 K或 ,0  57.14 ，故与虚轴交点为（0，7.06），（0， 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料