vc实现圆的生成算法实验报告.doc

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.20M 资料格式：doc 举报版权申诉

CAO060806110019-1237386-4744302543397404438.doc.pdf-第1页.png

第1页 / 共11页

CAO060806110019-1237386-4744302543397404438.doc.pdf-第2页.png

第2页 / 共11页

CAO060806110019-1237386-4744302543397404438.doc.pdf-第3页.png

第3页 / 共11页

CAO060806110019-1237386-4744302543397404438.doc.pdf-第4页.png

第4页 / 共11页

CAO060806110019-1237386-4744302543397404438.doc.pdf-第5页.png

第5页 / 共11页

CAO060806110019-1237386-4744302543397404438.doc.pdf-第6页.png

第6页 / 共11页

CAO060806110019-1237386-4744302543397404438.doc.pdf-第7页.png

第7页 / 共11页

CAO060806110019-1237386-4744302543397404438.doc.pdf-第8页.png

第8页 / 共11页

文本预览

贵州大学实验报告学院：计算机科学与技术专业：计算机科学与技术班级： 0 6 计科 1 班姓名曹杰先学号 060806110019 实验组实验时间 2009-3-30 指导教师成绩实验项目名称圆的生成算法实 1、通过实验，进一步理解和掌握中点算法、Bresenham 算法和二阶差分算法；验 2、掌握以上算法生成圆的基本过程；目 3、通过编程，学习 VC 环境下完成用中点算法、Bresenham 算法和二阶差分算法实现圆的绘的制。实验 1、在 VC 环境下利用 MFC 编程实现分别利用中点算法、Bresenham 算法和二阶差分算法实现圆的绘制。要 2、给出代码。求 3、附上结果截图。 A：算法原理 1、圆的特征--八分对称性实验原理圆被定义为到给定中心位置（xc,yc）距离为 r 的点集。圆心位于原点的圆有四条对称轴 x=0,y=0, x=y 和 x=-y。若已知圆弧上一点（x,y）,可以得到其关于四条对称轴的其它 7 个点，这种性质称为八分对称性。因此，只要扫描转换八分之一圆弧，就可以求出整个圆弧的象素集。 2、中点画圆法构造圆函数。对于圆上的点，；对于圆外的

点；对于圆内的点。与中点画线法一样，构造判别式若则应取 P1 为下一象素，而且再下一象素的判别式为若则应取 P2 为下一象素，而且下一象素的判别式为 3、Bresenham 算法的基本原理假定直线斜率|k|≤1 。此时，只需考虑 x 方向每次递增 1 个单位，决定 y 方向每次递增 0 或 1。设直线的当前点为(xi，y)当前光栅点为(xi，yi)下一个直线的点应为(xi+1，y+k) 相应的光栅点或为右光栅点(xi+1，yi) （y 方向递增量 0）或为右上光栅点(xi+1， yi+1)（y 方向递增量 1）记直线与它垂直方向最近的下光栅点的误差为 d，有： 0≤d≤1 当 d<0.5：下一个象素应取右光栅点(xi+1，yi)当 d≥0.5：下一个象素应取右上光栅点(xi+1，yi+1)如果直线的（起）端点在整数点上，误差项 d 的初值： d0＝0 x 坐标每增加 1，d 的值相应递增直线的斜率值 k，即：d＝d+k 一旦 d≥1，就把它减去 1，保证 d 的相对性，即在 0-1 之间。令 e=d-0.5，关于 d 的判别式和初值可简化成： e 的初值 e0= -0.5，增量亦为 k;

e<0 时，取当前象素(xi,yi)的右方象素(xi+1，yi)； e>0 时，取当前象素(xi,yi)的右上方象素(xi+1，yi+1)； e=0 时，可任取上、下光栅点显示。因为 e 是相对量，所以当 e>0 时，表明 e 的计值将进入下一个参考点（上升一个光栅点），此时须：e = e – 1 B 核心代码如下：  Bresenham void CCircleView::Mbcircle() { double x,y,d; d=1.25-R;x=0;y=R; for(x=0;x

d=1.25-R;x=0;y=R; CirclePoint(x, y); while (y>x) { if (d<0) d+=2.0*x+3.0; else { } d+=2.0*(x-y)+5.0; y--; x++; CirclePoint(x, y); } }  二阶差分算法 void CCircleView::Erjie() { int x,y,d; d=int(1-R);x=0;y=int(R); CirclePoint(x,y); while (y>x) { if (d<0) d+=2*x+3; else { d+=2*(x-y)+5;

y--; } x++; CirclePoint(x,y); } } void CCircleView::GetMaxY() { } CRect Rect; GetClientRect(&Rect); MaxY=Rect.bottom; void CCircleView::GetMaxX() CRect Rect; GetClientRect(&Rect); MaxX=Rect.right; { } void CCircleView::CirclePoint(double x, double y) { CClientDC dc(this); COLORREF rgb=RGB(255,128,255); dc.SetPixel(ROUND(x)+MaxX/2,ROUND(y)+MaxY/2,rgb);//x,y dc.SetPixel(ROUND(y)+MaxX/2,ROUND(x)+MaxY/2,rgb);//y,x dc.SetPixel(-ROUND(y)+MaxX/2,ROUND(x)+MaxY/2,rgb);//y,-x

dc.SetPixel(ROUND(x)+MaxX/2,-ROUND(y)+MaxY/2,rgb);//x,-y dc.SetPixel(-ROUND(x)+MaxX/2,-ROUND(y)+MaxY/2,rgb);//-x,-y dc.SetPixel(-ROUND(y)+MaxX/2,-ROUND(x)+MaxY/2,rgb);//-y,x dc.SetPixel(ROUND(y)+MaxX/2,-ROUND(x)+MaxY/2,rgb);//-y,-x dc.SetPixel(-ROUND(x)+MaxX/2,ROUND(y)+MaxY/2,rgb);//x,y } void CCircleView::OnMENUCie() { } // TODO: Add your command handler code here CircleDlg dlg; if(dlg.DoModal()==IDOK) { } R=dlg.m_R; AfxGetMainWnd()->SetWindowText("Bressenham 算法"); RedrawWindow(); GetMaxX(); GetMaxY(); Mbcircle(); void CCircleView::OnMENUMid() { // TODO: Add your command handler code here CircleDlg dlg; if(dlg.DoModal()==IDOK) { R=dlg.m_R;

} AfxGetMainWnd()->SetWindowText("中点算法"); RedrawWindow(); GetMaxX();GetMaxY(); MidPoint(); } void CCircleView::OnMENUEr() { } // TODO: Add your command handler code here CircleDlg dlg; if(dlg.DoModal()==IDOK) { R=dlg.m_R; } AfxGetMainWnd()->SetWindowText("二阶差分算法"); RedrawWindow(); GetMaxX();GetMaxY(); Erjie(); 实验环境 VC 6.0 MFC

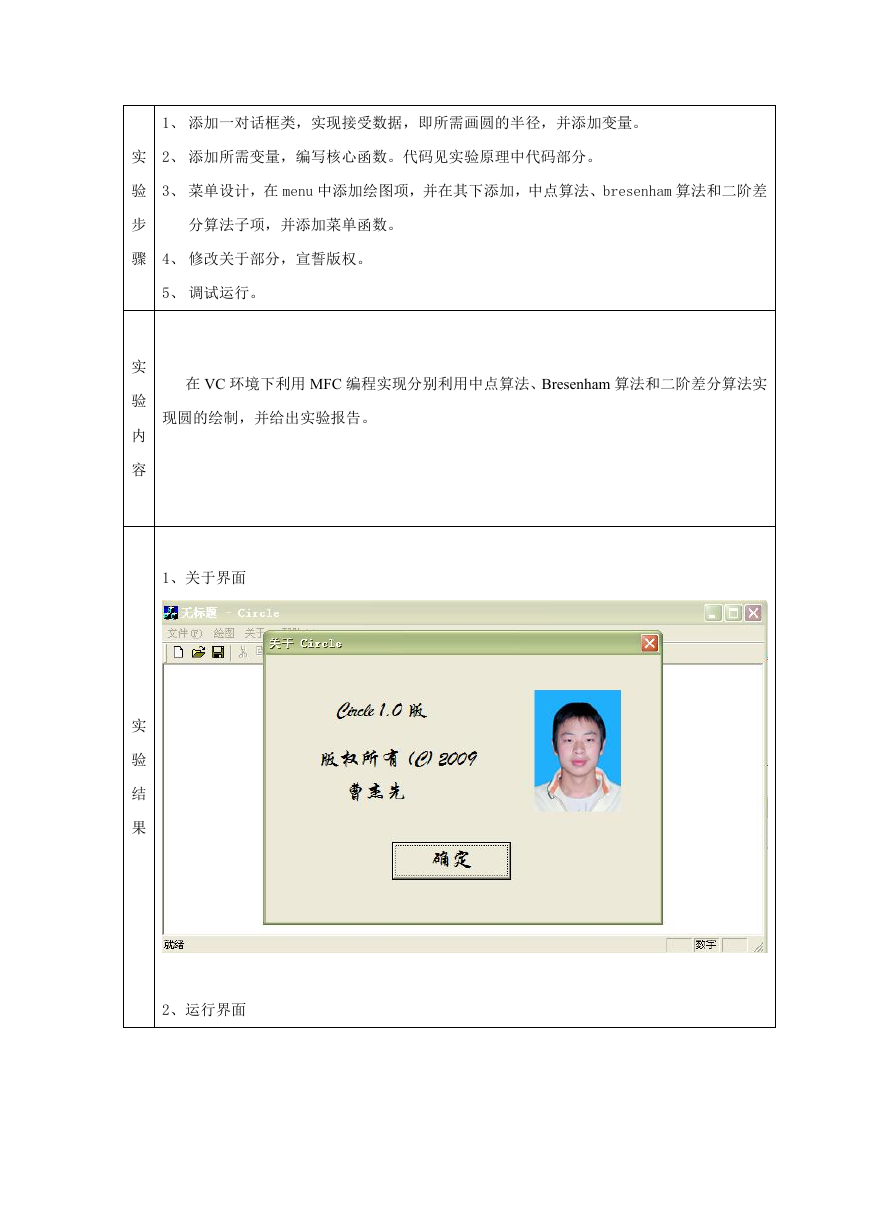
1、添加一对话框类，实现接受数据，即所需画圆的半径，并添加变量。实 2、添加所需变量，编写核心函数。代码见实验原理中代码部分。验 3、菜单设计，在 menu 中添加绘图项，并在其下添加，中点算法、bresenham 算法和二阶差步分算法子项，并添加菜单函数。骤 4、修改关于部分，宣誓版权。 5、调试运行。实验内容实验结果在 VC 环境下利用 MFC 编程实现分别利用中点算法、Bresenham 算法和二阶差分算法实现圆的绘制，并给出实验报告。 1、关于界面 2、运行界面

分享到：

赞收藏

资料库

vc实现圆的生成算法实验报告.doc

相关推荐

开发技术

热门标签

最新资料