图形处理器架构(GPU_Architecture)与图形管线(Graphics

xiucaijiang-2827573-4744300845384435578.pdf-第1页.png

第1页 / 共24页

xiucaijiang-2827573-4744300845384435578.pdf-第2页.png

第2页 / 共24页

xiucaijiang-2827573-4744300845384435578.pdf-第3页.png

第3页 / 共24页

xiucaijiang-2827573-4744300845384435578.pdf-第4页.png

第4页 / 共24页

xiucaijiang-2827573-4744300845384435578.pdf-第5页.png

第5页 / 共24页

xiucaijiang-2827573-4744300845384435578.pdf-第6页.png

第6页 / 共24页

xiucaijiang-2827573-4744300845384435578.pdf-第7页.png

第7页 / 共24页

xiucaijiang-2827573-4744300845384435578.pdf-第8页.png

第8页 / 共24页

GPUs - Graphics Processing Units Minh Tri Do Dinh Minh.Do-Dinh@student.uibk.ac.at Vertiefungsseminar Architektur von Prozessoren, SS 2008 Institute of Computer Science, University of Innsbruck July 7, 2008 This paper is meant to provide a closer look at modern Graphics Processing Units. It explores their architecture and underlying design principles, using chips from Nvidia’s ”Geforce” series as examples. 1 Introduction Before we dive into the architectural details of some example GPUs, we’ll have a look at some basic concepts of graphics processing and 3D graphics, which will make it easier for us to understand the functionality of GPUs 1.1 What is a GPU? A GPU (Graphics Processing Unit) is essentially a dedicated hardware device that is responsible for trans- lating data into a 2D image formed by pixels. In this paper, we will focus on the 3D graphics, since that is what modern GPUs are mainly designed for. 1.2 The anatomy of a 3D scene 3D scene: A collection of 3D objects and lights. Figure 1: A 3D scene 1

Figure 2: Object, triangle and vertices 3D objects: Arbitrary objects, whose geometry consists of triangular polygons. Polygons are composed of vertices. Vertex: A Point with spatial coordinates and other information such as color and texture coordinates. Figure 3: A cube with a checkerboard texture Texture: An image that is mapped onto the surface of a 3D object, which creates the illusion of an object consisting of a certain material. The vertices of an object store the so-called texture coordinates (2-dimensional vectors) that specify how a texture is mapped onto any given surface. Figure 4: Texture coordinates of a triangle with a brick texture 2

In order to translate such a 3D scene to a 2D image, the data has to go through several stages of a ”Graphics Pipeline” 1.3 The Graphics Pipeline Figure 5: The 3D Graphics Pipeline First, among some other operations, we have to translate the data that is provided by the application from 3D to 2D. 1.3.1 Geometry Stage This stage is also referred to as the ”Transform and Lighting” stage. In order to translate the scene from 3D to 2D, all the objects of a scene need to be transformed to various spaces - each with its own coordinate system - before the 3D image can be projected onto a 2D plane. These transformations are applied on a vertex-to-vertex basis. Mathematical Principles If we keep using 3-dimensional A point in 3D space usually has 3 coordinates, specifying its position. vectors for the transformation calculations, we run into the problem that diﬀerent transformations require diﬀerent operations (e.g.: translating a vertex requires addition with a vector while rotating a vertex requires multiplication with a 3x3 matrix). We circumvent this problem simply by extending the 3-dimensional vector by another coordinate (the w-coordinate), thus getting what is called homogeneous coordinates. This way, every transformation can be applied by multiplying the vector with a speciﬁc 4x4 matrix, making calculations much easier. Figure 6: Transformation matrices for translation, rotation and scaling 3

Lighting, the other major part of this pipeline stage is calculated using the normal vectors of the surfaces of an object. In combination with the position of the camera and the position of the light source, one can compute the lighting properties of a given vertex. Figure 7: Calculating lighting For transformation, we start out in the model space where each object (model) has its own coordinate system, which facilitates geometric transformations such as translation, rotation and scaling. After that, we move on to the world space, where all objects within the scene have a uniﬁed coordinate system. Figure 8: World space coordinates The next step is the transformation into view space, which locates a camera in the world space and then transforms the scene, such that the camera is at the origin of the view space, looking straight into the positive z-direction. Now we can deﬁne a view volume, the so-called view frustrum, which will be used to decide what actually is visible and needs to be rendered. 4

Figure 9: The camera/eye, the view frustrum and its clipping planes After that, the vertices are transformed into clip space and assembled into primitives (triangles or lines), which sets up the so-called clipping process. While objects that are outside of the frustrum don’t need to be rendered and can be discarded, objects that are partially inside the frustrum need to be clipped (hence the name), and new vertices with proper texture and color coordinates need to be created. A perspective divide is then performed, which transforms the frustrum into a cube with normalized coordinates (x and y between -1 and 1, z between 0 and 1) while the objects inside the frustrum are scaled accordingly. Having this normalized cube facilitates clipping operations and sets up the projection into 2D space (the cube simply needs to be ”ﬂattened”). Figure 10: Transforming into clip space Finally, we can move into screen space where x and y coordinates are transformed for proper 2D display (in a given window). (Note that the z-coordinate of a vertex is retained for later depth operations) Figure 11: From view space to screen space 5

Note, that the texture coordinates need to be transformed as well and additionally besides clipping, sur- faces that aren’t visible (e.g. the backside of a cube) are removed as well (so-called back face culling). The result is a 2D image of the 3D scene, and we can move on to the next stage. 1.3.2 Rasterization Stage Next in the pipeline is the Rasterization stage. The GPU needs to traverse the 2D image and convert the data into a number of ”pixel-candidates”, so-called fragments, which may later become pixels of the ﬁnal image. A fragment is a data structure that contains attributes such as position, color, depth, texture coordinates, etc. and is generated by checking which part of any given primitive intersects with which pixel of the screen. If a fragment intersects with a primitive, but not any of its vertices, the attributes of that fragment have to be additionally calculated by interpolating the attributes between the vertices. Figure 12: Rasterizing a triangle and interpolating its color values After that, further steps can be made to obtain the ﬁnal pixels. Colors are calculated by combining textures with other attributes such as color and lighting or by combining a fragment with either another translucent fragment (so-called alpha blending) or optional fog (another graphical eﬀect). Visibility checks are performed such as: • Scissor test (checking visibility against a rectangular mask) • Stencil test (similar to scissor test, only against arbitrary pixel masks in a buﬀer) • Depth test (comparing the z-coordinate of fragments, discarding those which are further away) • Alpha test (checking visibility against translucent fragments) Additional procedures like anti-aliasing can be applied before we achieve the ﬁnal result: a number of pixels that can be written into memory for later display. This concludes our short tour through the graphics pipeline, which hopefully gives us a better idea of what kind of functionality will be required of a GPU. 6

2 Evolution of the GPU Some historical key points in the development of the GPU: • Eﬀorts for real time graphics have been made as early as 1944 (MIT’s project ”Whirlwind”) • In the 1980s, hardware similar to modern GPUs began to show up in the research community (“Pixel- Planes”, a a parallel system for rasterizing and texture-mapping 3D geometry • Graphic chips in the early 1980s were very limited in their functionality • In the late 1980s and early 1990s, high-speed, general-purpose microprocessors became popular for implementing high-end GPUs (e.g. Texas Instruments’ TMS340) • 1985 The ﬁrst mass-market graphics accelerator was included in the Commodore Amiga • 1991 S3 introduced the ﬁrst single chip 2D-accelerator, the S3 86C911 • 1995 Nvidia releases one of the ﬁrst 3D accelerators, the NV1 • 1999 Nvidia’s Geforce 256 is the ﬁrst GPU to implement Transform and Lighting in Hardware • 2001 Nvidia implements the ﬁrst programmable shader units with the Geforce 3 • 2005 ATI develops the ﬁrst GPU with uniﬁed shader architecture with the ATI Xenos for the XBox 360 • 2006 Nvidia launches the ﬁrst uniﬁed shader GPU for the PC with the Geforce 8800 7

3 From Theory to Practice - the Geforce 6800 3.1 Overview Modern GPUs closely follow the layout of the graphics pipeline described in the ﬁrst section. Using Nvidia’s Geforce6800 as an example we will have a closer look at the architecture of modern day GPUs. Since being founded in 1993, the company NVIDIA has become one of the biggest manufacturers of GPUs (besides ATI), having released important chips such as the Geforce 256, and the Geforce 3. Launched in 2004, the Geforce 6800 belongs to the Geforce 6 series, Nvidia’s sixth generation of graphics chipsets and the fourth generation that featured programmability (more on that later). 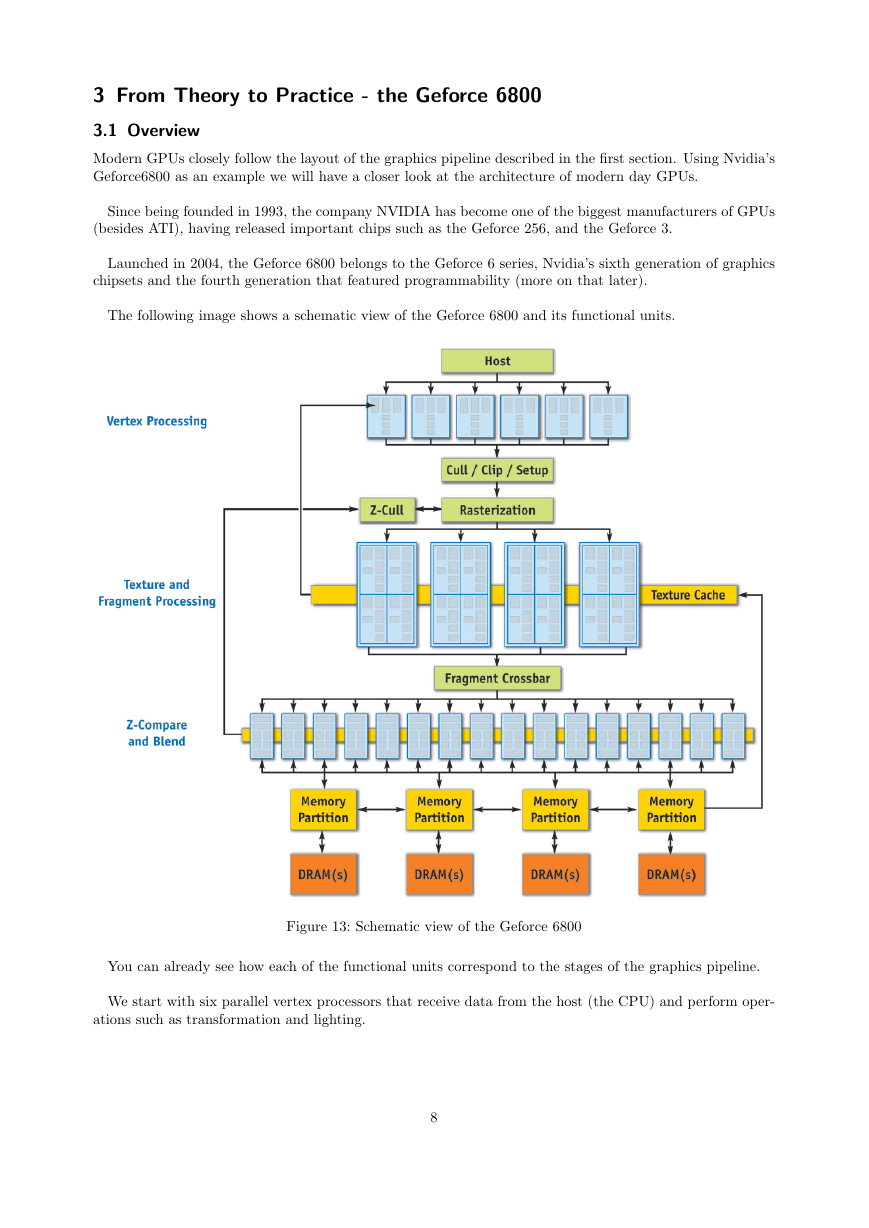The following image shows a schematic view of the Geforce 6800 and its functional units. Figure 13: Schematic view of the Geforce 6800 You can already see how each of the functional units correspond to the stages of the graphics pipeline. We start with six parallel vertex processors that receive data from the host (the CPU) and perform oper- ations such as transformation and lighting. 8

资料库

图形处理器架构(GPU_Architecture)与图形管线(Graphics_Pipeline)入门.pdf

相关推荐

开发技术

热门标签

最新资料