基于神经网络的多电机同步控制 基于神经网络的多电机同步控制 在造纸、印染、纺织等高精度、高转速传动系统中，随着工业自动化程度的提高和生产规模的扩大，采用单电 机驱动往往难以满足生产的要求。而多电机同步控制历来是最核心的问题，对多电机同步协调控制，国内、外 同行也有不少研究。在实际应用中，多电机的同步性能会因各传动轴的驱动特性不匹配、负载的扰动等因素的 影响而恶化，因此同步控制方法的好坏直接影响着系统的可靠性。 1 引言 在造纸、印染、纺织等高精度、高转速传动系统中，随着工业自动化程度的提高和生产规模的扩大，采用单电机驱动往往 难以满足生产的要求。而 本文通过对的多电机同步传动系统主要控制策略分析，得出改进的耦合控制是当前比较好的控制思想，实际应用中采用易 于实现的PID作为同步补偿控制器算法。但传统PID控制器结构简单、鲁棒性较差且抗扰动能力也不太理想。因此在控制策略 上，采用神经网络控制和PID控制算法相结合的方法。仿真结果表明，将该方法用于多电机同步控制中，不仅具有良好的动态 性能，而且整个系统同步精度也有所提高。 2 多电机同步控制的原理 对于多电机同步 3 基于神经网络PID控制器的建立 BP神经网络是应用最广泛的一种人工神经网络，在各门学科领域中都具有很重要的实用价值，根据本系统的控制系统的特 点，为了快速消除同步误差，本文采用BP神经网络与PID相结合的作为同步补偿方法。 3．1 BP神经网络PID控制系统的结构 基于BP网络的PID控制系统结构如图2所示，控制器由两部分组成： (1)常规PID控制器，直接对被控对象进行闭环控制，并且其控制参数Kp、Ki、Kd为在线调整方式； (2)BP神经网络，根据系统的运行状态，调节PID控制器的参数，以期达到某种性能指标的最优化，使输出层神经元的输出对 应于PID控制器的3个可调参数KD、Ki、Kd。通过BP神经网络的自学习、加权系数的调整，使BP神经网络输出对应于某种最 优控制规律下的PID控制器参数。以电机作为控制对像，一般采用增量式PID控制算法进行控制。它的控制算式为： 式中KP、KI、KD分别为比例、积分、微分系数． 3．2 神经网络PID的算法实现 

1)训练阶段的工作 第l步：设计输入输出神经元。本BP网络的输入层设置3个神经元，分别为输入速度vi、速度偏差e和偏差变化量△e，输出层 有3个神经元，为PID控制器的3个可调节参数Kp、Ki、Kd 第2步：设计隐含层神经元个数。本文初步确定隐含层节点数为5个．学习一定次数后，不成功再增加隐含层节点数，一直 达到比较合理的神经元数为止； 第3步：设计网络初始值。本文中设定的学习次数N=5000次，误差限定值E=0．02； 第4步：应用Simulink对BP网络进行训练和仿真。 2) 在测试阶段，主要是对训练过的网络输入测试样木，测试网络的学习效果，即判断网络的运算值与样本的期望值之差是否 在允许的范围之内。在此不再赘述具体判定过程。 4 仿真与分析 本文以2台电机同步为模型进行仿真。在电机的参数设定时，对2台电机的参数取相同值。电机参数为：定子每相绕组电阻 R=5．9Ω，定子d相绕组电感Ld=0．573，转子电阻R=5．6Ω转子电感L=O．58给定转速n=500rad／sec，极对数为3。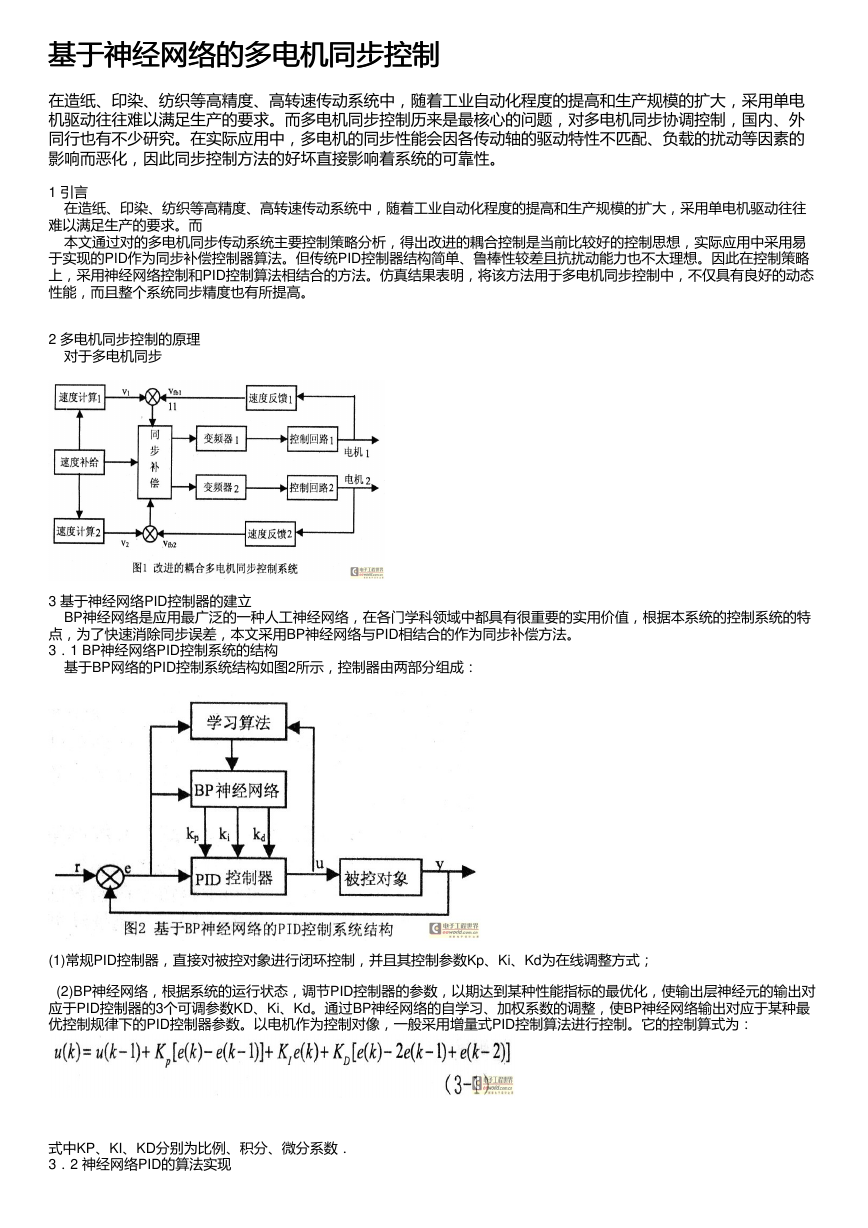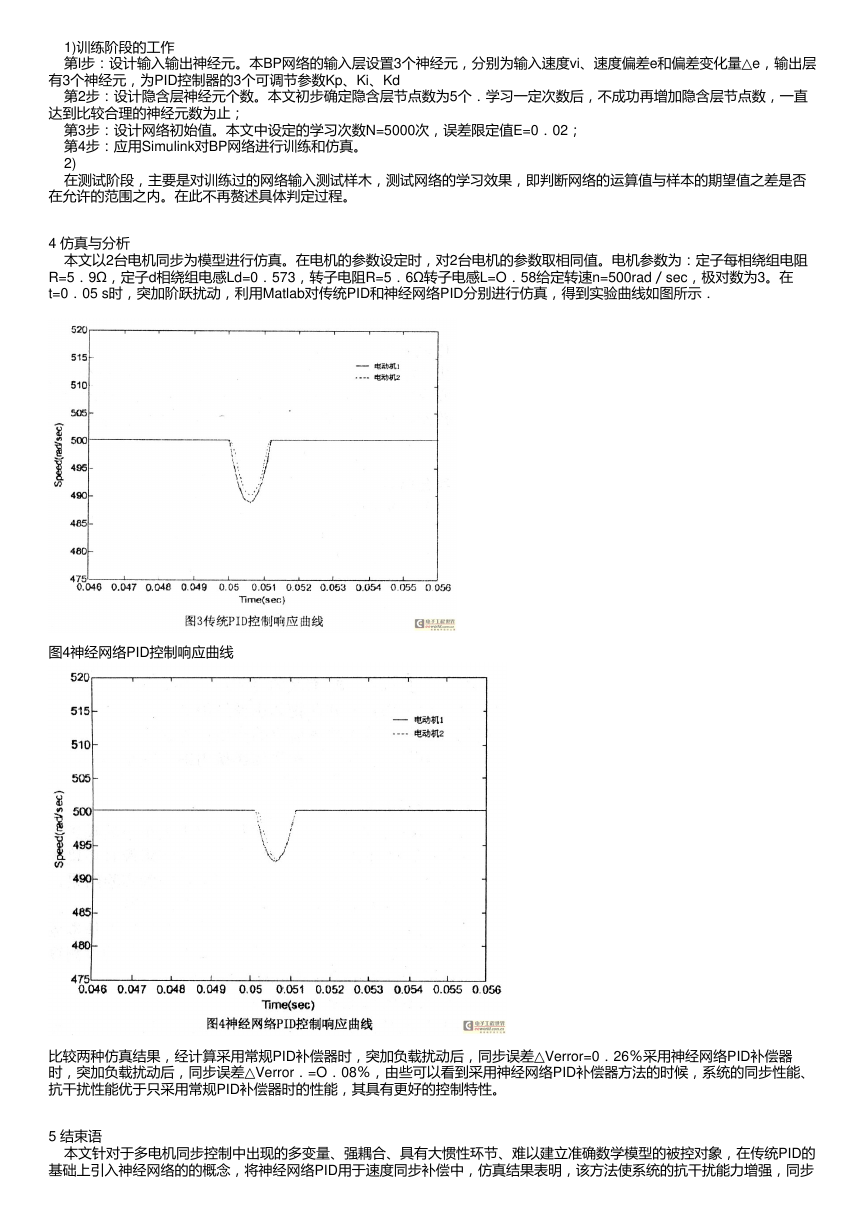在 t=0．05 s时，突加阶跃扰动，利用Matlab对传统PID和神经网络PID分别进行仿真，得到实验曲线如图所示． 图4神经网络PID控制响应曲线 比较两种仿真结果，经计算采用常规PID补偿器时，突加负载扰动后，同步误差△Verror=0．26％采用神经网络PID补偿器 时，突加负载扰动后，同步误差△Verror．=O．08％，由些可以看到采用神经网络PID补偿器方法的时候，系统的同步性能、 抗干扰性能优于只采用常规PID补偿器时的性能，其具有更好的控制特性。 5 结束语 本文针对于多电机同步控制中出现的多变量、强耦合、具有大惯性环节、难以建立准确数学模型的被控对象，在传统PID的 基础上引入神经网络的的概念，将神经网络PID用于速度同步补偿中，仿真结果表明，该方法使系统的抗干扰能力增强，同步 

精度有所提高，控制效果良好。