logo资料库

基于共轭梯度法的全波形反演.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.99M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    第45卷 第1期 煤田地质与勘探 Vol. 45 No.1 2017年2月 COAL GEOLOGY & EXPLORATION Feb. 2017 收稿日期: 2015-12-15 基金项目: 国家重点研发计划课题(2016YFC0501102)；国家自然基金煤炭联合基金项目(U1261203)；山西省煤层气联合研究基金资助项目(2013012001) Foundation item：National Key Research and Development Program(2016YFC0501102); Coal United Project of National Natural Science Foundation(U1261203); Shanxi Provincial Basic Research Program—Coalbed Methane Joint Research Foundation(2013012001) 第一作者简介: 林朋(1990—)，男，安徽阜阳人，硕士研究生，从事地球物理正演和反演研究. E-mail：linpeng798@126.com 引用格式: 林朋，彭苏萍，卢勇旭，等. 基于共轭梯度法的全波形反演[J]. 煤田地质与勘探，2017，45(1)：131–136. LIN Peng，PENG Suping，LU Yongxu，et al. Full waveform inversion based on the conjugate gradient method[J]. Coal Geology & Exploration，2017，45(1)：131–136. 文章编号: 1001-1986(2017)01-0131-06 基于共轭梯度法的全波形反演 林 朋，彭苏萍，卢勇旭，汪滔滔 (中国矿业大学(北京)煤炭资源与安全开采国家重点实验室，北京 100083) 摘要: 全波形反演是一种全新的地震成像方法，主要利用全波形信息反演地下介质参数，通过非线性优化波场理论值和观测值的残差实现波形反演。基于时间域声波方程，建立了时间域波场残差目标函数，以分层模型为例，分别从波场精度、目标函数收敛性和运行时间3个方面，比较了共轭梯度(Conjugate Gradient，CG)算法和拟牛顿算法(Broyden-Fletcher- Goldfarb-Shanno，BFGS)反演的效果。同时，应用共轭梯度法对正、逆断层模型和Marmousi模型进行了速度结构反演。反演结果表明：共轭梯度法计算效率较高，反演得到的速度模型精度更高，反演效果较好，是一种有效的波形反演方法。 关 键 词：全波形反演；共轭梯度法；BFGS；声波方程 中图分类号：P631 文献标识码：A DOI: 10.3969/j.issn.1001-1986.2017.01.026 Full waveform inversion based on the conjugate gradient method LIN Peng, PENG Suping, LU Yongxu, WANG Taotao (State Key Laboratory of Coal Resources and Safe Mining, China University of Mining and Technology(Beijing), Beijing 100083, China) Abstract: Full waveform inversion is a new seismic imaging method, which mainly uses full waveform informa-tion to inverse parameters of medium in the subsurface, and realizes waveform inversion by minimizing the resid-ual between observed wavefield and theoretical wavefield using nonlinear optimization methods. The objective function of wavefield residual was established based on time domain acoustic wave equation. To test the capability of conjugate gradient(CG) algorithm and BFGS Quasi-Newton algorithm, waveform inversion was applied to a hi-erarchical model. The inversion effect was compared from wavefield precision, objective function convergence and running time respectively. The CG method was used to reconstruct velocity model on positive, reverse fault and Marmousi models. The inversion results show that the CG method has higher computation efficiency and inversion precision. The CG method is a promising method for full waveform inversion. Keywords: full waveform inversion; conjugate gradient algorithm; BFGS; acoustic wave equation 全波形反演(Full Waveform Inversion，FWI)是一种利用整个或部分波形信息进行地下介质参数反演的方法，由于利用的波形信息比较全面，因而具有较高分辨率和刻画精度，对地质勘探具有指导性意义，成为当前研究的热点。全波形反演最早由P Lailly[1]与A Tarantola[2-3]提出，利用波场残差作为目标函数，提出了梯度计算新方法，基于最速下降法在时间域实现了波形反演，对其后全波形反演理论体系的建立和发展具有重大影响；R G Pratt等[4-6]在频率域实现了全波形参数反演，即层析成像，通过虚震源计算波场实现波形反演，奠定了频率域全波形反演的基础，使全波形反演理论进一步实用化；C Shin等[7-9]建立了拉普拉斯域全波形反演，有效的解决了频率域和时间域面临局部收敛的问题，开辟了全波形反演的另一途径，但是由于只利用了相位、零频信息，导致其反演分辨率相对较低；P Mora[10-11]中国煤炭期刊网 www.chinacaj.net
    · 132 · 煤田地质与勘探 第45卷 通过共轭梯度法实现了二维地震资料的全波形反演，证明了全波形反演建模的高精度，但其对初始模型具有较大的依赖性；C Ravaut等[12]通过对角海森矩阵尺度化方法实现了频率域FWI二维时间域声波方程的速度反演；L Sirgue[13]应用三维全波形反演技术于挪威北海油田，复杂构造地区得到了详细刻画，使得全波形反演的实际应用进一步提升；L Metivier等[14-15]提出了基于截断牛顿法的全波形反演，利用二阶伴随状态算子计算海森矩阵，虽计算效率不高，但反演结果比传统的2D声波频率域全波形反演方法较好；刘璐等[16]将改进的Broyden- Fletcher-Goldfarb-Shanno(BFGS)算法应用于2D频率域声波方程的速度反演中，对于BFGS算法进行了一定程度的优化，提高了反演效率；王义等[17]基于截断牛顿法对Hessian逆算子进行了估计，在时间域研究了VTI介质的双参数同时反演；刘玉柱等[18]在Born敏感核函数基础上，进行了VTI介质的多参数波形反演，有效解决了Hessian矩阵储存较大的难题。 本次主要从共轭梯度法(Conjugate Gradient，CG)出发，利用传统的伴随状态法求取梯度，使用共轭梯度法实现对目标函数的最优化，通过分层模型的二维时间域声波方程波形反演，对比了CG法和BFGS算法反演的优劣性。为进一步研究CG法的反演有效性，分别使用了断层模型和Marmousi模型进行了速度反演。 1 方法原理 1.1 目标函数 全波形反演主要是利用波场的实际值和观测值，求取波场数据残差，所对应的目标函数为 Tobsobs1=2Ebbmmfmf (1) 式中 E表示优化目标函数，m为地球物理模型参数，b(m)表示波场理论值，fobs为波场观测值，b表述了依赖于模型参数的地震波场正传播过程，表达了地震波场传播的正算子[19]。本次研究基于声波方程，采用有限差分法求解时间二阶、空间四阶的常密度声波方程。令p表示声压，v表示速度，二维时间域常密度声波方程可表示如式(2) [20]。 22222221ppptxz (2) 1.2 梯度计算 梯度计算是全波形反演的关键部分，代表着模型的更新方向。梯度导引类反演方法通过目标泛函对模型参数的导数，来寻找迭代更新方向，以实现对模型的更新。由于全波形反演问题是高度非线性、病态的优化问题，为了求解目标函数对参数的梯度，提高计算效率，R E Plessix[21]提出了基于伴随状态法的梯度求取方法。即将正传波场和反传波场的数据残差作为新的震源进行正演，以求取目标函数对模型的梯度[19]。 模型更新公式为 1kkkkmmd (3) 式中 k是通过线性搜索确定的第k步的步长，dk是第k步模型的更新方向。 由目标函数可知，所求解问题为无约束优化最小值问题，主要有梯度类和牛顿类两类方法。共轭梯度法是求解非线性无约束优化问题的常用梯度类方法，在计算时仅需要一阶导数信息，克服了最速下降法收敛慢的缺点，同时避免了牛顿法需要存储和计算Hessian矩阵求逆的缺点。共轭梯度法是在梯度的方向上，在下一次迭代时，利用两次的梯度方向信息，构造一个共轭梯度方向作为新的搜索方向，通过线性搜索确定最佳步长，从而实现了快速迭代求取最优解[22]。 令E(m)表示目标函数对模型mk的梯度，共轭梯度法中模型更新方向为 01, 0, 1kkkkEkEk≥mdmd (4) 为了保证全局收敛性，k的更新采用HS法[23]和Dai-Yuan法[24]的混合共轭梯度法： HSDY=max0,min,kkk (5) 1HS11DY11,,, ,kkkkkkkkkkkkkEEEEEEEEEmmmdmmmmdmm (6) 拟牛顿算法是牛顿类方法的代表，主要是利用目标函数的一阶导数和二阶导数共同构造模型的更新方向。但在计算中Hessian矩阵具有高度的复杂性，其保存和计算难度较大，限制了其大规模应用[22]。BFGS算法是牛顿类方法的代表，是在满足拟牛顿方程的基础上，由Broyden-Fletcher-Goldfard- Shanno 4人提出的二阶导数计算方法，用于近似计算Hessian矩阵。拟牛顿算法中更新方向满足以下方程 1kkkEdHmm (7) 式中 Hessian矩阵H为目标函数对模型参数mk的二阶导数。BFGS算法给出的二阶导数计算公式如式(8)所示[22]。 中国煤炭期刊网 www.chinacaj.net
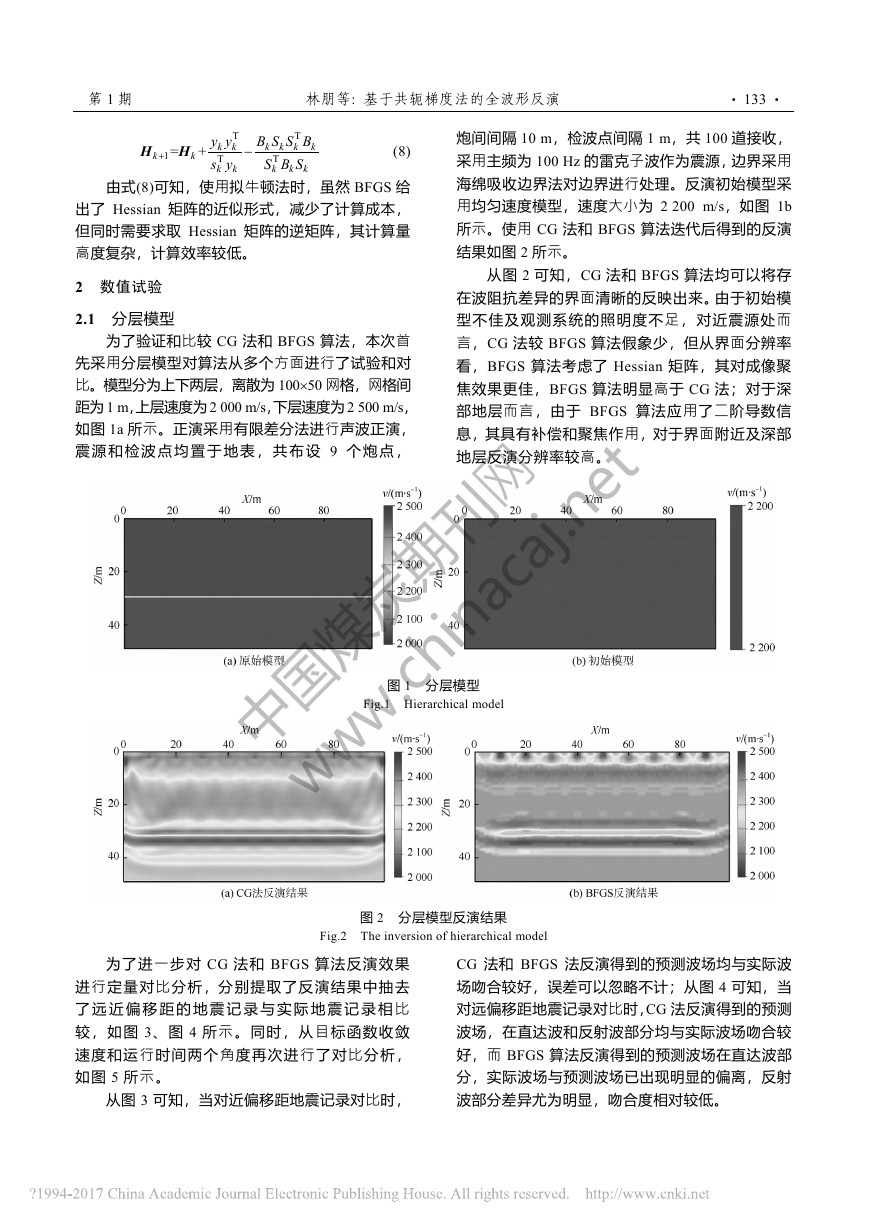
    第1期 林朋等: 基于共轭梯度法的全波形反演 · 133 · TT1TT=+kkkkkkkkkkkkkyyBSSBsySBSHH (8) 由式(8)可知，使用拟牛顿法时，虽然BFGS给出了Hessian矩阵的近似形式，减少了计算成本，但同时需要求取Hessian矩阵的逆矩阵，其计算量高度复杂，计算效率较低。 2 数值试验 2.1 分层模型 为了验证和比较CG法和BFGS算法，本次首先采用分层模型对算法从多个方面进行了试验和对比。模型分为上下两层，离散为10050网格，网格间距为1 m，上层速度为2 000 m/s，下层速度为2 500 m/s，如图1a所示。正演采用有限差分法进行声波正演，震源和检波点均置于地表，共布设9个炮点， 炮间间隔10 m，检波点间隔1 m，共100道接收，采用主频为100 Hz的雷克子波作为震源，边界采用海绵吸收边界法对边界进行处理。反演初始模型采用均匀速度模型，速度大小为2 200 m/s，如图1b所示。使用CG法和BFGS算法迭代后得到的反演结果如图2所示。 从图2可知，CG法和BFGS算法均可以将存在波阻抗差异的界面清晰的反映出来。由于初始模型不佳及观测系统的照明度不足，对近震源处而言，CG法较BFGS算法假象少，但从界面分辨率看，BFGS算法考虑了Hessian矩阵，其对成像聚焦效果更佳，BFGS算法明显高于CG法；对于深部地层而言，由于BFGS算法应用了二阶导数信息，其具有补偿和聚焦作用，对于界面附近及深部地层反演分辨率较高。 图1 分层模型 Fig.1 Hierarchical model 图2 分层模型反演结果 Fig.2 The inversion of hierarchical model为了进一步对CG法和BFGS算法反演效果进行定量对比分析，分别提取了反演结果中抽去了远近偏移距的地震记录与实际地震记录相比较，如图3、图4所示。同时，从目标函数收敛速度和运行时间两个角度再次进行了对比分析，如图5所示。 从图3可知，当对近偏移距地震记录对比时，CG法和BFGS法反演得到的预测波场均与实际波场吻合较好，误差可以忽略不计；从图4可知，当对远偏移距地震记录对比时，CG法反演得到的预测波场，在直达波和反射波部分均与实际波场吻合较好，而BFGS算法反演得到的预测波场在直达波部分，实际波场与预测波场已出现明显的偏离，反射波部分差异尤为明显，吻合度相对较低。 中国煤炭期刊网 www.chinacaj.net
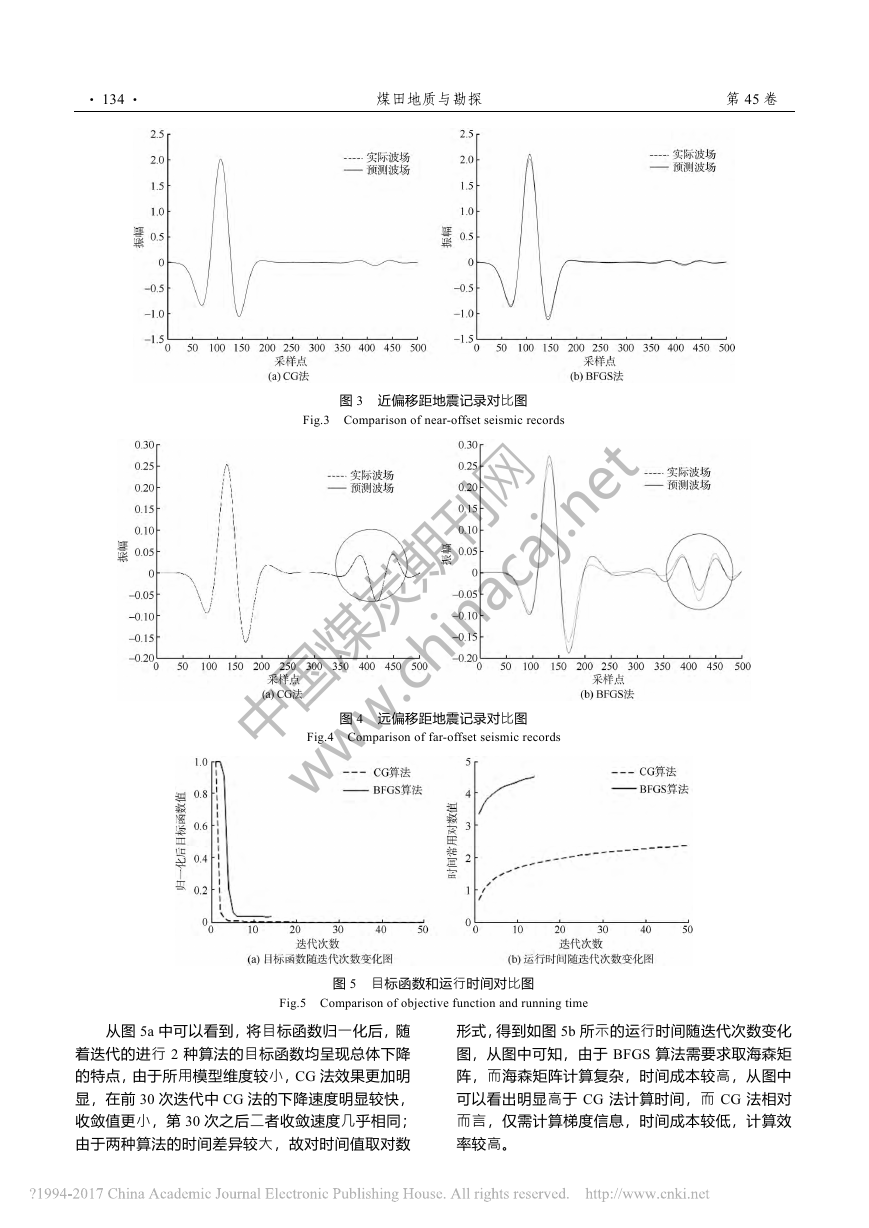
    · 134 · 煤田地质与勘探 第45卷 图3 近偏移距地震记录对比图 Fig.3 Comparison of near-offset seismic records 图4 远偏移距地震记录对比图 Fig.4 Comparison of far-offset seismic records 图5 目标函数和运行时间对比图 Fig.5 Comparison of objective function and running time 从图5a中可以看到，将目标函数归一化后，随着迭代的进行2种算法的目标函数均呈现总体下降的特点，由于所用模型维度较小，CG法效果更加明显，在前30次迭代中CG法的下降速度明显较快，收敛值更小，第30次之后二者收敛速度几乎相同；由于两种算法的时间差异较大，故对时间值取对数形式，得到如图5b所示的运行时间随迭代次数变化图，从图中可知，由于BFGS算法需要求取海森矩阵，而海森矩阵计算复杂，时间成本较高，从图中可以看出明显高于CG法计算时间，而CG法相对而言，仅需计算梯度信息，时间成本较低，计算效率较高。 中国煤炭期刊网 www.chinacaj.net
    第1期 林朋等: 基于共轭梯度法的全波形反演 · 135 · 2.2 断层模型 为观察CG法对于复杂模型的反演效果，原始模型分别采用正断层和逆断层模型进行反演。初始模型均采用图1b所示的均匀模型，正断层相关模型如图6所示，逆断层相关模型如图7所示。 从图6可知，使用CG法对正断层模型进行反 演时，CG法FWI可以将存在波阻抗差异的上盘和下盘详细刻画，断层的断点和断面清晰可见，对于构造的反演效果较好。从图7可以观察到，使用CG法对逆断层模型进行反演时，由于逆断层模型断点和断面的特殊性，反演效果不如正断层模型，但断层和断面的基本形状和位置已经十分明显，反演结果比较理想。 图6 正断层模型 Fig.6 Model of positive fault 图7 逆断层模型 Fig.7 Model of reverse fault 2.3 Marmousi模型 为了验证CG法反演的有效性，以Marmousi模型作为理论模型进行共轭梯度法反演，如图8所示。模型离散为383125网格，网格间距12 m，震源采用主频为10 Hz的雷克子波，采样间隔1.5 ms， 图8 Marmousi模型 Fig.8 Model of Marmousi 在地表处共布设12个炮点，炮间间隔360 m，布设检波点383道，检波点间隔12 m。平滑后的模型作为初始模型，如图9a所示，反演结果如图9b所示。 从图9中可知，CG法对于Marmousi模型的反演效果较好，误差较小。浅层的复杂断层得到了精细刻画，断点和断面清晰可见，反演精度较高；深层处两侧的高速异常体具有了明显的轮廓；初始模型中，深层的两处背斜均已消失，反演后的速度模型中，背斜构造十分清晰，层位较为明显。 为了更直观的展示CG法对速度细节的刻画，抽取了水平方向网格点150处(1 800 m)和250处(3 000 m)处2道速度曲线，对真实模型和反演结果进行对比，如图10所示。 从图10可知，由于浅层能量较强，CG法对于Marmousi模型的浅部反演较好，速度更新较准确，反演结果与实际速度拟合较好；对于深部而言，能量较少且分布不均，致反演精度逐渐降低，误差增大，但速度的变化趋势相同，偏差较小。 中国煤炭期刊网 www.chinacaj.net
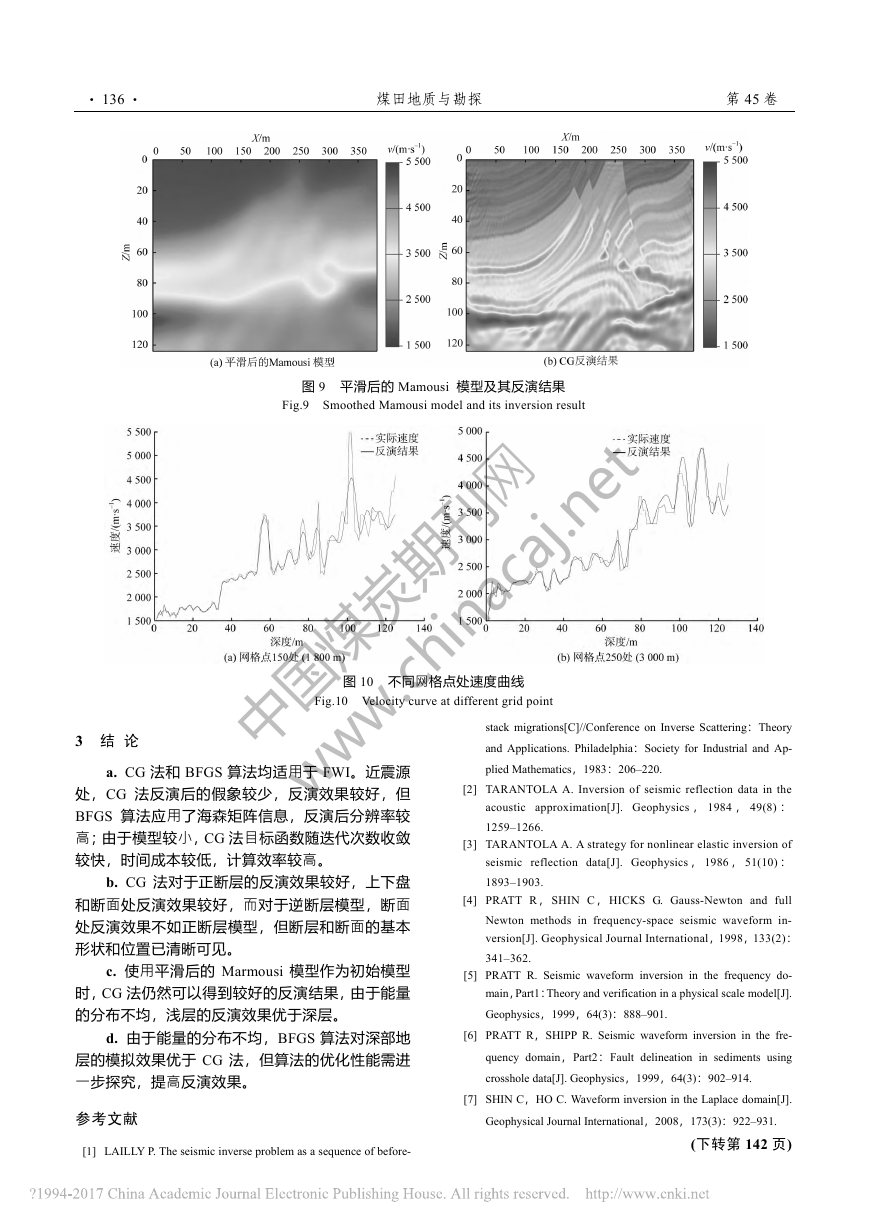
    · 136 · 煤田地质与勘探 第45卷 图9 平滑后的Mamousi 模型及其反演结果 Fig.9 Smoothed Mamousi model and its inversion result 图10 不同网格点处速度曲线 Fig.10 Velocity curve at different grid point 3 结 论 a. CG法和BFGS算法均适用于FWI。近震源处，CG法反演后的假象较少，反演效果较好，但BFGS算法应用了海森矩阵信息，反演后分辨率较高；由于模型较小，CG法目标函数随迭代次数收敛较快，时间成本较低，计算效率较高。 b. CG法对于正断层的反演效果较好，上下盘和断面处反演效果较好，而对于逆断层模型，断面处反演效果不如正断层模型，但断层和断面的基本形状和位置已清晰可见。 c. 使用平滑后的Marmousi模型作为初始模型时，CG法仍然可以得到较好的反演结果，由于能量的分布不均，浅层的反演效果优于深层。 d. 由于能量的分布不均，BFGS算法对深部地层的模拟效果优于CG法，但算法的优化性能需进一步探究，提高反演效果。 参考文献 [1] LAILLY P. The seismic inverse problem as a sequence of before- stack migrations[C]//Conference on Inverse Scattering：Theory and Applications. Philadelphia：Society for Industrial and Ap-plied Mathematics，1983：206–220. [2] TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics，1984，49(8)：1259–1266. [3] TARANTOLA A. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics，1986，51(10)：1893–1903. [4] PRATT R，SHIN C，HICKS G. Gauss-Newton and full Newton methods in frequency-space seismic waveform in-version[J]. Geophysical Journal International，1998，133(2)：341–362. [5] PRATT R. Seismic waveform inversion in the frequency do-main，Part1：Theory and verification in a physical scale model[J]. Geophysics，1999，64(3)：888–901. [6] PRATT R，SHIPP R. Seismic waveform inversion in the fre-quency domain，Part2：Fault delineation in sediments using crosshole data[J]. Geophysics，1999，64(3)：902–914. [7] SHIN C，HO C. Waveform inversion in the Laplace domain[J]. Geophysical Journal International，2008，173(3)：922–931. (下转第142页) 中国煤炭期刊网 www.chinacaj.net
    · 142 · 煤田地质与勘探 第45卷 XUE Dinghua. Analysis of the practical application of "radio wave perspective CT detection technology" in the well[J]. Coal, 2015，24(4)：60–62. [5] 高一峰. 无线电波透视在煤矿中的应用[J]. 物探与化探，2007，31(增刊1)：105–108. GAO Yifeng. The application of radio-wave transmission in coal mines[J]. Geophysical & Geochemical Exploration，2007，31(S1)：105–108. [6] 吴荣新，刘盛东，肖玉林，等. 工作面无线电波透视实测场强成像分析及应用[J]. 岩土力学，2010，31(增刊1)：435–440. WU Rongxin，LIU Shengdong，XIAO Yulin，et al. Imaging analysis of measured magnetic field intensity from radio wave penetration for coal face and its application[J]. Rock and Soil Mechanics，2010，31(S1)：435–440. [7] 程久龙，于师建，邱伟，等. 工作面电磁波高精度层析成像及其应用[J]. 煤田地质与勘探，1999，27(4)：62–64. CHENG Jiulong，YU Shijian，QIU Wei，et al. High accuracy computer tomography of electromagnetic wave on working faces amd its application[J]. Coal Geology & Exploration，1999，27(4)：62–64. [8] 程久龙，李文，王玉和. 工作面内隐伏含水体电法探测的实验研究[J]. 煤炭学报，2008，33(1)：59–62. CHENG Jiulong，LI Wen，WANG Yuhe. Simulation experiment on detecting the hidden water-bearing bodies in working face[J]. Journal of China Coal Society，2008，33(1)：59–62. [9] 程刚，张平松．矿井工作面地质异常精细探查方法技术研究进展[J]．工程地球物理学报，2013，10(1)：99–106. CHENG Gang，ZHANG Pingsong. Research progress of fine exploration method of geological abnomal in mine morking face[J]. Chinese Journal of Engineering Geophysics，2013，10(1)：99–106. [10] 内蒙古煤矿设计研究院有限责任公司. 鄂尔多斯市兴华能源有限责任公司唐家会矿井及选煤厂可行性研究报告[R]. 2010. [11] 田王健．基于无线电磁波透视工作面煤层情况探测[J]. 能源与节能，2014(6)：47–48. TIAN WangJian. Detection of coal seam in working face based on wireless electromagnetic wave[J]. Energy and Saving，2014(6)：47–48. (责任编辑 聂爱兰) (上接第136页) [8] SHIN C，HO C. Waveform inversion in the Laplace-Fourier domain[J]. Geophysical Journal International，2009，177(3)：1067–1079. [9] SHIN C. Laplace-domain full-waveform inversion of seismic data lacking low-frequency information[J]. Geophysics，2012，77(5)：199–206. [10] MORA P. Nonlinear two-dimensional elastic inversion of mul-tioffset seismic data[J]. Geophysics，1987，52(9)：1211–1228. [11] MORA P. Elastic wave-field inversion of reflection and trans-mission data[J]. Geophysics，1988，53(6)：750–759. [12] RAVAUT C，OPERTO S，IMPORTA L，et al. Multiscale imaging of complex structures from multifold wide-aperture seismic data by frequency-domain full-waveform tomography：Application to a thrust belt[J]. Geophysical Journal International，2004，159(3)：1032–1056. [13] SIRGUE L，PRAAT R. Efficient waveform inversion and im-aging：A strategy for selecting temporal frequencies[J]. Geo-physics，2004，69(1)：231–248. [14] METIVIER L，BROSSOER R，VIRIEUX J，et al. Full waveform inversion and the truncated Newton method[J]. Society for In-dustrial and Applied Mathematics Journal on Scientific Comput-ing，2013，35(2)：401–437. [15] MéTIVIER L，BRETAUDEAU F，BROSSIER R，et al. Full waveform inversion and the truncated Newton method：Quantitative imaging of complex subsurface structures[J]. Geo-physical Prospecting，2014，62(6)：1353–1375. [16] 刘璐，刘洪，张衡，等. 基于修正拟牛顿公式的全波形反演[J]. 地球物理学报，2013，56(7)：2447–2451. LIU Lu，LIU Hong，ZHANG Heng，et al. Full waveform in-version based on modified quasi-Newton equation[J]. Chinese Journal Geophysics(in Chinese)，2013，56(7)：2447–2451. [17] 王义，董良国. 基于截断牛顿法的VTI介质声波多参数全波形反演[J]. 地球物理学报，2015，58(8)：2873–2885. WANG Yi，DONG Liangguo. Multi-Parameter full waveform inversion for acoustic VTI media using the truncated Newton method[J]. Chinese Journal Geophysics(in Chinese)，2015，58(8)：2873–2885. [18] 刘玉柱，王光银，杨积忠，等. 基于Born敏感核函数的VTI介质多参数全波形反演[J]. 地球物理学报，2015，58(4)：1305–1316. LIU Yuzhu，WANG Guangyin，YANG Jizhong，et al. Multi-parameter full waveform inversion for VTI media based on Born sensitivity kernels[J]. Chinese Journal Geophysics(in Chi-nese)，2015，58(4)：1305–1316. [19] 胡光辉，王立歆，方伍宝，等. 全波形反演及应用[M]. 北京：石油工业出版社，2014. [20] 陈洪杰. 基于声波方程的数值模拟与逆时偏移方法研究[D]. 长春：吉林大学，2010. [21] PLESSIX R E. A review of the adjoint-state method for comput-ing the gradient of a functional with geophysical applications[J]. Geophysical Journal International，2006，167(2)：495–503. [22] 高凤霞. 频率域波动方程多参数全波形反演方法研究[D]. 长春：吉林大学，2014. [23] HESTENES M R E, STIEFEL E. Methods of conjugate gradients for solving linear systems[J]. Journal of Research of the National Bureau of Standards, 1952，49(6)：409–436. [24] DAI Y，YUAN Y. A nonlinear conjugate gradient method with a strong global convergence property[J]. Society for Industrial and Applied Mathematics Journal on Optimization，1999，10(1)：177–182. (责任编辑 聂爱兰) 中国煤炭期刊网 www.chinacaj.net
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料