logo资料库

数控直线运动工作台位置控制系统matlab仿真.docx

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.50M 资料格式：docx 举报 版权申诉
第1页 / 共13页
第2页 / 共13页
第3页 / 共13页
第4页 / 共13页
第5页 / 共13页
第6页 / 共13页
第7页 / 共13页
第8页 / 共13页
资料共13页，剩余部分请下载后查看
    数控直线运动工作台位置控制系统 一、建立数控运动工作台的数学模型 如下图是一个简化了的数控直线运动工作台位置控制系统示意 图。其中，伺服电动机为电枢控制式直一流电动机，工作台采用滚珠 丝杠传动，而工作台移动采用直线滚动导轨。电动机转子轴上的转动 惯量为 1J ，减速器输出轴上的转动惯量为 2J ，减速器的减速比为i， 滚珠丝杠的螺距为P，工作台的质量为m。给定环节的传递函数为 aK 。， 放大环节的传递函数为 bK ，包括检测装置在内的反馈环节的传递函数 为 cK 。考虑到采用了滚动轴承、滚珠丝杠和直线滚动导轨，与各运动 副相对速度有关的黏性阻尼力矩可忽略不计，同时，由于运动部件的 弹性变形非常小，也忽略与运动部件弹性形变相关的弹性力矩 根据动量守恒定理，折算前后系统的总能量保持不变，则有 即 1 2 2 J   J 1 2  J 2  1 J 1   1 2 m(   2 i  2 ) 2 )  2 J 1 2 J 2 m(  2 i 1 (  i  2 i  2 ) 令负载力矩 (s) 0  ,可以得到系统在给定输入 ( ) iX s 作用下的传递函 LM 数为： ( ) G s X i  3 JLs  JRs k K K K 1 b m a 2 k k s   d m k K K K m 1 b （1） c
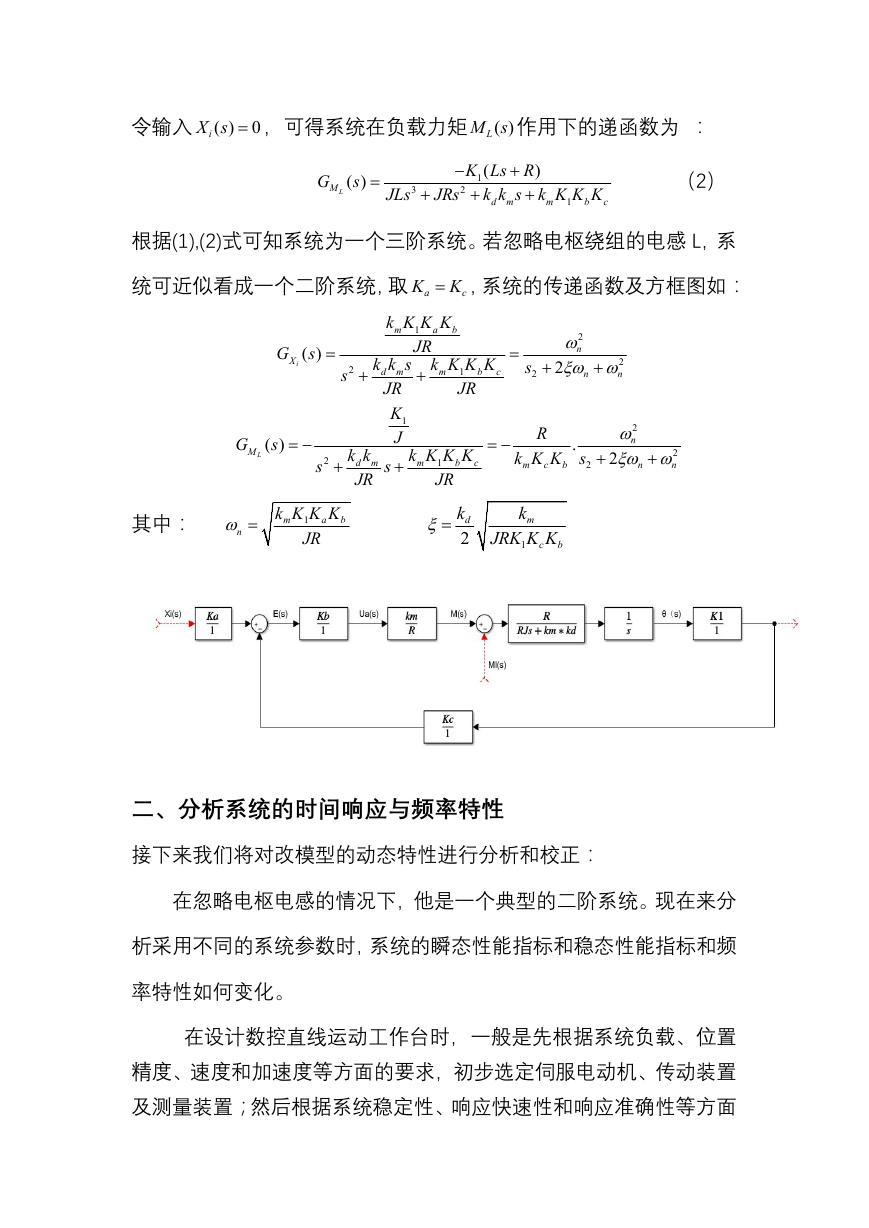
    令输入 ( ) 0 iX s  ，可得系统在负载力矩 ( ) LM s 作用下的递函数为 ： ( ) G s LM   2 JRs K Ls R 1   (  k k s d m 3 JLs  ) k K K K m 1 b （2） c 根据(1),(2)式可知系统为一个三阶系统。若忽略电枢绕组的电感 L，系 统可近似看成一个二阶系统，取 a K K ，系统的传递函数及方框图如： c k K K K m a b 1 JR  k K K K m b 1 JR  c s 2  2  n 2 2   n  n ( ) G s X i  2 s  k k s d m JR K 1 J  s ( ) G s M L   2 s  k k d m JR k K K K m b 1 JR   c R . k K K s m c b 2  n 2 2   n  n  2 其中：   n k K K K 1m a JR b  k d 2 k m JRK K K 1 c b 二、分析系统的时间响应与频率特性 接下来我们将对改模型的动态特性进行分析和校正： 在忽略电枢电感的情况下，他是一个典型的二阶系统。现在来分 析采用不同的系统参数时，系统的瞬态性能指标和稳态性能指标和频 率特性如何变化。 在设计数控直线运动工作台时，一般是先根据系统负载、位置 精度、速度和加速度等方面的要求，初步选定伺服电动机、传动装置 及测量装置；然后根据系统稳定性、响应快速性和响应准确性等方面
    的要求，设计控制器。因此，在分析系统的时域性能指标时，与电动 机有关的参数、与传动部件有关的参数一般是确定的。假设确定传递 方框如下，现在用MATLAB来分析放大器的放大系数K，取不同值时， 系统的性能如何变化。 有方框图可得其开环传递函数和闭环传递函数分别为 ( ) G s k  ( ) G s b  s s 30 K b 2 10 s  30 K b 30 10 s   2 K b 利用 matlab 求瞬态特性的： t = 0:0.001:1; yss = 1;dta = 0.02; k1 =5;num = 20*k1;den = [1 10 30*k1];G1 = tf(num,den); k2 = 16;num = 20*k2;den = [1 10 30*k2];G2 = tf(num,den); k3 = 50;num = 20*k3;den = [1 10 30*k3];G3 = tf(num,den); [y1,t] = step(G1,t); [y2,t] = step(G2,t);[y3,t] = step(G3,t); plot(t,y1,'--',t,y2,'-.',t,y3,'-');grid on; xlabel('t/s'),ylabel('Xo(t)') r =1;while y1(r)1-dta&&y1(s)<1+dta; s = s-1;end
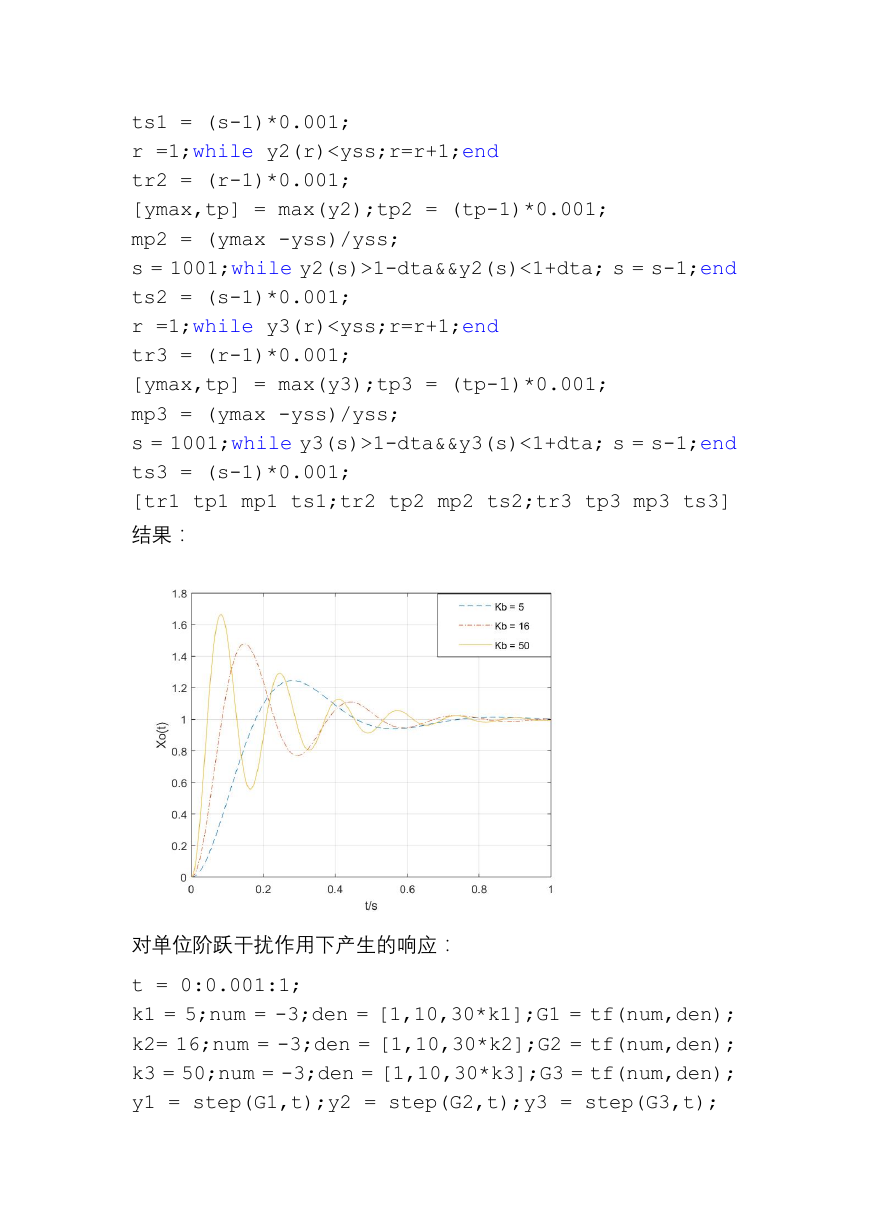
    ts1 = (s-1)*0.001; r =1;while y2(r)1-dta&&y2(s)<1+dta; s = s-1;end ts2 = (s-1)*0.001; r =1;while y3(r)1-dta&&y3(s)<1+dta; s = s-1;end ts3 = (s-1)*0.001; [tr1 tp1 mp1 ts1;tr2 tp2 mp2 ts2;tr3 tp3 mp3 ts3] 结果： 对单位阶跃干扰作用下产生的响应： t = 0:0.001:1; k1 = 5;num = -3;den = [1,10,30*k1];G1 = tf(num,den); k2= 16;num = -3;den = [1,10,30*k2];G2 = tf(num,den); k3 = 50;num = -3;den = [1,10,30*k3];G3 = tf(num,den); y1 = step(G1,t);y2 = step(G2,t);y3 = step(G3,t);
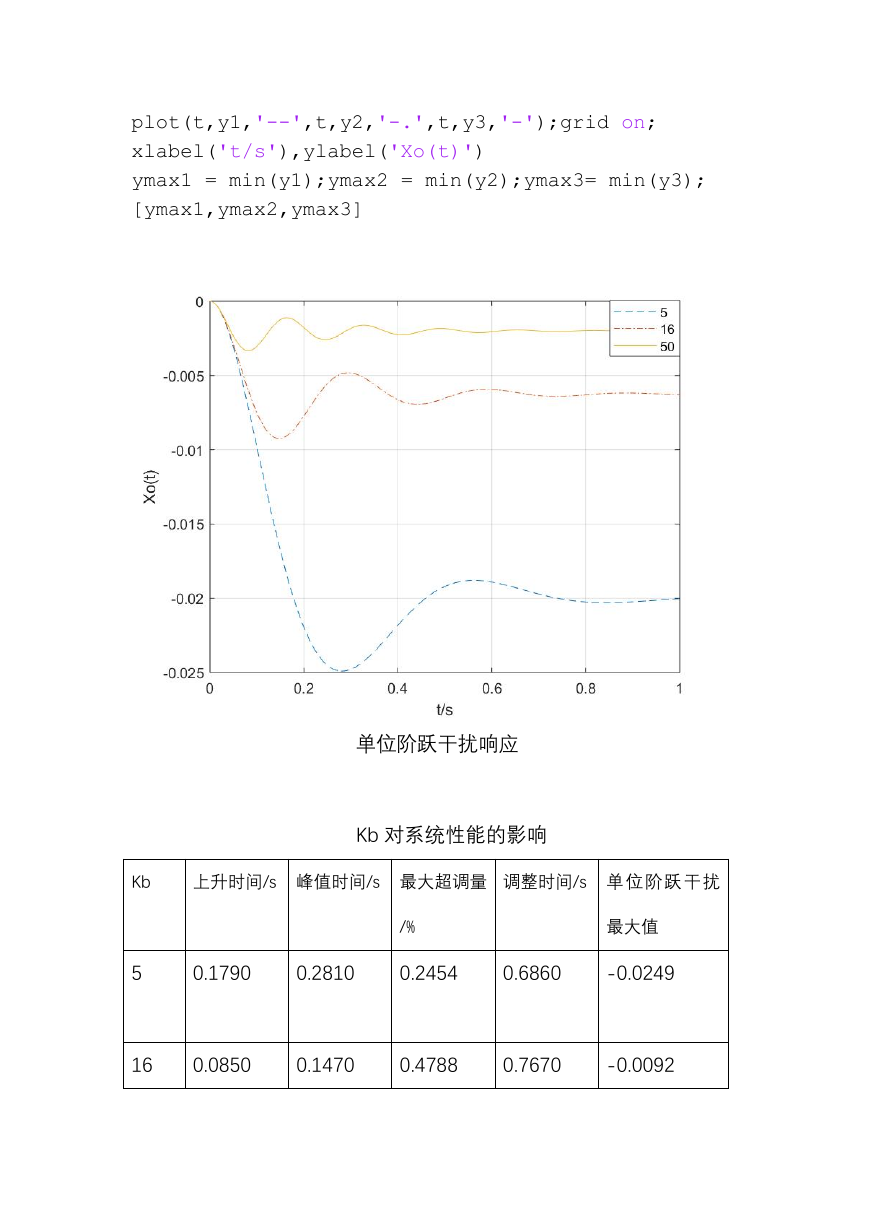
    plot(t,y1,'--',t,y2,'-.',t,y3,'-');grid on; xlabel('t/s'),ylabel('Xo(t)') ymax1 = min(y1);ymax2 = min(y2);ymax3= min(y3); [ymax1,ymax2,ymax3] 单位阶跃干扰响应 Kb 对系统性能的影响 Kb 上升时间/s 峰值时间/s 最大超调量 调整时间/s 单位阶跃干扰 /% 最大值 5 0.1790 0.2810 0.2454 0.6860 -0.0249 16 0.0850 0.1470 0.4788 0.7670 -0.0092
    50 0.0450 0.0820 0.6643 0.7530 -0.0033 由上可知，当 Kb 增大时，系统的上升时间、峰值时间和调整时 间逐渐减少，对单位阶跃干扰的响应最大值（绝对值）减少，而系统 的超调量逐渐增大。这也说明了二阶系统的性能指标存在一定矛盾。 要使二阶系统具有满意的性能指标应选择合适的参数。 分析数控直线运动工作台位置控制系统的频率特性。假设求 Kb = 50 下开环频率特性和闭环频率特性下的 nyquist 图和 bode 图。并 求其频率特性的特征量。 Kb = 50; num = 30*Kb;den1 = [1 10 0];Gk = tf(num,den1); den2 = [1 10 30*Kb]; GB = tf(num,den2); [re1,im1] = nyquist(num,den1); [re2,im2] = nyquist(num,den2); subplot(2,2,1),plot(re1,im1); subplot(2,2,2),plot(re2,im2); w = logspace(-1,3,100); subplot(2,2,3),bode(num,den1); subplot(2,2,4),bode(num,den2); [Gm,Pm,w] = bode(num,den2,w); [Mr, k] = max(Gm); Mr = 20*log10(Mr);Wr = w(k); M0 = 20*log10(Gm(1)); n = 1;while 20*log10(Gm(n))>=-3;n = n+1;end Wb = w(n); [M0,Wb,Wr,Mr]
    开环 Nyquist 闭环 Nyquist Kb = 50 的开环频率特性 bode 图
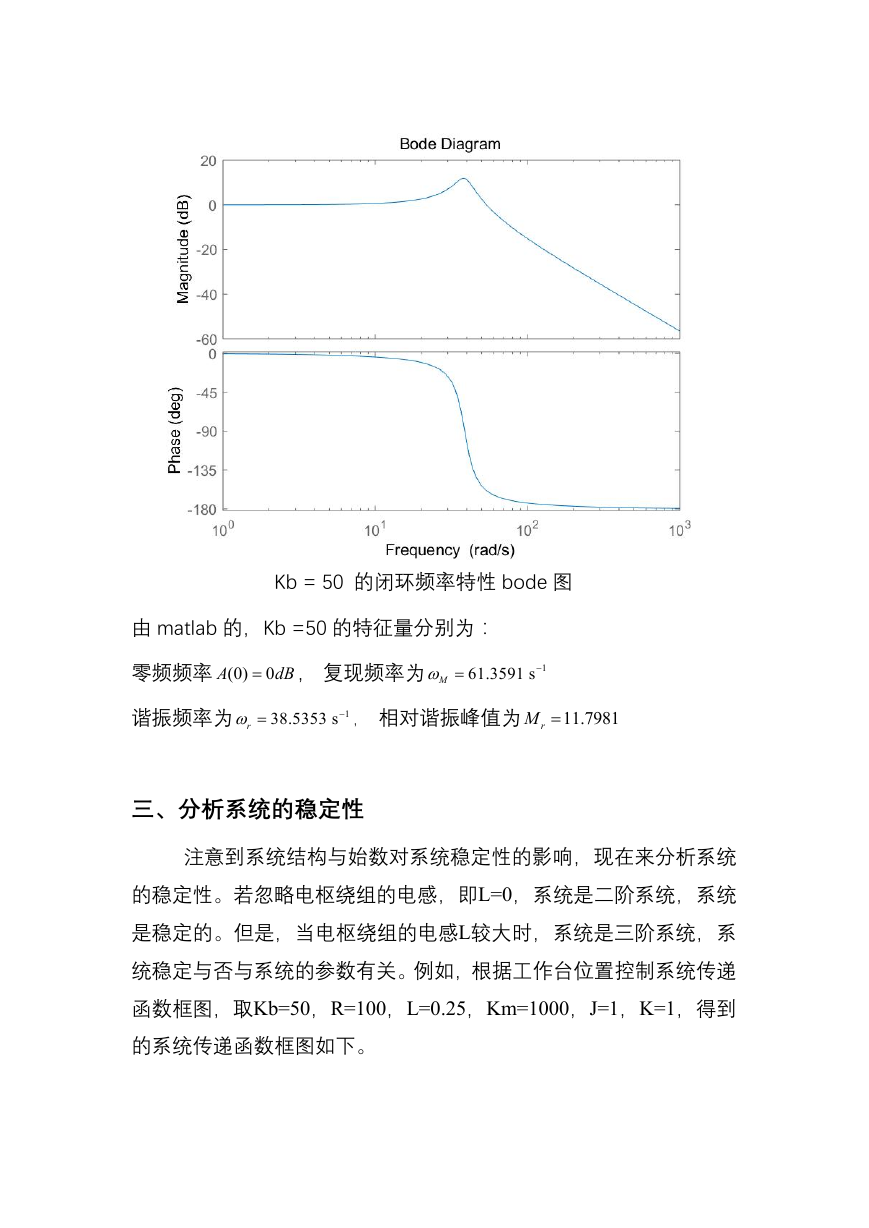
    Kb = 50 的闭环频率特性 bode 图 由 matlab 的，Kb =50 的特征量分别为： 零频频率 (0) A  0 dB , 复现频率为 M  61.3591 s  1 谐振频率为 r  38.5353 s  1 ， 相对谐振峰值为 rM  11.7981 三、分析系统的稳定性 注意到系统结构与始数对系统稳定性的影响，现在来分析系统 的稳定性。若忽略电枢绕组的电感，即L=0，系统是二阶系统，系统 是稳定的。但是，当电枢绕组的电感L较大时，系统是三阶系统，系 统稳定与否与系统的参数有关。例如，根据工作台位置控制系统传递 函数框图，取Kb=50，R=100，L=0.25，Km=1000，J=1，K=1，得到 的系统传递函数框图如下。
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料