logo资料库

基于IMM-UKF 的网络化作战目标跟踪算法.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：1.19M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    收稿日期：2016-08-02修回日期：2016-10-19基金项目：国家自然科学基金资助项目（61472441）作者简介：周中良（1978-），男，江西九江人，副教授。研究方向：多传感器智能信息融合，网络化作战。*摘要：针对网络化作战中单探测节点对机动目标的运动模型不确定性导致滤波精度低，为提高目标跟踪的稳定性和精确性，提出了多节点探测跟踪算法。基于网络体系中信息的共享需求，建立网络探测节点的目标跟踪模型；通过网络探测节点目标跟踪需求和实战要求发现目标经常有多种运动状态并存现象，而单一模型的滤波器不能满足对机动目标跟踪性能的要求。因此，探测节点采用了基于交互式多模型（IMM）的无迹卡尔曼滤波（UKF）算法进行状态估计，融合中心将各节点发送的目标状态估计融合后进行状态估计，有效地降低了目标机动造成的模型误差，提高了跟踪性能。仿真结果表明，所提出的算法提高了网络节点对机动目标的跟踪精度，并且收敛速度快，有较强的鲁棒性和实用性。关键词：网络化作战，机动目标跟踪，网络探测节点，卡尔曼滤波中图分类号：TP391文献标识码：ADOI：10.3969/j.issn.1002-0640.2017.10.021基于IMM-UKF的网络化作战目标跟踪算法*周中良，高智敏，赵彬，刘宏强，郝秦芝（空军工程大学航空航天工程学院，西安710038）Networked-attackTargetTrackingBasedonIMM-UKFAlgorithmZHOUZhong-liang，GAOZhi-min，ZHAOBin，LIUHong-qiang，HAOQin-zhi（SchoolofAeronauticsandAstronauticsEngineering，AirForceEngineeringUniversity，Xi’an710038，China）Abstract：Basedonthenetworkoperationalrequirements，attackarestudiedinthedissertation.Targettrackingmodelofnetworkeddetectionalnodeisbuiltbasedonnetworkinformationsharingrequirement；InteractingMultipleModel（IMM）basedonUnscentedKalmanFilter（UKF）isusedfortargettrackingstateestimationofdetectionnodeandtheactualcombatrequirement，whichfindsthetargetmotionstateisoftenavarietyofcoexistence，thefiltercan’tmeetthesinglemodelformaneuveringtargettrackingperformancerequirements.TheresultshowsthatUKFhaslittleerrorontrackingandithasquicklyconvergencespeedcomparedtotraditionalarithmetic.Keywords：networked-attack，targettracking，networkeddetectionnode，IMM-UKF0引言国外网络中心战理论和网络化作战实践都得到了持续稳步地发展，网络化作战与信息化作战的研究成果非常丰富，理论也日臻成熟。国外的网络化作战技术已经进入工程试验阶段，国内由于研究起步较晚，对网络化作战相关技术的研究还比较薄弱。随着当今技术的发展，各种战机的机动性越来越强，怎样提高网络化攻击高机动目标的跟踪能力成为现代作战的一个重要问题，因此，需要研究更为有效的跟踪滤波方法。现如今目标跟踪技术得到了快速发展和广泛应用［1］，目标跟踪是指通过对传感器获得的原始数据进行处理来解算目标运动要素的信息处理过程［1-2］。根据传感器与目标之间的作用关系，目标跟踪可以分为单传感器单目标跟踪、单传感器多目标跟踪和多传感器多目标跟踪3种典型形式［3］。目前应用最多的两种目标跟踪算法是扩展卡尔曼滤波（EKF）和无迹卡尔曼滤波（UKF），其中UKF以其估计精度较高，且无须计算雅克比矩阵的优点得到更为广泛应用［4］，但EKF、UKF对系统模型的精确度要求比较高，针对EKF、UKF在滤波性能方面的不足，学者们提出了自适应文章编号：1002-0640（2017）10-0097-06Vol.42，No.10Oct，2017火力与指挥控制FireControl&CommandControl第42卷第10期2017年10月97··
    （总第42-）火力与指挥控制2017年第10期滤波方法，文献［5］采用IMM算法融合Sage-Husa自适应滤波器和强跟踪滤波器的优点，解决了系统不确定模型的估计精确性和稳定性问题，但该算法需要计算雅克比矩阵。文献［6］将IMM算法应用于目标导航，有效地提高了单目标的跟踪精度，但该方法只是对系统模型的不确定性提出了解决办法，没有解决多目标带来的不确定性问题，文献［7］提出了随机无迹卡尔曼滤波（RUKF），消除了UKF的系统误差，但在数据丢失的情况下只能实现次优估计，其稳定性较差。目标运动状态的改变将会导致跟踪算法精度降低和发散［8］，针对空中目标运动状态复杂、飞行速度快、环境中扰动不确定、跟踪瞄准难度大，且目标跟踪模型和量测模型几乎都是非线性的问题，本文采取使用交互式多模型（IMM）和无迹卡尔曼滤波器（UKF）相结合的方法，实现系统模型与运动状态匹配，同时利用多探测节点对目标跟踪探测，通过状态融合估计得到一致精确的目标信息，提高了在系统模型不确定条件下对目标的跟踪精度。1网络探测节点目标跟踪模型1.1网络化目标跟踪网络化目标跟踪是指由网络体系内的多个目标探测节点（TDN）共同探测目标，然后通过信息共享和信息融合，形成一致精确的目标信息，如图1所示。网络化目标跟踪是TDN在信息域的组网问题，可以分为单个TDN单目标跟踪、单个TDN多目标跟踪和多个TDN多目标跟踪3种样式［9］。网络探测节点地理位置分散，量测基准、测量方式和量测频率都不尽相同，信息处理和传输相互独立，这些约束对网络化攻击的信息处理提出了严格要求。图1网络化目标跟踪示意图1.2问题描述动态目标的处理需要对所测目标的位置进行连续时间采样的离散测量，同时也要有估计目标运动行为的能力，以预测目标网络探测节点目标跟踪模型的下一位置。这需要将每个新的传感器数据集合与目标航迹的预测位置反复进行关联，以确定哪一个传感器检测是当前的检测或是新目标或是预警［10］。目标跟踪的本质是在目标运动模型的基础上从量测序列｛zi（k）｝中还原目标运动状态x（k）。目标状态模型和量测方程分别表示为：（1）（2）式中，棕（k）和vi（k）都表示为均值为零的白噪声序列，其协方差分别是Qi（k）和Ri（k）。图2目标跟踪基本原理图图2中目标的动态特性是由位置、速度和加速度的状态向量X表示，量测量Y被假定为含有量测噪声V的状态向量的线性组合（匀载垣灾），参差向量d为Y与HX赞（k+1/k）之差。1.3目标跟踪模型的建立建立机动目标模型的基本原则是既要尽可能符合目标的运动实际，又要便于数学处理。目标的数学模型就是把某一个时间点目标的状态变量表征为前一个时间点状态变量的函数，这样才符合滤波理论的递推规则。为方便网络节点的信息融合与共享，需要在统一的基准坐标下建立量测方程。在文中选取描述火力控制问题的通用惯性坐标系（OXYZ）d作为基准［4］，原点取在地球质量中心，Xd轴取子午面与通过原点且同Zd轴正交的赤道面交线，Yd是右手地心地固直角坐标系［11-12］。将（OXYZ）d下T的运动状态记作x，x可以选取目标位置分量，可以选取目标位置和速度分量，也可以目标的位置、速度和加速度分量，而x形式的选择很大程度上取决于作战的需求。设N1、N2和N3分别表示3个网络探测节点（探测平台），T为被探测对象，N1、N2、N3、T之间的关系可以表示为下页图3所示。98··1774
    （总第42-）图3网络化目标跟踪量测示意图由于x是在基准坐标系中（OXYZ）d表达的，zi是在Ni的飞机坐标系下给出的，为了进行状态估计需要建立量测方程。假定N1、N2、N3测量方式一样，在此以N1举例来建立量测方程。设N1获得T的量测信息包括距离r1、方位角u1和俯仰角v1，则取，可得N1对T的量测方程为：（3）在上式中，h（x（k））量测函数，表示为k时刻的量测噪声，v1（k）为互不相关且服从零均值的高斯分布，其协方差为R1（k）。h（x（k））可表示为：（4）2基于IMM-UKF的目标状态估计算法由式（3）可以看出，量测方程是非线性的，那么就需要采用非线性滤波进行状态估计。无迹卡尔曼滤波UKF是一种高效费比的非线性滤波算法［12］，在非线性滤波中得到了广泛应用，不仅计算量小，而且采用递推式滤波，便于计算机编程运算，则本文采用UKF进行状态估计［13］。由于空中目标的运动方式具有多变性，仅靠一个单一的模型难以有效描述目标的运动状态，为此，交互式多模型（IMM）算法就成为一种自然的选择［14-17］。IMM算法是将目标可能的运动模式映射为模型集，采用多个目标运动模型将不同的滤波器并行工作，再将各滤波器的状态估计基于Bayes推理进行融合后输出，从而通过多个运动模型的交互达成自适应修正模型的目的［8］。IMM被证明是一种最有效的混合估计方案，并逐渐成为该领域研究的主流方向［18］。鉴于IMM算法的显著优点，本文将UKF引入到IMM算法中得到IMM-UKF算法，并采用该算法进行目标状态估计。图4交互式多模型结构图IMM-UKF在滤波前需要进行如下初始条件设置：设定机动模型集和模型的初始概率为和概率转移矩阵∏m×m，给定滤波初始状态x赞（0/0）和P（0/0）。IMM算法是递推式的，主要由模型条件重初始化、模型条件滤波、模型概率更新和组合输出4个步骤组成：Step.1模型条件重初始化：设时刻k，模型的概率为个模型的转移概率矩阵为：（5）模型i的预测概率为：（6）模型i混合状态估计为：（7）模型i混合协方差估计为：（8）Step.2模型条件滤波。对模型i基于x赞0i（k|k）和P赞0i（k|k）进行UKF递推估计：周中良，等：基于IMM-UKF的网络化作战目标跟踪算法99··1775
    （总第42-）火力与指挥控制2017年第10期①构造Sigma点（9）（10）（11）②时间更新（12）③量测更新（13）④状态更新（14）Step.3模型概率更新模型i的似然函数为：（15）式中，。模型i的更新概率为：（16）Step.4组合输出状态混合估计为：（17）协方差混合估计为：（18）网络化作战以网络体系中的多个探测节点共同探测目标，通过状态融合得到一致精确的目标信息，为此，以N1和N2两个探测节点状态融合估计为例给出状态融合流程如图5所示。各探测节点向融合中心提供局部预测状态和更新状态，由融合中心仅融合估计，为了保证状态预测的一致性，融合中心同样采用IMM算法进行融合估计，同时采用与节点相同的模型集进行状态递推估计，再将最新的融合状态反馈给N1和N2，N1和N2基于融合状态进行新的状态预测和状态更新。3算例分析为了验证IMM-UKF算法的有效性，以3个网络探测节点N1、N2、N3对目标T进行跟踪为例进行图5状态融合流程图100··1776
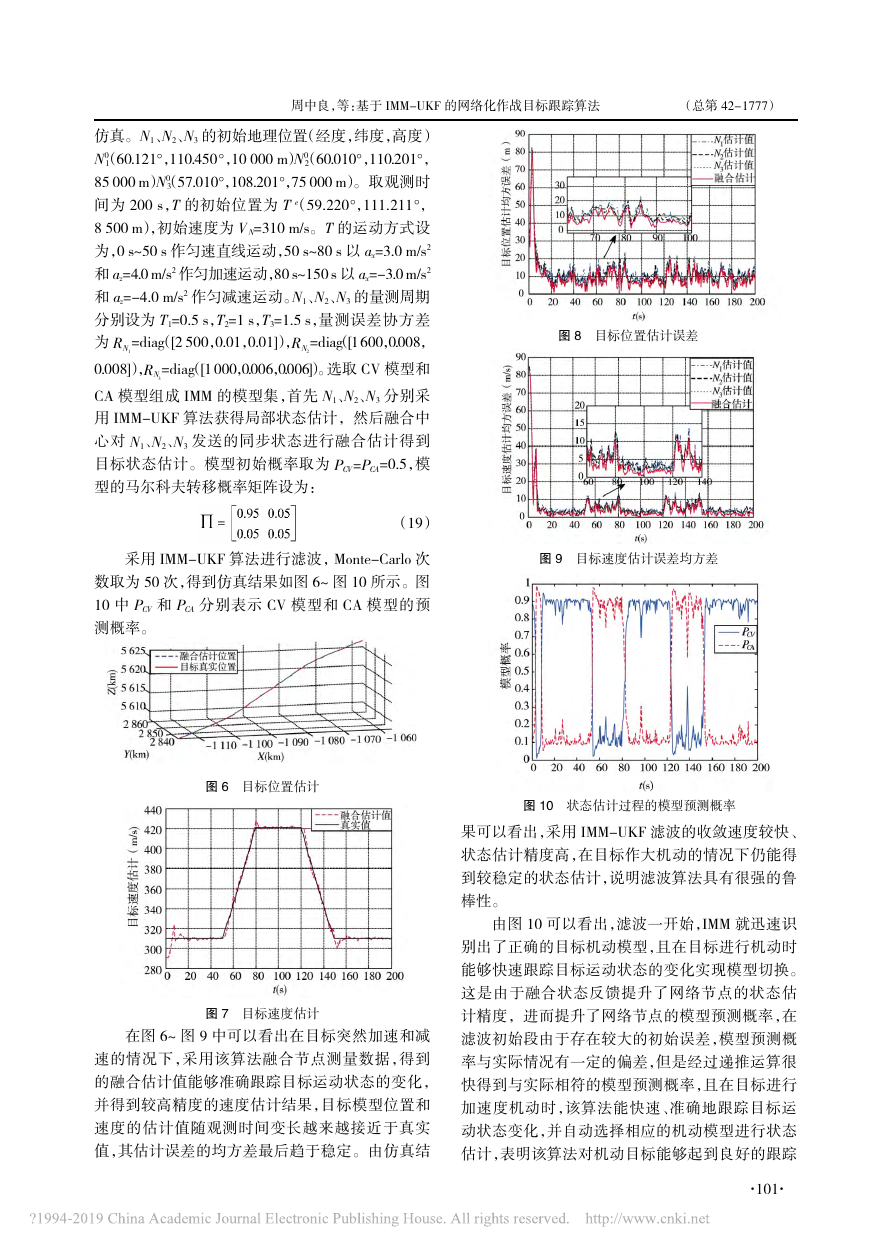
    （总第42-）仿真。N1、N2、N3的初始地理位置（经度，纬度，高度）N01（60.121毅，110.450毅，10000m）N02（60.010毅，110.201毅，85000m）N03（57.010毅，108.201毅，75000m）。取观测时间为200s，T的初始位置为Te（59.220毅，111.211毅，8500m），初始速度为VN=310m/s。T的运动方式设为，0s~50s作匀速直线运动，50s~80s以ax=3.0m/s2和az=4.0m/s2作匀加速运动，80s~150s以ax=-3.0m/s2和az=-4.0m/s2作匀减速运动。N1、N2、N3的量测周期分别设为T1=0.5s，T2=1s，T3=1.5s，量测误差协方差为RN1=diag（[2500，0.01，0.01]），RN2=diag（[1600，0.008，0.008]），RN3=diag（[1000，0.006，0.006]）。选取CV模型和CA模型组成IMM的模型集，首先N1、N2、N3分别采用IMM-UKF算法获得局部状态估计，然后融合中心对N1、N2、N3发送的同步状态进行融合估计得到目标状态估计。模型初始概率取为PCV=PCA=0.5，模型的马尔科夫转移概率矩阵设为：（19）采用IMM-UKF算法进行滤波，Monte-Carlo次数取为50次，得到仿真结果如图6~图10所示。图10中PCV和PCA分别表示CV模型和CA模型的预测概率。图6目标位置估计图7目标速度估计在图6~图9中可以看出在目标突然加速和减速的情况下，采用该算法融合节点测量数据，得到的融合估计值能够准确跟踪目标运动状态的变化，并得到较高精度的速度估计结果，目标模型位置和速度的估计值随观测时间变长越来越接近于真实值，其估计误差的均方差最后趋于稳定。由仿真结果可以看出，采用IMM-UKF滤波的收敛速度较快、状态估计精度高，在目标作大机动的情况下仍能得到较稳定的状态估计，说明滤波算法具有很强的鲁棒性。由图10可以看出，滤波一开始，IMM就迅速识别出了正确的目标机动模型，且在目标进行机动时能够快速跟踪目标运动状态的变化实现模型切换。这是由于融合状态反馈提升了网络节点的状态估计精度，进而提升了网络节点的模型预测概率，在滤波初始段由于存在较大的初始误差，模型预测概率与实际情况有一定的偏差，但是经过递推运算很快得到与实际相符的模型预测概率，且在目标进行加速度机动时，该算法能快速、准确地跟踪目标运动状态变化，并自动选择相应的机动模型进行状态估计，表明该算法对机动目标能够起到良好的跟踪图10状态估计过程的模型预测概率图8目标位置估计误差图9目标速度估计误差均方差周中良，等：基于IMM-UKF的网络化作战目标跟踪算法101··1777
    （总第42-）火力与指挥控制2017年第10期（上接第96页）［4］金瑶兰，渠立鹏，章敏莹.射流管伺服阀AMESim建模与仿真［J］.液压气动与密封，2010，34（8）：45-47.［5］SOMASHEKHARSH，SINGAPERUMALM，KRISHNAKU-MARR.Modellingthesteady-stateanalysisofajetpipeelec-trohydraulicservovalve.Proc.InstnMech.Engrs，PartI［J］.SystemsandControlEngineering，2006，220（12）：109-129.［6］马小良.偏导射流电液伺服阀工程化建模及仿真研究［J］.液压与气动，2015，39（3）：83-85.［7］王春行.液压控制系统［M］.北京：机械工业出版社，2005.［8］上海七〇四研究所衡拓实业发展有限公司伺服阀部.射流管电液伺服阀专题讲座［J］.液压与气动，2009，33（9）：88-89.［9］王传礼.基于GMN转换器喷嘴挡板阀的研究［D］.杭州：浙江大学，2005.［10］宋志安，曹连民，黄靖.MATLAB/Simulink与液压控制系统仿真［M］.北京：国防工业出版社，2012.效果。4结论本文运用CV和CA目标机动模型，针对网络化作战中单探测节点对机动目标的运动模型的不确定性导致滤波精度低的问题，将IMM引入到UKF算法中得到IMM-UKF用于跟踪滤波，为提高目标跟踪的稳定性和精确性，提出了通过对3个节点的状态估计进行融合提高对目标的跟踪精度，克服了传统滤波器容易产生发散的问题，改善了滤波性能，提高了网络化攻击模型算法的精确度，在目标作大机动的情况下仍能得到较稳定的状态估计，具有很强的鲁棒性，由于算法计算量较少使算法整体具有很快的收敛速度，同时采用多节点探测避免了单节点被干扰导致跟踪误差大甚至丢失的情况出现，使整个网络系统具有良好的抗干扰能力等。网络化作战中，目标跟踪只是其中的一个方面，只有在具备良好的目标跟踪能力的基础上，导引武器系统完成火力打击，才能有效地完成作战任务，所以下一步将解决多节点协同导引，提高导弹的命中率。参考文献：［1］付昭旺.战斗机对空网络化攻击火控关键技术研究［D］.西安：空军工程大学，2013.［2］石章松.目标跟踪与数据融合理论及方法［M］.北京：国防工业出版社，2010.［3］BLOMHAP，BAR-SHALOMY.Theinteractingmultiplemodelalgorithmforsystemswithmarkovianswitchingcoefficients［J］.IEEETrans.onAutomaticControl，1988，33（8）：780-783.［4］王康，刘莉，杜小菁，等.基于UKF的GPS定位算法［J］.宇航学报，2011，32（4）：795-801.［5］MALLESWARANM，VAIDENHIV，IRWINS，etal.IMM-UKF-TFSmodel-basedapproachforintelligentnavi-gation［J］.JournalofNavigation，2013，66（6）：859-877.［6］DUNIKJ，STRAKAO，SIMANDLM.ThedevelopmentofarandomizedunscentedKalmanfilter［C］//Proceedingsofthe18thIFACWordCongress.NewYork：CuranAssociatesInc，2011：8-13.［7］杨永建，樊晓光，王晟达，等.基于自适应CS模型的IMM算法［J］.系统工程与电子技术，2016，38（5）：977-983.［8］亲永元，张洪钺，汪叔华，等.卡尔曼滤波与组合导航原理［M］.西安：西北工业大学出版社，2012.［9］FISHERKA，MAYBECKPS.Multiplemodeladaptiveestimationwithfilterspawning［J］.TransactionsonAerospaceandElectronicSystems，2002，38（4）：1311-1322.［10］魏子卿.大地坐标系新探［J］.武汉大学学报（信息科学版），2011，36（8）：883-886.［11］陈俊勇.中国现代大地基准：中国大地坐标系统2000（CGCS2000）及其框架［J］.测绘学报，2008，37（3）：268-271.［12］JIANGBA，WANQ.ManeuveringtargetpassivetrackingwithdualinfraredobserversusingIMMalgorithmbasedonUKF［J］.SystemsEngineeringandElectronics，2008，30（8）：1454-1459.［13］李理敏，龚文斌，刘会杰，等.基于自适应扩展卡尔曼滤波的载波跟踪算法［J］.航空学报，2012，33（7）：1319-1328.［14］WONJH，EISSFELLERB.Atuningmethodbasedonsig-nal-to-noisepowerratioforadaptivePLLanditsrelation-shipwithequivalentnoisebandwidth［J］IEEECommuni-cationsLetters，2013，17：393-396.［15］WANEA，VANDERMERWER.Theunscentedkalmanfilterfornonlinearestimation［C］//ProceedingoftheIEEESymposium2000onAdaptiveSystemsforSignalProcessing，CommunicationandControl，2000.［16］李洋，杜立夫，禹春梅.一种基于复合模型的机动目标跟踪算法［J］.四川兵工学报，2015，36（5）:127-132.［17］沈锋，贺瑞，吕东泽，等.基于卡尔曼滤波器的高动态GPS载波跟踪环［J］.宇航学报，2012，33（8）：1041-1047.［18］DANSIMON.OptimalStateestimation［M］.NewYork：WileyInterScience，2006.102··1778
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料