logo资料库

自动控制原理课程设计 PID控制的倒立摆.docx

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.34M 资料格式：docx 举报 版权申诉
第1页 / 共15页
第2页 / 共15页
第3页 / 共15页
第4页 / 共15页
第5页 / 共15页
第6页 / 共15页
第7页 / 共15页
第8页 / 共15页
资料共15页，剩余部分请下载后查看
    一、引 言
    二、一阶倒立摆控制系统及其工作原理
    三、建立一阶倒立摆控制系统模型
    3.1.一阶倒立摆建模
    3.2、一阶倒立摆特性
    3.3电动机驱动器
    四、双闭环PID控制器设计
    4.1内环控制器的设计
    4.2 外环控制器的设计
    五、系统的simulink仿真
    六、课程设计总结
    七、参考文献
    基于双闭 PID 控制的一阶倒立摆系统
    1 摘 要 直线一级倒立摆，是由沿直线导轨运动的小车以及一端固定于小车的匀质长杆组成的非 线性的、不稳定的系统。 本文主要讲了采用机理建模的方法得到一阶倒立摆的数学模型，并采用 PID 双闭环控制 的方式来控制它，从而使其成为稳定的系统，并对整个过程进行了 matlab 仿真分析。 关键字：一级倒立摆 PID 控制器 双闭环 matlab 仿真 Abstract First-order linear inverted pendulum is composed of a trolley, moved along the linear guides, and a homogeneous pole, one end of which is fixed at the car. However, this system is non-linear and unstable. This article stresses the use of modeling approach to the mechanism of first-order mathematical model of the inverted pendulum, and the use of double-loop PID control to control it, making it a stable system, and the whole process simulation analysis with MATLAB. Keywords: Linear inverted pendulum PID controller double-loop MATLAB simulation
    2 目录 一、引 言 ..................................................... 3 二、一阶倒立摆控制系统及其工作原理 ............................. 4 三、建立一阶倒立摆控制系统模型 ................................. 4 3.1 一阶倒立摆建模 ....................................................... 4 3.2 一阶倒立摆特性 ....................................................... 6 3.3 电动机驱动器 ......................................................... 7 四、双闭环 PID 控制器设计 ....................................... 7 4.1 内环控制器的设计 ..................................................... 7 4.2 外环控制器的设计 .................................................... 10 五、系统的 simulink 仿真 ....................................... 13 六、课程设计总结 ............................................. 14 七、参考文献 ................................................. 14
    3 一、引 言 倒立摆系统是一个非线性自然不稳定系统，是进行控制理论教学 及开展各种控制实验的理想实验平台．许多抽象的控制概念，如控制 系统的稳定性、可控性、系统抗干扰能力等，都可以通过倒立摆系统 直观地表现出来．除教学用途外，倒立摆系统的高阶次、不稳定、多 变量、非性和强耦合等特性，使得许多现代控制理论的研究人员一直 将它视为研究对象．他们不断从研究倒立摆控制方法中发掘出新的控 制方法，并将其应用于航天科技和机器人学等高新科技领域．倒立摆 系统是典型的机电一体化系统，其机械部分遵循牛顿的力学定律，其 电气部分遵守电磁学的基本定理．因此，可以通过机理建模方法得到 较为准确的系统数学模型，通过实际测量和实验来获取系统模型参 数．无论哪种类型的倒立摆系统，都具有3个特性，即：不确定性、 耦合性、开环不稳定性．直线型倒立摆系统，是由沿直线导轨运动的 小车以及一端固定于小车上的匀质长杆组成的系统．小车可以通过传 动装置由交流伺服电机驱动．小车导轨般有固定的行程，因而小车的 运动范围是受到限制的．
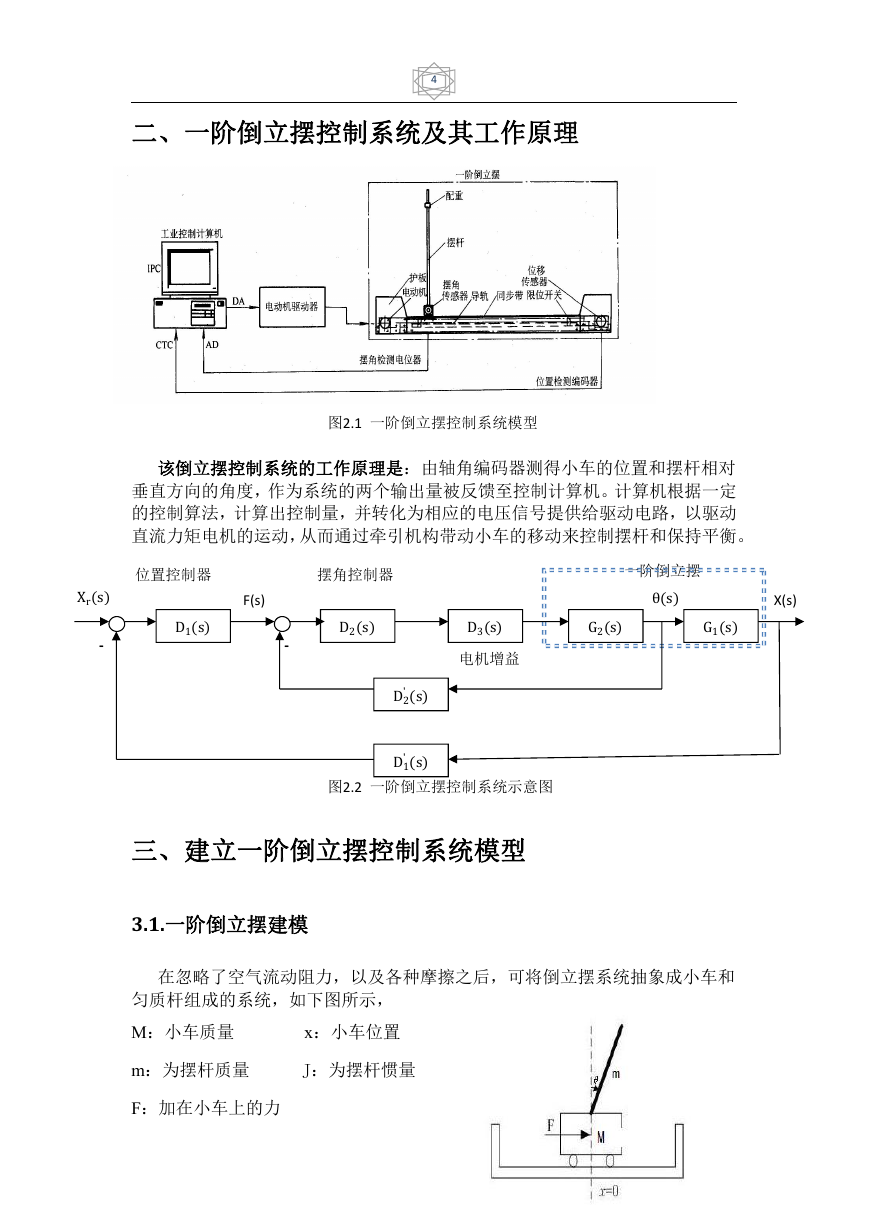
    4 二、一阶倒立摆控制系统及其工作原理 图2.1 一阶倒立摆控制系统模型 该倒立摆控制系统的工作原理是：由轴角编码器测得小车的位置和摆杆相对 垂直方向的角度，作为系统的两个输出量被反馈至控制计算机。计算机根据一定 的控制算法，计算出控制量，并转化为相应的电压信号提供给驱动电路，以驱动 直流力矩电机的运动，从而通过牵引机构带动小车的移动来控制摆杆和保持平衡。 Xr(s) - 位置控制器 摆角控制器 D1(s) F(s) - D2(s) D3(s) 电机增益 一阶倒立摆 θ(s) G2(s) G1(s) X(s) D2'(s) D1'(s) 图2.2 一阶倒立摆控制系统示意图 三、建立一阶倒立摆控制系统模型 3.1.一阶倒立摆建模 在忽略了空气流动阻力，以及各种摩擦之后，可将倒立摆系统抽象成小车和 匀质杆组成的系统，如下图所示， M：小车质量 x：小车位置 m：为摆杆质量 J：为摆杆惯量 F：加在小车上的力
    5 l ：摆杆转动轴心到杆质心的长度 θ：摆杆与垂直向上方向的夹角 根据牛顿运动定律以及刚体运动规律，可知： （1） 摆杆绕其重心的转动方程为  J   F l y sin   F l x cos ..........(1)  （2） 摆杆重心的运动方程为 F m x  2 d 2 d t ( x  l sin )..........(2)  F mg m y   2 d 2 d t ( cos ).........(3) l  （3）小车水平方向上的运动为 F F M   x 2 d x 2 d t ..........(4) 联立上述 4 个方程，可以得出 一阶倒立摆数学模型：    2 J ml F ml J ml sin cos   lgsin   x            2   2  2 sin .        2 2 J ml M m m l     2 2 2 sin cos . F m l    2 2 2 m l    2 2 m l g 2 cos   M m m   M m J ml    cos  2 ml cos .  式中 J 为摆杆的转动惯量： J  2ml 3 若只考虑θ在其工作点附近θ0=0 附近（   10   10  ）的细微变化，则可 以近似认为：   2  sin   cos  0    1   .. x    ..       ( ( 2 ) J  ( mMJ mmM ( mMJ 22 glmFml   2 ) Mml  lg   ) Mml  mlF 2  )   若取小车质量 M=2kg,摆杆质量 m=1kg,摆杆长度 2 l =1m,重力加速度取
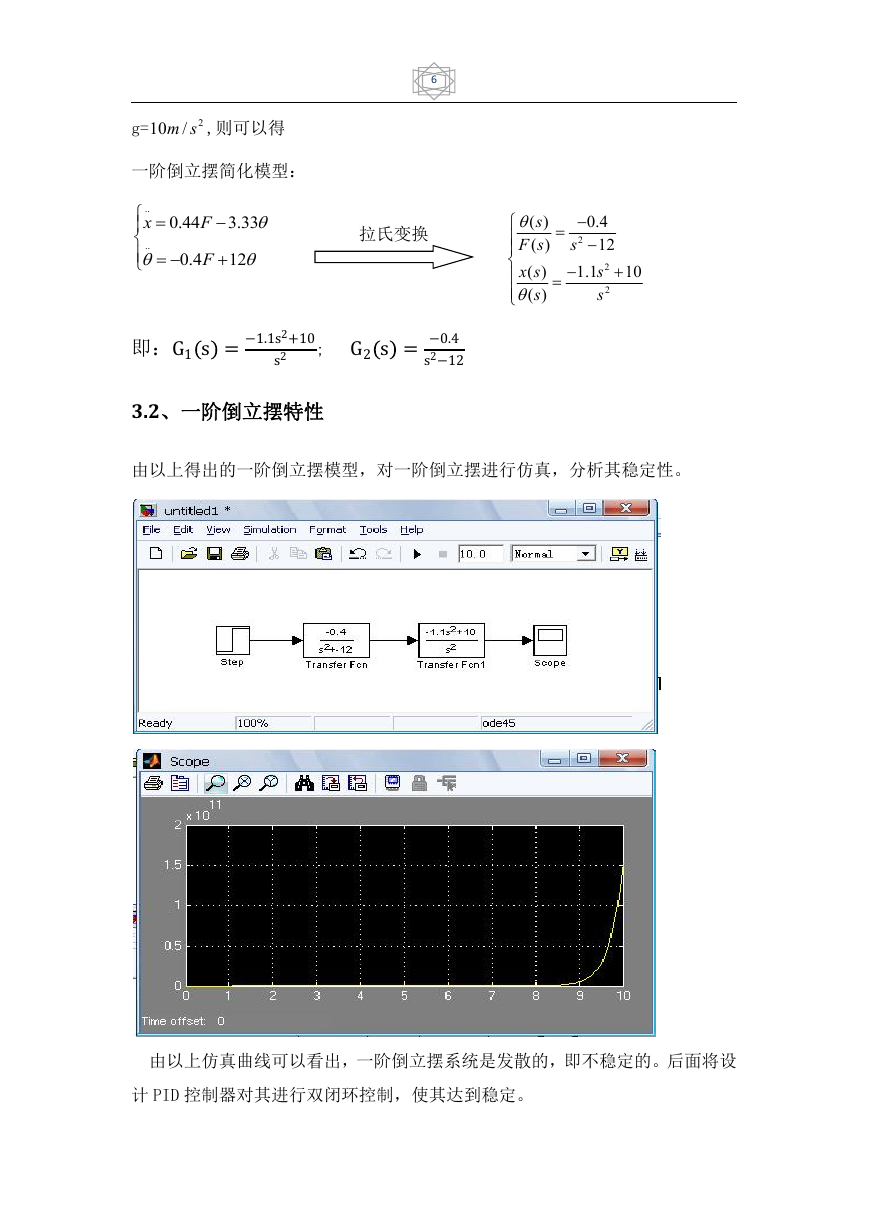
    6 g= 10 / sm 2 ,则可以得 一阶倒立摆简化模型： 0.44 F  3.33  拉氏变换 ..   x   ..      0.4 F  12  即：G1s =−1.1s2+10 s2 3.2、一阶倒立摆特性 ; G2s = −0.4 s2−12 ( ) s    ( ) F s   ( ) x s   ( ) s     2 0.4 12 s  2 1.1 s   s 2 10 由以上得出的一阶倒立摆模型，对一阶倒立摆进行仿真，分析其稳定性。 由以上仿真曲线可以看出，一阶倒立摆系统是发散的，即不稳定的。后面将设 计 PID 控制器对其进行双闭环控制，使其达到稳定。
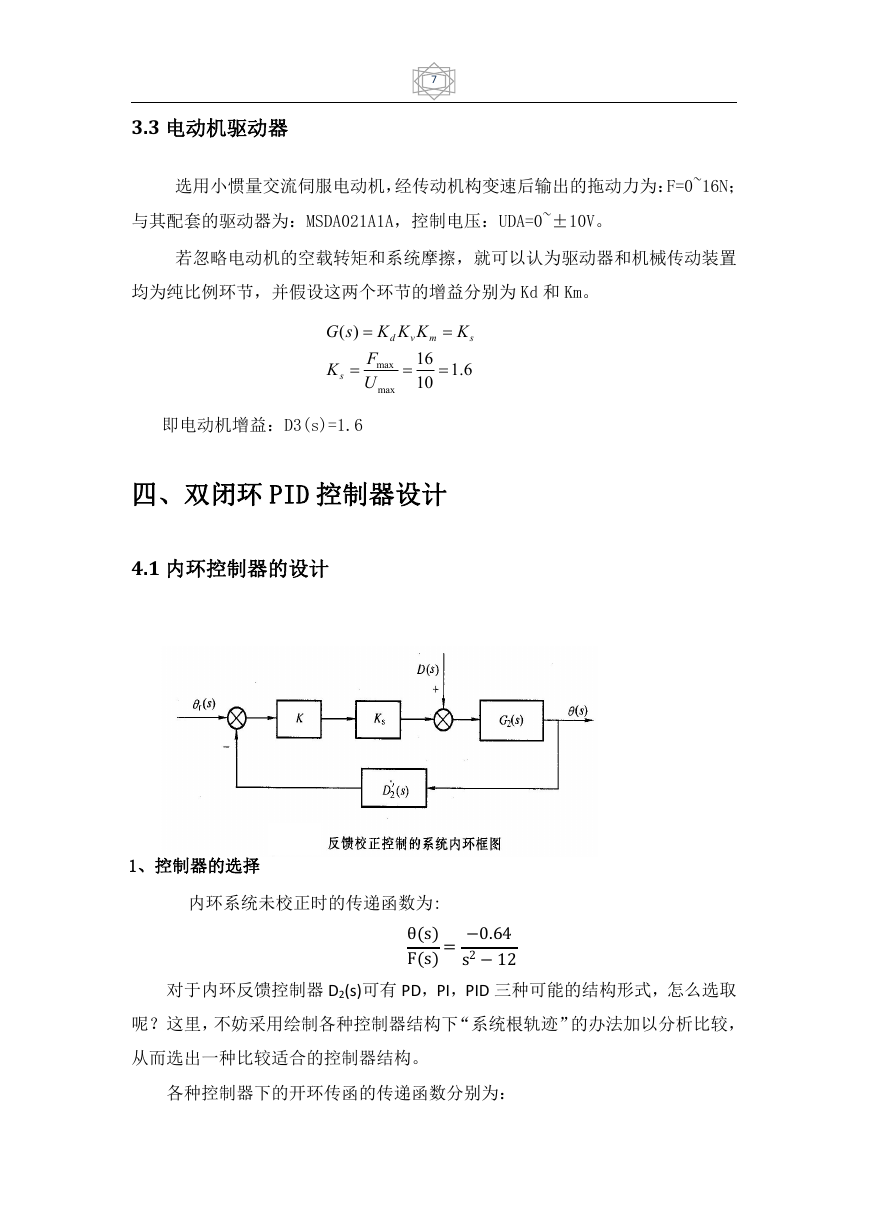
    3.3 电动机驱动器 7 选用小惯量交流伺服电动机，经传动机构变速后输出的拖动力为：F=0~16N； 与其配套的驱动器为：MSDA021A1A，控制电压：UDA=0~±10V。 若忽略电动机的空载转矩和系统摩擦，就可以认为驱动器和机械传动装置 均为纯比例环节，并假设这两个环节的增益分别为 Kd 和 Km。 )( sG K s  KKK  mv 16 F max 10 U  d max  K s  6.1 即电动机增益：D3(s)=1.6 四、双闭环 PID 控制器设计 4.1 内环控制器的设计 其中，Ks=1.6 为伺服电动机与减速机构的等效模型 1、控制器的选择 内环系统未校正时的传递函数为:θ(s)F(s)=−0.64 s2−12 对于内环反馈控制器 D2(s)可有 PD，PI，PID 三种可能的结构形式，怎么选取 呢？这里，不妨采用绘制各种控制器结构下“系统根轨迹”的办法加以分析比较， 从而选出一种比较适合的控制器结构。 各种控制器下的开环传函的传递函数分别为：
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料