LDA数学八卦.pdf

发布时间：2022-05-31 发布人：admin 分类：说明书资料大小：1.94M 资料格式：pdf 举报版权申诉

weixin_43169921-11851672-4744300845376286890.pdf-第1页.png

第1页 / 共55页

weixin_43169921-11851672-4744300845376286890.pdf-第2页.png

第2页 / 共55页

weixin_43169921-11851672-4744300845376286890.pdf-第3页.png

第3页 / 共55页

weixin_43169921-11851672-4744300845376286890.pdf-第4页.png

第4页 / 共55页

weixin_43169921-11851672-4744300845376286890.pdf-第5页.png

第5页 / 共55页

weixin_43169921-11851672-4744300845376286890.pdf-第6页.png

第6页 / 共55页

weixin_43169921-11851672-4744300845376286890.pdf-第7页.png

第7页 / 共55页

weixin_43169921-11851672-4744300845376286890.pdf-第8页.png

第8页 / 共55页

0.1 开篇

0.2 神奇的Gamma 函数

0.2.1 Gamma 函数诞生记

0.2.2 Gamma 函数欣赏

0.2.3 从二项分布到Gamma 分布

0.3 认识Beta/Dirichlet 分布

0.3.1 撒旦的游戏——认识Beta 分布

0.3.2 Beta-Binomial 共轭

0.3.3 Dirichlet-Multinomial 共轭

0.3.4 Beta/Dirichlet 分布的一个性质

0.4 MCMC 和Gibbs Sampling

0.4.1 随机模拟

0.4.2 马氏链及其平稳分布

0.4.3 Markov Chain Monte Carlo

0.4.4 Gibbs Sampling

0.5 文本建模

0.5.1 Unigram Model

0.5.2 Topic Model 和PLSA

0.6 LDA 文本建模

0.6.1 游戏规则

0.6.2 物理过程分解

0.6.3 Gibbs Sampling

0.6.4 Training and Inference

0.7 后记

LDA Œ˘l% Rickjin(@), version 1.0 2013 c 2 8 F

Contents 0.1 m . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0.2 Gamma…Œ . . . . . . . . . . . . . . . . . . . . . . . . . . 0.2.1 Gamma …Œ)P . . . . . . . . . . . . . . . . . . . . . 0.2.2 Gamma …Œ! . . . . . . . . . . . . . . . . . . . . . . 0.2.3 l'Gamma ' . . . . . . . . . . . . . . . . . 0.3 @£Beta/Dirichlet' . . . . . . . . . . . . . . . . . . . . . . . 0.3.1 giZ—@£Beta ' . . . . . . . . . . . . . . . . . 0.3.2 Beta-Binomial . . . . . . . . . . . . . . . . . . . . . 0.3.3 Dirichlet-Multinomial . . . . . . . . . . . . . . . . . 0.3.4 Beta/Dirichlet '5 . . . . . . . . . . . . . . . 0.4 MCMC Gibbs Sampling . . . . . . . . . . . . . . . . . . . . . . 0.4.1 ¯[ . . . . . . . . . . . . . . . . . . . . . . . . . . . 0.4.2 Œ…9†›' . . . . . . . . . . . . . . . . . . . . . 0.4.3 Markov Chain Monte Carlo . . . . . . . . . . . . . . . . . 0.4.4 Gibbs Sampling . . . . . . . . . . . . . . . . . . . . . . . . 0.5 ' . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0.5.1 Unigram Model . . . . . . . . . . . . . . . . . . . . . . . . 0.5.2 Topic Model PLSA . . . . . . . . . . . . . . . . . . . . 0.6 LDA ' . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0.6.1 iZ5K . . . . . . . . . . . . . . . . . . . . . . . . . . . 0.6.2 nL§') . . . . . . . . . . . . . . . . . . . . . . . . . 0.6.3 Gibbs Sampling . . . . . . . . . . . . . . . . . . . . . . . . 0.6.4 Training and Inference . . . . . . . . . . . . . . . . . . . . 0.7 P . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 2 7 10 13 13 17 21 24 24 24 27 31 34 37 38 42 44 44 46 49 52 53 1

0.1 m 3Machine Learning ¥§LDA ·~^.{¡Linear Discrim- inant Analysis Latent Dirichlet Allocation§3ø'¥•l% ·" LDA ·3'¥Ø˝¶.§aquSVD, PLSA .§–^uf´',3'´'¥·Øk^." Ø3 ·§ø.¥9Œ˘£k:ı§)Gamma …Œ§Dirichlet '§ Dirichlet-Multinomial §Gibbs Sampling, Variational Inference, d' §PLSA , –9LDA '" ø'8I§·˚3˘Sn)LDA .¥§I) ›Œ˘£" ·g,?n!¯˘S!Œ §§ˆø˚§IŒ˘˜:£˜LFWk) 5V˙ŒnO6ø" 'IK!/l%0i§ˇl%¿Xgd!!–UŒ1 §[!?nJk>/¶,•F"l%·ØN·n)§ =Bƒ·’uŒ˘l%" Øu'¥?§Hu&•#L˘ Ærickjin, ‰·ezhihuijin@gmail.com" 0.2 Gamma…Œ 0.2.1 Gamma …Œ)P ∞ ˘pŒ˘§•˘SLXek:AGamma…Œ Γ(x) = tx−1e−tdt ˇL'¨'{§–ø…ŒkXe485 0 Γ(x + 1) = xΓ(x) u·ØN·y†§Γ(x) …Œ–⁄·ƒ3¢Œ8§kXe5 Γ(n) = (n − 1)! ˘SGamma …Œ§ıc–5•kƒﬂ 1. øøo%…Œ§Œ˘[·XØ¶ 2. ‰ ´Γ … Œ § ƒ ø … Œ ‰ ´ vΓ(n) = n! ·Γ(n) = (n − 1)! 2

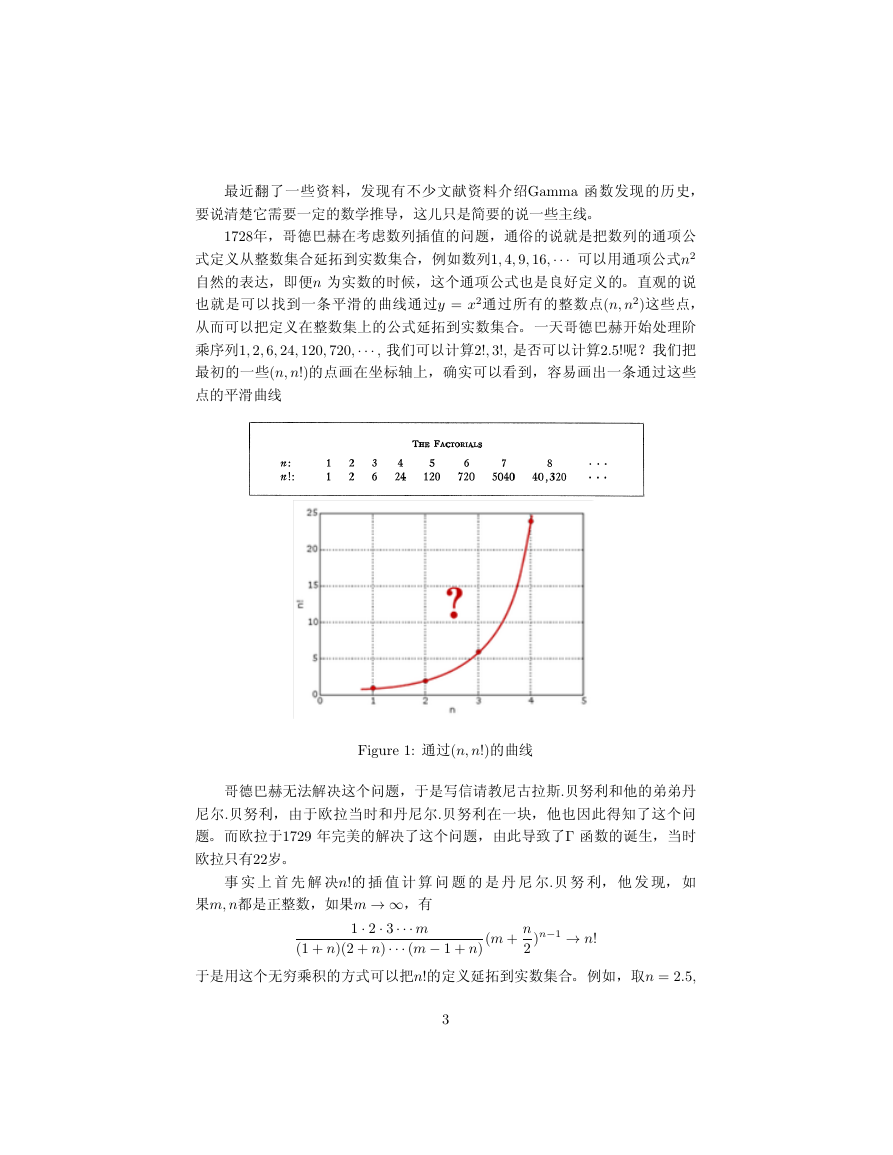
C]§uyk'z]0Gamma …Œuy{⁄§ ‘§I‰Œ˘§ø·{‘" 1728c§xn3˜ŒﬂK§ˇ‘·rŒˇœ “‰´lŒ8¢Œ8§~XŒ1, 4, 9, 16,··· –^ˇœ“n2 g,L§=Bn ¢Œ§øˇœ“·ß—‰´" *‘ ·–Ø^†w›ˇLy = x2ˇL⁄kŒ:(n, n2)ø:§ l–r‰´3Œ8œ“¢Œ8" Uxnm'?n ƒS1, 2, 6, 24, 120, 720,··· , •–O2!, 3!, ·˜–O2.5!Q”•r —(n, n!):x3I¶§(¢–w§N·x^ˇLø :†w› Figure 1: ˇL(n, n!)› xnˆ{)ßøﬂK§u·&Z.d.ª|ƒ33ß Z.ª|§du.ßZ.ª|3‹§ƒˇdøﬂ K".u1729 c{)ßøﬂK§ddΓ …Œ)§ .k22" ﬂ ¢ ˜ k ) ßn! O ﬂ K · ß Z . ª |§ ƒ u y§ X Jm, n·Œ§XJm → ∞§k 1 · 2 · 3··· m (1 + n)(2 + n)··· (m − 1 + n) (m + )n−1 → n! n 2 u·^øˆ¡ƒ¨“–rn!‰´¢Œ8"~X§n = 2.5, 3

m v§˜u“–CqO2.5!" .,uyn! –^Xeˆ¡ƒ¨L 2 n 3 n 1 4 n 2 3 1 n + 1 2 n + 2 3 n + 3 ^4/“§ø“fn– ··· = n! 1 · 2 · 3··· m (1 + n)(2 + n)··· (m + n) lim m→∞ (m + 1)n = n! >–n 1 · 2 · 3··· m (1 + n)(2 + n)··· (m + n) (m + 1)n =1 · 2 · 3··· n · (n + 1)(n + 2)m (1 + n)(2 + n)··· m · (m + 1)n (m + 1)(m + 2)··· (m + n) (1) (2) (m + 1)n (m + 1)(m + 2)··· (m + n) m + 1 m + k → n! (m → ∞) =n! =n! n k=1 ⁄–(1)!(2)“⁄Æ" .m'}`l{~fm'O§ww·˜k5˘§ .4Œ˘*8B" n = 1/2 §\(1)“O§n – 1 ! = 2 · 4 3 · 3 · 4 · 6 5 · 5 · 6 · 8 7 · 7 · 8 · 10 9 · 9 ··· ›y = x(1 − x) e¡¨(·»1¡¨)§’ ,m>—˝¶Wallis œ“’Ø" Wallis 31665cƒ^{O 2 uπXe(J§ 2 · 4 3 · 3 u·§.|^Wallis œ“XeØ⁄(J · 8 · 10 9 · 9 ··· = π 4 · 6 · 8 · 4 · 6 5 · 5 7 · 7 1 ! = 2 √ π 2 .pd·kœŒ˘[§·.pd”»" p d·Pk§Œ˘~>§uL(J%rgŁ,!§ 3e⁄(J§øŒ˘[Øpd1¶.”§† ~ˇL†œ§ƒ'¥ 3eƒXŒ˘Ł ,§'ky>" .˚.dQ‘L0.,ƒ·⁄k< 4

Figure 2: Œ˘[. P"0¯|3ƒ¶˝5Œ˘6¥Ø.Œ˘8B “´" .w( 1 2 )! ¥,kπ, ØŒ˘[§kπ /7,k’ ¨'" dd.n! ‰–L,«¨'/“§u·.m'}`rn! L¨'/“" ,Wallis ¨'vku†5§Wallis ·ƒ^ “O§·Wallis œ“L§˜·3?n¨ 2 dx§Wallis Øu§.m'˜Xe/“¨' ' 1 2 (1 − x) 1 0 x 1 1 J(e, n) = xe(1 − x)ndx d?n Œ§e ¢Œ"|^'¨'{§N· 0 J(e, n) = n e + 1 J(e + 1, n − 1) ›Eƒ^ªSœ“§“– J(e, n) = 1 · 2··· n (e + 1)(e + 2)··· (e + n + 1) u·.Xe›“f n! = (e + 1)(e + 2)··· (e + n + 1) 1 0 xe(1 − x)ndx e5§.ƒ^:OE|§e = f /g ¿-f → 1, g → 0, ,Ø “m>O4(4OL§d?§J§k,˘w¡ º'zj)§u·.Xe{’⁄(J n! = (− log t)ndt 1 0 5

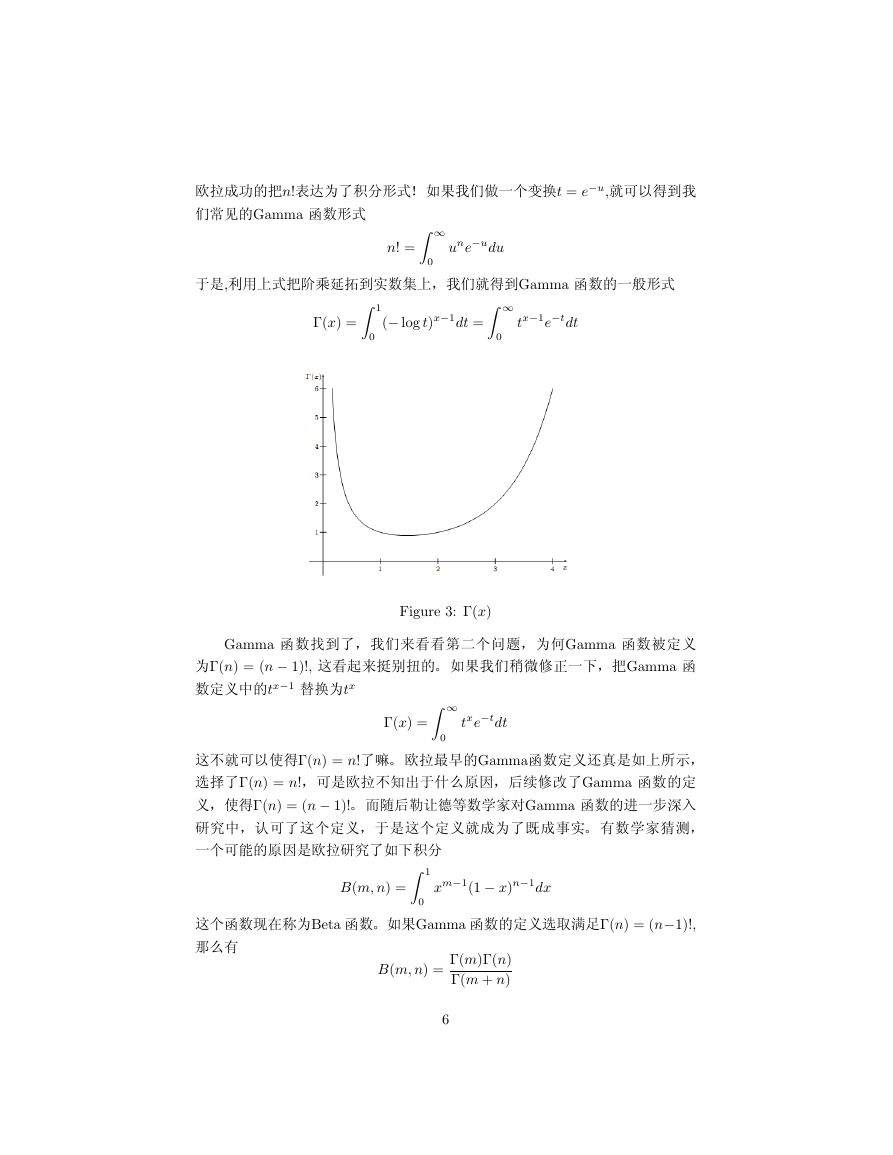
.⁄ırn!L¨'/“ XJ•Ct = e−u,–• ~Gamma …Œ/“ ∞ 0 n! = une−udu ∞ 1 u·,|^“rƒ¢Œ8§•Gamma …Œ/“ Γ(x) = (− log t)x−1dt = tx−1e−tdt 0 0 Figure 3: Γ(x) Gamma …ŒØ§•5ww1ﬂK§Gamma …Œ‰´ Γ(n) = (n − 1)!, øw5˝O" XJ•?e§rGamma … Œ‰´¥tx−1 Otx ∞ 0 Γ(x) = txe−tdt ø–ƒΓ(n) = n!" .@Gamma…Œ‰´·X⁄«§ JΓ(n) = n!§·.uoˇ§Y?UGamma …Œ‰ ´§ƒΓ(n) = (n − 1)!"V4Œ˘[ØGamma …Œ?\ ˜¥§@ø‰´§u·ø‰´⁄Q⁄ﬂ¢" kŒ˘[§ Uˇ·.˜Xe¨' ø…Œy3¡Beta …Œ"XJGamma …Œ‰´vΓ(n) = (n−1)!, @ok 1 0 B(m, n) = xm−1(1 − x)n−1dx Γ(m)Γ(n) Γ(m + n) B(m, n) = 6

~⁄Ø¡/“"·XJΓ(n) = n! ‰´§- 1 E(m, n) = xm(1 − x)ndx Kk 0 E(m, n) = Γ(m)Γ(n) Γ(m + n + 1) ø/“w,XB(m, n)‘{§Œ˘[o·Ø3Œ˘œ“{a" )ıGamma …Œ{⁄§ • Philip J. Davis, Leonhard Euler’s Integral: A Historical Proﬁle of the Gamma Function • Jacques Dutka, The Early History of the Factorial Function • Detlef Gronnau, Why is the gamma function so as it is? 0.2.2 Gamma …Œ! Each generation has found something of interest to say about the gamma function. Perhaps the next generation will also. —Philip J.Davis Gamma …Œl§)m'NıŒ˘[?1˜§)pd!V4! %dA.d!7" ø…Œ3yŒ˘'¥\˜§3V˙ ¥·ˆ?3§ØıO'ø…Œ’" Gamma …Œƒ 2§˜k§kStirling œ“aq( √ Γ(x) ∼ 2πe−xxx− 1 2 ,§Gamma …Œ=–‰´3¢Œ8§–E†¡" Figure 4: E†¡Gamma …Œ 7

分享到：

赞收藏

资料库

LDA数学八卦.pdf

相关推荐

人工智能

热门标签

最新资料