第1页 / 共26页
第2页 / 共26页
第3页 / 共26页
第4页 / 共26页
第5页 / 共26页
第6页 / 共26页
第7页 / 共26页
第8页 / 共26页
最小二乘法曲线拟合以及Matlab实现.docx
最小二乘法曲线拟合以及Matlab实现
目录
最小二乘法直线线拟合原理
曲线线拟合
Matlab实现代码
运行结果:
拟合曲线结果：
系数矩阵answer：
Matlab自带函数——polyfit
最小二乘法曲线拟合以及 Matlab 实现
在实际工程中，我们常会遇到这种问题：已知一组点的横纵坐标，需要绘制出一
条尽可能逼近这些点的曲线（或直线），以进行进一步进行加工或者分析两个变
量之间的相互关系。而获取这个曲线方程的过程就是曲线拟合。
目录
最小二乘法直线拟合原理
曲线拟合
Matlab 实现代码
最小二乘法直线线拟合原理
首先，我们从曲线拟合的最简单情况——直线拟合来引入问题。如果待拟合点集近似排列在
一条直线上时，我们可以设直线 y=ax+b 为其拟合方程，系数 A=[a,b]为待求解项，已知：
用矩阵形式表达为： Y=X0A，其中：
要求解 A，可在方程两边同时左乘 X0 的逆矩阵，如果它是一个方阵且非奇异的话。
但是，一般情况下 X0 连方阵都不是，所以我们在此需要用 X0 构造一个方阵，即方程两边
同时左乘 X0 的转置矩阵，得到方程: XT0Y=XT0X0A.
此时，方程的系数矩阵 XT0X0 为方阵，所以两边同时左乘新系数矩阵 XT0X0 的逆矩阵，便
可求得系数向量 A ，即：(XT0X0)−1XT0Y=A。
方程 A=(XT0X0)−1XT0Y 右边各部分均已知，所以可直接求解得到拟合直线的方程系数
向量 A。
曲线线拟合
当样本点的分布不为直线时，我们可用多项式曲线拟合，即拟合曲线方程为 n 阶多项式
y=∑ni=0aixi=anxn+an−1xn−1+...+a1x+a0。
用矩阵形式表示为： Y=X0A，其中：
待求解项为系数向量 A=[an,an−1,...,a2,a1,a0]T。
曲线拟合方程 Y=X0A 的求解方法与上面直线的求解方法一样，也是在方程 Y=X0A 两边
同左乘 X0 的转置矩阵得到: XT0Y=XT0X0A，
再同时在新方程两边同时左乘 XT0X0 的逆矩阵，得到：(XT0X0)−1XT0Y=A
上式左边各部分均已知，所以可直接求解得拟合曲线方程的系数向量 A。
如果它是一个方阵且非奇异的话。
一、奇异矩阵
1、奇异矩阵是线性代数的概念，就是对应的行列式等于 0 的矩阵。
2、奇异矩阵的判断方法：首先，看这个矩阵是不是方阵（即行数和列数相等的
矩阵。若行数和列数不相等，那就谈不上奇异矩阵和非奇异矩阵）。 然后，再看
此方阵的行列式|A|是否等于 0，若等于 0，称矩阵 A 为奇异矩阵；若不等于 0，
称矩阵 A 为非奇异矩阵。 同时，由|A|≠0 可知矩阵 A 可逆，这样可以得出另外
一个重要结论:可逆矩阵就是非奇异矩阵，非奇异矩阵也是可逆矩阵。
二、非奇异矩阵
1、n 阶方阵 A 是非奇异方阵的充要条件是 A 可逆，即可逆方阵就是非奇异方
阵。
2、对一个 n 行 n 列的非零矩阵 A，如果存在一个矩阵 B 使 AB = BA =I（ I
是单位矩阵），则称 A 是可逆的，也称 A 为非奇异矩阵。
3、一个矩阵非奇异当且仅当它的行列式不为零。
4、一个矩阵非奇异当且仅当它代表的线性变换是个自同构。
5、一个矩阵半正定当且仅当它的每个特征值大于或等于零。
6、一个矩阵正定当且仅当它的每个特征值都大于零。
7、一个矩阵非奇异当且仅当它的秩为 n。
Matlab 实现代码
clear
clc
x=[2,4,5,6,6.8,7.5,9,12,13.3,15];
y=[-10,-6.9,-4.2,-2,0,2.1,3,5.2,6.4,4.5];
[~,k]=size(x);
for n=1:9
X0=zeros(n+1,k);
for k0=1:k
for n0=1:n+1
%构造矩阵 X0
X0(n0,k0)=x(k0)^(n+1-n0);
end
end
X=X0';
ANSS=(X'*X)\X'*y';
for i=1:n+1
%answer 矩阵存储每次求得的方程系数，按列存储
answer(i,n)=ANSS(i);
end
x0=0:0.01:17;
y0=ANSS(1)*x0.^n
for num=2:1:n+1
;%根据求得的系数初始化并构造多项式方程
y0=y0+ANSS(num)*x0.^(n+1-num);
end
subplot(3,3,n)
plot(x,y,'*')
hold on
plot(x0,y0)
end
suptitle('不同次数方程曲线拟合结果，从 1 到 9 阶')
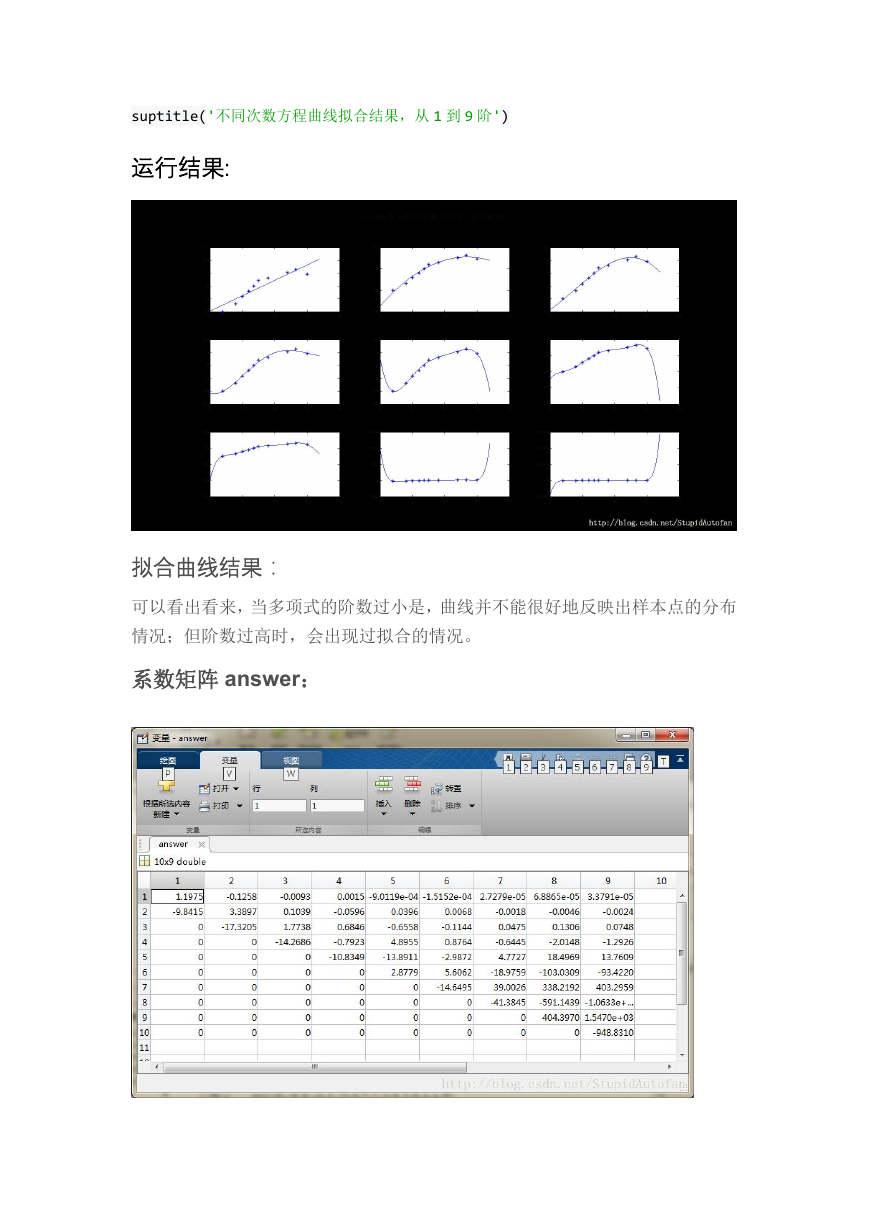
运行结果:
拟合曲线结果：
可以看出看来，当多项式的阶数过小是，曲线并不能很好地反映出样本点的分布
情况；但阶数过高时，会出现过拟合的情况。
系数矩阵 answer：
Matlab 自带函数——polyfit
在 matlab 中，也有现成的曲线拟合函数 polyfit，其也是基于最小二乘原理实现
的，具体用法为：ans=polyfit(x,y,n). 其中 x,y 为待拟合点的坐标向量，n 为多项
式的阶数。
下面代码是用 polyfit 函数来做曲线拟合：
clear
clc
x=[2,4,5,6,6.8,7.5,9,12,13.3,15];
[~,k]=size(x);
y=[-10,-6.9,-4.2,-2,0,2.1,3,5.2,6.4,4.5];
for n=1:9
ANSS=polyfit(x,y,n); %用 polyfit 拟合曲线
for i=1:n+1
%answer 矩阵存储每次求得的方程系数，按列存储
answer(i,n)=ANSS(i);
end
x0=0:0.01:17;
y0=ANSS(1)*x0.^n
for num=2:1:n+1
; %根据求得的系数初始化并构造多项式方程
y0=y0+ANSS(num)*x0.^(n+1-num);
end
subplot(3,3,n)
plot(x,y,'*')
hold on
plot(x0,y0)
end
suptitle('不同次数方程曲线拟合结果，从 1 到 9 阶')
运行结果：
用 polyfit 拟合的结果与第一份代码运行的结果基本一样
Matlab 的函数采样：
———————————————————————————————————————
clc;
clear all;
n = 20;
T = 2*pi;
step = T / n;
ii=1
t = (ii-1)*2*pi : step : 2*pi*ii;
y = sin(t);
figure(ii);
plot(t, y,'ro');
% tt{ii} = t;
%xx{ii} = t;
X2 = 0: step: 2*pi*ii;
Y2 = gaussmf(x2,[2 5]);
plot(x,y)
xlabel('gaussmf, P=[2 5]')
XX=x2+t;
YY=y2+y;
———————————————————————————————————————
%得到两个矩阵，保存 y 和 t 的值。
clear all;
n = 20;
T = 2*pi;
step = T / n; %步长
for ii=1:10 %取 1-10
t = (ii-1)*2*pi : step : 2*pi*ii;
y = sin(t);
end
———————————————————————————————————————
python 生成代码：
# 在 0-2*pi 的区间上生成 100 个点作为输入数据
X = np.linspace(0,2*np.pi,100,endpoint=True)
Y = np.sin(X)
# 对输入数据加入 gauss 噪声
# 定义 gauss 噪声的均值和方差
mu = 0
sigma = 0.12
for i in range(X.size):
X[i] += random.gauss(mu,sigma)
Y[i] += random.gauss(mu,sigma)
# 画出这些点
pt.plot(X,Y,linestyle='',marker='.')
pt.show()
———————————————————————————————————————
给图像加高斯噪声：
一般用于大一点的矩阵实验效果会更好，例如：
矩阵g 太小，所以不明显。
h=imread('photo.jpg');%读入彩色图片
c=rgb2gray(h);%把彩色图片转化成灰度图片，256 级
figure,imshow(c),title('原始图象');%显示原始图象
g=imnoise(c,'gaussian',0.1,0.002);%加入高斯噪声
figure,imshow(g),title('加入高斯噪声之后的图象');%显示加入高斯噪声之后
上面倒数第二句就是在原图加上高斯噪声的效果。
———————————————————————————————————————
x=(0:0.01:2);%采样频率 100Hz
y1=sin(2*pi*x);%产生频率 5Hz 的 sin 函数
plot(x,y1,'b');
z1=0.1*randn(1,201); %产生方差 N（0，0.12）高斯白噪声 （b=0.01/0.1/1） plot(x,z1,'b');
y2=y1+z1; %叠加高斯白噪声的正弦波
plot(x,y2,'b');
———————————————————————————————————————
目前代码：
clear all;
n = 2; %取样频率
T = 2*pi; %周期
step = (T / n)*0.1; %采样步长
t = (0 : step : 2*T);%取样 t 的函数值 采样频率
y = sin(pi/2*t); %取样 y 的值，产生频率 5Hz 的 sin 函数
figure(1);
plot(t,y,'b');
z1=0.3*randn(1,41); %产生方差 N（0，0.12）高斯白噪声 （b=0.01/0.1/1） plot(x,z1,'b');
y2=y+z1; %叠加高斯白噪声的正弦波
figure(2);
plot(t,y2,'ro');%展示加过噪声后的图像。
figure(3);
%其中 t 时自变量值，y2 是生成的采集点。
[~,k]=size(t);
for n=1:9
X0=zeros(n+1,k);
for k0=1:k
%构造矩阵 X0
for n0=1:n+1
X0(n0,k0)=t(k0)^(n+1-n0);
end
end
X=X0';
ANSS=(X'*X)\X'*y2';
for i=1:n+1
%answer 矩阵存储每次求得的方程系数，按列存储
answer(i,n)=ANSS(i);
end
x0=0 : step : 2*T;
y0=ANSS(1)*x0.^n
for num=2:1:n+1
;%根据求得的系数初始化并构造多项式方程
y0=y0+ANSS(num)*x0.^(n+1-num);
end
subplot(3,3,n)
plot(t,y2,'*')
hold on
plot(x0,y0)
end
clear all;
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
