第1页 / 共77页
第2页 / 共77页
第3页 / 共77页
第4页 / 共77页
第5页 / 共77页
第6页 / 共77页
第7页 / 共77页
第8页 / 共77页
PRML笔记-Notes on Pattern Recognition and Machine Learning.pdf
Checklist
Chapter 1 Introduction
Chapter 2 Probability Distribution
Chapter 3 Linear Models for Regression
Chapter 4 Linear Models for Classification
Chapter 5 Neural Networks
Chapter 6 Kernel methods
Chapter 7 Sparse Kernel Machine
Chapter 8 Graphical Models
Chapter 9 Mixture Models and EM
Chapter 10 Approximate Inference
Chapter 11 Sampling Method
Chapter 12 Continuous Latent Variables
Chapter 13 Sequential Data
Chapter 14 Combining Models
PRML 笔记
Notes on Pattern Recognition and Machine Learning (Bishop)
Version 1.0
Jian Xiao①
目录
Checklist
Chapter 1 Introduction
Chapter 2 Probability Distribution
..................................................................................................... 2
................................................................................ 4
............................................................ 10
.................................................. 14
Chapter 3 Linear Models for Regression
.............................................. 19
...................................................................... 26
........................................................................ 33
............................................................ 39
..................................................................... 47
.......................................................... 53
........................................................... 58
................................................................... 63
.................................................. 68
...................................................................... 72
................................................................. 74
Chapter 4 Linear Models for Classification
Chapter 5 Neural Networks
Chapter 6 Kernel methods
Chapter 7 Sparse Kernel Machine
Chapter 8 Graphical Models
Chapter 9 Mixture Models and EM
Chapter 10 Approximate Inference
Chapter 11 Sampling Method
Chapter 12 Continuous Latent Variables
Chapter 13 Sequential Data
Chapter 14 Combining Models
① iamxiaojian@gmail.com
Checklist
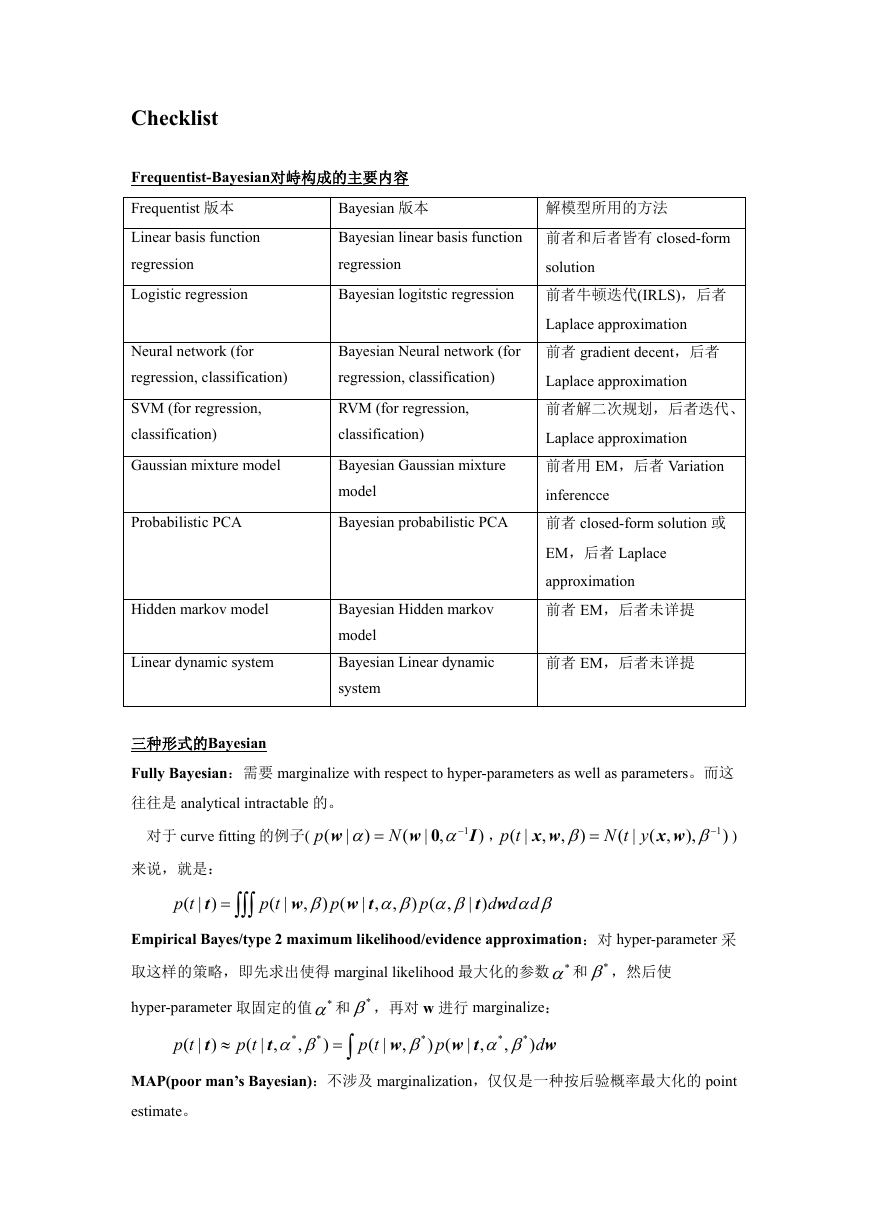
Frequentist-Bayesian对峙构成的主要内容
Frequentist 版本
Linear basis function
regression
Logistic regression
解模型所用的方法
Bayesian 版本
Bayesian linear basis function
regression
Bayesian logitstic regression 前者牛顿迭代(IRLS)，后者
前者和后者皆有 closed-form
solution
Neural network (for
regression, classification)
Bayesian Neural network (for
regression, classification)
SVM (for regression,
classification)
Gaussian mixture model
RVM (for regression,
classification)
Bayesian Gaussian mixture
model
Probabilistic PCA
Bayesian probabilistic PCA
Hidden markov model
Linear dynamic system
Bayesian Hidden markov
model
Bayesian Linear dynamic
system
Laplace approximation
前者 gradient decent，后者
Laplace approximation
前者解二次规划，后者迭代、
Laplace approximation
前者用 EM，后者 Variation
inferencce
前者 closed-form solution 或
EM，后者 Laplace
approximation
前者 EM，后者未详提
前者 EM，后者未详提
三种形式的Bayesian
Fully Bayesian：需要 marginalize with respect to hyper-parameters as well as parameters。而这
往往是 analytical intractable 的。
w
|
对于 curve fitting 的例子(
Nα
N t y
1
α−
0
,
x w
( ,
x w
,
p t
( |
1
β−
)
β
( |
w
p
(
I
)
，
)
=
(
|
,
=
),
)
)
来说，就是：
t
p t
( | )
= ∫∫∫
p t
( |
w
,
)
β
p
(
w t
|
,
αβ αβ
p
)
(
,
,
t w
| )
d d d
α β
Empirical Bayes/type 2 maximum likelihood/evidence approximation：对 hyper-parameter 采
取这样的策略，即先求出使得 marginal likelihood 最大化的参数 *α 和 *β ，然后使
hyper-parameter 取固定的值 *α 和 *β ，再对 w 进行 marginalize：
t
p t
( | )
≈
p t
( |
t
*
*
,
α β
,
)
= ∫
p t
( |
w
,
*
β
)
p
(
w t
|
*
*
,
α β
,
)
d
w
MAP(poor man’s Bayesian)：不涉及 marginalization，仅仅是一种按后验概率最大化的 point
estimate。
PRML 说的 Bayesian 主要还是指 Empirical Bayesian。
Optimization/approximation
Linear/Quadratic/Convex optimization：求线性/二次/凸函数的最值
Lagrange multiplier：带（等式或不等式）约束的最值
Gradient decent：求最值
Newton iteration：解方程
Laplace approximation：近似
Expectation Maximation (EM)：求最值/近似，latent variable model 中几乎无处不在
Variational inference：求泛函最值
Expectation Propagation (EP)：求泛函最值
MCMC/Gibbs sampling：采样
Latent variable model
Latent variable 连续
Probabilistic PCA/ICA/Factor Analysis
LDS
Latent variable 离散
GMM
Latent variable 独立
Latent variable 是 Markov chain HMM
Objective function/ Error function/Estimator
Likelihood：MLE 参数估计的 estimator，最常用的目标函数
Marginal likelihood：emprical Bayes/evidence approximation 中用于估计 hyper-parameter
Sum-of-square error：regression 常用
Posterior：MAP 参数估计
Negative log likelihood/cross-entropy：Logistic regression
Exponential error：Adaboost 的目标函数
Hinge error：SVM 的目标函数
Chapter 1 Introduction
1. Bayesian interpretation of probability
与其说是贝叶斯学派对“概率”这个概念的解释，不如说是概率碰巧可以作为量化贝叶斯学
派“degree of belief”这个概念的手段。
贝叶斯学派的出发点是“uncertainty”这个概念，对此给予“degree of belief”以表示不确定性。
Cox showed that if numerical values are used to represent degrees of belief, then a simple set of
axioms encoding common sense properties of such beliefs leads uniquely to a set of rules for
manipulating degrees of belief that are equivalent to the sum and product rules of probability.
因此之故，我们才可以 use the machinery of probability theory to describe the uncertainty in
model parameters.
2.
对parameter的观点，以及Bayesian对先验、后验概率的解释
对于 Frequentist 来说，model parameter w 是一个 fixed 的量，用“estimator”来估计；最常
见的 estimator 是 likelihood。
对 Bayesian 来说，w 本身是一个不确定量，其不确定性用 prior probability p(w)表示。
为了获知 fixed 的 w，Frequentist 进行重复多次的试验，获得不同的 data sets D；
对于 Bayesian 而言，there is only a single data set D, namely the one that is actually observed.
在得到一个 observation D 后，贝叶斯学派要调整原来对于 w 的 belief（prior probability），用
后验概率 P(w|D)表示调整后的 belief。调整的方法是贝叶斯定理。
Bayesian 的中心定理是贝叶斯定理，该定理 convert a prior probability into a posterior
probability by incorporating the evidence provided by the observed data。其中的条件概率 P(D|w)
表示的是，how probable the observed data set is for different settings of parameter vector w。
p w D
(
|
)
=
p D w p w
(
)
(
|
)
p D
(
)
=
∫
|
p D w p w
)
(
p D w p w dw
(
)
)
)
(
(
|
其中分母里的 p(D)只是用于归一化的量，使得 p(w|D)确实是一个概率。而 p(D)的计算已经
给出在上面的分母中。
（理解后验概率：即修正后的先验概率。例如，有C1,…,Ck 个类别，先验为P(C1)，…，
P(Ck)，这个时候如果给一个未知类别的数据让我们猜它是哪个类别，显然应该猜先验概率
最大的那个类别。在观察到数据x 后，计算后验概率P(C1|x)，…，P(Ck|x)；于是此时的“先
验”修正为 P’(C1)=P(C1|x)，…，P’(Ck)=P(Ck|x)。如果现在再来一个未知类别的数据让我
们猜，我们猜的方法仍旧是找先验概率最大的那个类别，只不过此时的先验概率是P’(C1)，…，
P’(Ck)。）
3. Bayesian和Frequentist的缺点
Bayesian 常受的批评之一：prior distribution is often selected on the basis of mathematical
convenience rather than as a reflection of any prior beliefs。 例如常选择 conjugate prior。
Frequentist 方法的缺点：Over-fitting problem can be understood as a general property of
maximum likelihood。
4. 应对over-fitting问题
Frequentist 控制 over-fitting 的方法：
1) regularization，即在目标函数中加入一个 penalty term。
L2 regularizer 被称为 ridge regression
L1 regularizer 被称为 Lasso regression
加入 penalty 的方法也叫 shrinkage method，因为它可以 reduce the value of the coefficients.
2) cross-validation，即留出一部分数据做 validation
Cross-validation 也是一种进行 model selection 的方法。利用留出来的 validation data，可以
选择多个所训练 model 中的最好的一个。
Bayesian 控制 over-fitting 的方法：Prior probability
5. Bayesian方法面临的主要问题：marginalization计算困难
Marginalization lies at the heart of Bayesian methods.
Bayesian methods 的应用长期受制于 marginalization。对于一个 full Bayesian procedure 来
说，要 make prediction 或 compare different models，必要的一步是 marginalize (sum or integrate)
over the whole of parameter space.
两方面发展起来的方法克服了做 marginalization 的困难：
第一种是 sampling，例如 Markov chain Monte Carlo。Monte Carlo method 的优点是 flexible
而广泛用于各种 model 中；缺点是 computationally intensive，主要用于 small-scale problems.
第二种是 deterministic approximation，例如 variational Bayes 和 expectation propagation，优
点是可用于 large-scale applications.
6.
Curve fitting为例子演示三种方法
1) MLE，直接对 likelihood function 求最大值，得到参数 w。该方法属于 point estimation。
2) MAP (poor man’s bayes)，引入 prior probability，对 posterior probability 求最大值，得到
w。MAP 此时相当于在 MLE 的目标函数（likelihood function）中加入一个 L2 penalty。该方
法仍属于 point estimation。
3) fully Bayesian approach，需要使用 sum rule 和 product rule（因为“degree of belief”的
machinery 和概率相同，因此这两个 rule 对 “degree of belief”成立），而要获得 predictive
distribution 又需要 marginalize (sum or integrate) over the whole of parameter space w。
p t
( |
x X t
,
, )
x w
,
)
p
(
w X t w
, )
d
|
= ∫
p t
( |
其中，x 是待预测的点，X 是观察到的数据集，t 是数据集中每个数据点相应的 label。
其实是用参数 w 的后验概率为权，对 probability 进行一次加权平均；因此这个过程需要
对 w 进行积分，即 marginalization。
7. PRML所需要的三论：Probability theory, decision theory and information theory
8. 两个阶段：inference与decision
整个问题的 solution 分为两阶段：先做 inference，然后做 decision。在 inference stage，要
得到联合概率分布或者后验概率分布；在 decision stage，则用 posterior probability to make
optimal class assignments。
9.
三种解决decision problem的不同方式
1) discriminant function: map inputs x directly into decisions. 因此 discriminant function 把
inference 和 decision 合作一部解决了。
2) discriminant model: 第一步，解决 inference problem，determining the posterior class
probabilities,
kP C x
(
|
)
；第二步，解决 decision problem，对于新给定的 x，把它分配给某一
个 class。
3) generative model：explicitly or implicitly model the distribution of inputs as well as outputs.
第一步，得到 class-conditional density
P
(
Cx
|
)k
或者 joint distribution
P
Cx
( ,
)k
；第二步，
在前一步的基础上得出 posterior；第三步，decision problem。
10.
评述三种解决决策问题方式的缺点
Generative model 的缺点：如果只是 make classification decision，计算 joint distribution 是
wasteful of computational resources and excessively demanding of data。一般有后验概率就足够
了。
Discriminant function 的缺点：该方法不求后验概率，然而 there are powerful reasons for
wanting to compute the posterior probabilities：
(1) 当 loss matrix 可能随时间改变时（例如 financial application），如果计算出来后验概率，
那么解决 decision problem 只需要修改 expected loss 目标函数；没有后验概率的 discriminant
function 只能全部重新学习。
(2) 当正负样本不平衡时（例如 X-ray 图诊断癌症，99.9%可能都是无癌症样本；又如垃
effects of the modification to the training data，即把 (
balanced data set 用于训练；训练得到一个后验概率 (
圾邮件的情况，绝大多数邮件都不是垃圾邮件），为了获得好的分类器，需要人工做出一个
kP C x 后，需要 compensate for the
kP C x 除以 balanced data set 的先验
kP C x 。没有
)kP C ，再乘以真实数据的先验 (
(
后验概率的 discriminant function 是无法用以上方法应对正负样本不平衡问题的。
)kP C ，从而得到了真实数据的后验概率 (
)
)
)
|
|
|
(3) Combining models（模型融合）：对于复杂应用，一个问题可能分解成多个子问题，例
如疾病诊断，可能除了 X-ray 图片数据 Ix ，还有血液检查数据 Bx 。与其把这些 heterogeneous
information 合在一起作为 input，更有效的方法是 build one system to interpret the X-ray images
and a different one to interpret the blood data。即有:
P C x x
(
,
|
k
I
)
∝
B
∝
P x x C P C
(
(
)
,
|
B
k
I
)
k
P x C P x C P C
(
)
(
)
(
|
|
B
k
I
k
)
∝
k
P C x P C x
(
|
|
k
k
)
I
P C
(
(
)
k
)
B
其中假设了 Ix 和 Bx 关于类别 kC 条件独立。
11.
Criteria for making decisions
1) Minimizing the misclassification rate
2) minimizing the expected loss：两类错误的后果可能是不同的，例如“把癌症诊断为无癌
症”的后果比“把无癌症诊断为癌症”的后果更严重，又如“把正常邮件诊断为垃圾邮件”的后
果比“把垃圾邮件诊断为正常邮件”的后果更严重；这时候，少犯前一错误比少犯后一错误更
有意义。为此需要 loss function 对不同的错误的代价做量化。设集合 A={a1,...,ap}是所有可
能的决策，决策函α：χ→A把每个观察数据x ϵ χ映射到一个决策α(x)，那么有
arg min (
R a x
x
( )
α
=
)
|
i
其中 (
iR a x 表示的条件风险：
)
|
R a x
(
|
i
)
c
= ∑
j
1
=
λ ω ω
j
a
i
P
(
)
(
|
j
|
x
)
i
j
|
)
aλ ω 是对于特定的真实类别是 jω 的数据，决策为 ia 时的 loss 或 risk，即表示
(
a xλ
(
xω 是当观察到 x 后，类别 jω 的后验概率。
ω∈ ； (
jP
)
)
|
|
j
i
决策函数α(x)总是把观察数据映射到条件风险最小的决策上。
于是，决策函数α(x)的总的 risk 是：
a A
∈
i
R
[
]
α
α= ∫
(
R
x
( ) |
x p x dx
) ( )
)
x
xα
( ) |
在所有可能观察数据（特征空间）分布下的期望值。
R
即条件风险 (
12. 熵
Entropy is a lower bound on the number of bits needed to transmit the state of a random
variable.
某随机变量 X，x 为其一个取值，概率为 p(x)，则
1) 该值的编码长度是
2)该随机变量的熵：
2
log
( )p x
−
∫
- p(x)log p(x)dx
2
，为平均编码长度
以上以 2 为低，单位是“比特”；如果以自然对数 e 为地，则是“奈特”。
13.
条件熵，相对熵，互信息
Conditional entropy：设有 joint distribution p(X,Y)，则条件熵 H[Y|X]为一个期望/平均值：
H Y X
[
|
]
|
=
∫
(
= −∫∫
(
)
=
=
H Y X x p X x d x
p y x dxdy
)log (
p x y
( ,
)
)
|
根据上面的定义，可见要定义条件熵 H[Y|X]，先需定义当给定 X=x 时，Y 的熵。即：
H(Y | X = x) = - p(y | x)logp(y | x)dy
∫
Relative entropy：设有一个未知的分布 p(x)，而 q(x)为我们所获得的一个对 p(x)的近似；
按照 q(x) (而非真实分布 p(x))对该随机变量的各个值进行编码，平均编码长度比用真实分布
p(x)进行编码要额外长多少？答案是相对熵(KL 距离)KL(p||q)。即
∫
(- p(x)lnq(x)dx) - (- p(x)lnp(x)dx) = - p(x)ln{
∫
∫
q(x)
p(x)
}dx
注意第一项，由于按照 q(x)来对随机变量的值编码，因此 q(x)在对数里面；而实际的分布是
p(x)，因此实际的平均长度是按照 p(x)计算的，p(x)在外面。
Mutual information：如果两个随即变量 X,Y 是独立的，那么有 p(x, y)=P(x)P(y)；当二者并
不独立时，我们希望可以度量它们离独立还有多远，这个度量就是互信息：
I[x, y] = KL (p(x, y) || p(x) p(y)) = H[x] – H[x|y] = H[y] – H[y|x]
对互信息的另一个解释是：当观察到 x（或 y）后，y（或 x）的 uncertainty 的减少量。
注意到-lnx 是凸函数，利用凸函数的 Jensen’s inequality，易证明 KL 距离非负，且
KL(p(x)|q(x)) = 0 当且仅当 p(x) = q(x)对每个 x 成立（因为-lnx 是严格凸的）。
14. 习题 1.14
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
