信息论与编码第六章课后习题答案.pdf-资料库

第六章课后习题【6.1】设有一离散信道，其信道传递矩阵为 1 2 1 6 1 3 1 3 1 2 1 6 1 6 1 3 1 2 并设 =xP ( 1 ) 1 2 ， xP ( ) 2 = xP ( ) 3 = 1 4 ，试分别按最小错误概率准则与最大似然译码准则确定译码规则，并计算相应的平均错误概率。解：假设输入符号集和输出符号集分别为按照最大似然译码规则，选择如下： xxx ,{ 1 }, 3 2 和 yy ,{ 1 2 , y 3 } 。 yF ( 1 yF ( 2 yF ( 3 ) ) ) = = = 平均错误概率为： x 1 x x 2 3 ) yPxP ( ( y + + j i 1 2 1 3 * 对应的 xY 1 + 3 1 6 | x i ) j 1 6 P E = = = X 1 2 1 2 如果需要按照最小错误概率译码，需要首先求出其联合概率矩阵： 1 4 1 24 1 12 1 6 1 8 1 24 1 12 1 12 1 8 œ œ œ œ œ œ ß ø Œ Œ Œ Œ Œ Œ º Ø ł Ł ł Ł - œ œ œ œ œ œ ß ø Œ Œ Œ Œ Œ Œ º Ø

最小错误概率译码规则应如下：此时错误概率为： yF ( 1 yF ( yF ( 2 3 = = = ) ) ) x 1 x 1 x 3 j j i i ) ) yPxP ( ( y yxP ( , y 1 8 1 12 + ++ j | x i ) j + 1 12 1 24 xY * 对应的 + 1 24 X xY * 对应的 P E = = = = X 1 12 11 24 【6.2】计算码长 5=n 的二元重复码的译码错误概率。假设无记忆二元对称信道中正确传递概率为 p ，错误传递概率为 p -=1 。此码能检测出多少错误？又能 p 纠正多少错误。若 01.0=p ，译码错误概率是多大？解：将 0 和 1 编成 00000 和 11111 后，当传输过程中产生 1 位至 4 位错误时均可检测出，但产生 5 位错误却无法检测出，同时，如果输入等概率分布，当传输过程中存在 1 位错误以及 2 位错误时，可以自动纠正。此时的错误概率为：错 3 位的概率为： ppC 3 3 5 2 ；错 4 位的概率为： ppC 4 4 5 ； 5 pC 错 5 位的概率为： 5 5 因此，译码错误概率为： ppC 3 3 5 2 + 4 5 pCppC 4 + 5 = .1 02961 10 5 5 5 【6.3】设某二元码为 {=C 11100 01001 , 10010 , , 00111 } （1）计算此码的最小距离 mind ；（2）计算此码的码率 R ，假设码字等概率分布； - - - ·

（3）采用最小距离译码准则，试问接收序列 10000，01100 和 00100 应译成什么码字？（4）此码能纠正几位码元的错误？解：（1）此码字的最小距离（2）此码字的码率 R = = d min M log n 3 = ； 2 5 比特/码符号；（3）采用最小距离译码，10000 应译成 10010；01100 应译成 11100；00100 译成 11100、00111 均可；（4）由于 d min ·== + 1123 ，因此此码能纠正 1 位码元的错误。【 6.4 】设无记忆二元对称信道的正确传递概率为 p , 错误传递概率为 p -=1 << p p 。令长度为 n 的 M 个二元码字 =a i ( aa L i 1 i 2 a ni ) kia ，其中 }1,0{˛ （码字为等概率分布），接收的二元序列为 =b j ( bb L j 1 j 2 b nj ) ， kjb }1,0{˛ 。试证明：采用最小距离译码准则可使平均译码错误概率 EP 达到最小，并且 P E -= 1 1 M i D * p j p Dn * j 证明：构造函数 =)( xf x pp xn ，有 xf )( = pp x xn ln p pp x xn ln p < 0 因此该函数为减函数，即当 D £ * j D ij 时，有 p D * j p Dn * j D pp ij n Dij 。因此按照最小距离选择的译码规则 b =jF ) ( * a ，使 D £ * j D ij 成立，必然会有 D * j p p Dn * j D pp ij n Dij ，即 E P P E 其中 EP 为最小距离译码得到的正确概率，而 EP¢ 则是其他译码得到的正确概率， - - - ¢ - - - - ‡ - - ‡ ¢ ‡

进一步可以得到运用最小距离译码得到的错误概率为最小。【6.5】对于离散无记忆强对称信道，信道矩阵为： = P 1 r p 1 p M p r 1 1 p p M p r r 1 1 p p M p r 1 r 1 r 1 L L r r p p M 1 1 L 1 p 试证明对于此信道，最小距离译码准则等价于最大似然译码准则。证明：当信道发送符号序列为 =a i ( aa L i 1 i 2 ) a ni ，接收符号序列为 =b j 时，信道矩阵中的条件概率为： ( bb L j 1 j 2 ) b nj P ( ab | j ) i = = = j 1 ( bbP ( bP j 1 p | r 1 j 2 n j L b ) ( bPa i 1 D ( , ) ba i j | aa i 1 i 2 L a i n ) ) L ) Dn | a i 2 p j 2 ( 1 ( bP | a i n j n ) ( , ba i j ) 按照最大似然译码规则，选择 b =jF ) ( * a ，使 P ( ab | j > * ) P ( ab | j ) i 成立，即 D * , ba ( ) j ( 1 ) Dn p * , ( ba ) j > p r 1 D ( , ba i j ) ( 1 ) Dn p ( , ba i j ) p r 1 因此有 D * , ba ( ) j D ( , ba i j ) ( -> 1 ) D p * ( , ba ) j D ( , ba i j ) p r 1 一般情况下， p -= 1 > p 1 2 ，因此有 D 小距离译码规则。 * ( ba , ) j D ( ba , i ) 成立，而这即为最 j 【6.6】某一信道，其输入 X 的符号集为 1,0{ 2 }1, ，输出Y 的符号集为 }1,0{ ，信道矩阵为 œ œ œ œ œ œ œ œ ß ø Œ Œ Œ Œ Œ Œ Œ Œ º Ø - - - - - - - - - - - - - - ł Ł - - - - ł Ł - - ł Ł - - - ł Ł - £

= P 1 1 2 0 0 1 2 1 现有四个消息的信源通过这信道传输（消息等概率出现）。若对信源进行编码，我们选这样一种码 C {(: 1 xx , 2 1, 2 1, 2 )} ， 10或˛ix （ 2,1=i ）其码长为 4=n ，并选取这样的译码规则 1, 2 （1）这样编码后信道的信息传输率等于多少？ yyf , ( yy , 3 1, 2 = ) ( yy , 1 2 4 , 2 1 ) （2）证明在选用的译码规则下，对所有码字 0=EP 。解：输入码字不同的个数共有 4 个，因此编码后信道的信息传输率为比特/码符号 1 2 =R 100 1 2 2 1/4 1/4 1/4 1/4 0 0 0 0 0 0 0 0 0 0 0 0 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 4 1 log = 2 4 101 2 0 0 0 0 1/4 1/4 1/4 1/4 0 0 0 0 0 0 0 0 1 2 110 2 0 0 0 0 0 0 0 0 1/4 1/4 1/4 1/4 0 0 0 0 1 2 111 2 0 0 0 0 0 0 0 0 0 0 0 0 1/4 1/4 1/4 1/4 œ œ œ œ œ œ ß ø Œ Œ Œ Œ Œ Œ º Ø

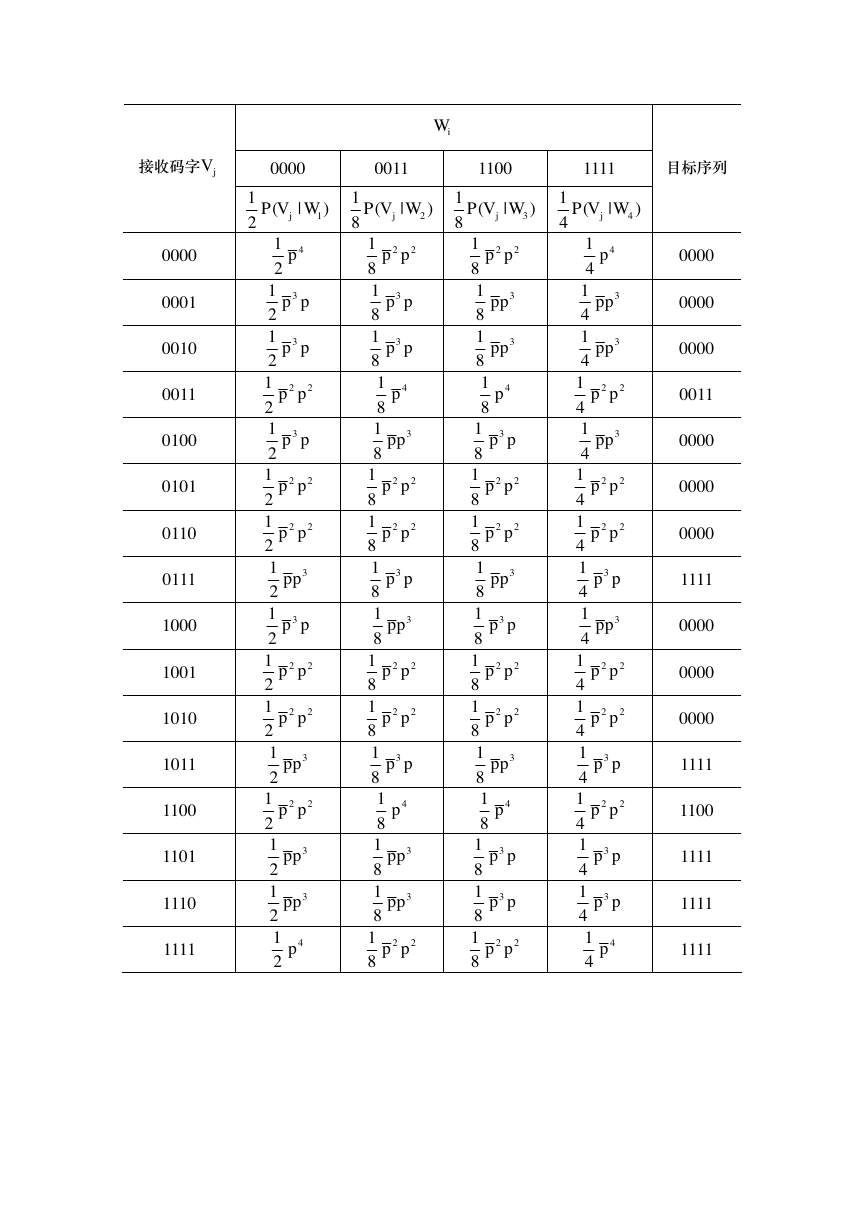
可以看出，通过上述译码，对每一个输出都有一个输入与其对应，通过计算，可得其平均错误概率 0=EP 。【6.7】考虑一个码长为 4 的二元码，其码字为 =W 1 0000 =W ， 2 0011 ， 1100 =W 3 ， =W 4 1111 。假设码字送入一个二元对称信道（其单符号错误概率为 p ，且 01.0

接收码字 jV 0000 0011 1100 1111 目标序列 iW 3 2 2 2 4 pp 3 pp 3 pp 2 pp 2 1WVP j ( | 1 p 2 1 pp 3 2 1 2 1 2 1 2 1 2 1 pp 2 2 1 pp 2 1 2 1 2 1 pp 2 2 1 pp 2 1 pp 2 2 1 pp 2 1 pp 2 1 p 2 pp 2 pp 3 2 2 4 2 3 3 3 ) 1 8 2 2 3 4 2 | pp3 pp 2 pp 2 pp 2 2WVP j ( 1 8 1 8 1 pp3 8 1 p 8 1 pp 8 1 8 1 8 1 pp3 8 1 pp 8 1 8 1 8 1 pp3 8 1 p 8 1 pp 8 1 pp 8 1 8 pp 2 pp 2 pp 2 3 2 2 4 3 3 2 ) 1 8 3 2 2 4 3 3 2 | pp 2 3WVP j ( 1 pp 2 8 1 pp 8 1 pp 8 1 p 8 1 pp3 8 1 8 1 pp 2 8 1 pp 8 1 8 1 8 1 pp 2 8 1 pp 8 1 p 8 1 8 1 8 1 8 pp 2 pp 2 pp3 pp3 pp3 2 2 3 4 2 ) 1 4 2 2 3 2 3 3 4 pp 2 pp 2 4WVP j ( | 1 p 4 1 pp 4 1 pp 4 1 pp 2 4 1 pp 4 1 4 1 4 1 pp3 4 1 pp 4 1 4 1 4 1 4 1 4 1 4 1 pp3 4 1 p 4 pp 2 pp 2 pp 2 pp3 pp3 3 2 2 2 4 ) 0000 0000 0000 0011 0000 0000 0000 1111 0000 0000 0000 1111 1100 1111 1111 1111 1 2 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

【6.8】设一种离散无记忆信道，其信道矩阵为 = P 1 2 1 2 0 0 0 1 2 0 0 0 1 2 0 1 2 1 2 0 0 0 0 1 2 1 2 0 0 0 0 1 2 1 2 （1）计算信道容量C ；（2）找出一个码长为 2 的重复码，其信息传输率为 1 2 log 5 （即 5 个码字）。如果按最大似然译码准则设计译码器，求译码器输出端的平均错误概率 EP （输入码字等概率）。（3）有无可能存在一个码长为 2 的码，使 )( =i eP （ 0 5,4,3,2,1=i ），即 0=EP ，如存在的话请找出来。解：（1）观察该信道，其每一行数据都是第一行数据的置换，每一列数据都是第一列数据的置换，因此该信道是对称信道，其信道容量为： = C log Hr 1( 2 1, 2 )0,0,0, = log 322.115 = 比特/码符号（2）假设信道中的输入符号集和输出符号集为{0,1,2,3,4}，进行二次重复码，编得 00、11、22、33、44 其码率为 SHR )( = n = 1 2 log 5 比特/码符号。此时，输出方可能有 25 种可能性，进行最大似然译码，如下表所示。错误概率为 œ œ œ œ œ œ œ œ œ œ œ ß ø Œ Œ Œ Œ Œ Œ Œ Œ Œ Œ Œ º Ø - -

资料库

信息论与编码第六章课后习题答案.pdf

相关推荐

课程资源

热门标签

最新资料