logo资料库

基于双种群遗传算法的公交线路发车间隔优化 (2012年).pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.38M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    ###E###
    560 深圳大学学报理工版 t; = C~ L (ωl，k~k+lll，k~k+l Vl ，k~k+l ) 第 29 卷 (3) 传算法优化发车间隔和松弛时间.杨兆升 [5 J 提出了 以社会效益最大化为目标的发车频率优化模型.宋 端等 [6] 运用机会约束规划方法，研究随机需求条件 下公交运营设计的优化问题.于滨等 [7] 针对整个公 交系统，以运营总成本最低为目标建立了一个双层 的公交线路发车频率优化模型. 通常一个城市公交系统中公交车辆的规模是确 定的.因此，在设计发车间隔时，若忽略公交车辆 规模的限制，则会影响研究结果在实际中应用.本 研究在车队总规模固定的前提下，以乘客和运营者 总费用最小为目标，建立了一个模型以优化公交线 路的发车间隔.当城市规模较大、公交线路较多 时，该模型较复杂，使用解析算法很难在可接受的 时间内求得结果.遗传算法 (genetic algorithm , GA) 是近年发展起来的一种进化算法，巳成功用 于很多领域 [8-9] 本研究采用遗传算法对该模型进 行求解，并通过双种群提高算法的求解性能 [ω 1 发车问隔优化模型 运营者和乘客是公交系统中两个相互权衡的因 素.在乘客数量不变时，运营者希望发车间隔尽可 能大，以减少其可变成本，而发车间隔变大，会增 加乘客的候车时间，无疑增加了乘客的时间费用. 只有同时考虑运营者和乘客双方利益，才能使城市 公交系统获得最大的社会效益.本研究分别建立乘 客总费用函数和运营者总费用函数，并在此基础上 构建公交发车间隔优化模型. 1.1 乘客时间费用函数 其中， tpllssen 为乘客时间费用;可和 c; 分别表示乘客 等车时间费用系数和乘车时间费用系数 Ul. k 为公 交线路 J 第 k 站等待的乘客数;可为乘客等待公交线 路 l 的期望时间，本研究设乘客到达服从均匀分布， 则可 = h/2; ψ 为惩罚系数，与乘客错过的车辆数 目成正相关，反映了由于车辆容量不足时无法上车 的乘客的额外费用，可以用大于 1 的整数或用发车 频率乘以等待的车辆数表示;岛 k 为公交线路 l 第 k 站上因无法乘车而滞留的乘客数，即 δl ，k→k+l 屿 ， k - bi.k; hl 为公交线路 l 的发车间隔，该变量是模型 的决策变量 ;ωi.k→k+l 为公交线路 l 第 k 站到第 k + 1 站区间上公交车内乘客的舒适系数，本研究采用拥 挤度来表示，即 ωl. k~k+l 二 Vi.k~k+l h / (HV); H 为优 化周期 V 为标准车辆的额定容量 Vm因为车辆的最 大载客数量 ll. k~k+l 为公交线路 1 第 k 站到第 k + 1 站 的平均运行时间 Vl.k~k+l 为公交线路 J 第 k 站到第 k V l. k k+l + bi.k - + 1 站间车内的乘客数，即 Vl.k~k+l αi.k; αi.k 为公交线路 l 第 k 站下车的乘客数， αl.k V l.k -l-.k X qu; qi.k 为公交线路 1 第 k 站乘客下车比率， 即该站点优化周期内的下车人数占从该站点到终点 所有站点下车人数的比例 bu 为公交线路 l 第 k 站 上车的乘客数，即 b" = [Ul ，k ， 屿，k 运 IH/hl 丁 x (凡JaX l , k - 11 H/hl 丁 x (Vmax - V l. k - l - V l .k- 1 k + αl ，k) k + αi.k) , otherwise (4) 1. 2 运营者费用函数 运营者费用主要包括燃油消耗、车辆折旧、维 与运营调度相关的乘客时间费用( tpassen )主要 修、司机及售票员的工资等，其表达式为 由乘客等车和乘车两部分费用构成.其中，等车时 间费用 (tn 通常分为两种情况:①乘客到站后， 等待第 1 辆公交车的时间费用，通常用乘客数与平 均期望等车时间的乘积表示;②乘客到站后，未 能乘坐第 1 辆到站的公交车，必须等待下一辆车的 等待时间费用.乘车时间费用 (t; ) 主要指乘客在车 内所耗费的时间费用，包括乘客客观耗费时间和车 内拥挤程度所造成的主观时间费用.乘客时间费用 函数的具体形式为 t阿en = L (t;' + t;) t;' c; 二 (μl，kt~ + ψδl，khl) (1) (2) (5) 1阳 = L 盯 盯= C~I H/hll + C: 三 IH/hl 丁 x tl ,k (6) 其中 Toper表示运营者费用;打表示公交线路 l 的运 营费用 ;c; 和 C; 分别表示公交车辆的费用系数和公 交公司的运营费用系数. 1. 3 公交发车间隔优化模型 k+l 要使整个城市公交系统的总费用最低，必须找 到乘客总时间费用和运营者费用之间的均衡点，本 研究采用线性加权法将两种费用转化成单目标优化 问题，得到公交发车间隔优化模型为 W passen t passen + W oper Toper min Ttotal (7)
    第 6 期 姚锦宝，等:基于双种群遗传算法的公交线路发车间隔优化 561 s. t. hl ~ 60 L， gl 运 G (8) (9) 通过一系列 (0 ， 3600J 的随机数组成.由于模型存 在车队规模的约束，因此在产生初始染色体时，如 W passen' W op巳r 二"， 0 W passell + W op{~r = 1 (1 0) ( 11 ) 其中， T，o，a' 为系统总成本 Wpassen 和 Woper 分别为乘客 时间费用和运营着费用的权重值 ; gl 为线路 l 公交车 辆的规模，即 gl = 12 L, t l ,k--'k+l/hl l , Il 表示向下 取整，如 16. 5l = 6; G 表示公交网络的车辆总数. 1. 4 权重确定 测试前，需要确定优化模型目标函数中乘客时 间费用和运营者费用的权重值 Wpassen 和 Woper " 本研究 以大连市公交系统所有公交线路的乘客时间费用和 运营者费用的比例作为两个权重的取值， lz() 果不满足车队规模约束，即 L， gl > G ， 则重新生成 染色体，直至产生一个种群. 2.2 适应值函数 标准遗传算法适宜求解目标最大的优化模型， 本研究通过引人一个常数 Q ， 将目标函数 (7) 转换 为最大化函数.此外，遗传算法在进化过程中可能 会产生一些违背模型约束的染色体.通常有 2 种方 法解决这个问题，一种是通过给该染色体增加一个 惩罚因子，来降低其在后续进化中存活的几率，但 是并不强制扔掉该染色体;另一种则是修改不满足 约束的染色体的基因片段，以使其满足约束.本研 究采用第 1 种方法对目标函数进行处理，得到遗传 算法适应值函数为 三( t p…(i) + 凡川 i)) (1 2) F = Q/[T+ φ(7) ( L, g/ -的] w叩 1 - Wpassen 其中， tpassen (i) 和 Toper ( i) 分别表示第 i 条线路乘客 时间费用和运营者费用.假设有 2 条公交线路，它 们的乘客和运营费用分别为 (0.9 ， 0.76) 和 (0.8 ， 0.78) ，则有 ω阳ssen = (0.9 + O. 8)/(0. 9 + 0.76 + O. 8 + O. 78) = O. 52 , w叩盯 = 1 - w阳osen O. 48. 2 双种群遗传算法 遗传算法 (GA) 是模仿自然选择、物种进化 和群体遗传学建立的一种随机搜索技术，已被成功 用于工业、经济管理、交通运输及工业设计等领 域 [11] 标准遗传算法在进化过程中，由于生成的 染色体可能重复或相似，在种群规模较小时容易发 生早熟[山3] 与传统遗传算法不同的是，双种群遗 传算法在优化前，同时生成 2 个种群， 2 个种群的 编码和规模完全相同. 2 个种群独立进行进化操作 (交叉和变异) .在进行选择操作时，双种群遗传算 法采用"混合选择"方式，在进化过程中可以保持 种群相对丰富多样，减小早熟导致收敛的可能，提 高求解质量. 2. 1 编码策略 公交发车间隔优化模型网络中每条线路的发车 间隔(秒)为决策变量，本研究采用整数编码的方 案，编码为 1 e l , e 2 , …, e l , … , e N 1. 初始种群是 (1 3 ) (1 4 ) φ(7) = f ‘ rß， 7β) ，g-， > G l~. l 0 . otherwise 其中 ， F 表示适应值函数 ;Q 、 βl 和 β2 是常量， βl 和 β2 用来控制对违反约束染色体的惩罚强度. 2.3 选择操作 双种群遗传算法与标准遗传算法最大区别在于 染色体的选择.双种遗传算法中染色体选择步骤 为:首先，将 2 个种群的所有染色体合并，形成一 个 2 倍于原种群规模的染色体集合;然后，分别从 这个染色体集合中选择各自的新种群.在选择过程 中，为避免新种群中包含重复的染色体，禁止同一 条染色体出现在同一种群中.本研究选用了精英策 略，将适应值最高的染色体复制到下一代，确保最 好的基因在下一代进化中不会丢失，避免退化. 2.4 交叉操作 交叉操作是通过交换两个父染色体的基因来产 生后代.具体交叉操作为 (;「 δyarenl ， j + (1δ) eyurent , L l efIld ， 2= 「 δ ， leyarenl , 2 + (1 _δ 'l)erare时 ， ll , 币"，
    深圳大学学报理工版 第 29 卷 辆的额定容量、最大载客量、乘客的等车、乘车时 间费用系数、公交车辆的费用系数和公交公司的运 营费用系数等数据.根据这些实际数据，对 Wpa 和切0叩阳P严阳巳盯r 2 个目标的权重进行标定.最终模型和算法 中相关参数的设定如表 1 和表 2. 表 1 优化模型的参数取值 Table 1 Parameters in headway optimization model H 3600 s 4 V 80 4 Vmux 120 C~ 2.0元/小时 8.75方车 3 元Y分 'p 2 Wpassen 0.53 CW P 2. 7 元/小时 W oper 0.47 表 2 双种群遗传算法中的参数取值 Table 2 Parameters in DGA Q 1 000 λ 3 Psiz‘祖 240 R p ,- 0.6 Pm o. 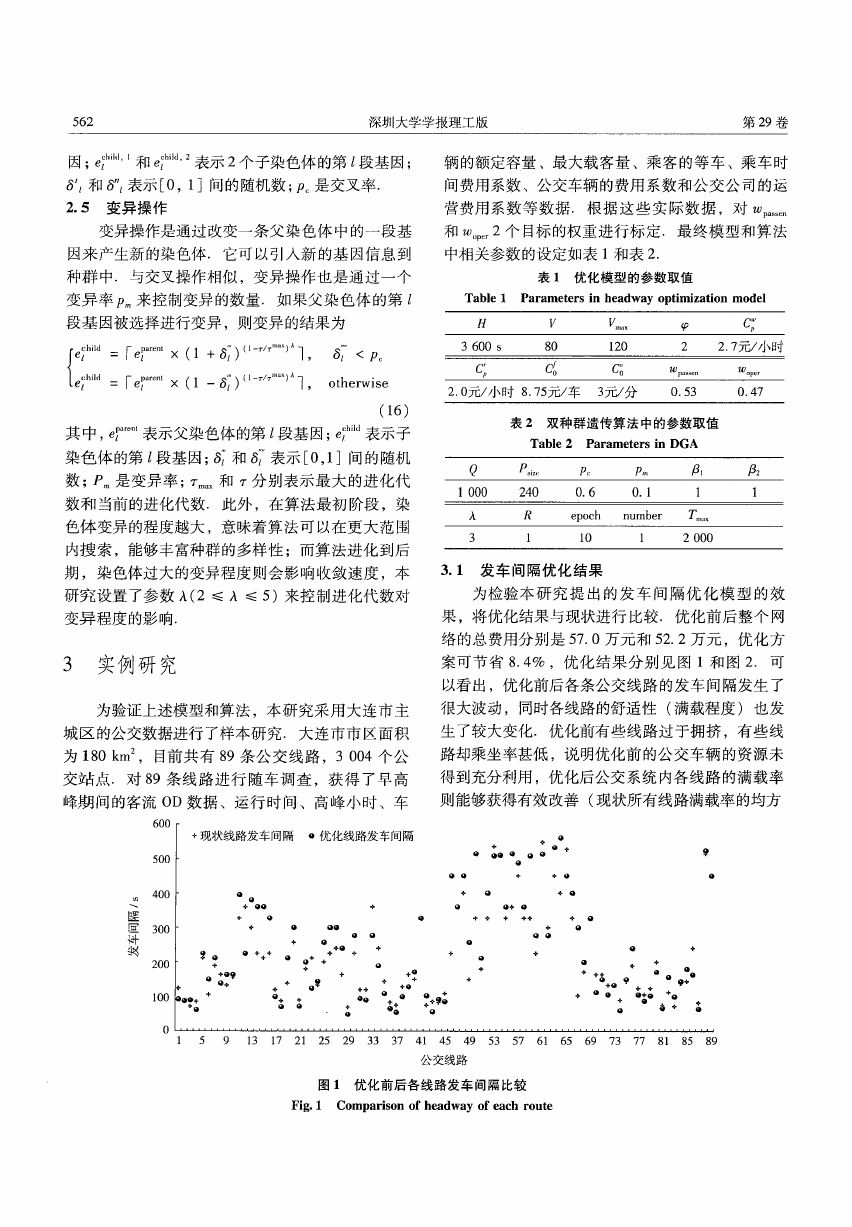1 number β1 β2 Tmax 2000 3.1 发车间隔优化结果 为检验本研究提出的发车间隔优化模型的效 果，将优化结果与现状进行比较.优化前后整个网 络的总费用分别是 57.0 万元和 52. 2 万元，优化方 案可节省 8.4% ，优化结果分别见图 1 和图 2. 可 以看出，优化前后各条公交线路的发车间隔发生了 很大波动，同时各线路的舒适性(满载程度)也发 生了较大变化.优化前有些线路过于拥挤，有些线 路却乘坐率甚低，说明优化前的公交车辆的资源未 得到充分利用，优化后公交系统内各线路的满载率 则能够获得有效改善(现状所有线路满载率的均方 562 因 ;e;lnhl ， l 和 e~俨hil队l 6矶F:t 和 8矶"飞F:l 表示[阳0 ， 1 ]间的随机数 ; PC 是交叉率. 2.5 变异操作 变异操作是通过改变一条父染色体中的一段基 因来产生新的染色体.它可以引人新的基因信息到 种群中.与交叉操作相似，变异操作也是通过一个 变异率 Pm 来控制变异的数量.如果父染色体的第 J 段基因被选择进行变异，则变异的结果为 'hEn tujq 「 l == -A1i (( ×× nn ee rr aa 。 0 m ' ' b 、 l / + 一 (( xx aa nn TT JJJ/ A λ 「l l l ,, δ[ < PC 《 ， 4 r t E F 、 J E l l - ‘ ρ l v ρ t v 已 ， ι 「 l l p a ρ ， u ι P ρ A U F ι 。 。 川m z e b 、 } / T 「l i t otherwise (1 6 ) 其中， efaM 表示父染色体的第 l 段基因 ;efzkl 表示子 染色体的第 l 段基因 ;δl 和 δl 表示 [0 ， 1] 间的随机 数;凡是变异率 'Tmax 和 T 分别表示最大的进化代 数和当前的进化代数.此外，在算法最初阶段，染 色体变异的程度越大，意味着算法可以在更大范围 内搜索，能够丰富种群的多样性;而算法进化到后 期，染色体过大的变异程度则会影响收敛速度，本 研究设置了参数 λ(2 '"二 λ 运 5) 来控制进化代数对 变异程度的影响. 3 实例研究 为验证上述模型和算法，本研究采用大连市主 城区的公交数据进行了样本研究.大连市市区面积 为 180 km2 ，目前共有的条公交线路， 3 004 个公 交站点.对 89 条线路进行随车调查，获得了早高 峰期间的客流 OD 数据、运行时间、高峰小时、车 +现状线路发车间隔 ·优化线路发车间隔 500 400 300 200 Z E E -恃 抖 @+ ·+ @+ +· @+ @ 亨 .+ • 协 +· l nu nu i 陆 • • + ... + .. + Q +. + + + ... . .. .. +. + - : - + -+ ..- +、 + .. + Q .. .. + @ • • • +· + • • +@ • @+ @ • ..+ .. + + + ++ + .. +‘' + .. .. + @+ + @+ + ' • .. • ·+ ·+ .. +@ +· @ +· +@ +· +@ +@ + +· • ·+ -7 ·+ ·+ 4· + • 89 85 81 +- +曹+ + + ø T ~ 't Q Q + Q ++ 0.... "'Q Q -:-‘' 8' -:-. ~+ -'1 .no'!' Q -:- +'a .". Q + 。 5 9 13 17 21 25 29 33 37 41 45 49 公交线路 53 57 61 65 69 73 77 图 1 优化前后备线路发车间隔比较 Fig. 1 Comparison of headway of each route
    第 6 期 姚锦宝，等:基于双种群遗传算法的公交线路发车间隔优化 563 2.0 +现状线路舒适水平 ·优化线路舒适水平 1.6~ + + + + \ l 2 ·+ . . . . …+ 叶 怜明越E + 9 .@ 0080+ ~ Q 0 0 + Q . G+ 4b 0 + _+ o 品! + + 4· • + + • • +@ +· O 8+ .+++ + + + + + • + + +· +· • • • ·+ @ • • ·+ ·+ @+ ·+ • • ·+ • ·+ +· ·+ • + • • + @+ @+ @+ + @+ @ + +@ +· • azT • • , ·+ • + +++ • • • +· ·+ + + ·+ • • +· + + 00 + • • @ + O.4 r 。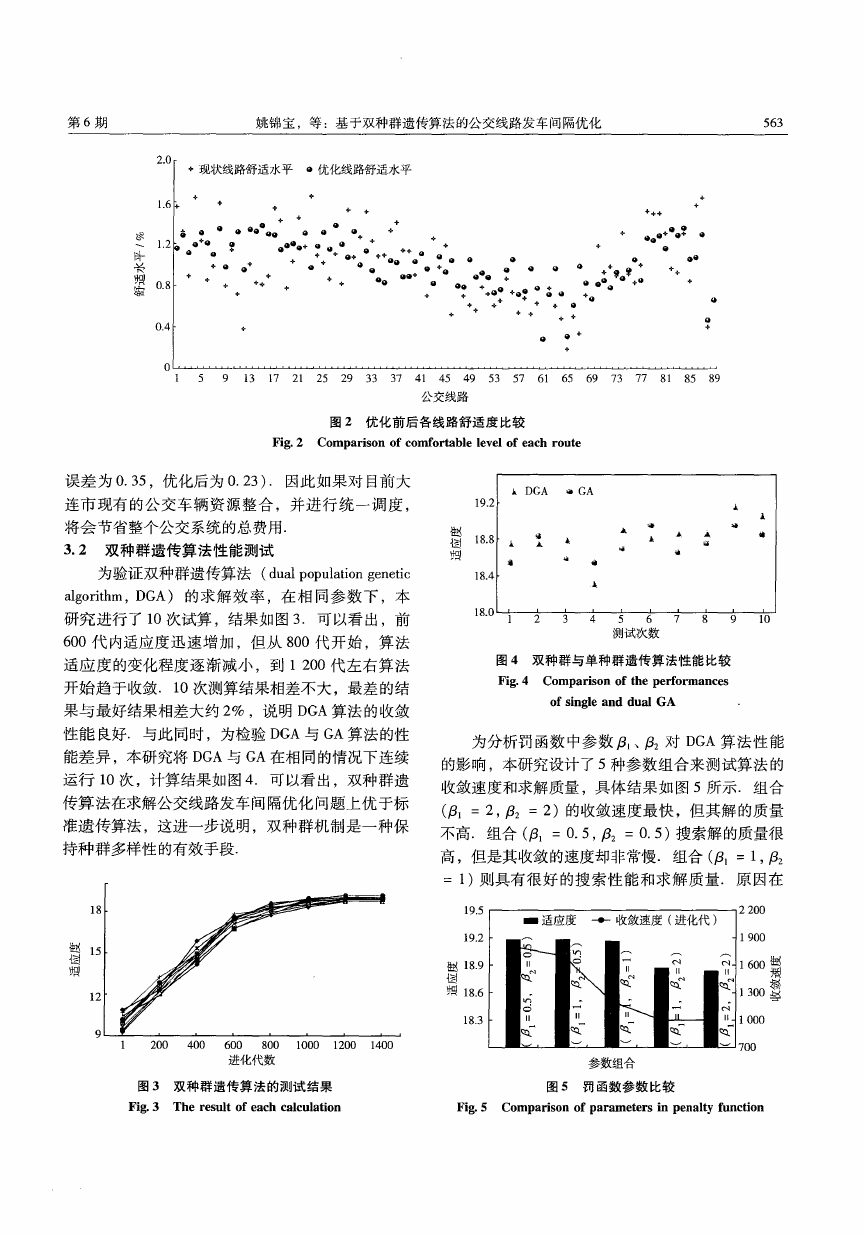 + + + + + + 00+ + 5 9 13 17 21 25 29 33 37 41 45 49 53 57 61 65 69 73 77 81 85 89 公交线路 圄 2 优化前后各线路舒适度比较 Fig. 2 Comparison of comfortable level of each route 误差为 0.35 ，优化后为 0.23) .因此如果对目前大 连市现有的公交车辆资源整合，并进行统一调度， 将会节省整个公交系统的总费用. 3.2 双种群遗传算法性能测试 为验证双种群遗传算法( dual population genetic algorithm , DGA) 的求解效率，在相同参数下，本 研究进行了 10 次试算，结果如图 3. 可以看出，前 600 代内适应度迅速增加，但从 800 代开始，算法 适应度的变化程度逐渐减小，到 1 200 代左右算法 开始趋于收敛 .10 次测算结果相差不大，最差的结 果与最好结果相差大约 2% ，说明 DGA 算法的收敛 性能良好.与此同时，为检验 DGA 与 GA 算法的性 能差异，本研究将 DGA 与 GA 在相同的情况下连续 运行 10 次，计算结果如图 4. 可以看出，双种群遗 传算法在求解公交线路发车间隔优化问题上优于标 准遗传算法，这进一步说明，双种群机制是一种保 持种群多样性的有效手段. 18 自 15 明 12 9 200 400 800 600 进化代数 1000 1200 1400 圄 3 双种群遗传算法的测试结果 Fig. 3 The result of each calculation .. DGA '" GA 19.2~ A 喝 ' • A 日画 ~ 也 .. a @ A • 句画 • A 生吕 因F司 18.8 18.4 18.0 .. • A .. 2 3 4 6 5 测试次数 7 8 9 10 图 4 双种群与单种群遗传算法性能比较 Fig. 4 Comparison of the perfonnances of single and dual GA 为分析罚函数中参数 βl 、 β2 对 DGA 算法性能 的影响，本研究设计了 5 种参数组合来测试算法的 收敛速度和求解质量，具体结果如图 5 所示.组合 (β2 ， β2 = 2) 的收敛速度最快，但其解的质量 不高.组合 (β1 = 0.5 ， β2 = 0.5) 搜索解的质量很 高，但是其收敛的速度却非常惶组合 (β1β2 = 1) 则具有很好的搜索性能和求解质量.原因在 ·适应度 ........收敛速度(进化代) 2200 1900 .:: 19.5 19.2 刨 18.9 国 甘冒 18.6 18.3 T~白ld V4P 3 11 CQ.. 参数组合 圄 5 罚函数参数比较 Fig. 5 Comparison of parameters in penalty function
    564 深圳大学学报理工版 第 29 卷 于，随着 2 个参数的增大，罚函数对违背约束的染 色体进行了更加严厉的惩罚，使其很快从种群中消 失.但是，由于搜索方案很容易产生一些不满足约 束的解方案，这些方案虽然违背约束但是其很可能 会存在部分有益的基因段，如果过快淘汰这些基因 可能会影响求解的质量.因此，对于进化过程中， 容易产生不可行方案的 DGA 应该考虑采用较大的 控制参数(乱， β2) ;反之，则应选择较小的参数. 结语 发车间隔优化对公交运营至关重要，本研究从 乘客和公交运营者双方利益出发，考虑城市公交车 辆资源的约束，开发了一个同时考虑乘客时间费用 和运营者费用最低的发车间隔优化模型.考虑到该 模型属于公交调度问题，设计了双种群遗传算法对 其进行了求解.以大连市主城区公交系统的数据对 该模型和算法进行了检验.结果显示，如果对大连 市公交车辆资源进行整合，统一调度会改善整个系 统的服务水平，同时也可以降低系统的总成本.此 外，通过与标准的遗传算法进行比较表明，双种群 遗传算法的求解效果优于标准遗传算法. 基金项目:国家自然科学基金资助项目 (51208079 ， 51108053) 作者简介:姚锦宝 (1972-) ，男(汉族) .安徽省安庆市人，北京 交通大学讲师、博士. E-mail: jbyao@bjtu.edu.cn 引 文:姚锦宝，姚宝珍，尹智宏，等.基于双种群遗传算法的 公交线路发车间隔优化[1].深圳大学学报理工版， 2012 , 29(6): 559δ64. 参考文献/References: [ 1 J Scheele S. A supply model for public transit services [ 1]. Transportation Research: B , 1980 , 14: 133 -146. [ 2 J Sun C J , Zhou W , Wang Y Q. Scheduling combination and headway optimization of bus rapid transit [J J. Jour nal of Transportation Systems Engineering and Information Technology , 2008 , 8 (5) : 61 -67. [ 3 ] Tom V M, Mohan S. Transit route network design using frequency coded genetic algorithm [J J. J Transp Een asce , 2003 , 129(2): 186-195. [ 4 ] Park S J. Bus Network Scheduling with Genetic Algorithms and Simulation [D J. Maryland (USA): University of Marγland ， 2005. [ 5 ] YANG Zhao-sheng. Theory and Method of Urban Intelli gent Public Transportation System [M J. Beiji吨 Railway Press , 2002: 56-76. ( in Chinese) 杨兆升城市智能公共交通系统理论与方法[ MJ 北京:中国铁道出版社， 2002: 56-76. [ 6 J SONG Rui , HE Shi-wei , YANG Hai , et al. Optimal tran sit operation plan model and algorithm with stochastic OD demands [J J. China Civil Engineering Joumal , 2006 , 39 (4): 110-115. (in Chinese) 宋瑞，何世伟，杨海，等.基于随机需求的公交运 营设计优化模型及算法[J J. 土木工程学报， 2006 , 39( 4): 110-115. [ 7 ] YU Bin , Y ANG Zhong-zhen , CHENG Chun-tian , et al. Bi-level programming model for optimizing bus frequencies and its algorithm [J J. Joumal of Jilin University Engi neering and Technology Edition , 2006 , 36 (5) : 664-668. (in Chinese) 于 滨，杨忠振，程春田，等.公交线路发车频率优化 的双层规划模型及其解法[1] .吉林大学学报工学 版， 2006 , 36 (5): 664-668 [ 8 J CAI Liang-wei , HU Shi-xi. A genetic algorithm based on similarity and its application on JSP [J J. Joumal of Shenzhen University Science and Engineering , 2006 , 23 (2): 107-11 1. (in Chinese) 蔡良伟，胡世曦-基于相似性遗传算法及其在 JSP 中 的应用[ J J .深圳大学学报理工版， 2006 , 23 (2): 107 -11 1. [ 9 J WU Xu-yi , WU Xiao-yu. Improved genetic algorithm for job-shop scheduling [J J. Joumal of Shenzhen University Science and Engineering , 2006 , 23 ( 3 ): 272-277. (in Chinese) 吴序一，伍晓宇.非量产模式下车间调度的改进遗传 算法[J] .深圳大学学报理工版， 2006 , 23 ( 3 ) : 272-277. [ 10 J Zhao G H , Shen W H , Wu M L. Ultra-wideband antenna design using FDTD and double population genetic algo rithm [J J. Microwave and Optical Technology Letters , 2009 , 51 (2) : 361-364. [ 11 J Holland J H. Adaptation in Natural and Artificial Systems [ M J. Michigan (USA): University of Michigan Press , 1975.234-245. [12J LI Bi , LIN Tu-she吨. Modified genetic algorithm based on competitive coevolution [J J. Joumal of Shenzhen Univer sity Science and Engineering , 2009 , 26 ( 1 ): 24-29. (in Chinese) 李 碧，林土胜.基于竞争协同进化的改进遗传算法 [J].深圳大学学报理工版， 2009 , 26 (1): 24-29. [ 13 J CAI Liang-wei. Real-coded adaptive genetic annealing al gorithm based on distance measurement [J J. Joumal of Shenzhen University Science and Engineering , 2004 , 21 (4): 291-294. (in Chinese) 蔡良伟.基于距离视~度的实数编码自适应遗传退火算 法 [JJ. 深圳大学学报理工版， 2004 ， 21 (4): 291- 294. [中文责编:坪梓;英文责编:之幸]
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料