logo资料库

DSPII计算机作业2.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.91M 资料格式：pdf 举报 版权申诉
第1页 / 共19页
第2页 / 共19页
第3页 / 共19页
第4页 / 共19页
第5页 / 共19页
第6页 / 共19页
第7页 / 共19页
第8页 / 共19页
资料共19页，剩余部分请下载后查看
    1. Consider an AR process x(n) defined by the difference equation where v(n) is an additive white noise of zero mean and variance .The AR parameters and are both real valued: a) Calculate the noise variance such that the AR process x(n) has unit variance .Hence , generate different realization of the process x (n). b) Given the input x (n), an LMS filter of length M = 2 is used to estimate the unknown AR parameters and . The step size is assigned the value 0.05. Compute and plot the ensemble average curve of and by averaging the value of parameters and over an ensemble of 100 different realization of the filter. Calculate the time constant according to the experiment results and compare with the corresponded theoretical value. c) For one realization of the LMS filter, compute the prediction error And the two tap-weight errors and Using power spectral plots of , show that f(n) behaves as white noise, whereas and behave as low-pass process. Explain the reason for this phenomenon. d) Compute the ensemble average learning curve of the LMS filter by averaging the square value of the prediction error f(n) over an ensemble of 100 different realization of the filter. Calculate the time constant and residual power according to the experiment results and compare with the corresponded theoretical values. 12()(1)(2)()xnaxnaxnvn2v1a2a120.10.8aa2v1a2a1a2a1a2a()()()fnxnxn111()()nahn222()()nahn12(),() ()fnnandn1() n2() n
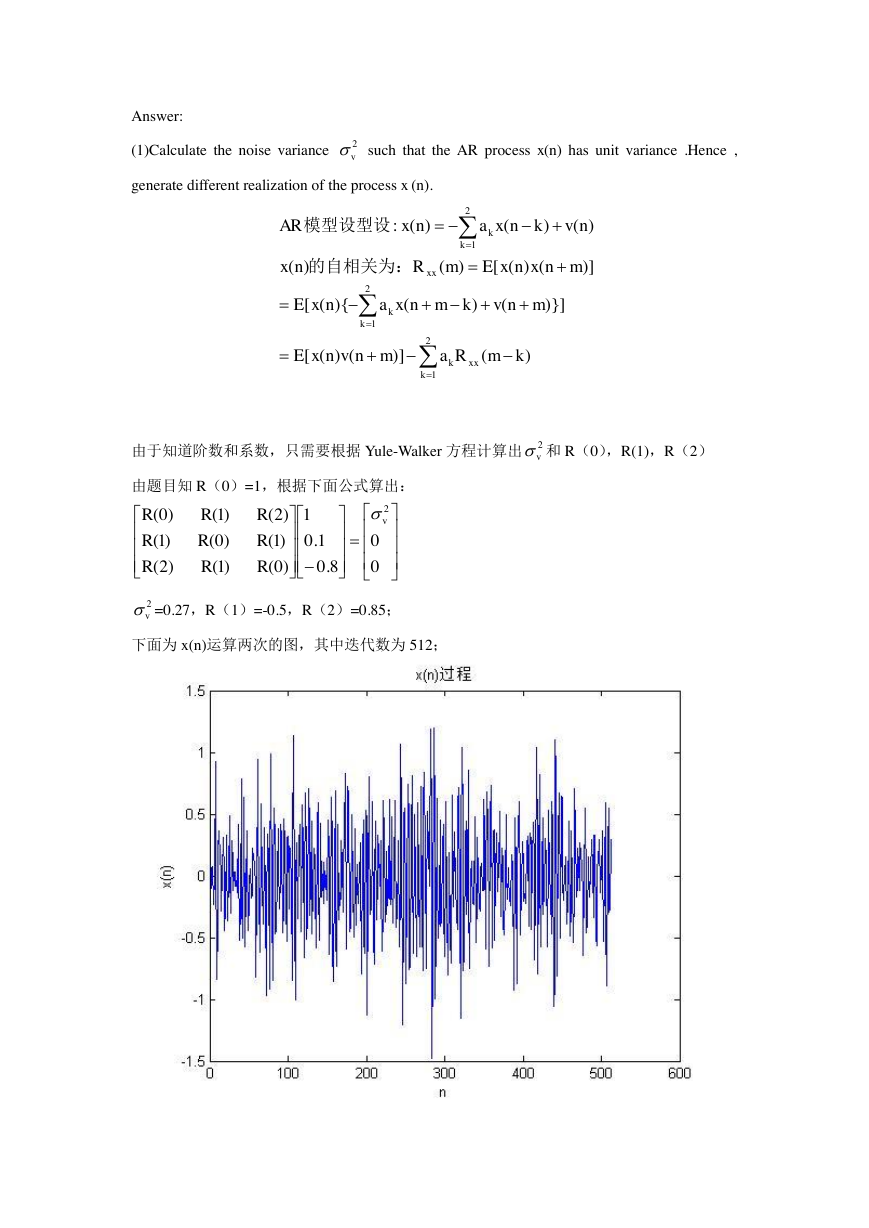
    Answer: (1)Calculate the noise variance such that the AR process x(n) has unit variance .Hence , generate different realization of the process x (n). 由于知道阶数和系数，只需要根据 Yule-Walker 方程计算出 和 R（0），R(1)，R（2） 由题目知 R（0）=1，根据下面公式算出： =0.27，R（1）=-0.5，R（2）=0.85； 下面为 x(n)运算两次的图，其中迭代数为 512； 2v2v008.01.01)0()1()2()1()0()1()2()1()0(2vRRRRRRRRR2v)(R)]()([)}]()(){([)]()([)(R)()()()(:模型设型设ARxx2121xx21kmamnvnxEmnvkmnxanxEmnxnxEmnxnvknxanxkkkkkk的自相关为：
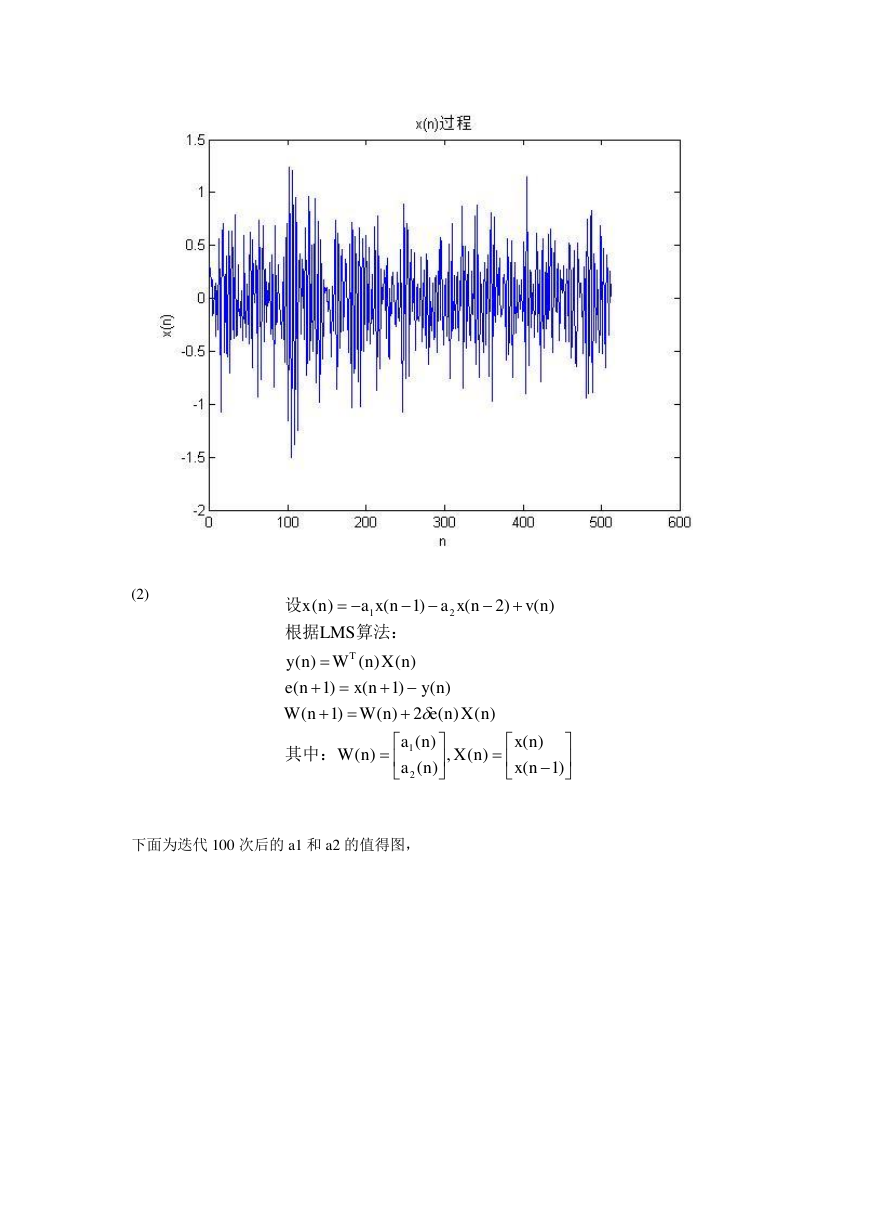
    (2) 下面为迭代 100 次后的 a1 和 a2 的值得图， )1()()(,)()()()()(2)()1()()1()1()()()(yLMS)()2()1()n(x2121nxnxnXnananWnXnenWnWnynxnenXnWnnvnxanxaT其中：算法：根据设
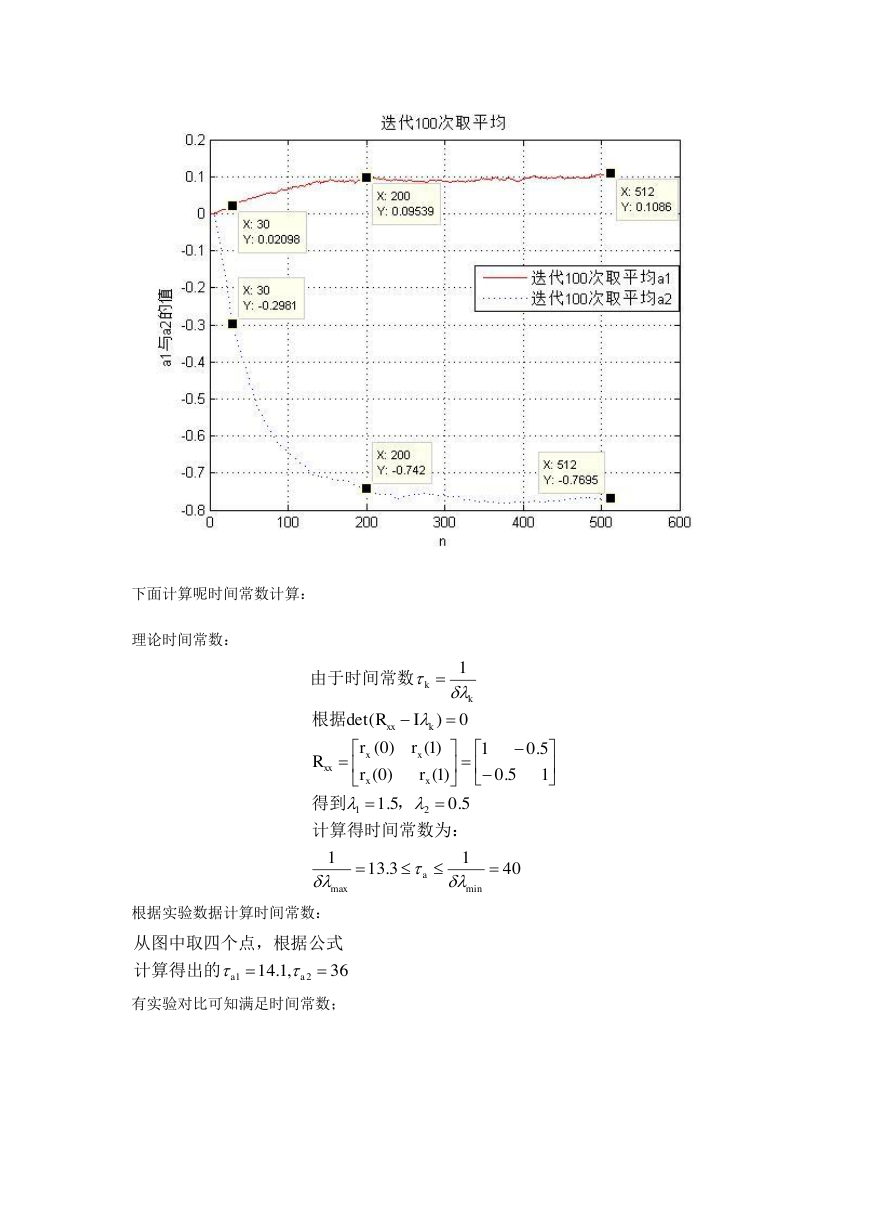
    下面计算呢时间常数计算： 理论时间常数： 根据实验数据计算时间常数： 有实验对比可知满足时间常数； 4013.1315.05.115.05.01)1()0()1()0(0)(det1minmax21kaxxxxxxkxxkrrrrRIR计算得时间常数为：，得到根据由于时间常数36,1.142a1a计算得出的公式从图中取四个点，根据
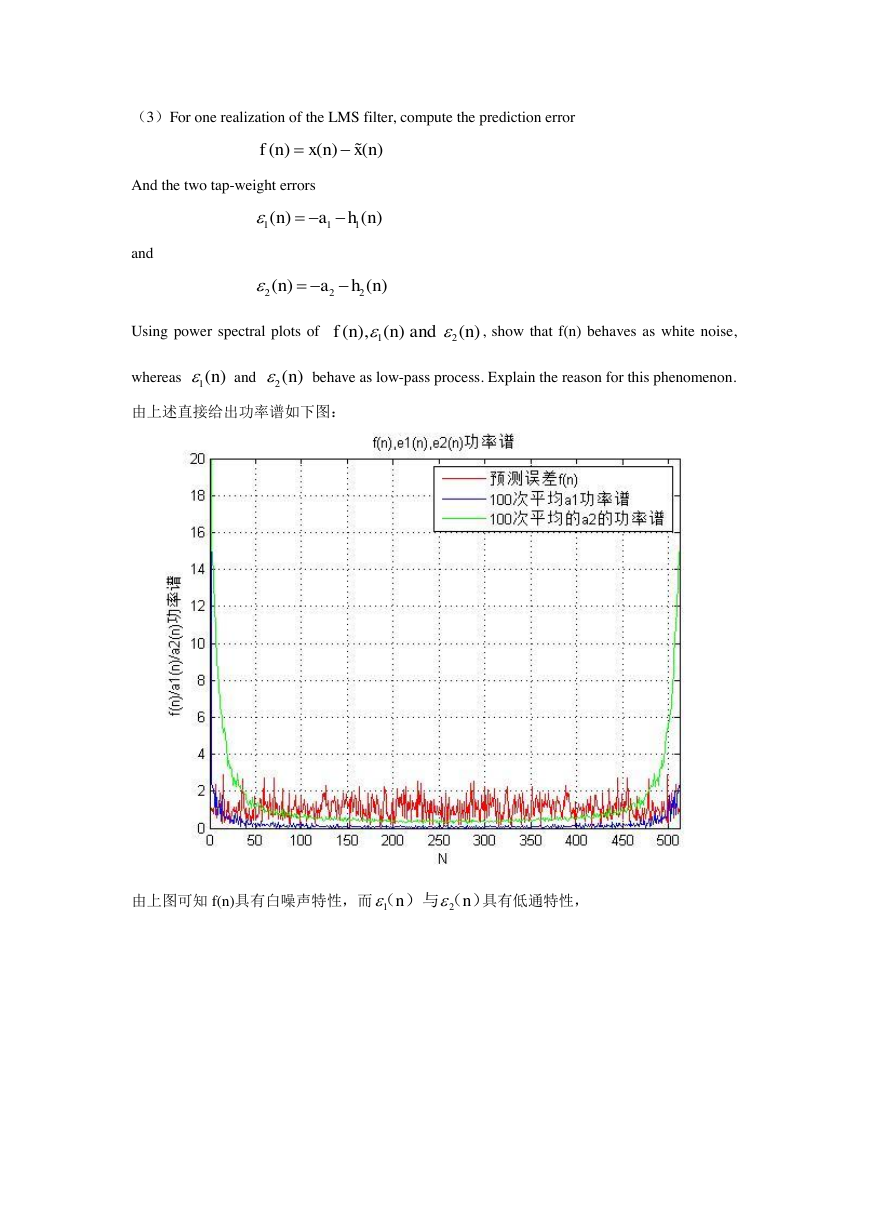
    （3）For one realization of the LMS filter, compute the prediction error And the two tap-weight errors and Using power spectral plots of , show that f(n) behaves as white noise, whereas and behave as low-pass process. Explain the reason for this phenomenon. 由上述直接给出功率谱如下图： 由上图可知 f(n)具有白噪声特性，而 具有低通特性， ()()()fnxnxn111()()nahn222()()nahn12(),() ()fnnandn1() n2() n）（）与（nn21
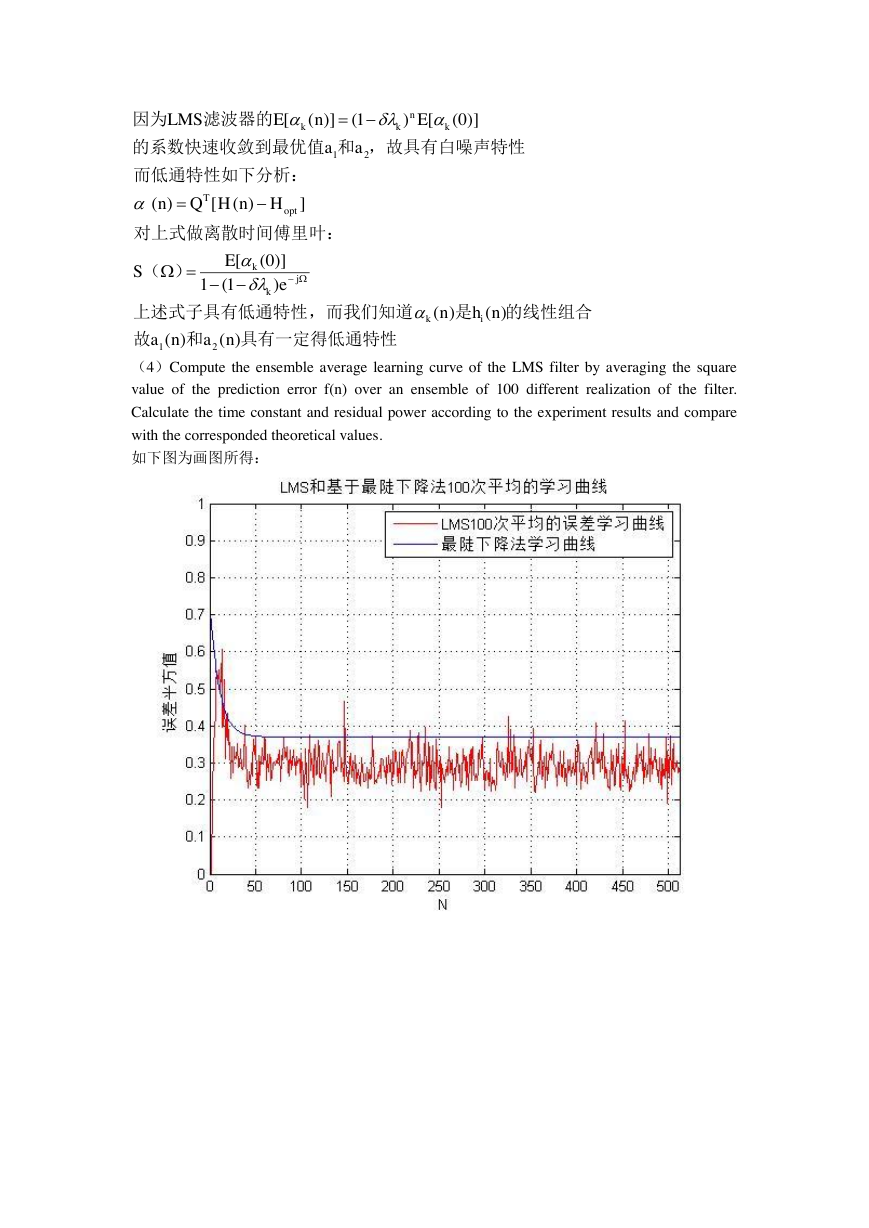
    （4）Compute the ensemble average learning curve of the LMS filter by averaging the square value of the prediction error f(n) over an ensemble of 100 different realization of the filter. Calculate the time constant and residual power according to the experiment results and compare with the corresponded theoretical values. 如下图为画图所得： 具有一定得低通特性和故的线性组合是，而我们知道上述式子具有低通特性）（叶：对上式做离散时间傅里而低通特性如下分析：，故具有白噪声特性和值的系数快速收敛到最优滤波器的因为)()()()n()1(1)]0([ES])([Q)(a)]0([E)1()]([ELMS21T21nananheHnHnanikjkkoptknkk
    由上图任取两个值进行实验和理论值得比较： 根据公式： 综述实验和理论计算基本吻合。 2. 设 是窄带信号，定义 是在 区间上均匀分布的随机相位。 是寬带信号，它是一个零均值、方差为 1 的白噪音信号 e(n)激励一个线性滤波器而产生，其差分方程为 。 1） 计算 和 各自的自相关函数，并画出其函数图形。根据此选择合适的延 时，以实现谱线增强。 2） 产生一个 序列。选择合适的 值。让 通过谱线增强器。画出输出信号 和误差信号 e(n)的波形，并分别与 和 比较。 （1）计算 和 各自的自相关函数，并画出其函数图形。根据此选择合适的延时， 以实现谱线增强。 ;37.0,284.0J;2)2()1(,)0()1()1()0(R,)0()21/(JJ;1021LMSminxx1xxmin2minkJNrrrrrrrrRHrHRJNxxyxxxxxyxoptyxToptxk）（方收敛误差为由上述计算出的理论均，）（均方收敛后的误差为：：理论上均分时间收敛为算法性能分析可知：根据49.93029.0395214.016288.0])([)(JJJJNJeJnJNn，；取实验数据121()()(),()xnxnxnxn1()sin(0.05),xnn[0,2]2()xn2()()2(1)(2)xnenenen1()xn2()xn()xn()xn()yn1()xn2()xn1()xn2()xn
    下面为画出的图形： 由上图可知道，LMS 参考信号中的宽带成分在延时因子 D 大于等于 3 后与输入的宽带信号 成分不相关。而窄带信号依然具有相关性，因此通过 LMS 滤波有效的增强一定幅度。 （2）产生一个 序列。选择合适的 值。让 通过谱线增强器。画出输出信号 和误差信号 e(n)的波形，并分别与 和 比较。 我们知道噪声的平均功率远大于正弦的平均功率，所以为了实现谱线增强需要选取合适的滤 波阶数和迭代步长； 首先分析滤波器阶数： 当滤波器阶数较小时误差信号可以收敛到 ，而 不能很好收敛到 而迭代步长： 我们知道迭代步长越小，精度大但收敛慢，而迭代大了，精度小，收敛快 )2()1(4)(6)1(4)2()}]2()1(2)()}{2()1(2)([{E)]()([)()()05.0cos(21)]2)2(05.0cos()05.0[cos(21)])(05.0sin()05.0[sin()]()([)()(22221111kkkkkkneknekneneneneknxnxEkrnxkknkEknnEknxnxEkrnxxx得自相关然后计算的自相关：先计算()xn()xn()yn1()xn2()xn2()xn()yn1()xn
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料