logo资料库

Matlab Robotics工具箱使用说明.docx

发布时间：2022-06-10 发布人：admin 分类：说明书 资料大小：0.32M 资料格式：docx 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    robotic toolbox for matlab 工具箱下载地址： http://download.csdn.net/source/940770 1. PUMA560 的 MATLAB 仿真 要建立 PUMA560 的机器人对象，首先我们要了解 PUMA560 的 D-H 参数， 之后我们可以利用 Robotics Toolbox 工具箱中的 link 和 robot 函数来建立 PUMA560 的机器人对象。 其中 link 函数的调用格式： L = LINK([alpha A theta D]) L =LINK([alpha A theta D sigma]) L =LINK([alpha A theta D sigma offset]) L =LINK([alpha A theta D], CONVENTION) L =LINK([alpha A theta D sigma], CONVENTION) L =LINK([alpha A theta D sigma offset], CONVENTION) 参数 CONVENTION 可以取‘standard’和‘modified’，其中‘standard’代表 采用标准的 D-H 参数，‘modified’代表采用改进的 D-H 参数。参数‘alpha’ 代表扭转角 ，参数‘A’代表杆件长度，参数‘theta’代表关节角，参数‘D’ 代表横距，参数‘sigma’代表关节类型：0 代表旋转关节，非 0 代表移动关节。 另外 LINK 还有一些数据域： %返回横距 %返回关节类型 %返回‘R’(旋转)或‘P’(移动) %返回扭转角 %返回杆件长度 %返回关节角 LINK.alpha LINK.A LINK.theta LINK.D LINK.sigma LINK.RP %若为标准 D-H 参数返回 0，否则返回 1 LINK.mdh %返回关节变量偏移 LINK.offset LINK.qlim %返回关节变量的上下限 [min max] LINK.islimit(q) %如果关节变量超限，返回 -1, 0, +1 LINK.I %返回一个 3×3 对称惯性矩阵
    %返回关节质量 %返回 3×1 的关节齿轮向量 %返回齿轮的传动比 LINK.m LINK.r LINK.G LINK.Jm %返回电机惯性 LINK.B %返回粘性摩擦 LINK.Tc %返回库仑摩擦 LINK.dh LINK.dyn return legacy DH row return legacy DYN row 其中 robot 函数的调用格式： %创建一个空的机器人对象 %创建 robot 的一个副本 ROBOT ROBOT(robot) ROBOT(robot, LINK) %用 LINK 来创建新机器人对象来代替 robot ROBOT(LINK, ...) ROBOT(DH, ...) ROBOT(DYN, ...) %用 LINK 来创建一个机器人对象 %用 D-H 矩阵来创建一个机器人对象 %用 DYN 矩阵来创建一个机器人对象 2．变换矩阵 利用 MATLAB 中 Robotics Toolbox 工具箱中的 transl、rotx、roty 和 rotz 可以实 现用齐次变换矩阵表示平移变换和旋转变换。下面举例来说明： A 机器人在 x 轴方向平移了 0.5 米，那么我们可以用下面的方法来求取平移变换 后的齐次矩阵： >> transl(0.5,0,0) ans = 1.0000 0 0 0 0 1.0000 0 0 0 0 1.0000 0 0.5000 0 0 1.0000 B 机器人绕 x 轴旋转 45 度，那么可以用 rotx 来求取旋转后的齐次矩阵： >> rotx(pi/4) ans = 1.0000 0 0 0
    0 0 0 0.7071 0.7071 0 -0.7071 0.7071 0 0 0 1.0000 C 机器人绕 y 轴旋转 90 度，那么可以用 roty 来求取旋转后的齐次矩阵： >> roty(pi/2) ans = 0.0000 0 -1.0000 0 0 1.0000 0 0 1.0000 0 0.0000 0 0 0 0 1.0000 D 机器人绕 z 轴旋转-90 度，那么可以用 rotz 来求取旋转后的齐次矩阵： >> rotz(-pi/2) ans = 0.0000 -1.0000 0 0 1.0000 0.0000 0 0 0 0 1.0000 0 0 0 0 1.0000 当然，如果有多次旋转和平移变换，我们只需要多次调用函数在组合就可以了。 另外，可以和我们学习的平移矩阵和旋转矩阵做个对比，相信是一致的。 3 轨迹规划 利用 Robotics Toolbox 提供的 ctraj、jtraj 和 trinterp 函数可以实现笛卡尔规划、关 节空间规划和变换插值。 其中 ctraj 函数的调用格式： TC = CTRAJ(T0, T1, N) TC = CTRAJ(T0, T1, R) 参数 TC 为从 T0 到 T1 的笛卡尔规划轨迹，N 为点的数量，R 为给定路径距 离向量，R 的每个值必须在 0 到 1 之间。 其中 jtraj 函数的调用格式： [Q QD QDD] = JTRAJ(Q0, Q1, N)
    [Q QD QDD] = JTRAJ(Q0, Q1, N, QD0, QD1) [Q QD QDD] = JTRAJ(Q0, Q1, T) [Q QD QDD] = JTRAJ(Q0, Q1, T, QD0, QD1) 参数 Q 为从状态 Q0 到 Q1 的关节空间规划轨迹，N 为规划的点数，T 为给 定的时间向量的长度，速度非零边界可以用 QD0 和 QD1 来指定。QD 和 QDD 为返回的规划轨迹的速度和加速度。 其中 trinterp 函数的调用格式： TR = TRINTERP(T0, T1, R) 参数 TR 为在 T0 和 T1 之间的坐标变化插值，R 需在 0 和 1 之间。 要实现轨迹规划，首先我们要创建一个时间向量，假设在两秒内完成某个动作， 采样间隔是 56ms，那么可以用如下的命令来实现多项式轨迹规划：t=0:0.056:2; [q,qd,qdd]=jtraj(qz,qr,t); 其中 t 为时间向量，qz 为机器人的初始位姿，qr 为机器人的最终位姿，q 为经过 的路径点，qd 为运动的速度，qdd 为运动的加速度。其中 q、qd、qdd 都是六列 的矩阵，每列代表每个关节的位置、速度和加速度。如 q(:,3)代表关节 3 的位置， qd(:,3)代表关节 3 的速度，qdd(:,3)代表关节 3 的加速度。 4 运动学的正问题 利用 Robotics Toolbox 中的 fkine 函数可以实现机器人运动学正问题的求解。 其中 fkine 函数的调用格式： TR = FKINE(ROBOT, Q) 参数 ROBOT 为一个机器人对象，TR 为由 Q 定义的每个前向运动学的正 解。 以 PUMA560 为例，定义关节坐标系的零点 qz=[0 0 0 0 0 0]，那么 fkine(p560,qz) 将返回最后一个关节的平移的齐次变换矩阵。如果有了关节的轨迹规划之后，我 们也可以用 fkine 来进行运动学的正解。比如： t=0:0.056:2; q=jtraj(qz,qr,t); T=fkine(p560,q); 返回的矩阵 T 是一个三维的矩阵，前两维是 4×4 的矩阵代表坐标变化，第三维 是时间。 5 运动学的逆问题
    利用 Robotics Toolbox 中的 ikine 函数可以实现机器人运动学逆问题的求解。 其中 ikine 函数的调用格式： Q = IKINE(ROBOT, T) Q = IKINE(ROBOT, T, Q) Q = IKINE(ROBOT, T, Q, M) 参数 ROBOT 为一个机器人对象，Q 为初始猜测点（默认为 0），T 为要反解的 变换矩阵。当反解的机器人对象的自由度少于 6 时，要用 M 进行忽略某个关节 自由度。 有了关节的轨迹规划之后，我们也可以用 ikine 函数来进行运动学逆问题的求解。 比如： t=0:0.056:2; T1=transl(0.6,-0.5,0); T2=transl(0.4,0.5,0.2); T=ctraj(T1,T2,length(t)); q=ikine(p560,T); 我们也可以尝试先进行正解，再进行逆解，看看能否还原。 Q=[0 –pi/4 –pi/4 0 pi/8 0]; T=fkine(p560,q); qi=ikine(p560,T); 6 动画演示 有了机器人的轨迹规划之后，我们就可以利用 Robotics Toolbox 中的 plot 函数来 实现对规划路径的仿真。 puma560;T=0:0.056:2; q=jtraj(qz,qr,T); plot(p560,q); 当然，我们也可以来调节 PUMA560 的六个旋转角，来实现动画演示。 drivebot(p560)
    至于 Matlab 工具箱安装中涉及到了 Matlab 的搜索路径、工作目录、当前路径、用户路径等 好多术语，我这里不想多说什么 感兴趣的网友，可以直接查看 Matlab 的帮助系统，在那里你可以得到最直接的答复，但是 你需要一定的英文基础哦 添加工具箱的方法很多，所有方法都是为了达到同一个目的，将工具箱的所在路径添加到 Matlab 的搜索路径下就可以了 下面介绍一种最简单的操作吧，下面以安装 mathmodl(数学建模工具箱)为例进行说明 a、将你所需要安装的工具箱解压到$MatlabRoot\toolbox 中(其实任意路径都是可以的，但 是为了方便管理，我们一般都安装在这里)，$MatlabRoot 是你的 Matlab 安装路径，你可以 在 Matlab 中输入 matlabroot 命令获取 (1)在 Matlab 输入如下内容(当然你可以直接使用资源管理器进入 toolbox 目录) ans = 1. >> matlabroot 2. 3. 4. 5. D:\Program Files\MATLAB\R2008a 6. 7. >> winopen(ans) 复制代码 (2)此时会自动跳到 Matlab 的安装目录下，双击打开目录下的 toolbox 文件夹 (3)将 mathmodl 工具箱复制到 toolbox 中
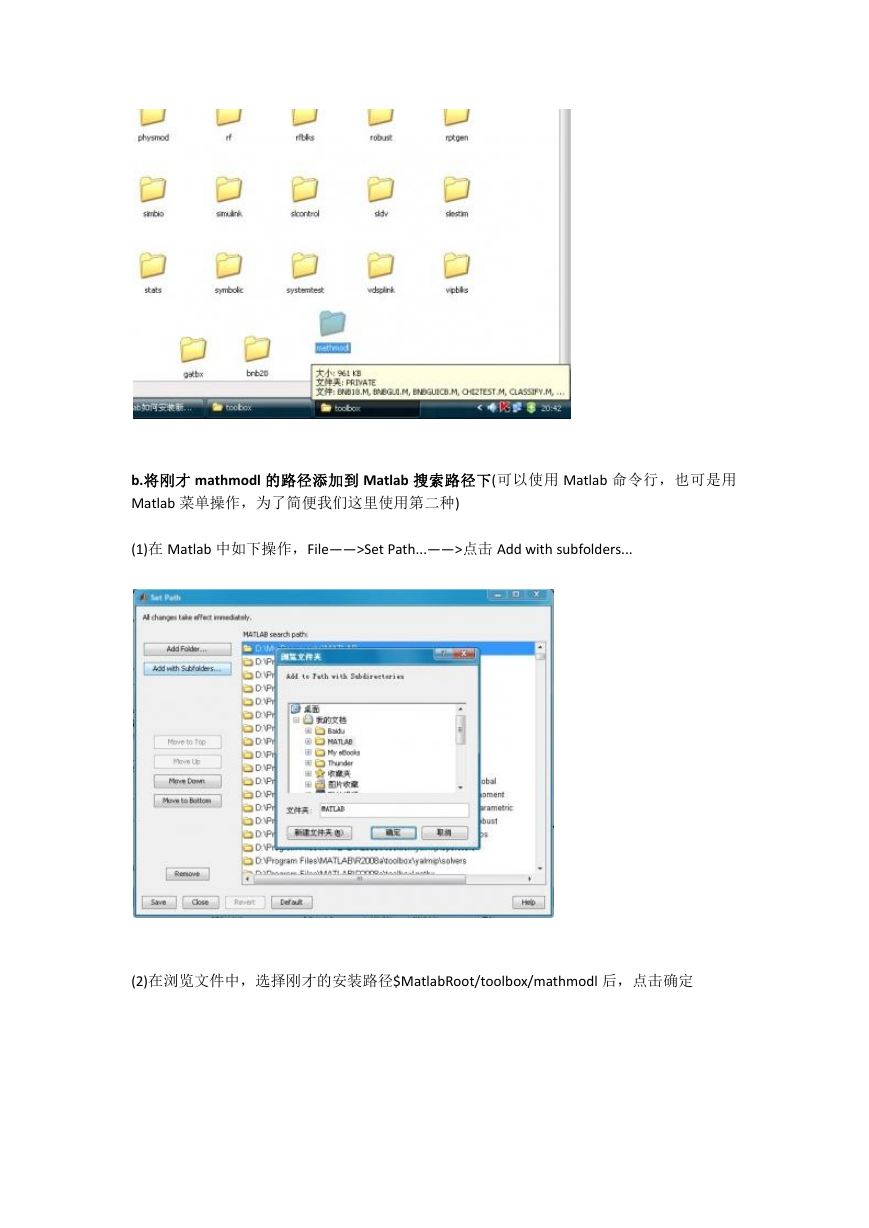
    b.将刚才 mathmodl 的路径添加到 Matlab 搜索路径下(可以使用 Matlab 命令行，也可是用 Matlab 菜单操作，为了简便我们这里使用第二种) (1)在 Matlab 中如下操作，File——>Set Path...——>点击 Add with subfolders... (2)在浏览文件中，选择刚才的安装路径$MatlabRoot/toolbox/mathmodl 后，点击确定
    (3)此时返回到 Set Path 对话框，点击左下角的保存按钮(记住一定要保存)，此时工具箱彻底 安装完毕，点击 Close 关闭对话框 c.测试下新安装工具箱是可以使用，在 Matlab 中输入如下内容 1. >>help mathmodl%输入工具箱名称，此时一般会返回该工具箱的说明，也就是 mathmodl 路径下 content.m 中的内容 2. %在命令行中输入如下，此时会返回 mathmodl 路径下所有的文件 3. >>what mathmodl 4. %再到 mathmodl 中随便找一个不与 Matlab 中重名的函数，比如 DYNPROG.M，在命 令行中输入 5. >>which DYNPROG.M 6. 7. D:\My Documents\MATLAB\DYNPROG.M 复制代码 d.工具箱更新缓存，否则每次 Matlab 启动的时候会给出警告 (1)File——>Preferences——>General——> 选 中 enable toolbox path cache——> 点 击 updata toolbox path cache
    分享到：
    赞 收藏

    相关推荐

    资料库

    网络技术

    共收录2367份资料，累计7个分类，关注成员有19位，主要包括：综合布线,网管软件,网络监控,网络设备,其它,系统集成,网络基础

    热门标签

    综合布线 网管软件 网络监控 网络设备 其它 系统集成 网络基础

    最新资料