第1页 / 共25页
第2页 / 共25页
第3页 / 共25页
第4页 / 共25页
第5页 / 共25页
第6页 / 共25页
第7页 / 共25页
第8页 / 共25页
VCC工具的手册.pdf
Introduction
Terminology
Overview
Preprocessing
Syntax
Annotations
Types
Integral Types
Record Types
Map Types
Inductive Types
Pointers
Pointer Sets
Objects
Special Forms in Invariants
States
Threads
Compound Types
Ghost Fields
Invariants
Structs
Unions
Array Object Types
Blobs
Claims
Declarations
Purely Local Variables
Global Variable Declarations
Function Declarations
Function Declarations
Ghost Parameters
Atomic Inline Functions
Pure Functions
Custom Admissibility Checks
Termination
Expressions
Logical Operators
Quantifications
Function Calls
Statements
Wrapping and Unwrapping
Unwrapping Blocks
Expression Statements
Block Contracts
Assertions and assumptions
Ghost Statements
Iterative Statements
Atomic Actions
Closed Object Lists
Ghost Atomic Actions
Atomic Blocks
Atomic Operations
Verifying Functions
Utility Functions
Macros
Inference
Triggering
Debugging
Smoke Tests
Verification Switches
Caveats
The VCC Manual
Working draft, version 0.2, August 20, 2012
This manual presents the annotation language of VCC, a deductive verifier for concurrent C code.
Abstract
1 Introduction
VCC is a deductive verifier for concurrent C code. VCC takes C code, annotated with function contracts, loop invariants, data invariants,
ghost data, and ghost code, and tries to verify that the code respects these annotations. This manual describes these annotations in
detail, and what constitutes correct verification behavior of VCC. It does not describe in detail the actual implementation of VCC.
1.1 Terminology
VCC means either the VCC tool or the language in which the annotations are written (which is an extension of C), depending on
context. Text in this typeface is written in this language, with the exception of text enclosed within angle brackets which is used to
give an English description of a command or value or values within such a text, e.g. x == . Mathematical
formulas are written as VCC expressions, and models of portions of the state are written as VCC types (with occasional liberties as noted
in the text).
In this document, we consider the meaning of a fixed, annotated program, which we refer to as the program. The unannotated
program means the annotated program stripped of all VCC annotations (i.e., the program as seen by the C compiler).
Due to an unfortunate historical legacy, the VCC type \object corresponds to what are in this document called pointers, whereas
the word “object” means a particular subset of these pointers.
2 Overview
The program operates on a fixed set of typed objects; the identity of an object is given by its address and its type. (For example, for
each user-defined struct type there is an object of that type for each address properly aligned for objects of that type.) Each object has
a collection of fields determined by its type. A state of the program is a function from objects and field names to values. One field of
each object is a Boolean indicating whether the object is valid ; the valid objects represent those objects that actually exist in a given
state, so object creation/destruction corresponds to object validation/invalidation.
A transition is an ordered pair of states, a prestate and a poststate. Each object has a two-state invariant (a predicate on
transitions); these invariants can mention arbitrary parts of the state, and are mostly generated directly from the annotations on the
program. The invariant of a type/object is the conjunction of all invariants mandated in this manual. An invariant can be interpreted as
an invariant on a single state by applying it to the transition from the state to itself (stuttering transition). A state is good if all object
invariants hold in that state; a transition is good if it satisfies the invariant of each object. A sequence of states (finite or infinite) is good
iff all of its states are good and the transitions between successive states of the sequence are good.
A transition updates an object if some field of the object differs between the prestate and poststate of the transition. A transition is
legal if its prestate is not good or if it satisfies the invariants of all updated objects. A sequence of states is an legal execution iff the
initial state is good and the transition from each nonterminal state of the sequence to its successor is legal. The program is good iff every
legal execution of the program is good; successful verification of the program shows that it is good.
A type is admissible iff, for every object o of the type, (1) every legal transition with a good prestate satisfies the invariant of o,
and (2) the poststate of every good transition from a good state satisfies the invariant of o. It is easy to prove by induction on legal
executions that if all object types are admissible, the program is good. The program is verified by proving that every type of the program
is admissible. (There is a type corresponding to each function; admissibility if this type shows that changing the state of the system
according to the operational semantics of the function is legal.)
Each valid object has a Boolean ghost field that says whether it is closed, and a ghost field that gives its owner (which is also an
object). User-defined object invariants are guaranteed to hold only when the object is closed. Threads are also modelled as objects; in
the context of a thread, an object owned by the thread is said to be wrapped if it is closed, and mutable if it is open (not closed). Only
threads can own open objects. The owner of an open object has “exclusive” use of the object, and so can operate on it sequentially. An
implicit invariant is that nonvolatile fields of objects don’t change while the object is closed, so such fields can also be read sequentially if
the object is known to be closed. Fields of closed objects can be updated only if they are marked as volatile; such fields can be accessed
only within explicitly marked atomic actions.
Each object field is either concrete or ghost; concrete fields correspond to data present in a running program. Each concrete field
of each object has a fixed address and size. Each object has an invariant saying that concrete fields of valid objects don’t overlap, and
verification of a function is that it accesses only fields of valid objects; thus, every legal execution of good program is simulated by a
legal execution in which concrete field accesses are replaced by memory accesses to shared C heap. The program can include ghost code
not included in the unannotated program; however, verification guarantees that all such code terminates, and its execution does not
change the concrete state. This implies that every legal execution of the unannotated program is the projection of a legal execution of
the program, which allows properties of the program to be projected to properties of the unannotated program.
Each thread has a field that gives its “local copy” of the global state. When a thread updates an object, it also updates the local copy;
when it reads an object, it reads from the local copy. Just before each atomic update, the thread updates its local copy to the global
state. It is an invariant of each thread that for any object that it owns, the local copy agrees with the actual object on all fields if the
object is open and on all nonvolatile fields if the object is closed. However, assertions that mention objects not directly readable by the
thread (without using an atomic action) might reference fields where the local and global copies disagree; thus, assertions that appear in
the annotation of a thread are guaranteed to correspond to global assertions only at the beginning of an atomic action. This machinery
allows us to “pretend” that threads are interrupted by other threads only just before entering explicit atomic actions.
3 Preprocessing
The program must #include ; this inclusion must precede any annotations (after expansion of #include directives).
VCC reserves (in both the program and the unannotated program) the preprocessor macro names VERIFY1, _VCC_H, and the macro
_(...)2. All VCC annotations occur within this macro. If VERIFY is not set, _() is defined as whitespace, resulting in the unannotated
program. VCC assumes that the unannotated program is a legal C program, i.e. one that a conformant C compiler would accept.
VCC uses the C preprocessor, so comments and macro expansion follow the rules of C. Preprocessor commands are permitted inside
of annotations.
4 Syntax
VCC reserves identifiers starting with \, using them as function names, field names, or operators.
VCC adds the following infix operators. Each has the given associativity. The specified Unicode characters can also be used.
operator unicode associativity description
==>
<==
<==>
∈
\in
\is
\inter ∩
\union ∪
\diff
\subset ⊆
right
left
left
left
left
left
left
left
left
implies
explies
iff (if and only if)
set membership
type test
set intersection
set union
set difference
subset
The precedence of operators, in relation to standard C operators in show below:
/ * %
+ -
<< >>
<= => < > \is \inter
\diff
\union
\in
== !=
&
ˆ
|
&&
||
<==
==>
<==>
?:
= += *= etc.
1 The explicit use of #ifdef VERIFY is deprecated.
2 Caveat: VCC currently makes use of a number of other preprocessor macro names, all of which are defined in in the VCC inclusion directory.
This should be fixed.
In addition, there is an additional syntactic productions for expressions:
::= ;
::= \forall | \exists | \lambda
::= |
::= {}
The scope of the variables declared in the declarators in the first production extends to the end of the expression. The unicode characters
λ, ∀, and ∃ can be used as well, in place of \lambda, \forall, and \exists respectively.
The syntax of types is extended with the type constructions defined in section 5.
4.1 Annotations
VCC annotations are of the form _(tag stuff), where tag is a annotation tag and stuff has balanced parentheses (after preprocess-
ing). Each VCC annotation is described here with an entry of the form: _(tag args) (class)
where args is a sequence of 0 or more parameter declarations (including types) and “class” describes the syntactic role of the annotation,
which is one of the following:
statement an annotation that acts syntactically as a statement;
cast an annotation that acts syntactically as a (type) cast in expressions (in concrete or ghost code);
contract an annotation that appears either between a function declaration and the following body or semicolon, or between a loop
construct and the body of the loop; of a function or a block (in concrete or ghost code);
specifier an annotation that appears in the syntactic role of a function specifier (just before a function declaration or definition);
compound an annotation that can appear only in the annotation of a compound type definition, just before the struct or union
keyword;
special an annotation whose role is described in the text.
Several VCC annotations allow a variable number of arguments of the same type. In such cases, we write the argument as a single typed
argument followed by an ellipsis; the actual parameters are to be comma separated iff the ellipsis is preceded by a comma.
In addition to annotations, VCC also provides a number of additional types and functions that can be used inside of annotations.
These types and functions all have names starting with \. Their syntax is given using conventional C declarations.
Certain annotations create a pure context where state changes are not permitted, certain constructs are not allowed, and type promo-
tions are somewhat different. Such contexts are marked :pure in this manual; this keyword does not apepar in annotations.
Certain annotations, constants, and functions can appear only in inside of certain contexts:
pure can appear only in a pure context;
thread can appear only within the body of a function declaration;
member can only appear in the syntactic position of a member declaration of a compound data type;
invariant can only appear inside an _(invariant) annotation inside the declaration of a compound type definition.
5 Types
A type is said to be concrete if it is a type of the unannotated program, and is otherwise said to be ghost. Each type is classified by the
number of possible values of that type, which is either finite, small (countable), or large (equinumerous with the reals). Concrete types
are all finite; for each kind of ghost type defined below, we give the class of that type. The class of a struct or union type is the class
of its largest member (including ghost fields), so while a C compound type without ghost fields is finite, one with ghost fields might be
small or large. The class of an array type is the class of its base type.
All types can be classified as either value types or object types. Object types are compound types (i.e., struct or union types),
array object types, \threads, \claims, and \blobs. All other types are value types. The objects of a program are of object types, while
fields of objects are of value types.
5.1 Integral Types
\bool (finite)
The Boolean types, with values \true and \false. These values are equal to the \natural numbers 0 and 1, respectively.
\natural (small)
The type of (unbounded) natural numbers.
\integer (small)
Mathematical (unbounded) integers.
C integral types can be cast to \integer, or unsigned integral types cast to \natural, in the obvious way. When a signed value is
cast to \natural in an impure context, there is an implicit assertion that the value cast is nonnegative. In a pure context, the casting of
a negative value to a \natural is equivalent to applying some unknown (but fixed) function from integer to natural. In any context,
casting any integral type to \bool yields \true if the argument is equal to 0 and \false otherwise.
The C arithmetic operators are extended to the types \natural and \integer with the obvious interpretation3.
An arithmetic operator instance is said to occur in an \unchecked context if it is is a subterm of an expression marked _(unchecked);
otherwise, it is said to be checked. On any checked arithmetic operation, VCC asserts that the operation does not overflow or underflow4.
On any checked division, VCC asserts that the divisor is nonzero. On any checked cast between arithmetic types, VCC asserts that the
cast value fits in the range of the target arithmetic type5. The result of an expression of arithmetic type is implicitly cast to \integer if
(1) the context is pure and checked, or (2) it is subject to a binary arithmetic operator and the other operand is \natural or \integer.
5.2 Record Types
_(record)
A record is like a C struct or union, except that it is treated as a single abstract value. Record types are declared using the same syntax
as the declaration of a struct type, but with the following differences:
• The keyword struct is immediately followed by _(record).
• The fields of a record type cannot be marked as volatile.
• Record types have no invariants.
• Fields of a record cannot be of struct types or array types (but can be of map type or record type).
• If a field of a record is of union type, it must have a _(backing_member).
If T is a record type, the expression (struct T) produces an arbitrary value of type T.
If e is an expression of record type with fields f1,f2,..., and e1,e2,... are expressions that are assignment compatible with the
types of fields f1,f2,... respectively, then
e / { .f1 = e1, .f2 = e2, ...}
is equal to the record e with the fields f1,f2,... set to the values e1,e2,... respectively.
If v is a variable of a record type with a field f, then v.f = e translates to v = v / {.f = e}; if v.f is itself a record with field
g, then v.f.g = e translates to v = v / {.f = v.f / {.g = e}}, and so on.
_(record T { ... }) (macro)
Expands to _(ghost typedef struct _(record)T { ... } T)
5.3 Map Types
T1[T2]
The type of maps (i.e., mathematical functions) from type T2 to type T1. T1 and T2 must be value types, and T2 must not be a large
type. If T2 is finite, this has the same class as T1. If T2 is small, the resulting type is large.
Map types can also appear in declarations and typedefs, and there the syntax matches the syntax of C arrays, except that a type
appears in between the array brackets instead of a size.
\lambda T v; :pure e (expression)
Here, the scope of v continues to the end of e; it introduces v as a variable of type T. If T1 is the type of e, this expression has type
T1[T]; the resulting value maps each v to the corresponding value of e, as evaluated in the current state.
If e is a map of type T1[T2] and x is a value of type T2, then e[x] is an expression of type T1, whose value is given by the value
of e at the point x. If v is a lvalue of type T1[T2] and e1 is an expression of type T2, then the expression v[e] = e1 is equivalent to the
assignment v = (\lambda T2 u; (u == e)? e1 : v[u]) where u is a fresh variable. This is extended to maps of maps in the obvious
way.
3 Caveat: Because of compiler limitations, VCC currently does not allow << or >> operators with the second argument a literal over 63.
4 VCC should not allow unchecked signed overflows or underflows (at least in concrete code), because the C standard specifies these as resulting in undefined
behavior; however currently VCC assumes that these produce some arbitrary but fixed function of the inputs.
5 VCC currently does not support floating point arithmetic, in that it does not know anything about the semantics of various floating point operations, and
does not check for floating point overflow, underflow, or division by zero. However, on platforms where floating point exceptions do not affect control flow,
verification remains sound for programs that uses floats or doubles.
5.4 Inductive Types
An inductive datatype is introduced by a top-level annotation
_(datatype T {
case c1();
case c2();
...
})
where is a comma-separated list, each element of which is a type name optionally followed by a parameter name. This declares
each ctor to be a constructor of values of type T. Types can be mutually recursive, but a type cannot be referenced before being declared.
The form _(type T) declares T as an abstract type, which can (but doesn’t have to) be later redefined as a record or datatype.
The ==, !=, and = operators are extended to T, but it is an error to apply them to compare an argument of type T and an argu-
ment of another type, or to assign between such mismatched types.
The C switch statement is extended to inductive types as follows: if v is an expression of type, VCC allows the program statement
switch (v) {
case c1(t11,t12,...): P1;
case c2(t21,t22,...): P2;
...
}
where each tij is a variable name not in scope, no name occurs as more than one of the tijs, each constructor of type T occurs exactly
once among T1, T2, ..., and each of the cases has proper arity for the given constructor. Is is asserted that there is no fallthrough
between cases (i.e., a break or return at the end of each one is mandatory). The switch statement above translates to the following:
{
unsigned x;
switch (x) {
case (1) : {
T11 t11; T12 t12; ...
_(assume v == c1(t11,t12,...))
{ P1 }
break;
} case (2) : {
T21 t21, T22 t22; ...
_(assume v == c2(t21,t22,...))
{ P2 }
break;
} ...
default : { _(assume \false) }
}
}
5.5 Pointers
\object (type) (small)
The type of pointers.
ˆT (small)
The type of pointers to ghost objects of type T. (T can be a concrete or ghost type.)
The program determines a fixed set of pointers. Pointers to instaces of object types are called object pointers; pointers to instances of
value types are called value pointers. We typically identify an object and the (unique) pointer that points to it, and so when we talk
about an object o, o is really an object pointer.
A pointer is characterized by the following (state-independent) parameters:
\natural \addr(\object p)
The address of p. If !\ghost(p), \addr(p)+ \sizeof_object(p)< UINT_PTR_MAX.
\type \typeof(\object p)
The type of p. In C terms, this can be thought of as the type of object to which p points.
\bool \ghost(p)
True if p is a ghost pointer (i.e., points to the ghost heap). If not, we say p is concrete.
\non_primitive_ptr(\object p)
True if p is an object.
\object \embedding(\object p)
The object of which p is a part of. If p is an object, the result is undefined. If p is a concrete value pointer, \embedding(p) is concrete.
When the & operator is applied to an expression of the form o->f, where f is of value type, the aforementioned object is o. When it is
applied to a local variable, it is the object containing the variable.
size_t \sizeof_object(\object p)
Equivalent to \sizeof(T), where T is the type of *p. This depends only on \typeof(p).
In a pure context, for pointers p and q, p == q iff p and q agree on all the parameters above.
Every pointer of the program has a footprint (a set of addresses) defined as follows. If p is a concrete value pointer, its footprint is
the set of addresses [\addr(p),\addr(p)+ \sizeof_object(p)). If p is an object, its footprint is the union of the footprints of all
concrete value pointers q such that \embedding(q)== p. Footprints of distinct concrete value pointers with the same embedding are
disjoint. If p is a concrete object, its concrete footprint is a subset of [\addr(p),\addr(p)+ \sizeof_object(p)).
p \is T (expr)6
p must be a pointer, and T a value type. This is equivalent to (p == (T *)p)|| (p == (T ˆ)p).
_(retype) (cast)
The argument to this case must be a value pointer p. If there is a \valid object o with a field f such that &o->f and p point have the
same base type and the same address, then this operator returns &o->f. Otherwise, the result of the operation is undefined. This opera-
tor is typically used when p points to a value field of struct that is a member of a union, and some other union member is currently \valid.
VCC does not allow C’s silent promotion of an expression of type (void *) to another pointer type; such a promotion requires an
explicit cast7.
5.5.1 Pointer Sets
typedef \bool \objset[\object];
\objset is the type of sets of pointers. While the definition above will be its eventual semantics, it is currently treated as a distinct type
(because it is triggerred differently from other maps).
_(pure)\bool \in(\object o, \objset s) (infix operator)
_(ensures \result <==> s[o])8
_(pure)\objset +(\objset s, \object o) (infix operator)
_(ensures \forall \object o1; o1 \in \result <==> o1 == o || o1 \in s)
_(pure)\objset -(\objset s, \object o) (infix operator)
_(ensures \forall \object o1; o1 \in \result <==> o1 != o && o1 \in s)
(+= and -= are extended analogously.)
_(pure)\objset \universe()
_(ensures \forall \object o; o \in \result)
_(pure)\objset \everything()
_(ensures \result == \universe())
_(pure)\bool \disjoint(\objset o1, \objset o2)) (infix operator)
_(ensures \result <==> \forall \object o; !(o \in s1)|| !(o \in s2))
_(pure)\bool \subset(\objset s1, \objset s2) (infix operator)
_(ensures \result <==> \forall \object o; o \in s1 ==> o \in s2)
_(pure)\objset \diff(\objset s1, \objset s2) (infix operator)
_(ensures \forall \object o; o \in \result <==> o \in s1 && !(o \in s2))
_(pure)\objset \inter(\objset s1, \objset s2) (infix operator)
_(ensures \forall \object o; o \in \result <==> o \in s1 || o \in s2)
6Deprecated
7This is justified on the grounds that it avoids potential errors without changing the compiled code.
8 Caveat: this is not its actual definition, for type reasons, but conveys the meaning.
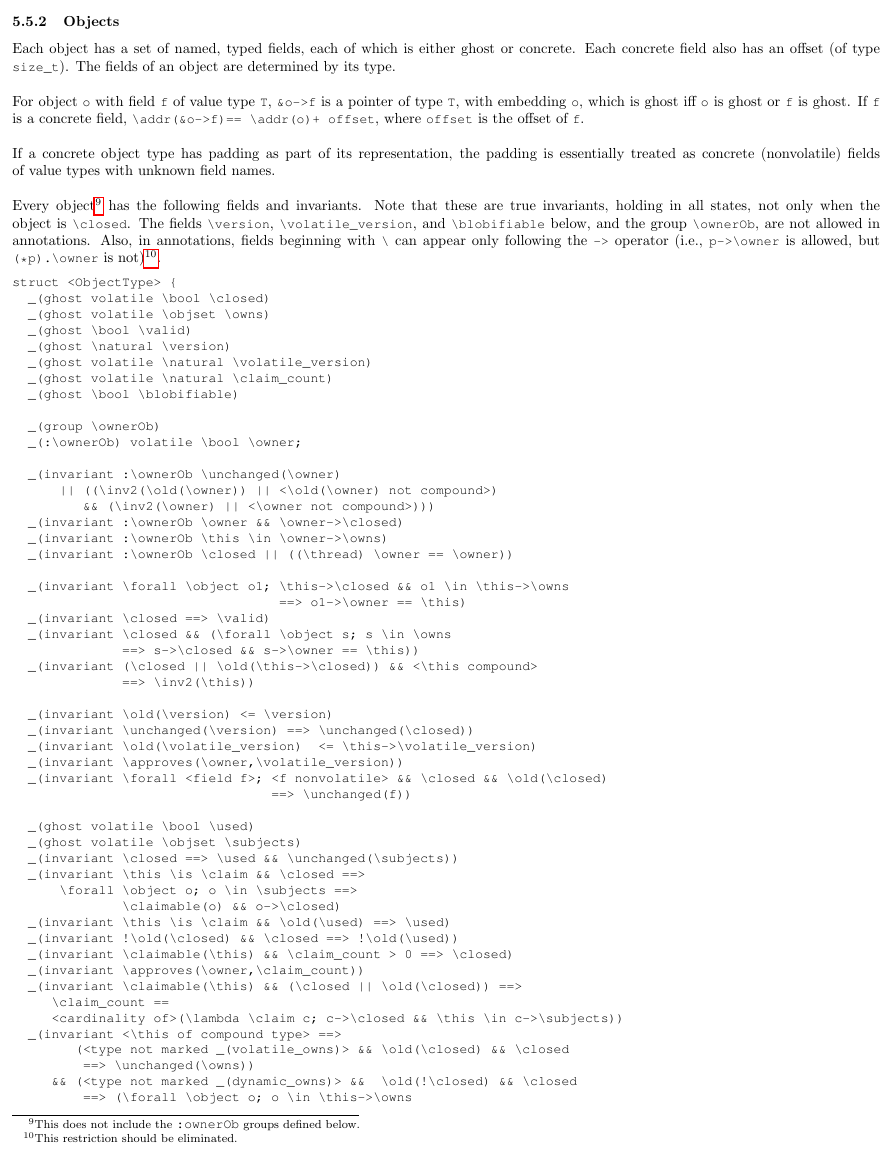
5.5.2 Objects
Each object has a set of named, typed fields, each of which is either ghost or concrete. Each concrete field also has an offset (of type
size_t). The fields of an object are determined by its type.
For object o with field f of value type T, &o->f is a pointer of type T, with embedding o, which is ghost iff o is ghost or f is ghost. If f
is a concrete field, \addr(&o->f)== \addr(o)+ offset, where offset is the offset of f.
If a concrete object type has padding as part of its representation, the padding is essentially treated as concrete (nonvolatile) fields
of value types with unknown field names.
Every object9 has the following fields and invariants. Note that these are true invariants, holding in all states, not only when the
object is \closed. The fields \version, \volatile_version, and \blobifiable below, and the group \ownerOb, are not allowed in
annotations. Also, in annotations, fields beginning with \ can appear only following the -> operator (i.e., p->\owner is allowed, but
(*p).\owner is not)10.
struct {
_(ghost volatile \bool \closed)
_(ghost volatile \objset \owns)
_(ghost \bool \valid)
_(ghost \natural \version)
_(ghost volatile \natural \volatile_version)
_(ghost volatile \natural \claim_count)
_(ghost \bool \blobifiable)
_(group \ownerOb)
_(:\ownerOb) volatile \bool \owner;
_(invariant :\ownerOb \unchanged(\owner)
|| ((\inv2(\old(\owner)) || <\old(\owner) not compound>)
&& (\inv2(\owner) || <\owner not compound>)))
_(invariant :\ownerOb \owner && \owner->\closed)
_(invariant :\ownerOb \this \in \owner->\owns)
_(invariant :\ownerOb \closed || ((\thread) \owner == \owner))
_(invariant \forall \object o1; \this->\closed && o1 \in \this->\owns
_(invariant \closed ==> \valid)
_(invariant \closed && (\forall \object s; s \in \owns
==> s->\closed && s->\owner == \this))
_(invariant (\closed || \old(\this->\closed)) && <\this compound>
==> o1->\owner == \this)
==> \inv2(\this))
_(invariant \old(\version) <= \version)
_(invariant \unchanged(\version) ==> \unchanged(\closed))
_(invariant \old(\volatile_version)
_(invariant \approves(\owner,\volatile_version))
_(invariant \forall ; && \closed && \old(\closed)
<= \this->\volatile_version)
==> \unchanged(f))
_(ghost volatile \bool \used)
_(ghost volatile \objset \subjects)
_(invariant \closed ==> \used && \unchanged(\subjects))
_(invariant \this \is \claim && \closed ==>
\forall \object o; o \in \subjects ==>
\claimable(o) && o->\closed)
_(invariant \this \is \claim && \old(\used) ==> \used)
_(invariant !\old(\closed) && \closed ==> !\old(\used))
_(invariant \claimable(\this) && \claim_count > 0 ==> \closed)
_(invariant \approves(\owner,\claim_count))
_(invariant \claimable(\this) && (\closed || \old(\closed)) ==>
\claim_count ==
(\lambda \claim c; c->\closed && \this \in c->\subjects))
_(invariant <\this of compound type> ==>
( && \old(\closed) && \closed
==> \unchanged(\owns))
&& ( &&
\old(!\closed) && \closed
==> (\forall \object o; o \in \this->\owns
9This does not include the :ownerOb groups defined below.
10This restriction should be eliminated.
<==> )
&& (\forall ;
(<\approves(\this->\owner,f) is a top-level conjunct
of an invariant of this type>
==> \unchanged(\volatile_version) || !\closed(\this)
|| \unchanged(f))))
_(invariant \old(\valid) && \valid ==> \unchanged(\blobifiable))
}
5.6 Special Forms in Invariants
\bool \wrapped(\object o) (thread)
_(ensures \result <==> o->\owner == \me && o->\closed)
_(dynamic_owns) (compound)
_(volatile_owns) (compound)
These cannot both appear on the same type definition. See the invariants above and the definition of _(wrap) for their meaning.
\bool \mine(\object o1) (invariant)
_(ensures \result <==> o1 \in \this->\owns)
If the object type is not marked _(dynamic_owns) or _(volatile_owns), this function can only be used as the outermost function
of a top-level conjunct of an invariant.
\bool \approves(\object o, f )) (special)
This function can appear only as a top-level conjunct of an object invariant of a type T, f must be a field of T, and o must be a field of T or
the expression \this->\owner. If o is a field other than \owner, \approves(o,o) must also be a top-level conjunt of an invariant of T.
\approves(o,f) translates to \unchanged(f)|| !o || \inv2(f)|| ( && !\unchanged(\volatile_version)).
5.7 States
\state (large)
The type of states.
T \at(\state s, T e)
The evaluation of expression e in the state s (with all free variables replaced with their value in the current state).
When \at occurs (implicitly or explicitly) in the declaration of a function, purely local variables are implicitly replaced with their
actual values at the state in which the form is evaluated. (For function preconditions and postconditions, this state is function entry.)
\state \now()
The current state.
\bool \unchanged(\object o)
For value pointer o, this translates to *o == \old(*o) For object o, this holds iff, for every field f of o, \unchanged(o->f).
5.7.1 Threads
\thread (small)
The type of threads.
const \thread \me (thread11)
This is a pure local variable that gives the current thread.
5.8 Compound Types
5.8.1 Ghost Fields
Within a compound type, a field is ghost is it occurs inside the scope of a _(ghost) annotation. Ghost fields may be of any concrete or
ghost type.
In annotations of a compound type, the scope of a member name includes the entire type definition.
11Caveat: currently, VCC does not check this, and should be fixed.
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
