logo资料库

省二等奖2019全国大学生数学建模a.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：1.04M 资料格式：pdf 举报 版权申诉
第1页 / 共32页
第2页 / 共32页
第3页 / 共32页
第4页 / 共32页
第5页 / 共32页
第6页 / 共32页
第7页 / 共32页
第8页 / 共32页
资料共32页，剩余部分请下载后查看
    高压油管的压力控制 摘 要 高压油管是燃油发动机的主要组成部分, 通过对燃油机高压油管内部的压 力控制, 可以提高燃油发动机的工作效率。本文根据题目给出的数据及我们搜集 的资料, 基于柴油机泵-管-嘴式喷油系统的几何结构及工作原理, 建立了高压 油管喷油 与供 油 的微分方程模型 , 利用积 分法 , 分离变 量法及图 解法结合 MATLAB 软件对该模型进行求解回答了题目提出的所的问题。 针对问题一, 首先对喷油系统的工作原理及高压油管的几何结构进行分 析, 并对题目附件 3 给出的压力与弹性模量的数据进行二次拟合, 得到两者 间的函数关系式；其次，据上述关系并结合搜集到的文献资料建立了微分方程模 型, 求解得到燃油压力与密度的关系, 从而建立了供油与喷油模型；最后，利 用 MATLAB 软件对上术模型进行求解, 得出:要将高压油管内的压力尽可能稳定 左右,需要把单向阀每次开启的时长设置为 1.9251ms.要想在分别经 在 100 过约 2 s, 5s, 10s 的调整过程后稳定在 150 ,单向阀开启的时长分别应 设置为 66.2ms, 32.1ms, 与第一阶段 13.1ms 第二阶段 22.12ms。 针对问题二,此题是在问题一的基础上加入了凸轮与柱塞腔的工作系统以及 针阀对喷油嘴的控制, 根据题中给出的附件 1 及附件 2 并结合查找的文献资料, 对凸轮, 针阀的工作原理进行分析得到喷油与供油量, 利用积分法以及图解 法, 结合问题一中得出的模型, 再利用 MATLAB 进行求解, 得出:凸轮角速度 为 。 针 对 问题 三 , 此题 首先 是 在问 题二 的基础 上 增加 了一 个针 阀式 喷 油 器, 利用问题二的求解方法, 用 MATLAB 求解得出具体喷油和供油策略为:供 油方面让凸轮一直以 的角速度进行运作。对于喷油, 先开启其中 任意一个针阀式喷油器进行喷油工作, 直到时间过去 50ms 后,开启另外一个针 阀式喷油器进行喷油工作,如此交替进行,循环往复。对于增加了单向减压阀的情 况, 对之前得出的喷油器所需喷油的次数为小数的问题进行进一步分析, 结 合问题一所得公式与模型, 利用 MATLAB 进行求解,得出高压油泵和减压阀的控 制方案具体如下:在供油方面, 让凸轮以 的角速度进行工作, 喷 油策略采取与上题相同的交替喷油方式。对于减压阀, 我们设定当时间走过供 油的半个周期(200ms)时, 开启单向减压阀 0.3217ms, 如此循环往复。 关键词:高压油管，压力控制，微分方程模型，二次拟合，积分法，图解法 aMPaMP7.0631/rads14.1263/rads15.708/rads
    一、问题的背景和重述 现有一高压燃油系统, 燃油经过高压油泵从 A 处进入高压油管, 再由喷口 B 喷出。燃油进入和喷出的间歇性工作过程会导致高压油管内压力的变化, 使得所 喷出的燃油量出现偏差, 从而影响发动机的工作效率。现有以下问题: 问题 1。存在一高压油管, 已知高压油泵和喷油器工作方式及其规格, 要求 解决以下两个问题: (1)如何控制高压油泵单向阀的单次开启时间, 将高压油管内的压力尽可能 稳定在 100 左右。 (2)如果要将高压油管内的压力从 100 增加到 150 , 且分别经过 约 2 s、5 s 和 10 s 的调整过程后稳定在 150 , 单向阀开启的时长 应如何调整？ 问题2。 在问题一的基础上, 在高压油泵中增加了凸轮与柱塞腔的工作系统, 以及针阀对喷油嘴的控制。已知凸轮边缘曲线与角度的关系, 以及一个喷油周期 内针阀升程与时间的关系。在柱塞腔内的压力大于高压油管内的压力时, 柱塞腔 才能单向阀开启, 和针阀的运动有固定提升高度以及周期的条件下, 要求确定 凸轮的角速度, 使得高压油管内的压力尽量稳定在100 左右。 问题3。在问题2的基础上, 再增加一个喷油嘴, 每个喷嘴喷油规律相同, 为 了使得高压油管内的压力尽量稳定在100 左右。要求解决以下两个问题: (1)如何调整在该情况下喷油和供油策略。 (2)在此基础上, 在D处安装一个单向减压阀。给出高压油泵和减压阀的控制 方案。 2.1 问题一的分析 二、问题分析 题目要求计算使高压油管稳定在 100 , 以及分别经过三种不同时间后, 稳定在 150 的高压油泵单向阀的单次开启时间, 根据参考文献 喷油系 统的几何结构以及燃油在系统中流动的原理, 关于喷油器的喷油体积，利用题目 中给出了喷油速率与时间的关系图，喷油速率的积分即为一次喷出油的体积。打 开单向阀时，供油入口与高压油管形成一个压力差，利用题目注 2 给出的流量公 式，即可计算出在该压力差下，进入高压油管的流量。再计算喷进的燃油的量与 1 aMPaMPaMPaMPaMPaMPaMPaMP12
    喷出的燃油的量对高压油管压力的影响, 为了使高压油管内的压强稳定在 100 ，只需要使喷油器喷出的油量等于进油端进入的油量即可，利用该关系即 可求出单向阀开启时间。 2.2 问题二的分析 该问题相对于问题一而言，喷油器的喷油方式发生了改变，当针阀的升程大 于 0 时，高压油管内的油则从针阀与封闭座的缝隙中喷出，喷出油的多少则取决 于针阀上升的高度，针阀的升程越大，针阀与封闭座的缝隙越大，即喷油的面积 越大，该面积等于封闭座的横截面积减去针阀的底面积，所以将该面积带入到注 2 的流量公式中，即可求喷油器出喷油速率。进油端则由凸轮驱动柱塞上下运动 提供油，所以进油的多少则取决于凸轮的角速，在单向阀打开之前，柱塞腔内的 油量不发生改变，因此柱塞腔内的压力达到 100 之前可利用柱塞腔内油的质 量不变计算出临界条件时，柱塞腔内剩余的容积，压力达到 100 之后则是将 该容积压缩为 20 ，这就可以计算出一次向高压油管内注入的油量。只需要 使喷油器喷出的油量等于进油端进入的油量即可，利用该关系即可求出凸轮的角 速度。 2.3 问题三的分析 此题首先是在问题二的基础上增加了一个针阀式喷油器, 因增加的喷油嘴 与原来的喷油嘴规律相同，所以就相当于将喷油速度变成原来的两倍， 利用问 题二的求解方法即可求出满足条件的凸轮角速度, 对于增加了单向减压阀的情 况, 对之前得出的喷油器所需喷油的次数为小数的问题进行进一步分析, 将之 取整以计算调整后的凸轮角速度, 再将在此过程中因对喷油次数的取整而产生 残留燃油量作为单向减压阀所需排出的燃油量, 代入问题一所得公式即可求出 单向减压阀所需开启时间。 三、模型的假设 1. 假设温度对高压油管内的压力没有影响。 2. 假设机器性能良好, 系统不会出现故障。 3. 假设燃油物理性质的变化对压力波的传递没有影响。 4. 假设燃油的密度只与压力有关。 5. 假设凸轮转速稳定, 不受惯性影响。 6. 假设喷油嘴外侧的压强为一个标准大气压。 2 aMPaMPaMP3mm
    四、符号说明 符号 意义 单位 符号 意义 单位 高压油管内的压力 单位时间流入高压 油管气体的体积 高压侧燃油的密度 弹性模量 高压油管的内腔体 积 高压油管的内腔直 径 高压油管的内腔长 度 当柱塞腔内的压力 达到单向阀开启要 求时, 柱塞腔中的 残余体积。 小孔的面积 管内压力 100 时, 单次喷出燃油 后, 压力的变化量 管内压力 150 时, 单次喷出燃油 后, 压力的变化量 总需开启单向阀的时 间 一个周期内需要开启 单向阀的时间 使管内压力稳定 150 的单向阀应开启 的时间 柱塞腔的高度 柱塞运动到下止点 时, 柱塞腔的总容积 凸轮式高压油泵仅完 成一次供油后, 高压 油管内增加的压力 仅由针阀式喷油器一 次喷出燃油体积 3 PaMPP出1aMPaMPV进3mmP出2aMPaMP3/mgmmt总msEaMPt开msV管3mmt稳aMPmsdmmh柱mmhmmV柱3mmV临3mmP加aMPA2mmV喷3mm
    一个周期内高压油 管内的瞬时压力 高压油管的稳定压 力 高压油管一瞬间减 少的压力 柱塞腔内直径 柱塞运动到上止点 时, 柱塞腔残余容 积 低压燃油的密度 压力为 100 时, 燃油的密度 流量系数 无 仅由针阀式喷油器工 作一次高压油管内减 少的压力 凸轮转动一周所需时 间 凸轮角速度 单向减压阀需要喷出 燃油的量 单向减压阀需要喷出 燃油的体积 燃油通过单向减压阀 的流量 单向减压阀开启一次 所需的时间 五、模型的建立与求解 5.1 问题一的模型建立与求解 针对本题, 将系统的工作过程分成仅供油与仅喷油两个过程并分别建立模 型, 最后把得到模型与题目所给的信息结合进行求解。 5.1.1 供油模型建立 通过查阅资料 , 得到理想气体状态方程: 4 P管aMPP减aMP1PaMPT轮sP出aMP/radsd柱mmP排aMPV残3mmV排3mm低3/mgmmQ排3/mmms高aMP3/mgmmt排msC3=PVnRT物
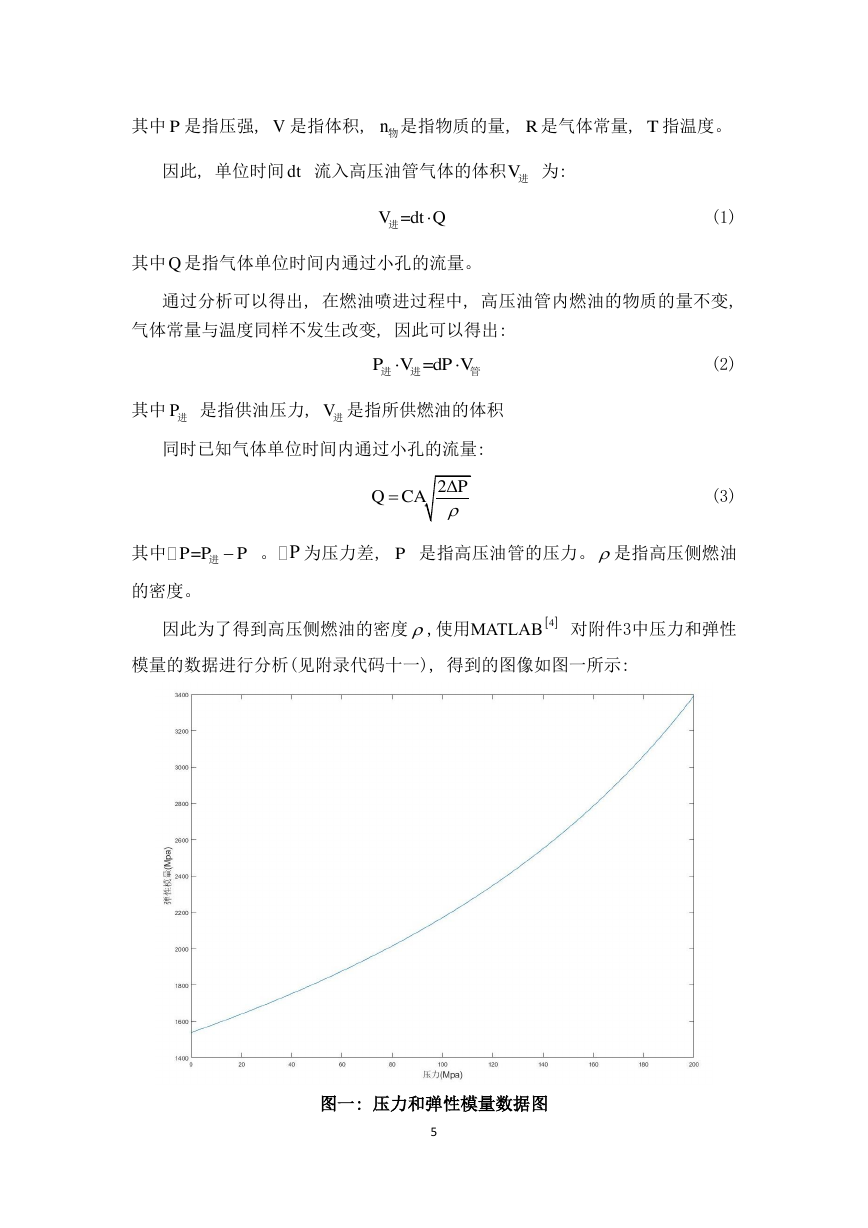
    其中 是指压强, 是指体积, 是指物质的量, 是气体常量, 指温度。 因此, 单位时间 流入高压油管气体的体积 为: (1) 其中 是指气体单位时间内通过小孔的流量。 通过分析可以得出, 在燃油喷进过程中, 高压油管内燃油的物质的量不变, 气体常量与温度同样不发生改变, 因此可以得出: (2) 其中 是指供油压力, 是指所供燃油的体积 同时已知气体单位时间内通过小孔的流量: (3) 其中 。 为压力差, 是指高压油管的压力。 是指高压侧燃油 的密度。 因此为了得到高压侧燃油的密度 ,使用MATLAB 对附件3中压力和弹性 模量的数据进行分析(见附录代码十一), 得到的图像如图一所示: 图一: 压力和弹性模量数据图 5 PVn物RTdtV进=VdtQ进Q=PVdPV进进管P进V进2ΔPQCA==PPP−进PP4
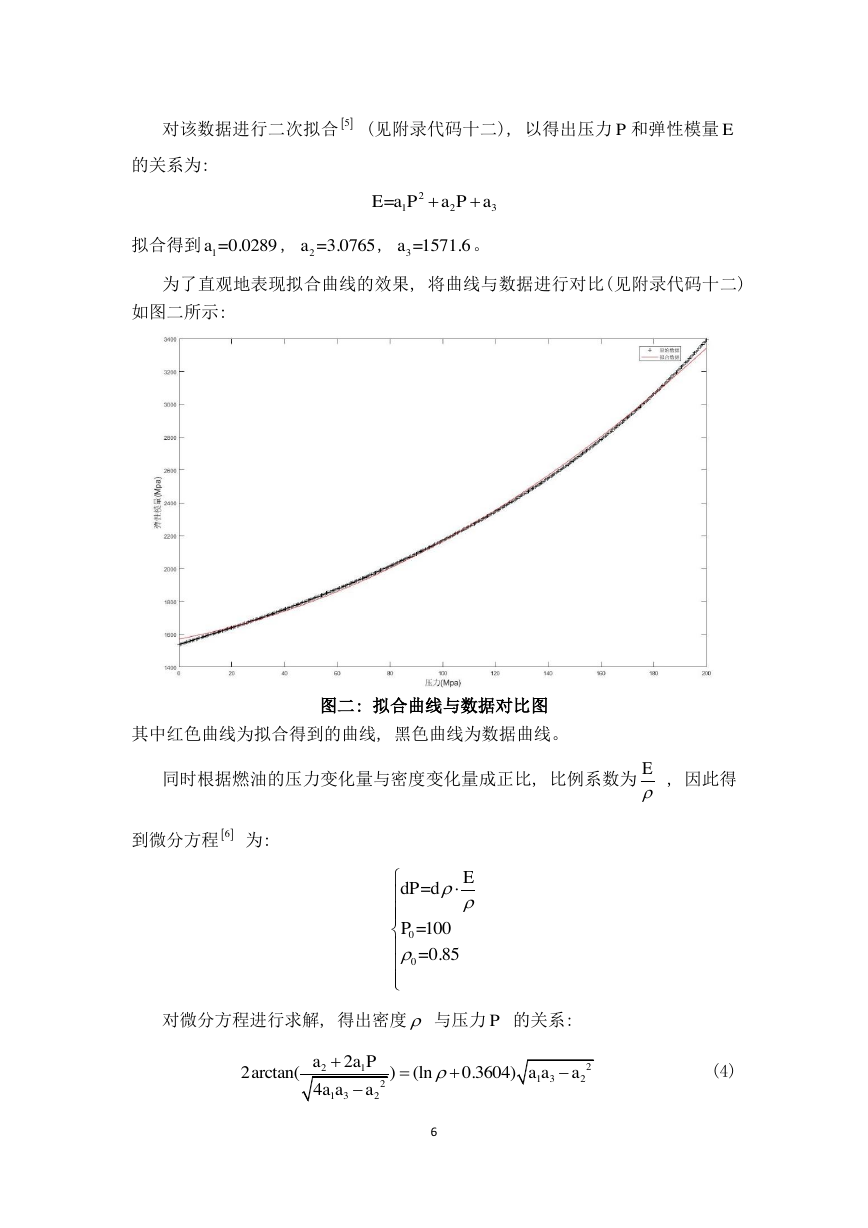
    对该数据进行二次拟合 (见附录代码十二), 以得出压力 和弹性模量 的关系为: 拟合得到 , , 。 为了直观地表现拟合曲线的效果, 将曲线与数据进行对比(见附录代码十二) 如图二所示: 其中红色曲线为拟合得到的曲线, 黑色曲线为数据曲线。 图二: 拟合曲线与数据对比图 同时根据燃油的压力变化量与密度变化量成正比, 比例系数为 , 因此得 到微分方程 为: 对微分方程进行求解, 得出密度 与压力 的关系: (4) 6 5PE2123=EaPaPa++1=0.0289a2=3.0765a3=1571.6aE600==100=0.85EdPdPP221132213222arctan()(ln0.3604)4aaPaaaaaa+=+−−
    联立式(1)(2)(3)(4),可以得出供油模型: 其中 为高压油管的稳定压力, 为初始时间。 5.1.2 喷油模型建立 现在考虑没有燃油喷进, 仅有燃油喷出的情况下, 管内压力 的变化情况。 首先将题中已给出的喷油速率示意图转换成函数为: 同样分析可以得出, 在燃油喷出过程中, 高压油管内燃油的物质的量不变, 气体常量与温度同样不发生改变, 因此可以得到喷油模型: (5) 其中 是指一瞬间高压油管中减少的压力。 5.1.3 问题一的求解 对供油模型进行求解并化简, 得出在没有燃油喷出, 仅有燃油喷进的情况 下单向阀 开启时间 与管内压力 的关系为: (6) 由于喷出燃油时, 单次喷出燃油的量较小, 导致高压油管内的压力变化很 小。所以可以忽略在喷出燃油对高压油管内压力的变化的影响。 为了方便计算, 直接将式(5)中 定为 100 。 对出油模型求解, 得到没有燃油喷进, 仅有燃油喷出的情况下, 管内压力 与时间 的关系: 为了计算满足题中要求的单向阀应开启的时间, 首先需要计算单次喷出燃 油后, 压力的变化量 为: 7 102()=1000PPCAdtdPVPtP−==进管进1P0tP10000.2200.22.21002402.22.4ttQttt=−+=PQdtdpV出管P出7tP2392=160-0.5576(-10.3732+)78125PtPaMPPtPPQdtV=出管1P出
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料