2022年山东滨州中考数学试题及答案.doc-资料库

第1页 / 共21页

第2页 / 共21页

第3页 / 共21页

第4页 / 共21页

第5页 / 共21页

第6页 / 共21页

第7页 / 共21页

第8页 / 共21页

2022 年山东滨州中考数学试题及答案温馨提示： 1.本试卷分第Ⅰ卷和第Ⅱ卷两部分，共 4 页．满分 120 分．考试用时 120 分钟．考试结束后，将试题卷和答题卡一并交回． 2.答卷前，考生务必用 0.5 毫米黑色签字笔将自己的姓名、准考证号，座号填写在试题卷和答题卡规定的位置上． 3.第Ⅰ卷每小题选出答案后，用 2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其它答案标号．答案不能答在试题卷上． 4.第Ⅱ卷必须用 0.5 毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液，胶带纸，修正带．不按以上要求作答的答案无效．第Ⅰ卷（选择题共 36 分）一、选择题：本大题共 12 个小题，在每小题的四个选项中只有一个是正确的，请把正确的选项选出来，用 2B铅笔把答题卡上对应题目的答案标号涂黑．每小题涂对得 3 分，满分 36 分． 1. 某市冬季中的一天，中午 12 时的气温是 3 ℃，经过 6 小时气温下降了 7℃，那么当天 18 时的气温是（ A. 10℃ 【答案】B C. 4℃ 10 ℃ 4 ℃ D. ） B. 【解析】【分析】根据有理数减法计算 3 7 【详解】解: ∵中午 12 时的气温是 3 ℃，经过 6 小时气温下降了 7℃， ∴当天 18 时的气温是 3 7 故选 B．     ℃即可．     ℃． 10 10 【点睛】本题考查有理数的减法，掌握有理数的减法法则是解题关键． 2. 在物理学中，导体中的电流Ⅰ跟导体两端的电压 U，导体的电阻 R之间有以下关系： UI  R 去分母得 IR U ，那么其变形的依据是（ B. 等式的性质 2 A. 等式的性质 1 ） C. 分式的基本性质 D. 不等式的性质 2 【答案】B 【解析】【分析】根据等式的性质 2 可得答案．

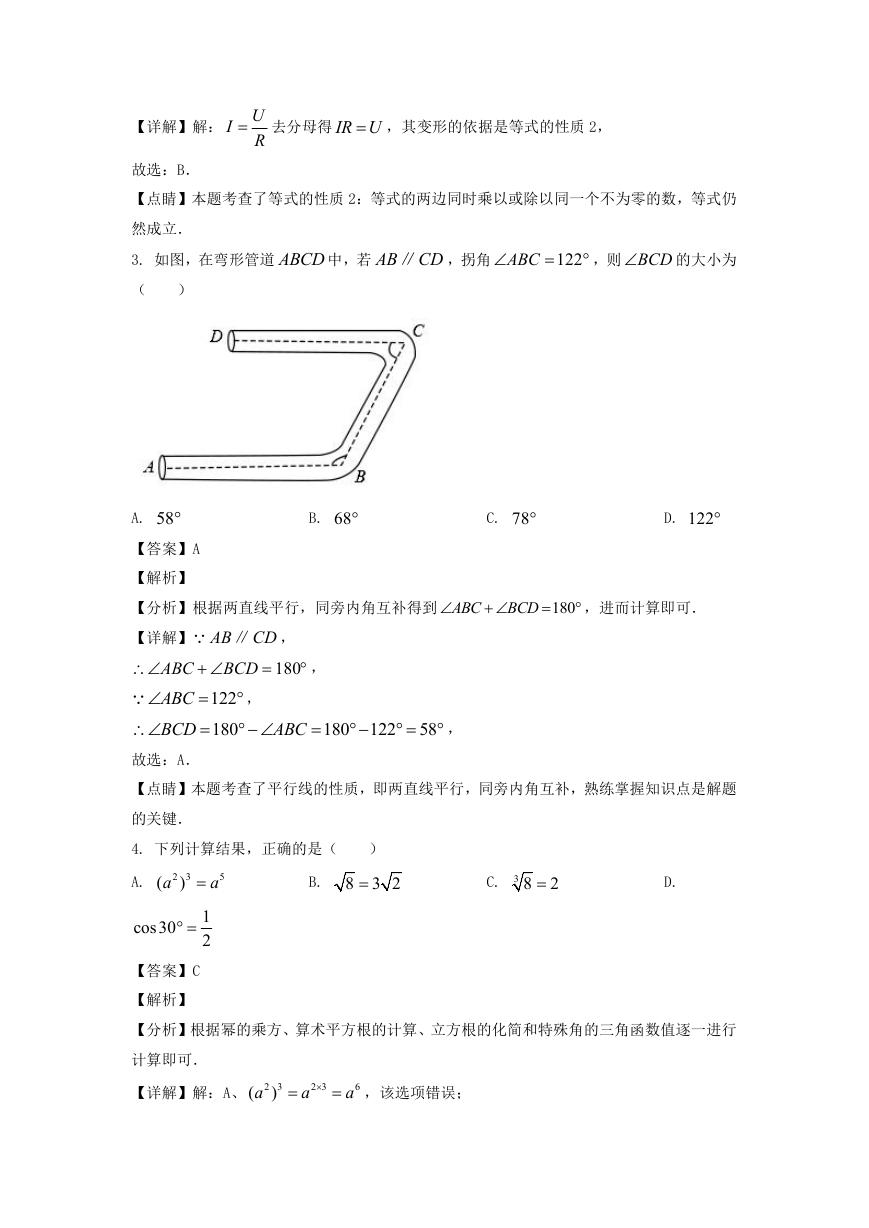
UI  去分母得 IR U ，其变形的依据是等式的性质 2， R 【详解】解：故选：B．【点睛】本题考查了等式的性质 2：等式的两边同时乘以或除以同一个不为零的数，等式仍然成立． 3. 如图，在弯形管道 ABCD 中，若 AB CD∥ ，拐角（） ABC  122  ，则 BCD 的大小为 A. 58 【答案】A 【解析】 B. 68 C. 78 D. 122  ABC   BCD  180  ，进而计算即可．【分析】根据两直线平行，同旁内角互补得到【详解】 AB CD∥     122  180        ， 180 BCD 180   122   ABC  ，， ABC ABC BCD 故选：A．  58  ，【点睛】本题考查了平行线的性质，即两直线平行，同旁内角互补，熟练掌握知识点是解题的关键． 4. 下列计算结果，正确的是（） A. 3 2( )a 5 B. 8  3 2 C. 3 8 2 D. a 1 2 cos30   【答案】C 【解析】【分析】根据幂的乘方、算术平方根的计算、立方根的化简和特殊角的三角函数值逐一进行计算即可．【详解】解：A、 2 3 )a ( 2 3  a 6  ，该选项错误； a

B、 8  2 2 2    2 2 ，该选项错误； C、 3 8  3 2 2 2    ，该选项正确； 2 D、 cos30 ° ，该选项错误； 3 2 故选：C．【点睛】本题考查了幂的乘方、算术平方根的计算、立方根的化简和特殊角的三角函数值，熟练掌握运算法则是解题的关键．    3 3 2 x 1 x  2  x x     5. 把不等式组（） A. C. 【答案】C 【解析】 1 中每个不等式的解集在同一条数轴上表示出来，正确的为 B. D. 【分析】先解不等式组求出解集，再在数轴上表示出来即可．  ②   【详解】 3 2 x ① 1 1 x  2 x     x  3 3 x   ，解①得解②得 5x  ， 不等式组的解集为 3    ，在数轴上表示为： 5x ，故选：C．【点睛】本题考查了解一元一次不等式组及在数轴上表示解集，熟练掌握知识点是解题的关键． 6. 一元二次方程 22 x A. 无实数根 5 x   的根的情况为（ 6 0 ） B. 有两个不等的实数根 C. 有两个相等的实数根 D. 不能判定【答案】A

【解析】【分析】先计算判别式的值，然后根据判别式的意义判断方程根的情况．【详解】解：∵Δ＝（−5）2−4×2×6＝-23＜0， ∴方程无实数根．故选：A．【点睛】本题考查了一元二次方程 ax2＋bx＋c＝0（a≠0）的根的判别式Δ＝b2−4ac：当Δ ＞0，方程有两个不相等的实数根；当Δ＝0，方程有两个相等的实数根；当Δ＜0，方程没有实数根． 7. 如图，在 O 中，弦 ,AB CD 相交于点 P，若（）   A 48 ,   APD  80  ，则 BÐ 的大小为 A. 32 【答案】A B. 42 C. 52 D. 62      A APD ，求得 C  32  ，再根据同弧【解析】【分析】根据三角形的外角的性质可得 C 所对的圆周角相等，即可得到答案． A 【详解】 C C   B      32  C      APD   32  A ， 48 ,   APD  80  ，故选：A．【点睛】本题考查了圆周角定理及三角形的外角的性质，熟练掌握知识点是解题的关键． 8. 下列命题，其中是真命题的是（） A. 对角线互相垂直的四边形是平行四边形 B. 有一个角是直角的四边形是矩形 C. 对角线互相平分的四边形是菱形 D. 对角线互相垂直的矩形是正方形【答案】D 【解析】【分析】分别根据平行四边形，矩形，菱形及正方形的判定定理进行判断即可．【详解】对角线互相平分的四边形是平行四边形，故 A 错误，不符合题意；有三个角是直角的四边形是矩形，故 B 错误，不符合题意；

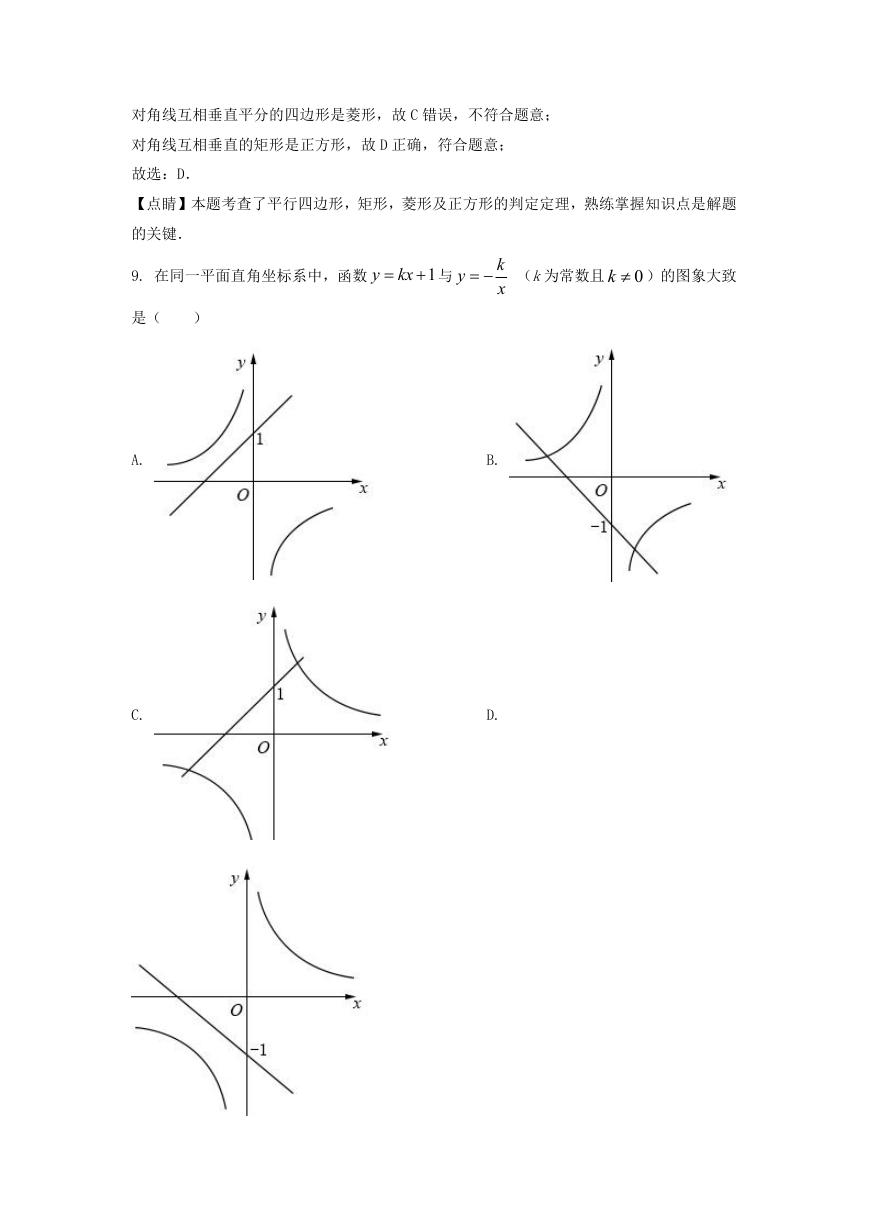
对角线互相垂直平分的四边形是菱形，故 C 错误，不符合题意；对角线互相垂直的矩形是正方形，故 D 正确，符合题意；故选：D．【点睛】本题考查了平行四边形，矩形，菱形及正方形的判定定理，熟练掌握知识点是解题的关键． 9. 在同一平面直角坐标系中，函数 y kx 1  与 y 是（）   （k为常数且 0 k  ）的图象大致 k x A. C. B. D.

【答案】A 【解析】【分析】根据题意中的函数解析式和函数图象的特点，可以判断哪个选项中的图象是正确的．【详解】解：根据函数 y kx 1  可得，该函数图象与 y轴的交点在 x轴上方，排除 B、D 选项，当 k＞0 时，函数 y kx 1  的图象在第一、二、三象限，函数 y   在第二、四象限，故 k x 选项 A 正确，故选：A．【点睛】本题考查反比例函数的图象、一次函数的图象，解答本题的关键是明确题意，利用数形结合的思想解答． 10. 今年我国小麦大丰收，农业专家在某种植片区随机抽取了 10 株小麦，测得其麦穗长（单位：cm）分别为 8，8，6，7，9，9，7，8，10，8，那么这一组数据的方差为（） B. 1.4 C. 1.3 D. 1.2 A. 1.5 【答案】D 【解析】【分析】根据方差的计算方法求解即可．【详解】解：这组数据的平均数为： 8 8 6 7 9 9 7 8 10 8           ， 8  8 8  2    4  6 8  2     2  2  7 8  10 方差 2 S  故选：D． 10  2  9 8    2  10 8  2   ， 1.2 【点睛】本题考查了方差的计算方法，熟练掌握求方差的公式是解题的关键． 11. 如图，抛物线 y  2 ax  bx  与 x轴相交于点  A c 小红同学得出了以下结论：① 2 b a b c 4    ．其中正确的个数为（ 0  ac  ；② 4 0 ）  B  2,0 ,   a b  ；③当 0 6,0 0 ，与 y轴相交于点 C， y  时， 2    ；④ 6x B. 3 C. 2 D. 1 A. 4 【答案】B 【解析】

【分析】根据二次函数的图像与性质，逐一判断即可．  与 x轴交于点 A c 【详解】解：∵抛物线 ax bx   y 2 2,0 、B 6,0 ， ∴抛物线对应的一元二次方程 2 ax  bx   有两个不相等的实数根， c 0 即 2 4 △  b ＞0 ，故①正确；对称轴为 x   ac b 2 a  6 2  2 ，整理得 4a＋b＝0，故②正确；由图像可知，当 y＞0 时，即图像在 x轴上方时， x＜－2 或 x＞6，故③错误， y 由图像可知，当 x＝1 时， ∴正确的有①②④，故选：B．    ＜，故④正确． a b c 0 【点睛】本题考查二次函数的性质与一元二次方程的关系，熟练掌握相关知识是解题的关键． 12. 正方形 ABCD 的对角线相交于点 O（如图 1），如果 BOC 绕点 O按顺时针方向旋转，其两边分别与边 ,AB BC 相交于点 E、F（如图 2），连接 EF，那么在点 E由 B到 A的过程中，线段 EF的中点 G经过的路线是（） A. 线段【答案】A B. 圆弧 C. 折线 D. 波浪线【解析】【分析】连接 ,OG BG ，根据题意可知线是OB 的线段垂直平分线的一段，即线段【详解】连接 ,OG BG ，根据题意可知   EBF   EOF  90  ， EBF   EOF  90  则线段 EF的中点 G经过的路

 OG BG   1 2 EF ， ∴点 G在线段 OB的垂直平分线上．则线段 EF的中点 G经过的路线是OB 的线段垂直平分线的一段，即线段．故选：A．【点睛】本题考查了线段垂直平分线的判定，直角三角形斜边上的中线等于斜边的一半，正方形的性质，掌握以上知识是解题的关键．二、填空题：本大题共 6 个小题，每小题 4 分，满分 24 分 13. 若二次根式 5x  在实数范围内有意义，则 x的取值范围为_____．【答案】x≥5 【解析】【分析】根据二次根式有意义的条件得出 x−5≥0，计算求解即可．【详解】解：由题意知， 5 0 解得， 5x  ，故答案为： 5x  ． x   ，【点睛】本题考查了二次根式有意义的条件，解一元一次不等式．熟练掌握二次根式有意义的条件是解题的关键． 14. 如图，屋顶钢架外框是等腰三角形，其中 AB AC BAC  ，则 C 的大小为_______． 120  ，立柱 AD BC ，且顶角【答案】30°##30 度【解析】【分析】先由等边对等角得到 B 【详解】 AB AC    ，， C B    ，再根据三角形的内角和进行求解即可． C

资料库

2022年山东滨州中考数学试题及答案.doc

相关推荐

中考

热门标签

最新资料