logo资料库

卡尔曼滤波..docx

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：0.10M 资料格式：docx 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    测试信号处理作业
    卡尔曼滤波器
    1 卡尔曼滤波器的介绍
    1.1 滤波的基础知识
    1.2 卡尔曼滤波器
    1.3 Kalman滤波起源及发展
    1.4 Kalman原理
    测试信号处理作业 作业题目：卡尔曼滤波的分析 组员： 组员： 组员： 指导老师： 专业： 测试计量技术及仪器
    卡尔曼滤波器 1 卡尔曼滤波器的介绍 1.1 滤波的基础知识 什么是滤波？滤波一词起源于通信理论，它是从含有干扰的接收信号中提取 有用的信号的一种技术。而更广泛地，滤波是指利用一定的手段抑制无用信号， 增强有用信号的数字信号处理过程。 无用信号，也叫噪声，是指观测数据对系统没有贡献或者起干扰作用的信号。 在通信中，无用信号也表现为特定波段频率、杂波：在传感器数据测量中，无用 信号表现为幅度干扰。例如，在温度测量中，传感器测量值与真实值之间往往有 一定的随机波动，这个波动就是随机干扰。其实噪声是一个随机的过程，而随机 过程有气功率谱密度函数，功率谱函数的形状决定了噪声的颜色。如果这些干扰 信号幅度分布服从高斯分布，而它的功率谱密度又是均匀分布的，则称它为高斯 白噪声。高斯白噪声是大多数传感器具有的一种测量噪声。 在工程应用中，如雷达测距、声呐测距、图像采集、声音录制等，只要是传 感器采集和测量的数据，都携带噪声干扰。这种影响有的很微小，有的则会使信 号变形、失真，有的严重导致数据不可用。那么滤波不是万能的，滤波只能最大 限度的降低噪声的干扰，即有的滤波是不能完全消除噪声，有的则可能完全消除。 1.2 卡尔曼滤波器 卡尔曼滤波器是一个“optimal recursive data processing algorithm(最优化自回 归数据处理算法)”。它能够从一系列的不完全及包含噪声的测量中，估计动态 系统状态。对于解决大部分问题，它是最优、效率最高甚至是最有用的。它的的 广泛应用已经超过 30 年，包括机器人导航、控制，传感器数据融合甚至在局势 方面的雷法系统及导航追踪等等。近年来更被应用于计算机图像处理，例如头脸 识别，图像分割，图像边缘检测等等。 本质上来讲，滤波就是一个信号处理与变换（去除或减弱不想要的成分，增 强所需成分）的过程，这个过程既可以通过硬件来实现，也可以通过软件来实现。
    卡尔曼滤波属于一种软件滤波方法，基本思想是：以最小均方差为最佳估计准则， 采用信号与噪声的状态空间模型，利用前一时刻的估计值和当前时刻的观测值来 更新对状态变量的估计，求出当前时刻的估计值，算法根据建立的系统方程和观 测方程对需要处理的信号做出满足最小均方差的估计。 1.3 Kalman 滤波起源及发展 1960 年，匈牙利数学家卡尔曼发表了一篇关于离散数据线性滤波递推算法 的论文，这意味着卡尔曼滤波的诞生。斯坦利.施密特(Stanley Schmidt)首次实现 了卡尔曼滤波器，卡尔曼在 NASA 埃姆斯研究中心访问时，发现他的方法对于 解决阿波罗计划的轨道预测很有用，后来阿波罗飞船的导航电脑使用了这种滤波 器。关于这种滤波器的论文由 Swerling (1958)、Kalman (1960)与 Kalman and Bucy (1961)发表. 卡尔曼滤波是一种有着相当广泛应用的滤波方法，但它既需要假定系统是线 性的，又需要认为系统中的各个噪声与状态变量均呈高斯分布，而这两条并不总 是确切的假设限制了卡尔曼滤波器在现实生活中的应用。扩展卡尔曼滤波器 （EKF）极大地拓宽了卡尔曼滤波的适用范围。EKF 的基本思路是，假定卡尔曼 滤滤对当前系统状态估计值非常接近于其真实值，于是将非线性函数在当前状态 估计值处进行台劳展开并实现线性化。另一种非线性卡尔曼滤波叫线性化卡尔曼 滤波。它与 EKF 的主要区别是前者将非线函数在滤波器对当前系统状态的最优 估计值处线性化，而后者因为预先知道非线性系统的实际运行状态大致按照所要 求、希望的轨迹变化，所以这些非线性化函数在实际状态处的值可以表达为在希 望的轨迹处的台劳展开式，从而完成线性化。 不敏卡尔曼滤波器（UKF）是针对非线性系统的一种改进型卡尔曼滤波器。 UKF 处理非线性系统的基本思路在于不敏变换，而不敏变换从根本上讲是一种 描述高斯随机变量在非线性化变换后的概率分布情况的方法。不敏卡尔曼滤波认 为，与其将一个非线性化变换线性化、近似化，还不如将高斯随机变量经非线性 变换后的概率分布情况用高斯分布来近似那样简单，因而不敏卡尔曼滤波算法没 有非线性化这一步骤。在每一定位历元，不敏卡尔曼滤波器按照一套公式产生一 系列样点，每一样点均配有一个相应的权重，而这些带权的样点被用来完整地描 述系统状态向量估计值的分布情况，它们替代了原先卡尔曼滤波器中的状态向量 估计值及协方差。不敏卡尔曼滤器让这些样点一一经历非线性状态方程与测量方 程，然后再将这些经非线性变换后的样点按照它们的权重而综合出对当前时刻的 系统状态向量估计值。 多态自适应（MMA）卡尔曼滤波器是一种受到广泛关注的滤波器，它由好
    多个并联、同时运行的卡尔曼滤波器组成。在这组卡尔曼滤波器中，每一个滤波 器对未知的滤波参数分别做出相互不同的假设，然后各自按照自己的模型假设进 行滤波计算，而多态自适应滤波器最后将它们对系统状态的各个估计值进行加权， 并以此作为最优估计值输出。 1.4 Kalman 原理 卡尔曼滤波是基于状态空间方法的一套递推滤波算法，在状态空间方法中， 引入了状态变量的概念。实际应用中，可以通过选取合适的状态变量来体现系统 的特征、特点和状况的变化。卡尔曼滤波的模型包括状态空间模型和观测模型。 状态模型是反映状态变化规律的模型，通过状态方程来描写相邻时刻的状态转移 变化规律；观测模型反映了实际观测量与状态变量之间的关系。Kalman 滤波问 题就是联合观测信息及状态转移规律来得到系统状态的最优估计。 假设动态系统的状态空间模型为 ( tX  )1  )( tX  )( tW )( tY  )( tHX  )( tV （1-1） （1-2） 其中， X(t) 系统在时刻 t 的状态 Y(t) 对状态的观测值 W(t) 系统噪声，方差阵为 Q V(t) 观测噪声，方差阵为 R  H 观测矩阵  系统噪声驱动矩阵 状态转移矩阵 卡尔曼滤波的计算流程为： 计算状态估计值： (ˆ tX  |1 t )1  (ˆ tX  )|1 t  ( tK  ()1 t   )1 （1-3） 计算状态一步预测： 计算新息： (ˆ tX  )|1 t  )|(ˆ t tX （1-4）
    ( t  )1  ( tY )1  (ˆ tXH  )|1 t 计算卡尔曼滤波增益： ( tK  )1  ( tP  )|1 Ht T [ ( tHP  )|1 Ht T  R 1]  计算一步预测均方误差： ( tP  )|1 t  )|( tP t T Q  T 计算一步预测估计均方误差： ( tP  |1 t  )1  [ I n  ( tK  )1 (] tPH  )|1 t 5 个经典的递推方程：          ˆ x ˆ x k H P P   k     ' k k k k k k 1 k  H y ( T ( k ˆ A x ˆ x '   k P C C P C ' ' k k A P A Q  k   I H C P '  k k T k 1  k k ˆ C x k T  k ' k R )  1 ) k k k  1 （1-5） （1-6） （1-7） （1-8） (1 ) a (1 ) b (1 ) c (1 ) d (1 ) e 为了更形象地说明卡尔曼滤波的原理，下面给出卡尔曼滤波的系统模型框图： 测 量 噪 声 输 入 量  过 程 噪 声 状 态 变 量 观 测 量  延时 H 系 统 二、方案设计 图 1 卡尔曼滤波的系统模型 卡尔曼滤波器（Kalman Filter）是一个最优化自回归数据处理算法（optimal recursive data processing algorithm）,它的广泛应用已经超过 30 年，包括航空器轨 道修正、机器人系统控制、雷达系统与导航追踪等。近年来更被应用与组合导航 与动态定位，传感器数据融合、微观经济学等应用研究领域。特别是在图像处理
    领域如头脸识别、图像分割、图像边缘检测等当前热门研究领域占有重要地位。 但是我们仅仅出入门的基础来理解卡尔曼，即对一个房间的温度测量进行滤 波。 假设我们研究的对象时一个房间的温度。根据经验判断，这个房间的温度大 概在 25°左右，可能受空气流通、阳光等因素影响，房间内温度会小幅度地波 动，我们以分钟为单位，定时测量房间的温度，这里的 1 分钟，可以理解为采样 时间。假设测量温度时，外界的天气是多云，阳光照射时有时无，同时房间不是 100%密封的，可能有微小的与外界空气的交换，即引入过程噪声 W(t) ，其方差 为 Q，大小假定位 Q=0.01（假如不考虑过程噪声的影响，即真实温度时恒定的， 那么这个时候 Q=0）。对照公式 1-1 和 1-2，相应地，A=1，T=1，Q=0.01，状态 X(t) 是 在 第 t 时 房 间 的 温 度 ， 是 一 维 的 。 那 么 该 系 统 的 状 态 方 程 可 以 写 为 X(t) X(t 1) W(t) 。现在用温度计开始测量房间的温度，假设温度计的测量误差   为±0.5℃，从出厂的说明书上我们得知该温度计的方差为 0.25。也就是说，温度 计第 K 次测量的数据不是 100%准确的，它是有测量噪声 V(t)，并且其方差 R=0.25， 因此测量方程 Z(t) X(t) V(t)       到此，我们很容易想到，该系统的状态和观测方程为 X(t) AX(t 1) W(t 1)    Z(t) HX(t) V(t)  式中，X(t) 是一维变量的温度；A=1;  =1;H=1; W(t) 和 V(t) 的方差为 Q 和 R; 模型建好以后，就可以用 Kalman 滤波了。假如要估算第 t 时刻房间的实际 温度值，首先要根据地 t-1 时刻的温度值来预测 K 时刻的温度。 （1）假定第 t-1 时刻的温度值为 23.9°C，房间的真实温度为 24.0°C，该 测量的的偏差为 0.1°C，协方差 P(t-1)=0.12. （2）在第 k 时刻，房间的真实温度为 24.1 度，温度计在该时刻测量的值为 24.5 度，偏差为 0.4。我们用于估算第 t 时刻的温度有两个温度值，分别是 t-1 时 刻的 23.9 度和第 t 时刻的 24.5 度。如何融合着两组数据，得到逼近真实的估计 值呢？ 首 先 ， 利 用 t-1 时 刻 的 温 度 值 预 测 第 t 时 刻 的 温 度 ， 其 预 计 的 偏 差 为 P(t|t-1)=P(t-1)+Q=0.02,计算 Kalaman 增益 K=P(t|t-1)/(P(t|t-1)+R)=0.0741，那么这 个 时 候 利 用 k 时 刻 的 观 测 值 ， 得 到 温 度 的 估 计 值 为 X(t)=23.9+0.0741*(24.1-23.9)=23.915。可见，与 23.9 度和 24.5 度相比较，Kalaman 估 计 值 23.915 更 接 近 真 实 值 24.1 度 。 此 时 更 新 t 时 刻 额 偏 差 P(k)=(1-K*H)P(t|t-1)=0.0186。最后由 X(t)=23.915 和 P(t)=0.0186，可以继续对下 一个时刻观测数据 z(t+1)进行更新和处理。
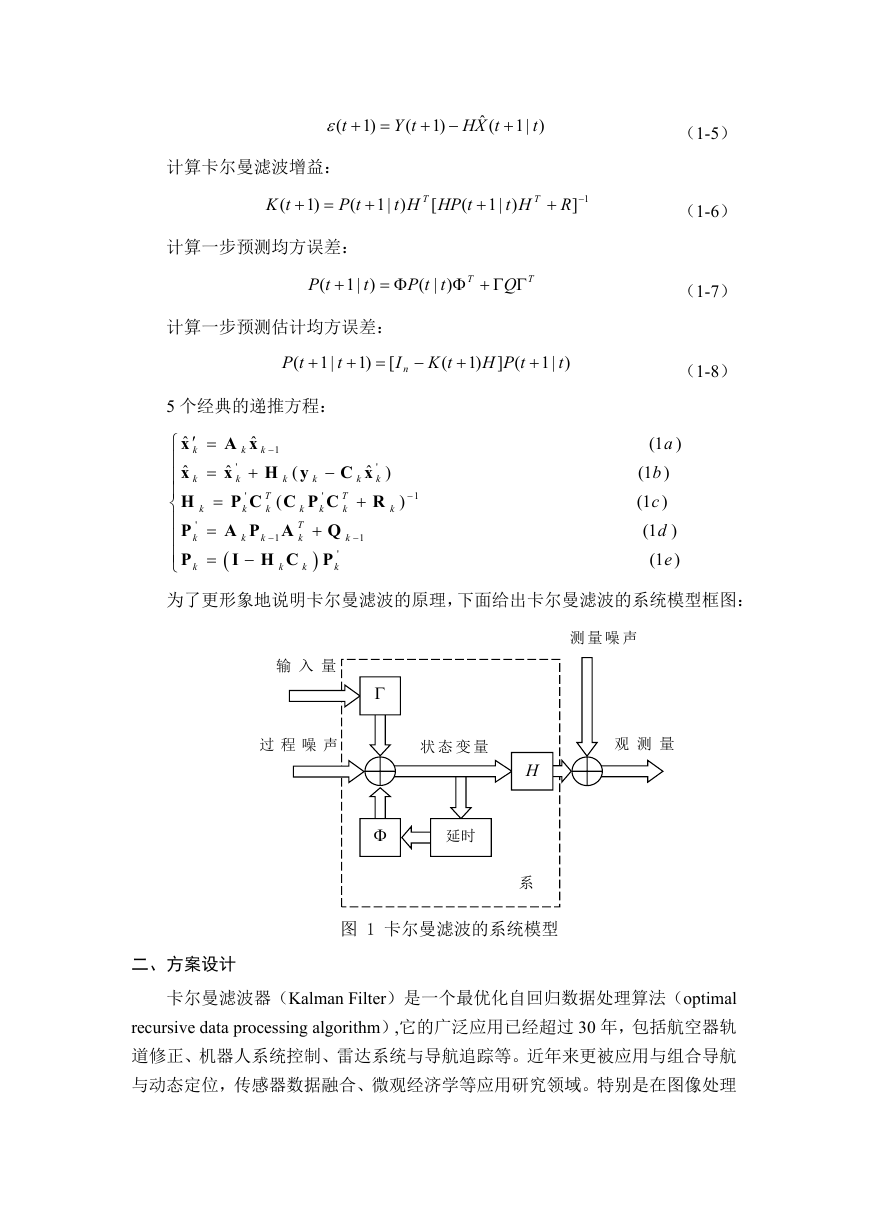
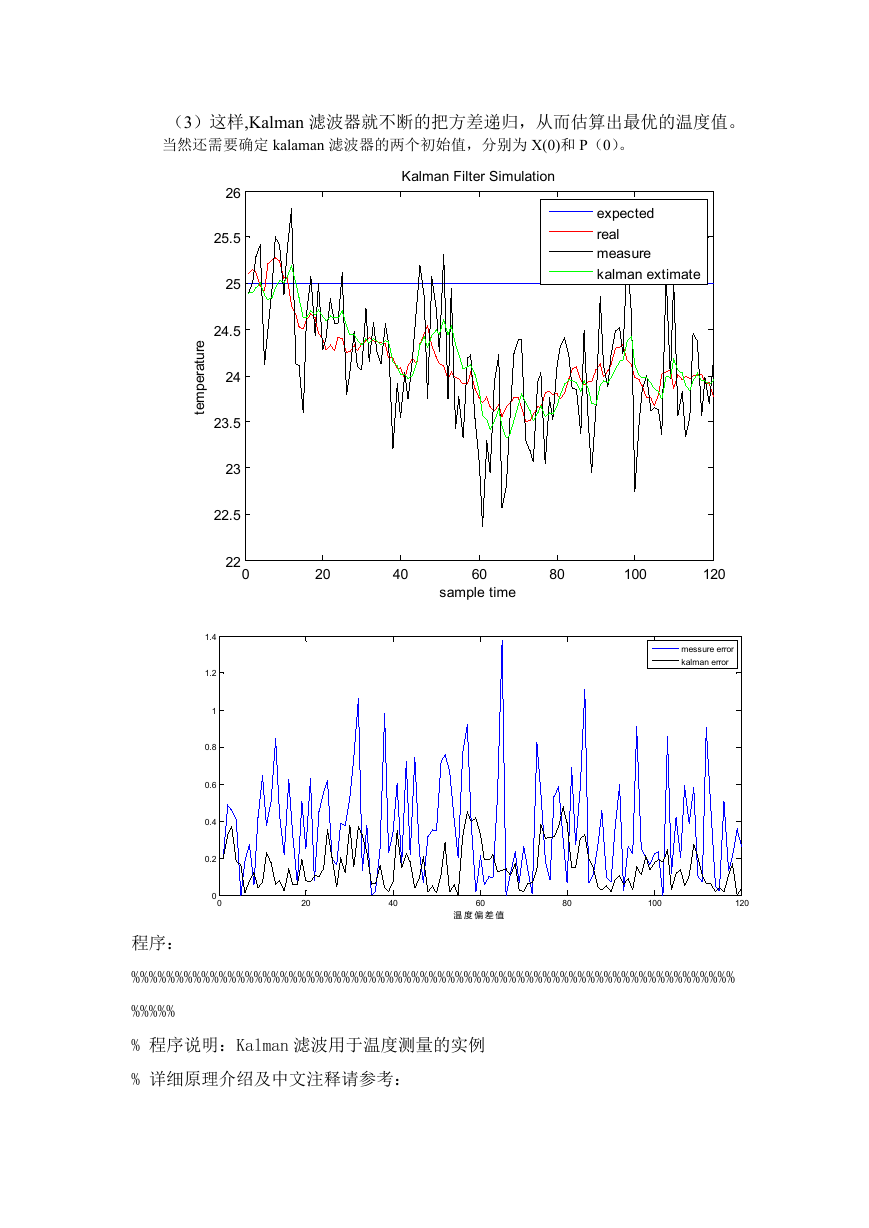
    （3）这样,Kalman 滤波器就不断的把方差递归，从而估算出最优的温度值。 当然还需要确定 kalaman 滤波器的两个初始值，分别为 X(0)和 P（0）。 e r u t a r e p m e t 26 25.5 25 24.5 24 23.5 23 22.5 22 0 1.4 1.2 1 0.8 0.6 0.4 0.2 0 0 Kalman Filter Simulation expected real measure kalman extimate 20 40 60 sample time 80 100 120 messure error kalman error 20 40 60 温 度 偏 差 值 80 100 120 程序： %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%% % 程序说明：Kalman 滤波用于温度测量的实例 % 详细原理介绍及中文注释请参考：
    % 《卡尔曼滤波原理及应用-MATLAB 仿真》，电子工业出版社，黄小平著。 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%% function main %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%% N=120;%采样点的个数，时间单位是分钟，可以理解为实验进行了 60 分钟的测量 CON=25;%室内温度测量的理论值，在这个理论值得基础上受过程噪声会有波动 %对状态和测量初始化 Xexpect=CON*ones(1,N);%期望的温度是恒定的 25°c,但真实温度不可能会这 样的 X=zeros(1,N); %房间各时刻真实温度值 Xkf=zeros(1,N);%Kalman 滤波处理的状态，也叫估计值 Z=zeros(1,N);%温度计测量值 P=zeros(1,N); %赋值值 X(1)=25.1;%假如初始值房间温度为 25.1°C P(1)=0.01;%初始值的协方差 Z(1)=24.9; Xkf(1)=Z(1);%初始值为 24.9°C，可以作为滤波器的初始状态 %噪声 Q=0.01; R=0.25; W=sqrt(Q)*randn(1,N);%方差决定噪声的大小 V=sqrt(R)*randn(1,N);%方差决定噪声大小 %系统矩阵 F=1; G=1; H=1; I=eye(1);%本系统状态为一维
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料