rd-cs算法.pdf-资料库

SAR 图像点目标仿真报告 1 SAR 原理简介合成孔径雷达(Synthetic Aperture Radar ，简称 SAR)是一种高分辨率成像雷达技术。它利用脉冲压缩技术获得高的距离向分辨率，利用合成孔径原理获得高的方位向分辨率，从而获得大面积高分辨率雷达图像。 SAR 回波信号经距离向脉冲压缩后，雷达的距离分辨率由雷达发射信号带宽决定： ρ = r C B 2 r ，式中 rρ 表示雷达的距离分辨率， rB 表示雷达发射信号带宽，C 表示光速。同样，SAR 回波信号经方位向合成孔径后，雷达的方位分辨率由雷达方位向的多谱勒带宽决定： ρ = ，式中 aρ 表示雷达的方位分辨率， aB 表示雷达方位向多谱勒带宽， av 表示 a v a B a 方位向 SAR 平台速度。在小斜视角的情况下，方位分辨率近似表示为 Dρ = ，其中 D 为 a 2 方位向合成孔径的长度。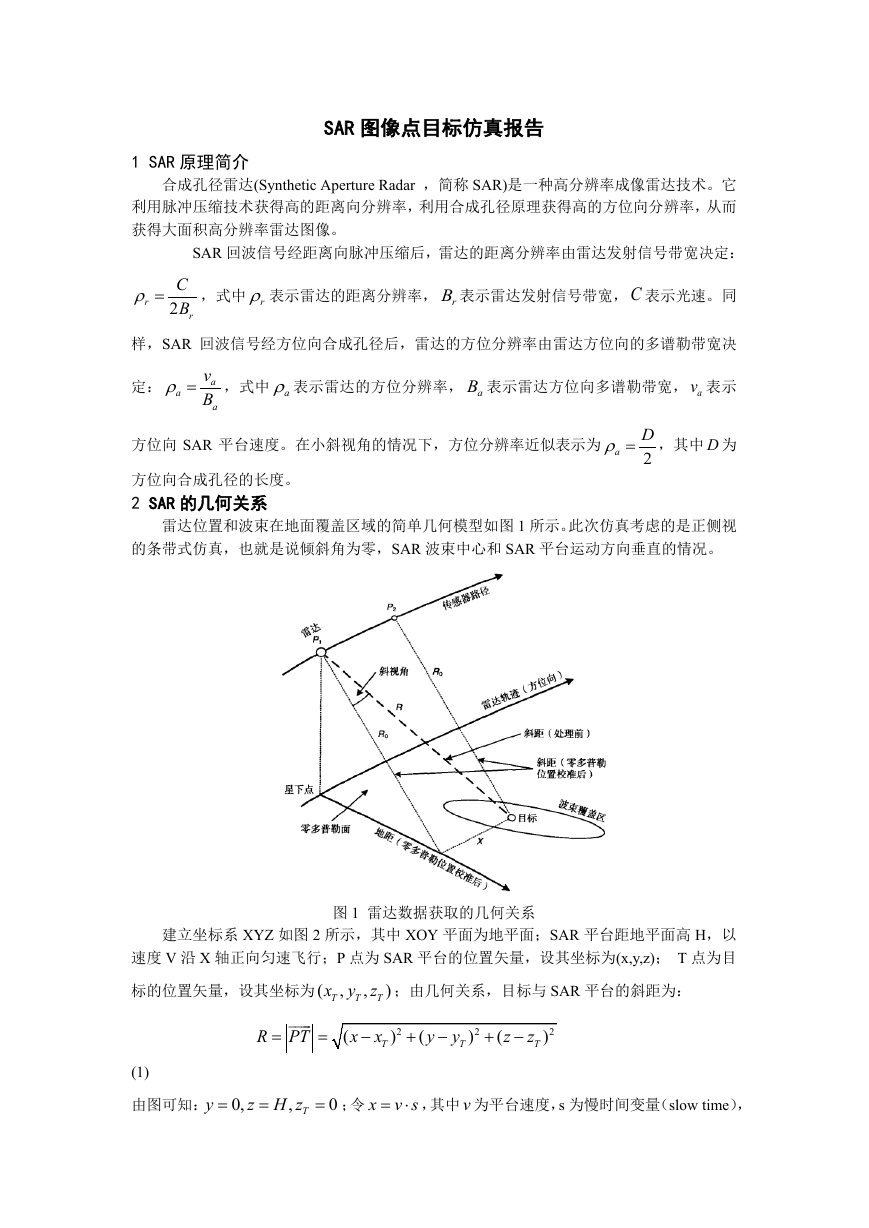 2 SAR 的几何关系雷达位置和波束在地面覆盖区域的简单几何模型如图 1 所示。此次仿真考虑的是正侧视的条带式仿真，也就是说倾斜角为零，SAR 波束中心和 SAR 平台运动方向垂直的情况。图 1 雷达数据获取的几何关系建立坐标系 XYZ 如图 2 所示，其中 XOY 平面为地平面；SAR 平台距地平面高 H，以速度 V 沿 X 轴正向匀速飞行；P 点为 SAR 平台的位置矢量，设其坐标为(x,y,z)； T 点为目标的位置矢量，设其坐标为 ( y z ；由几何关系，目标与 SAR 平台的斜距为： T x T , , ) T  R PT = = ( x − x T 2 ) + ( y − y T 2 ) + ( z − z T 2 ) z H z , = T = ；令 x 0 = ⋅ ，其中 v 为平台速度，s 为慢时间变量（slow time）， v s (1) 由图可知： 0, = y

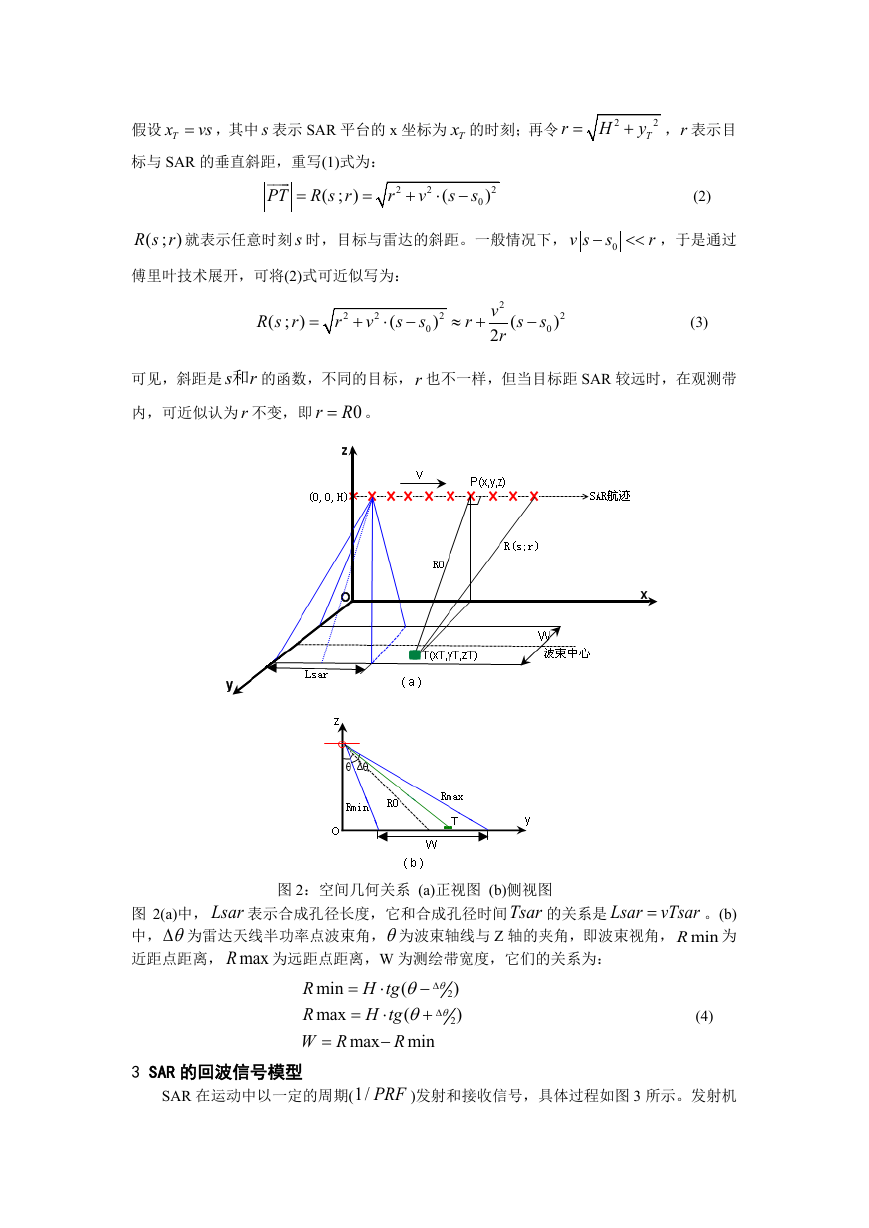
vs= ，其中 s 表示 SAR 平台的 x 坐标为 Tx 的时刻；再令 r = 2 H + 2 y T ，r 表示目假设 Tx 标与 SAR 的垂直斜距，重写(1)式为： r R s r ( ; )  PT = = 2 + 2 v ( ⋅ − s 2 s 0 ) (2) R s r 就表示任意时刻 s 时，目标与雷达的斜距。一般情况下， ( ; ) v s − s 0 << ，于是通过 r 傅里叶技术展开，可将(2)式可近似写为： R s r ( ; ) = 2 r + 2 v ( ⋅ − s 2 s 0 ) ≈ + r v 2 2 r ( s − 2 s 0 ) (3) r和的函数，不同的目标，r 也不一样，但当目标距 SAR 较远时，在观测带可见，斜距是 s 内，可近似认为 r 不变，即 r R= 。 0 图 2：空间几何关系 (a)正视图 (b)侧视图图 2(a)中， Lsar 表示合成孔径长度，它和合成孔径时间Tsar 的关系是 Lsar 中， θ∆ 为雷达天线半功率点波束角，θ为波束轴线与 Z 轴的夹角，即波束视角， minR 近距点距离， max 为远距点距离，W 为测绘带宽度，它们的关系为： vTsar R = 。(b) 为 R min R max W R = = = max H tg ( θ ⋅ − H tg ( θ ⋅ + R min − ∆ θ 2 ∆ θ 2 ) ) (4) 3 SAR 的回波信号模型 SAR 在运动中以一定的周期(1/ PRF )发射和接收信号，具体过程如图 3 所示。发射机

以 lτ 的时间发射啁啾脉冲，然后切换天线开关接收回波信号。图 3 雷达发射脉冲串的时序当雷达不处于发射状态时，它接收 3 反射回波。发射和接收回波的时间序列如图 4 所示。在机载情况下，每个回波可以在脉冲发射间隔内直接接收到。但是在星载情况下，由于距离过大，某个脉冲的回波要经过 6~10 个脉冲间隔才能接收到。这里仿真为了方便，默认为机载情况。图 4 脉冲雷达的发射与接收周期假设 rT 为 chirp 信号持续时间，下标 r 表示距离向；PRF 为重复频率，PRT 为重复周期，等于1/ PRF 。接收序列中， τ = n R s r 2* ( ; ) C 表示发射第i 个脉冲时，目标回波相对于发射序列的延时。雷达的发射序列数学表达式为式(5): s t ( ) = ∞ ∑ n =−∞ p t n PRT ( − * ) p (t) = rect( t T r j K π r 2 t )e j 2 π f t c e （5）式中， rect( ) 表示矩形信号， rK 为距离向的 chirp 信号调频率， cf 为载频。雷达回波信号由发射信号波形，天线方向图，斜距，目标 RCS，环境等因素共同决定，若不考虑环境因素，则单点目标雷达回波信号可写成式(6)所示： s t ( ) r = ∞ ∑ n =−∞ σ wp t n PRT − ⋅ ( τ − n ) (6) 其中，σ表示点目标的雷达散射截面， w 表示点目标天线方向图双向幅度加权， nτ 表示载机发射第 n 个脉冲时，电磁波再次回到载机时的延时 τ = n R s r 2* ( ; ) C ，带入式(6)中得：

∞ = s t ( ) r ∑ =−∞ exp[ n ⋅ σ w rect ⋅ ( t n PRT − ⋅ R s r C 2 ( ; ) / − T r R s r C 2 ( ; ) / − ) ⋅ 2 ) ] ⋅ (7) exp[- R s r j ( ; )] exp[ 2 ⋅ f π t n PRT ( − ⋅ c τ − n )] − ⋅ j K t n PRT ( π r 4 π λ j exp[ 4 R s rπ ( ; )] λ 式(7)就是单点目标回波信号模型，其中， j K t n PRT π − ⋅ ( − R s r C 2 ( ; ) / 2 ) ] 是 r chirp 分量，它决定距离向分辨率； exp[- j 为多普勒分量，它决定方位向分辨率。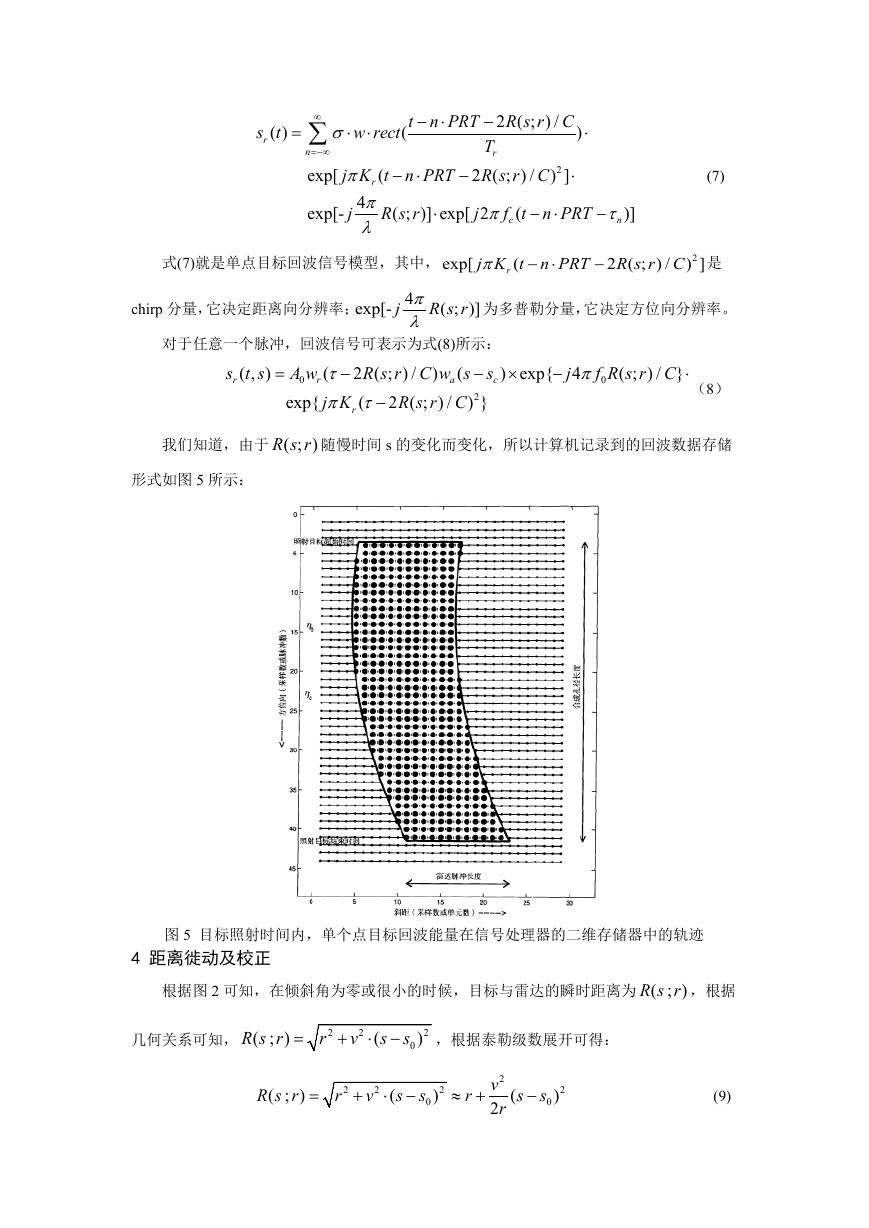对于任意一个脉冲，回波信号可表示为式(8)所示： s − c 2 ) } R s r C w s 2 ( ; ) / ( a R s r C 2 ( ; ) / ( s t s A w ( , ) r r 0 exp{ ( τ − j K π τ − = ) r ) exp{ × − j 4 π f R s r C ( ; ) / } 0 ⋅ （8）我们知道，由于 ( ; ) R s r 随慢时间 s 的变化而变化，所以计算机记录到的回波数据存储形式如图 5 所示：图 5 目标照射时间内，单个点目标回波能量在信号处理器的二维存储器中的轨迹 4 距离徙动及校正根据图 2 可知，在倾斜角为零或很小的时候，目标与雷达的瞬时距离为 ( ; ) R s r ，根据几何关系可知， R s r ( ; ) = 2 r + 2 v ( ⋅ − s 2 s 0 ) ，根据泰勒级数展开可得： R s r ( ; ) = 2 r + 2 v ( ⋅ − s 2 s 0 ) ≈ + r v 2 2 r ( s − 2 s 0 ) (9)

由式(9)可知，不同慢时间对应着不同的 ( ; ) R s r ，并且是一个双曲线形式或者近似为一个二次形式。如图 5 所示，同一目标的回波存储在计算机里不在同一直线上，存在距离徙动。从而定义距离徙动量： R s r ( , ) ∆ = v 2 2 r ( s − 2 s 0 ) （10）为了进行方位向的压缩，方位向的回波数据必须在同一条直线上，也就是说必须校正距 R s r 离徙动 ( , ) ∆ R s r 。由式（10）可知，不同的最近距离 r 对应着不同的 ( , ) ∆ ，因此在时域处理距离徙动会非常麻烦。因此，对方位向进行傅里叶变换，对距离向不进行变换，得到新的域。由于方位向的频率即为多普勒频率，所以这个新的域也称为距离多普勒域。将斜距 R 写成多普勒 fa 的函数，即 ( 回波多普勒 af 是倾斜角θ的函数，即 R f ( a r , ) = r / cos θ = r / 1 ( − = = r f a θ θ r , ) / cos aR f ，斜距 ( aR f r 。众所周知，对最近距离为 r 的点目标 P， , ) V 2 sin λ r / 1 sin = f λ ) a V 2 2 rf (11) ，于是 θ − 2 ≈ + r 1 8 ( 2 2 a λ ) V aR f ∆ 所以距离多普勒域中的我距离徙动为 ( r , ) = 1 ( 8 λ ) V 2 2 arf ，可发现它不随慢时间变换，同一最短距离 r 对应着相同大小的距离徙动。因此在距离多普勒域对一个距离徙动校正就是对一组具有相同最短距离的点目标的距离徙动校正，这样可以节省运算量。为了对距离徙动进行校正，需要得到距离徙动单元，即距离徙动体现在存储单元中的移 R f 动数值，距离徙动单元可以表示为 ( ∆ ，这个值通常为一个分数，由于存储单元 r ρ , ) / r a 都是离散的，所以不同通过在存储单元简单的移动得到准确的值。为了得到准确的徙动校正值，通常需要进行插值运算。本仿真采用了两种插值方法最近邻点插值和 sinc 插值，下面分别进行介绍。最近邻点 + ，其中 N 为整数部分， R f 插值法的优点是简单而快速，缺点是不够精确。 ( ∆ N n = r , ) / a ρ r n 为小数部分，整数部分徙动可以直接通过平移消除，对于小数部分则通过四舍五入的方法变为 0 或者 1，这样就可以得到较为精确的插值。 Sinc 插值原理如下：在基带信号下，卷积核是 sinc 函数 h x ( ) = c x sin ( ) = ) x sin( π x π 插值信号为 g x ( ) = ∑ i g i d ( )sin ( c x i − ) （12）（13）即为所有输入样本的加权平均。可通过频域来理解，如图 6 所示，采样信号 ( ) dg i 的频谱 ( dG f 等于以采样率重复的信 )

号频谱。为了重建信号 ( )g x ，只需要一个周期频谱（如基带周期），因此需要理想矩形低通滤波器在频域中提取基带频谱（如图 6）所示。已知该理想滤波器在时域中是 sinc 函数。由于频域相乘相当于时域卷积，故插值可以通过与 sinc 核的卷积来实现。图 6 理想低通滤波器怎样对采样信号进行插值 5 点目标成像 matlab 仿真 5.1 距离多普勒算法距离多普勒算法（RDA）是在 1976 年至 1978 年为民用星载 SAR 提出的，它兼顾了成熟、简单、高效和精确等因素，至今仍是使用最广泛的成像算法。它通过距离和方位上的频域操作，到达了高效的模块化处理要求，同时又具有了一维操作的简便性。图 7 示意了 RDA 的处理流程。这里主要讨论小倾斜角及短孔径下的基本 RDA 处理框图。进行距离向匹配滤波，再利用距离 IFFT 完成距离压缩。回波信号为： 1.当数据处在方位时域时，可通过快速卷积进行距离压缩。也就是说，距离 FFT 后随即 R s s t s A w t 2 ( ) / ] ( , ) [ − 0 0 c f R s j exp{- 4 π 0 s ) − c j K t ( ) / }exp{ π c w s ( = × a r r 2 ( - 2 ( ) / ) } R s c 距离向压缩后的信号为： t s s ( , ) rc = = IFFT S f s H f ( , ) )} t c w s R s A 2 ( ) / ] ( 0 { ( t 0 t [ − ρ r a t − s c )exp{ − j 4 π f R s 0 c ( ) / } （14）（15） H f ( t ) = rect { | f K T | }exp{ − j π 2 f K }exp{ − j ft 2 π } 0 （16） 2.通过方位 FFT 将数据变换至距离多普勒域，多普勒中心频率估计以及大部分后续操作都在该域进行。方位向傅里叶变换后信号为： t s ( , )} R f 2 ( rd c f R 4 π 0 0 c exp{- FFT s { rc A p t [ 0 S t ( , 1 = = × − ) f j s r s ) s W f ] ( a s − f s c ) （17） }exp{ j π f s K 2 a } 3.在距离多普勒域进行随距离时间及方位频率变化的 RCMC，该域中同一距离上的一组目标轨迹相互重合。RCMC 将距离徙动曲线拉直到与方位频率轴平行的方向。这里可以采用最近邻点插值法或者 sinc 插值法，具体插值方法见前面。假设 RCMC 插值是精确的，信号变为：

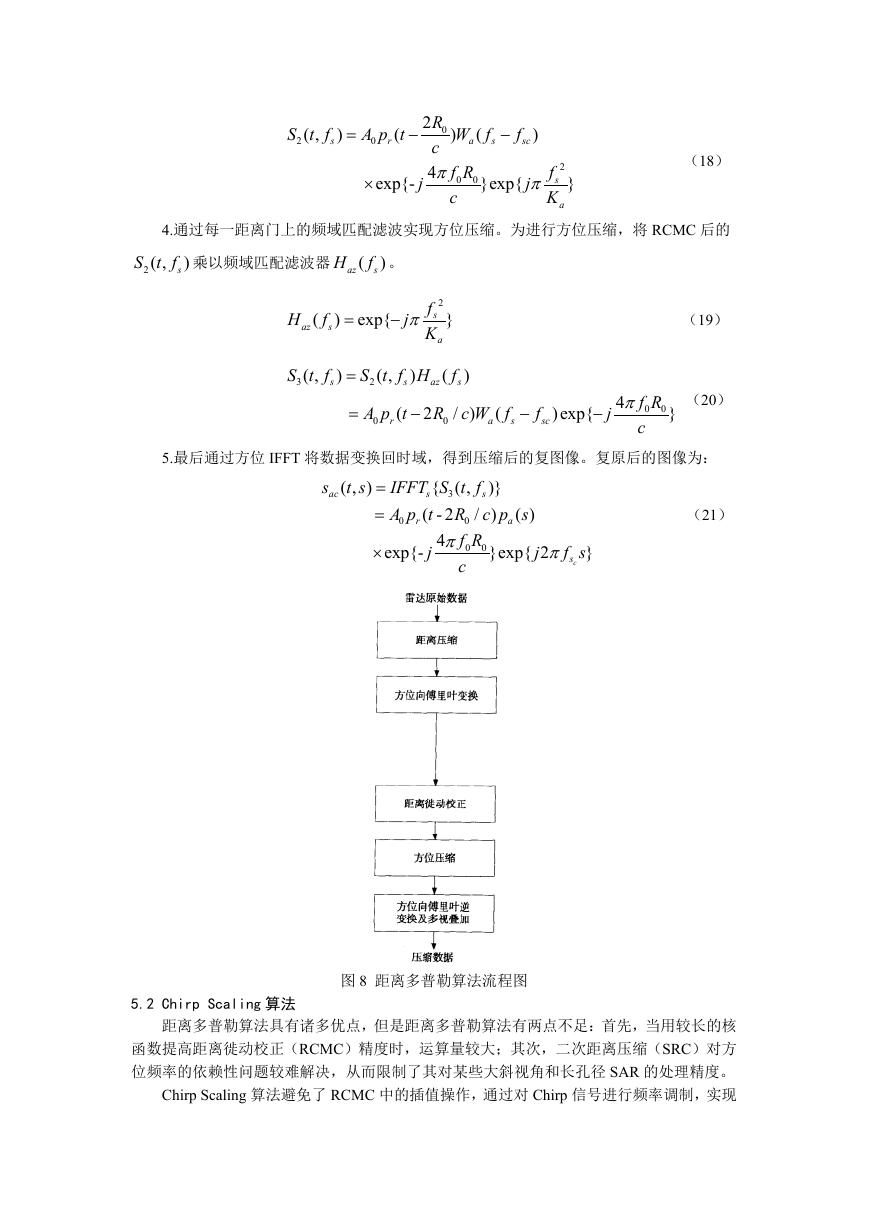
S t ( , 2 f s ) = A p t ( 0 r − W f ) ( − f sc ) s 2 a R 0 c f R 4 π 0 0 c exp{- × j （18） }exp{ j π f s K 2 a } S t 2( , 4.通过每一距离门上的频域匹配滤波实现方位压缩。为进行方位压缩，将 RCMC 后的 f 乘以频域匹配滤波器 ( )s az H f 。 ) s H f ( az s ) = exp{ − j π 2 f }s K a （19） S t ( , 3 f s ) = S t ( , 2 f H f ( s ) az ) s = A p t ( 0 r − 2 R c W f ( 0 / ) a − f sc )exp{ − j s （20） f R 4 π 0 0 c } 5.最后通过方位 IFFT 将数据变换回时域，得到压缩后的复图像。复原后的图像为： t s s ( , ) ac = = r f )} s / ) IFFT S t { ( , s 3 R c p s A p t ( - 2 ( ) 0 0 f R 4 π 0 0 c j a exp{- × j }exp{ 2 π f s }c s （21）图 8 距离多普勒算法流程图 5.2 Chirp Scaling 算法距离多普勒算法具有诸多优点，但是距离多普勒算法有两点不足：首先，当用较长的核函数提高距离徙动校正（RCMC）精度时，运算量较大；其次，二次距离压缩（SRC）对方位频率的依赖性问题较难解决，从而限制了其对某些大斜视角和长孔径 SAR 的处理精度。 Chirp Scaling 算法避免了 RCMC 中的插值操作，通过对 Chirp 信号进行频率调制，实现

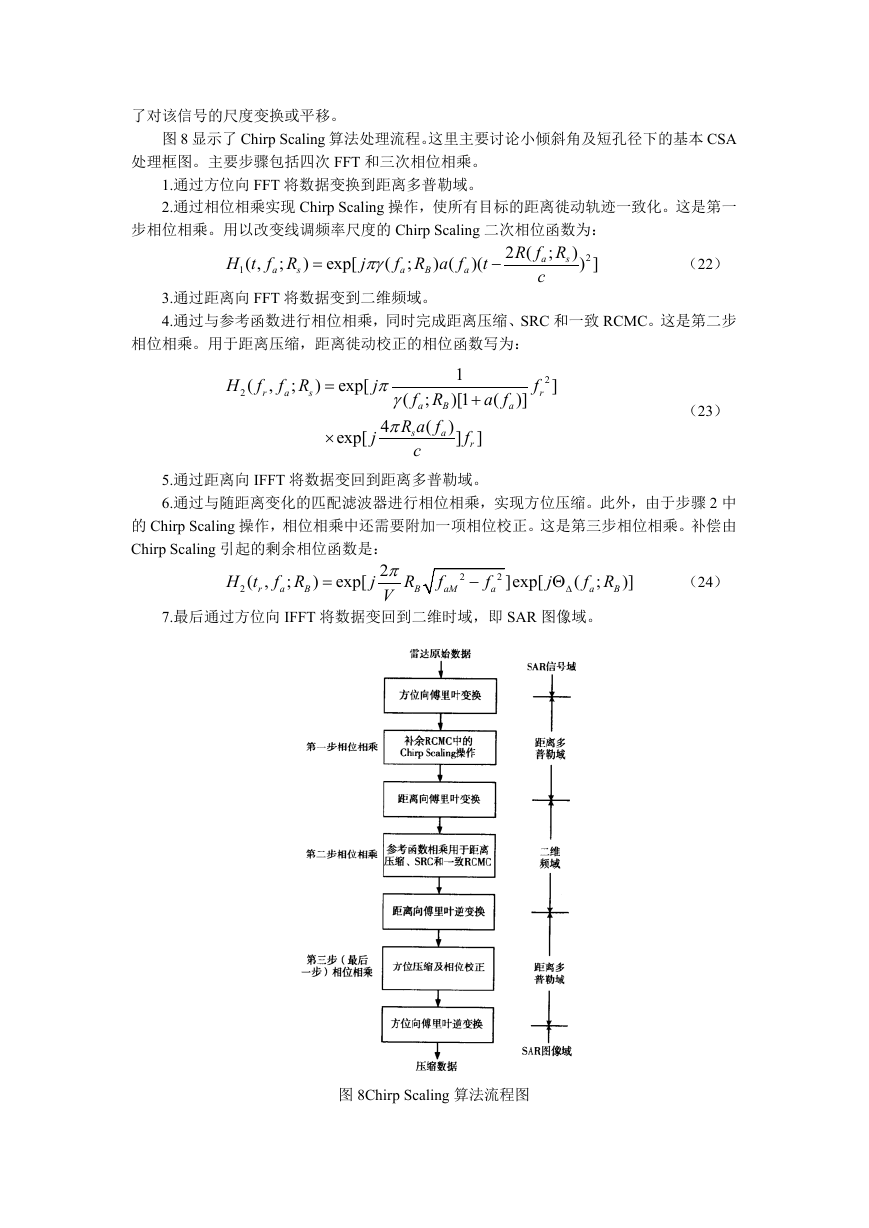
了对该信号的尺度变换或平移。图 8 显示了 Chirp Scaling 算法处理流程。这里主要讨论小倾斜角及短孔径下的基本 CSA 处理框图。主要步骤包括四次 FFT 和三次相位相乘。 1.通过方位向 FFT 将数据变换到距离多普勒域。 2.通过相位相乘实现 Chirp Scaling 操作，使所有目标的距离徙动轨迹一致化。这是第一步相位相乘。用以改变线调频率尺度的 Chirp Scaling 二次相位函数为： H t ( , 1 f R a s ; ) = exp[ j ( πγ f R a f ) ( a ; B t )( − a R f R 2 ( s ; a c ) 2 ) ] （22） 3.通过距离向 FFT 将数据变到二维频域。 4.通过与参考函数进行相位相乘，同时完成距离压缩、SRC 和一致 RCMC。这是第二步相位相乘。用于距离压缩，距离徙动校正的相位函数写为： H f ( 2 r , f R a s ; ) = exp[ exp[ × j j π 1 f R ( ; )[1 γ a B R a f 4 ( ) π s c ] f a f r 2 ] + a f ( )] a ] r （23） 5.通过距离向 IFFT 将数据变回到距离多普勒域。 6.通过与随距离变化的匹配滤波器进行相位相乘，实现方位压缩。此外，由于步骤 2 中的 Chirp Scaling 操作，相位相乘中还需要附加一项相位校正。这是第三步相位相乘。补偿由 Chirp Scaling 引起的剩余相位函数是： 2 π V （24） H t ( , r f R a B f R a B ]exp[ exp[ R B j Θ )] = 2 f a ( ∆ 2 − f aM j ; 2 ; ) 7.最后通过方位向 IFFT 将数据变回到二维时域，即 SAR 图像域。图 8Chirp Scaling 算法流程图

资料库

rd-cs算法.pdf

相关推荐

课程资源

热门标签

最新资料