python数据分析实战之AQI预测.pdf-资料库

weixin_38681082-13743495-16359647290472275083.pdf-第1页.png

第1页 / 共6页

weixin_38681082-13743495-16359647290472275083.pdf-第2页.png

第2页 / 共6页

weixin_38681082-13743495-16359647290472275083.pdf-第3页.png

第3页 / 共6页

weixin_38681082-13743495-16359647290472275083.pdf-第4页.png

第4页 / 共6页

weixin_38681082-13743495-16359647290472275083.pdf-第5页.png

第5页 / 共6页

weixin_38681082-13743495-16359647290472275083.pdf-第6页.png

第6页 / 共6页

python数据分析实战之数据分析实战之AQI预测预测前言：上一篇对AQI进行了分析，这一篇根据对以往的数据，建立一个模型，可以将模型应用于未知的数据，来进行AQI的预测。文章目录1、加载相关库和数据集2、数据处理和转换2.1 简单的数据处理2.2 数据转换3、建立基模型4、特征选择4.1 RFECV4.2 文章目录使用RFECV进行特征选择5、异常值处理5.1 使用临界值进行填充5.2 分箱离散化6 、残差图分析6.1 异方差性6.2 离群点 1、加载相关库和数据集、加载相关库和数据集使用的库主要有：pandas、numpy、matplotlib、seaborn、sklearn 使用的数据集：2015年空气质量指数（AQI）数据集 import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import warnings sns.set(style="darkgrid") plt.rcParams["font.family"] = "SimHei" # 设置可以显示中文字体 plt.rcParams["axes.unicode_minus"] = False warnings.filterwarnings("ignore") # 忽略警告信息 data = pd.read_csv("AQI_data.csv") # AQI历史数据集 2、数据处理和转换、数据处理和转换 2.1 简单的数据处理简单的数据处理 # 空值、重复值处理 data.fillna({"Precipitation": data["Precipitation"].median()}, inplace=True) data.drop_duplicates(inplace=True) 2.2 数据转换数据转换对于模型来说，内部进行的都是数学上的运算，所以在进行建模之前，我们需要对类别变量进行数据转换，变成离散变量。 # 将类别变量（是，否）转成离散变量（1，0） data["Coastal"] = data["Coastal"].map({"是": 1, "否": 0}) data["Coastal"].value_counts() 3、建立基模型、建立基模型不进行任何处理，建立一个基模型，后续的操作都可以在此基础上进行改进。 from sklearn.linear_model import LinearRegression from sklearn.model_selection import train_test_split X = data.drop(["City","AQI"], axis=1) # 城市名称对结果不会有影响，所以去除城市列 y = data["AQI"] # 切分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0) lr = LinearRegression() lr.fit(X_train, y_train) # 使用训练集训练模型 print("训练集R^2：",lr.score(X_train, y_train)) print("测试集R^2：",lr.score(X_test, y_test)) ------------------------ 训练集R^2： 0.4685357478390665 测试集R^2： 0.3075998035417721 y_hat = lr.predict(X_test) plt.figure(figsize=(15, 5)) plt.plot(y_test.values, "-r", label="真实值", marker="o") plt.plot(y_hat, "-g", label="预测值", marker="D") plt.legend(loc="upper left") plt.title("线性回归预测结果", fontsize=20)

4、特征选择、特征选择建立基模型时选择了所有的特征建立模型，但是特征并非越多越好，有些特征可能对模型质量并没有什么改善，我们可以进行删除，同时也可以提高模型训练速度。特征选择的方式有很多，常用的有RFECV方法 4.1 RFECV RFECV分成两个部分，分别为RFE和CV。 RFE（Recursive Feature Elimination）：递归特征消除，用来对特征进行重要性评级。（1）初始的特征集为所有可用的特征（2）使用当前特征集进行建模，然后计算每个特征的重要性。（3）删除最不重要的一个（或多个）特征，更新特征集。（4）跳转到步骤（2），直到完成所有特征的重要性评级。 CV（Cross Validation）：交叉验证，在特征评级后，通过交叉验证，选择最佳数量的特征。（1）根据RFE阶段确定的特征重要性，依次选择不同数量的特征。（2）对选定的特征集进行交叉验证（3）确定平均分最高的特征数量，完成特征选择。 4.2 使用使用RFECV进行特征选择进行特征选择 from sklearn.feature_selection import RFECV # estimator：要操作的模型，step：每次删除的变量数，cv：使用的交叉验证折数 # n_jobs：并发的数量， scoring: 评估的方式。 rfecv = RFECV(estimator=lr, step=1, cv=5, n_jobs=-1, scoring="r2") rfecv.fit(X_train, y_train) print(rfecv.n_features_) # 经过选择之后，剩余的特征数量。 ------------------- 9 print(rfecv.estimator_) # 经过特征选择后，使用缩减特征训练后的模型。 ---------------------- LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False) print(rfecv.ranking_) # 每个特征的等级，数值越小，特征越重要。 ----------------------- [1 1 1 1 1 1 2 1 1 1] print(rfecv.support_) # 布尔数组，用来表示特征是否被选择。 ------------------------ [ True True True True True True False True True True] print(rfecv.grid_scores_) # 对应数量特征时，模型交叉验证的评分。 ----------------------------------- [0.05508632 0.21749262 0.2838958 0.28166965 0.28155987 0.26612634 0.26932041 0.31413689 0.31538241 0.30976458] 5、异常值处理、异常值处理

如果数据中存在异常值，有可能会对模型效果产生影响，所以建模时非常有必要对异常值进行处理。根据前面分析的介绍，可以使用临界值进行填充和使用分箱法离散化对异常值处理 5.1 使用临界值进行填充使用临界值进行填充依据箱线图判断离群点的原则去发现异常值，然后使用临界值对异常值进行填充替换。需要注意的是，应该使用训练集数据去计算临界值，我们在训练期间永远不能使用测试集。箱线图可以用来观察数据整体的分布情况，利用中位数，25/%分位数（Q1），75/%分位数（Q3），上边界，下边界等统计量来描述数据的整体分布情况。箱线图合理范围为 [Q1 – 1.5 IQR, Q3 + 1.5 IQR] （IQR = Q3 − Q1） # Coastal是类别变量，映射为离散变量，不会有异常值。 for col in X.columns.drop("Coastal"): if pd.api.types.is_numeric_dtype(X_train[col]): quartile = np.quantile(X_train[col], [0.25, 0.75]) IQR = quartile[1] - quartile[0] # 计算 IQR lower = quartile[0] - 1.5 * IQR # 计算下边界 upper = quartile[1] + 1.5 * IQR # 计算上边界 X_train[col][X_train[col] upper] = upper # 对大于上边界的数用上边界值进行替换 X_test[col][X_test[col] upper] = upper 使用临界值处理之后的训练集再次进行训练，观察是否有改进： lr.fit(X_train, y_train) # 再次使用训练集训练模型 print("训练集R^2：",lr.score(X_train, y_train)) print("测试集R^2：",lr.score(X_test, y_test)) ------------------------------------------- # 相比处理之前有轻微改善，但不是很明显训练集R^2： 0.48091353214900345 测试集R^2： 0.3284512692284217 再次使用RFECV进行特征选择： # estimator：要操作的模型，step：每次删除的变量数，cv：使用的交叉验证折数 # n_jobs：并发的数量， scoring: 评估的方式。 rfecv = RFECV(estimator=lr, step=1, cv=5, n_jobs=-1, scoring="r2") rfecv.fit(X_train, y_train) print(rfecv.n_features_) # 经过选择之后，剩余的特征数量。 ---------------------------- 9 print(rfecv.estimator_) # 经过特征选择后，使用缩减特征训练后的模型。 ---------------------------- LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False) print(rfecv.ranking_) # 每个特征的等级，数值越小，特征越重要。 -------------------------------------- [1 1 1 1 1 1 2 1 1 1] print(rfecv.support_) # 布尔数组，用来表示特征是否被选择。 --------------------------------------- [ True True True True True True False True True True] print(rfecv.grid_scores_) # 对应数量特征时，模型交叉验证的评分 ------------------------------------------------------- [0.05508632 0.2109287 0.25972937 0.23394533 0.2541774 0.25827203 0.35205041 0.3593648 0.3769399 0.36918705] print("剔除的变量：", X_train.columns[~rfecv.support_]) ----------------------------------- 剔除的变量： Index(['PopulationDensity'], dtype='object') 经过临界值处理和RFECV进行特征选择之后，效果改进仍然不是很明显，可以使用分箱离散化进行进一步处理。 5.2 分箱离散化分箱离散化分箱离散化是一种数据预处理技术，用于减少次要观察误差的影响，是一种将多个连续值分组为较少数量的“分箱”的方法（如将人的年龄按照一定的区间进行分组）。分箱后，不能将每个区间都映射为离散数值，而是应当使用One-Hot编码。将离散型特征使用one-hot编码，是为了让特征之间的距离计算更加合理，详情请戳机器学习：数据预处理之独热编码（One- Hot） from sklearn.preprocessing import KBinsDiscretizer

k = KBinsDiscretizer(n_bins=[4, 5, 14, 6], encode="onehot-dense", strategy="uniform") """ KBinsDiscretizer K个分箱的离散器，用于将数值变量（通常是连续变量）进行区间离散化操作。 n_bins：分箱（区间）的个数 encode：离散化编码方式,分为：onehot（使用独热编码，返回稀疏矩阵。）， onehot-dense（使用独热编码，返回稠密矩阵）， ordinal（使用序数编码（0,1,2……））。 strategy：分箱的方式，分为：uniform（每个区间的长度范围大致相同。）， quantile（每个区间包含的元素个数大致相同。）， kmeans（使用一维kmeans方式进行分箱）。 """ discretize = ["Longitude", "Temperature", "Precipitation", "Latitude"] # 定义离散化的特征 X_train_eli = X_train[X_train.columns[rfecv.support_]] # 特征选择剔除后的数据 X_test_eli = X_test[X_test.columns[rfecv.support_]] r = k.fit_transform(X_train_eli[discretize]) r = pd.DataFrame(r, index=X_train_eli.index) X_train_dis = X_train_eli.drop(discretize, axis=1) # 获取除离散化特征之外的其他特征。 X_train_dis = pd.concat([X_train_dis, r], axis=1) # 将离散化后的特征与其他特征进行重新组合。 # 对测试集进行同样的离散化操作。 r = pd.DataFrame(k.transform(X_test_eli[discretize]), index=X_test_eli.index) X_test_dis = X_test_eli.drop(discretize, axis=1) X_test_dis = pd.concat([X_test_dis, r], axis=1) print(X_train_dis.head()) # 查看分箱离散化之后的数据。使用分箱离散化之后的训练集再次进行训练，观察是否有改进： lr.fit(X_train_dis, y_train) # 再次使用训练集训练模型 print("训练集R^2：",lr.score(X_train_dis, y_train)) print("测试集R^2：",lr.score(X_test_dis, y_test)) ------------------------------------------------- 训练集R^2： 0.673533202788688 测试集R^2： 0.6570961283642467 从上面可以看出，分箱离散化之后，模型效果有了进一步的提升。 6 、残差图分析、残差图分析残差，就是模型预测值与真实值之间的差异。我们可以绘制残差图，来对回归模型进行评估，残差图的横坐标为预测值，纵坐标为残差值。对于一个好的回归模型，误差应该是随机分配的。因此，残差也应随机分布于中心线附近。如果我们从残差图中找出规律，这意味着模型遗漏了某些能够影响残差的解释信息。 lr = LinearRegression() lr.fit(X_train_dis, y_train) # 使用异常值处理后的数据进行训练 y_hat = lr.predict(X_test_dis) residual = y_hat - y_test.values # 预测值与真实值之间的差异 plt.xlabel("预测值") plt.ylabel(" 残差") plt.axhline(y=0, color="red") sns.scatterplot(x=y_hat, y=residual)

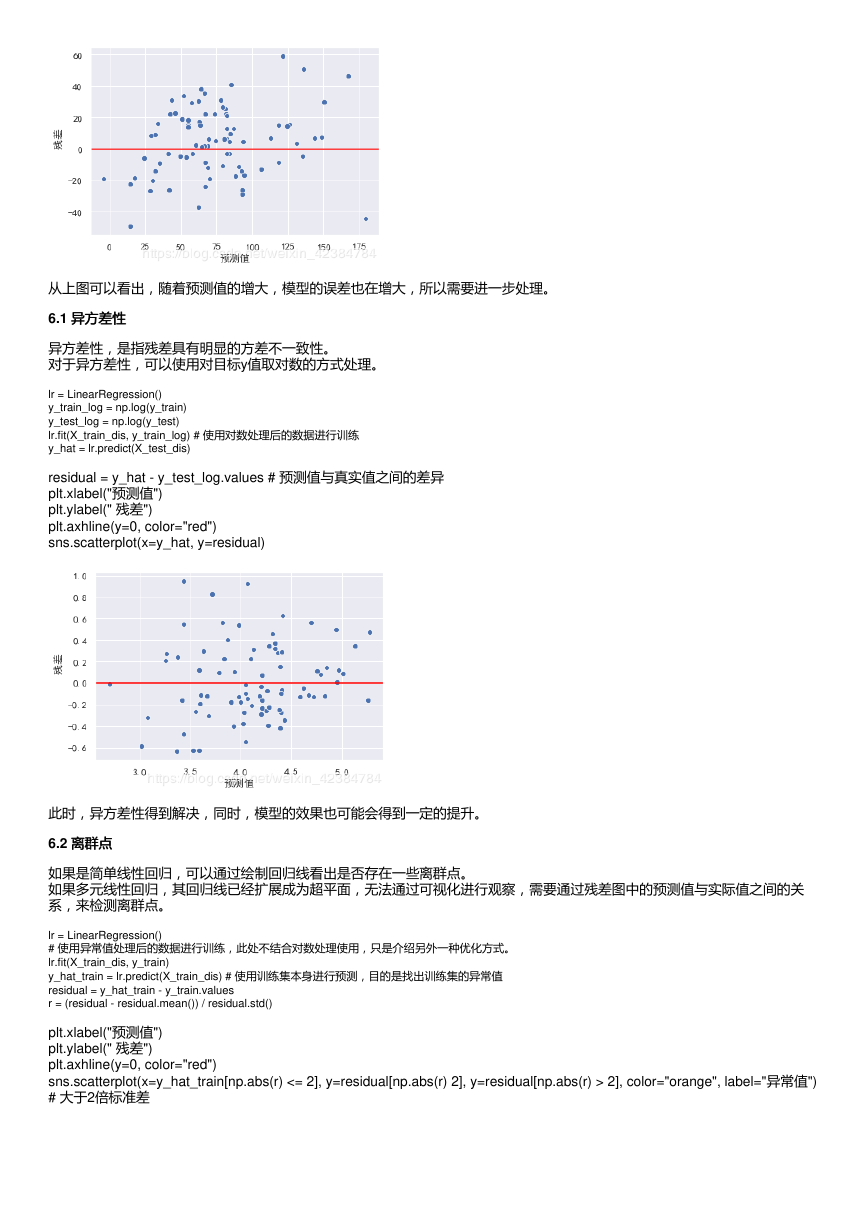
从上图可以看出，随着预测值的增大，模型的误差也在增大，所以需要进一步处理。 6.1 异方差性异方差性异方差性，是指残差具有明显的方差不一致性。对于异方差性，可以使用对目标y值取对数的方式处理。 lr = LinearRegression() y_train_log = np.log(y_train) y_test_log = np.log(y_test) lr.fit(X_train_dis, y_train_log) # 使用对数处理后的数据进行训练 y_hat = lr.predict(X_test_dis) residual = y_hat - y_test_log.values # 预测值与真实值之间的差异 plt.xlabel("预测值") plt.ylabel(" 残差") plt.axhline(y=0, color="red") sns.scatterplot(x=y_hat, y=residual) 此时，异方差性得到解决，同时，模型的效果也可能会得到一定的提升。 6.2 离群点离群点如果是简单线性回归，可以通过绘制回归线看出是否存在一些离群点。如果多元线性回归，其回归线已经扩展成为超平面，无法通过可视化进行观察，需要通过残差图中的预测值与实际值之间的关系，来检测离群点。 lr = LinearRegression() # 使用异常值处理后的数据进行训练，此处不结合对数处理使用，只是介绍另外一种优化方式。 lr.fit(X_train_dis, y_train) y_hat_train = lr.predict(X_train_dis) # 使用训练集本身进行预测，目的是找出训练集的异常值 residual = y_hat_train - y_train.values r = (residual - residual.mean()) / residual.std() plt.xlabel("预测值") plt.ylabel(" 残差") plt.axhline(y=0, color="red") sns.scatterplot(x=y_hat_train[np.abs(r) <= 2], y=residual[np.abs(r) 2], y=residual[np.abs(r) > 2], color="orange", label="异常值") # 大于2倍标准差

去除离群点后，重新进行训练： X_train_dis_filter = X_train_dis[np.abs(r) <= 2] y_train_filter = y_train[np.abs(r) <= 2] lr.fit(X_train_dis_filter, y_train_filter) print(lr.score(X_train_dis_filter, y_train_filter)) print(lr.score(X_test_dis, y_test)) ----------------------------------------- 0.7068375186764522 0.6874497313003948 从以上结果来看，训练效果有了进一步的提升，模型建立完成，后续有未知数据，即可进行AQI的数据。作者：Minions2020

资料库

python数据分析实战之AQI预测.pdf

相关推荐

开发技术

热门标签

最新资料