一种北斗伪距单点定位的整体最小二乘（TLS）算法.pdf-资料库

中国科技论文在线 http://www.paper.edu.cn 一种北斗伪距单点定位的整体最小二乘（TLS）算法马天明1，曾繁慧2** 5 10 （1. 辽宁工程技术大学测绘与地理科学学院，阜新 123000； 2. 辽宁工程技术大学理学院，阜新 123000）摘要：目前，北斗伪距单点定位一般都采用普通最小二乘定位算法，但是,该算法只是考虑了观测方程的常数项的误差，而实际上观测方程的系数矩阵也存在误差，针对这一现象，对北斗伪距单点定位采用整体最小二乘算法，把系数矩阵和常数项的误差都考虑进去，与普通最小二乘算法相比，定位精度更高，应用范围更广。关键词：北斗；伪距单点定位；整体最小二乘中图分类号：P228 15 A pseudo-range singe point positioning algorithm for the Beidou navigation system based on total least squares Ma Tianming1, Zeng Fanhui2 (1. Geomatics School,Liaoning Technical University ,Fuxin 123000; 2. Science School,Liaoning Technical University,Fuxin 123000) 20 25 Abstract: At present,BDS pseudo-range single point positioning is generally used oridinary least squares,however,the algorithm is only considered the error of constant term,in fact,coefficient matrix of observation equation is also contained error,for this phenomenon,using total least squares algorithm for BDS pseudo-range single point positioning,the error of the coefficient matrix and the constant term is considered,compared with ordinary least squares algorithm,higher accuracy and wider application. Key words: GNSS;single point positioning;Least Squares Algorithm 0 引言在 2012 年 10 月 25 日，我国北斗卫星系统发射了第十六颗导航卫星，这极大地促进了 30 我国以及周边国家的导航事业的发展。而北斗伪距单点定位因其速度快、灵活方便、只需要一台接收机就能满足实时测量的要求，被广泛的应用于车辆、船舶、飞机导航，地质勘测以及海洋捕鱼等领域[1]。所以提高北斗伪距单点定位的精度对我国加速北斗产业化步伐起到重要的推动作用。 35 40 北斗伪距单点定位是以北斗卫星和用户接收机天线间的距离观测量为基础，并根据卫星坐标来确定接收机天线所对应的观测点的坐标[2]，本文运用整体最小二乘算法和普通最小二乘算法，在VS2010 软件平台上，通过编写C++程序语言实现了北斗卫星系统的伪距单点定位，由于北斗伪距单点定位忽略电离层、对流层、测量噪声等对定位精度的影响[3]，所以其定位精度相较于精密单点定位略差，运用普通最小二乘算法的定位精度在10m左右，而运用整体最小二乘算法进行定位计算，相较于普通最小二乘，定位精度在平面位置可以提高4m 左右，在垂直方向可以提高2m左右，而且运用整体最小二乘算法可以加快坐标收敛速度，加快用户的定位速度。作者简介：马天明（1989-），男，硕士，研究方向：大地测量通信联系人：曾繁慧，女，教授，主要研究方向：信息科学与应用. E-mail: 597873883@qq.com - 1 -

中国科技论文在线 1 整体最小二乘的基本思想 http://www.paper.edu.cn 45 50 55 对于线性方程组 AX=L普通最小二乘的基本思想是在残差平方和极小的准则约束下求解最佳参数。这里有一个前提，系数矩阵A是没有误差的精确值但是多数情况系数阵A和观测向量L同时存在误差，若同时考虑二者的误差，此时，线性方程组可表示为[4] (1-1) 为系数阵的噪声，为观测噪声，误差矩阵属于相互独立的自噪声误差。这一模型称为 EIV（Errors-in-Variables）模型，解决这类问题的适宜方法是整体最小二乘法（Total Least Squares, TLS），对于线性方程组 AX=L 整体最小二乘问题就是在以下准则约束下寻求和， (1-2) 任何满足 X= 的 X 均称为线性方程 AX=L 的整体最小二乘解。式中范数，简称为 F 范数。为 Frobenius 2 整体最小二乘应用于北斗伪距单点定位 60 北斗伪距单点定位的原理就是通过接收机接受 4 颗及 4 颗以上的导航电文和卫星星历数据，利用卫星导航电文和卫星星历数据解算出卫星的位置，再利用卫星与用户间的空间几何关系构造方程求解[5]。若为伪距观测值，VR 为接收机钟差，VS 为卫星钟差，Vion 为电离层延迟，Vtrop 为对流层延迟,北斗伪距单点定位的观测方程如式 2-1 所示， 65 (2-1) 若测站的近似坐标为（X0，Y0，Z0），将上式在（X0，Y0，Z0）处用泰勒级数展开后可得线性化的观测方程如式 2-2 所示[6]： 70 (2-2) 式中，为测站近似位置至第 i 颗卫星的距离，为从测站的近似位置至卫星 i 方向上的方向余弦，于是误差方程可以写成式 2-3 的形式： 75 (2-3) 式中的常数项为： (2-4) 80 误差方程的矩阵形式为： - 2 - LAELXEA)(AELELAEE,ALFLALA||],[],[||minALFM||||iitropiionSRiiiiVVCVcVzzyyxx)()()()()(222itropiionSRzyxVVcVcVVzzVyyVxxiiiiiiii)()()()()(00000000i,,,000000)()()(iiinzzmyylxxiiiiiiiRziyixiiLcVVnVmVlVitropiionSiiVVcVLi)()(0

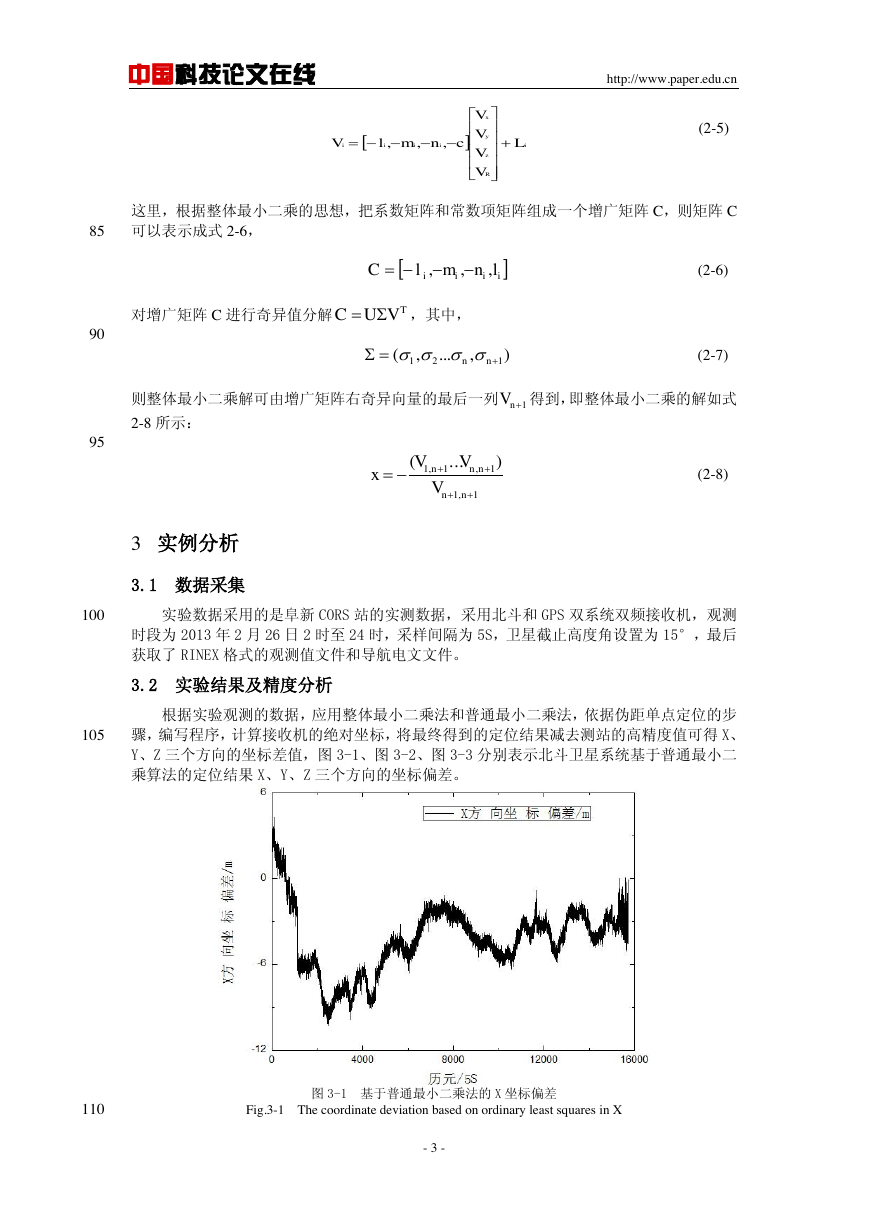
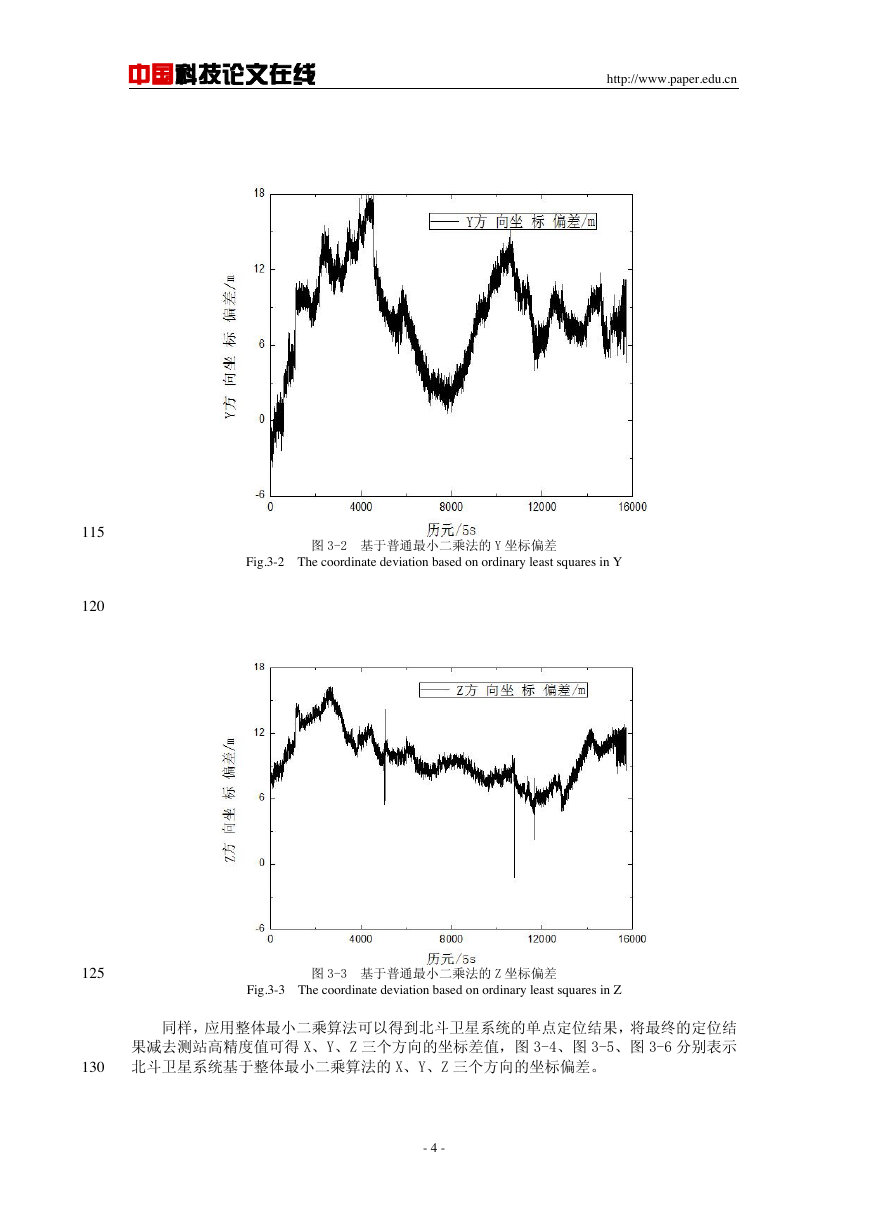
中国科技论文在线 http://www.paper.edu.cn (2-5) 这里，根据整体最小二乘的思想，把系数矩阵和常数项矩阵组成一个增广矩阵 C，则矩阵 C 可以表示成式 2-6， (2-6) (2-7) 得到，即整体最小二乘的解如式 (2-8) 85 90 对增广矩阵 C 进行奇异值分解，其中，则整体最小二乘解可由增广矩阵右奇异向量的最后一列 2-8 所示： 95 3 实例分析 3.1 数据采集 100 实验数据采用的是阜新 CORS 站的实测数据，采用北斗和 GPS 双系统双频接收机，观测时段为 2013 年 2 月 26 日 2 时至 24 时，采样间隔为 5S，卫星截止高度角设置为 15°，最后获取了 RINEX 格式的观测值文件和导航电文文件。 3.2 实验结果及精度分析根据实验观测的数据，应用整体最小二乘法和普通最小二乘法，依据伪距单点定位的步 105 骤，编写程序，计算接收机的绝对坐标，将最终得到的定位结果减去测站的高精度值可得 X、 Y、Z 三个方向的坐标差值，图 3-1、图 3-2、图 3-3 分别表示北斗卫星系统基于普通最小二乘算法的定位结果 X、Y、Z 三个方向的坐标偏差。 110 Fig.3-1 The coordinate deviation based on ordinary least squares in X 图 3-1 基于普通最小二乘法的 X 坐标偏差 - 3 - iRzyxiiiiLVVVVcnmlV,,,iiiilnmlC,,,TVUC),...,(121nn1nV1,11,1,1)...(nnnnnVVVx

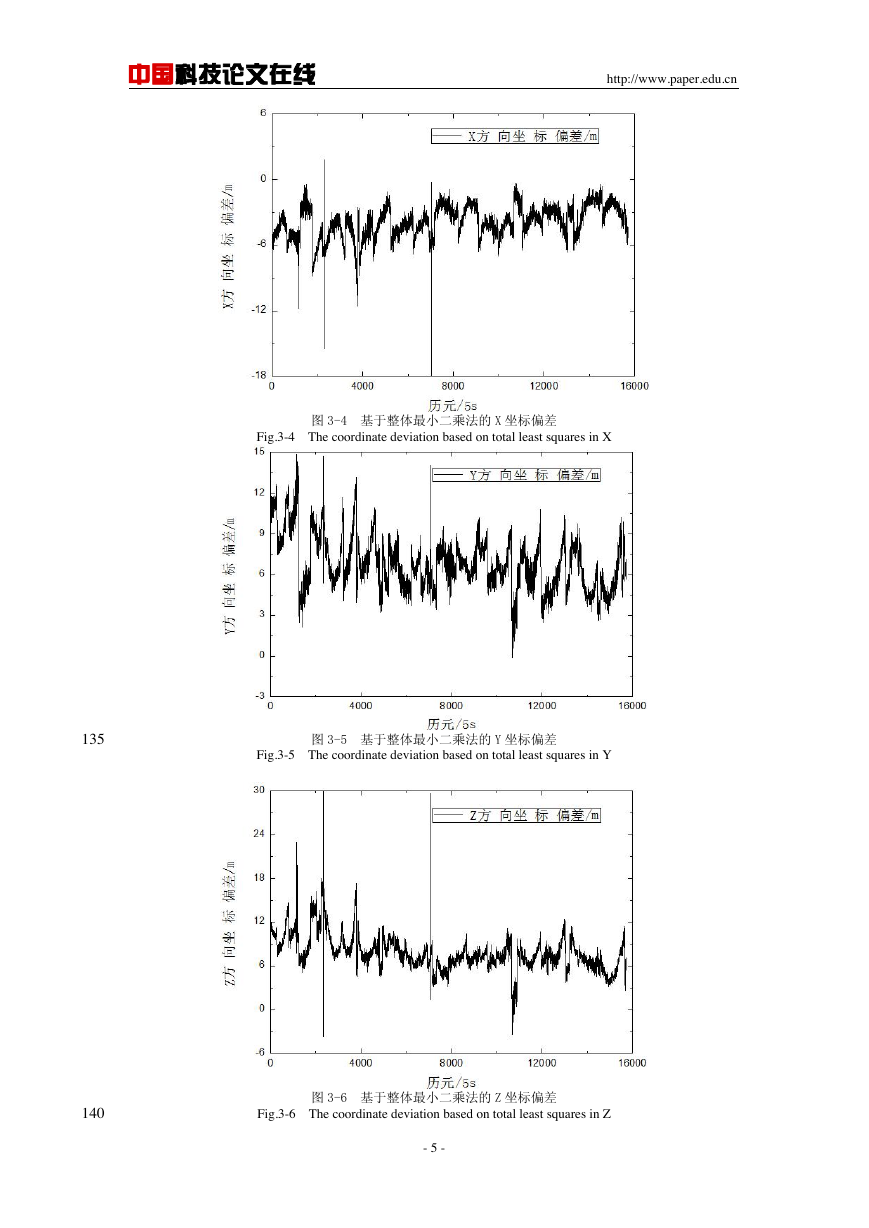
中国科技论文在线 http://www.paper.edu.cn 115 120 125 130 图 3-2 基于普通最小二乘法的 Y 坐标偏差 Fig.3-2 The coordinate deviation based on ordinary least squares in Y 图 3-3 基于普通最小二乘法的 Z 坐标偏差 Fig.3-3 The coordinate deviation based on ordinary least squares in Z 同样，应用整体最小二乘算法可以得到北斗卫星系统的单点定位结果，将最终的定位结果减去测站高精度值可得 X、Y、Z 三个方向的坐标差值，图 3-4、图 3-5、图 3-6 分别表示北斗卫星系统基于整体最小二乘算法的 X、Y、Z 三个方向的坐标偏差。 - 4 -

中国科技论文在线 http://www.paper.edu.cn 图 3-4 基于整体最小二乘法的 X 坐标偏差 Fig.3-4 The coordinate deviation based on total least squares in X 135 图 3-5 基于整体最小二乘法的 Y 坐标偏差 Fig.3-5 The coordinate deviation based on total least squares in Y 140 图 3-6 基于整体最小二乘法的 Z 坐标偏差 Fig.3-6 The coordinate deviation based on total least squares in Z - 5 -

中国科技论文在线 http://www.paper.edu.cn 从图 3-1 至图 3-6 可以看出，基于普通最小二乘算法的北斗伪距单点定位结果的 X、Y、 Z 三个方向的坐标偏差都在 10m 左右，而且定位结果不稳定，而应用整体最小二乘算法的北斗北斗伪距单点定位结果的坐标偏差在 5m 左右，即整体最小二乘算法较普通最小二乘算法的定位精度要高 5m 左右，而且除个别历元外，整体最小二乘算法的定位结果相对更稳定，结果更可靠。 4 结论本文将整体最小二乘法应用于北斗的伪距单点定位的计算中，用 C++语言实现了北斗卫星系统的伪距单点定位，通过与普通最小二乘法的定位结果对比，可以看出，基于普通最小二乘算法的北斗伪距单点定位结果的 X、Y、Z 三个方向的坐标偏差都在 10m 左右，而且定位结果不稳定，而应用整体最小二乘算法的北斗北斗伪距单点定位结果的坐标偏差在 5m 左右，即整体最小二乘算法较普通最小二乘算法的定位精度要高 5m 左右，这样可以为单点定位用户提供精度更高的绝对定位结果。 [参考文献] (References) [1] 裴霄，王解先. GPS 伪距单点定位的精度分析及改进[J].海洋测绘.2012，32（1）：5-7. [2] 李征航，黄劲松.GPS 测量与数据处理[M].武汉：武汉大学出版社，2005. [3] 张月超，陈义等.Kalman 滤波在 GNSS 伪距单点定位中的应用[J].全球定位系统.2013，38（6）：31-35. [4] 丁克良,欧吉坤,陈义.整体最小二乘法及其在测量数据处理中的应用[Z].北京：中国测绘学会，2009. [5] 安向东.GPS 与北斗伪距单点定位性能对比分析[J].全球定位系统.2014，39（3）：8-14. [6] 陈希孺.最小二乘法的历史回顾与现状[J].中国科学院研究生院学报.1998，15（1）：4-11. 145 150 155 160 - 6 -

资料库

一种北斗伪距单点定位的整体最小二乘（TLS）算法.pdf

相关推荐

开发技术

热门标签

最新资料