第1页 / 共15页
第2页 / 共15页
第3页 / 共15页
第4页 / 共15页
第5页 / 共15页
第6页 / 共15页
第7页 / 共15页
第8页 / 共15页
abaqus动刚度.pdf
无标题
F(ω)=F0×sin(ωt) 输入激励力
当使用 abaqus-steady-state daynmics modal，
其中 20-1000 即为激励力的最低频率和最高频率。
开始模态和结束模态 要覆盖上图所示的激励力的最低频率和最
高频率，选择直接阻尼，即每阶模态的临界阻尼比 3%，（典型的取值
范围在 1%-10%）
Ma+cv+kx= F0×sin(ωt)
其中 F0 是固定的数值（简谐力的幅值），且频率由 20Hz 变化到
1000Hz。
•= πω 2
f•
位移阻抗（动刚度）： (
K
)
ω
=
(
)
F
ω
(
)ω
x
(
)
ω
F
=
F
0 •
sin
(
)t
ω
为输入激励力，是一个谐波输入。
(
)
ω
x
=
x
0
•
sin
(
)θω
t
+
为输出稳态位移响应，根据振动理论，稳态位
移响应的频率与输入激励力的频率相同，振幅
0x 和相位角θ均取决
与系统本身的物理性质（质量，弹簧刚度，阻尼）和激振力的性质（频
率与振幅），而与初始条件无关，初始条件仅影响系统的瞬态响应的
振幅和初始相位角。
)ωK ，表示，在某频率下，产生单位位移振幅所需要的激振力幅
(
值。实际情况下，频率不同，刚度也不同。
假设 (
)ωK
=10N/m，及动刚度在任意频率都是固定的，不随频率
的变化而变化（理想情况），即在任意频率激振下，产生 1m 单位位
移振幅所需要的激振力幅值为 10N。
假设 (
)ωF 的幅值为 1 ， (
)ωK
=10N/m
)
)ωx 的幅值x= (
F
ω
(
(
)ω
K
=
1 特点：位移响应的幅值与频率没有关
10
系，且是固定值。
由于在 abaqus 中可方便的输出某个点的位移，速度，加速度。
所以通常以某个点的位移，速度，加速度来表征动刚度的大小。
速度阻抗： (
Z
)
)
(
F
ω
ω •=
(
)ω
x
如何将速度阻抗： (
Z
)
(
)
F
ω
与位移阻抗（动刚度）： (
K
ω •=
(
)ω
x
)
ω
=
(
)
F
ω
(
)ω
x
联系起来？
用速度表示：
•
x
(
)ω
=
)ωx 的导数=
(
x
0
=
x
0
•
)'
θωω
sin
+
•
(
t
•
的导数
(
)θω +
t
sin
=
)ωω x• （我们只要幅值，忽略相位角）
(
响应速度与响应位移幅值相差ω，相位角不同，频率相同。
(
)
ω
x
=
(
)
ω
)ω
(
F
K
•
x
)ω
(
=
)ωω x•
(
=
ω
F•
K
(
)
ω
)ω
(
假设 (
)ωF 的幅值为 1 ， (
=10N/m（不随频率的变化而变化）
则 (
•
)ω
x 的幅值
•
x=
ω
•
K
1
)
(
ω
2
fπ
•×
•
1
10
)ωK
1•ω =
=
10
••
x=
ωω
•
•
1
)
(
ω
K
•ωω
=
1•
10
=
2
π
•×
f
2
π
•×•
f
•
1
10
同理
••
(
)ω
x 的幅值
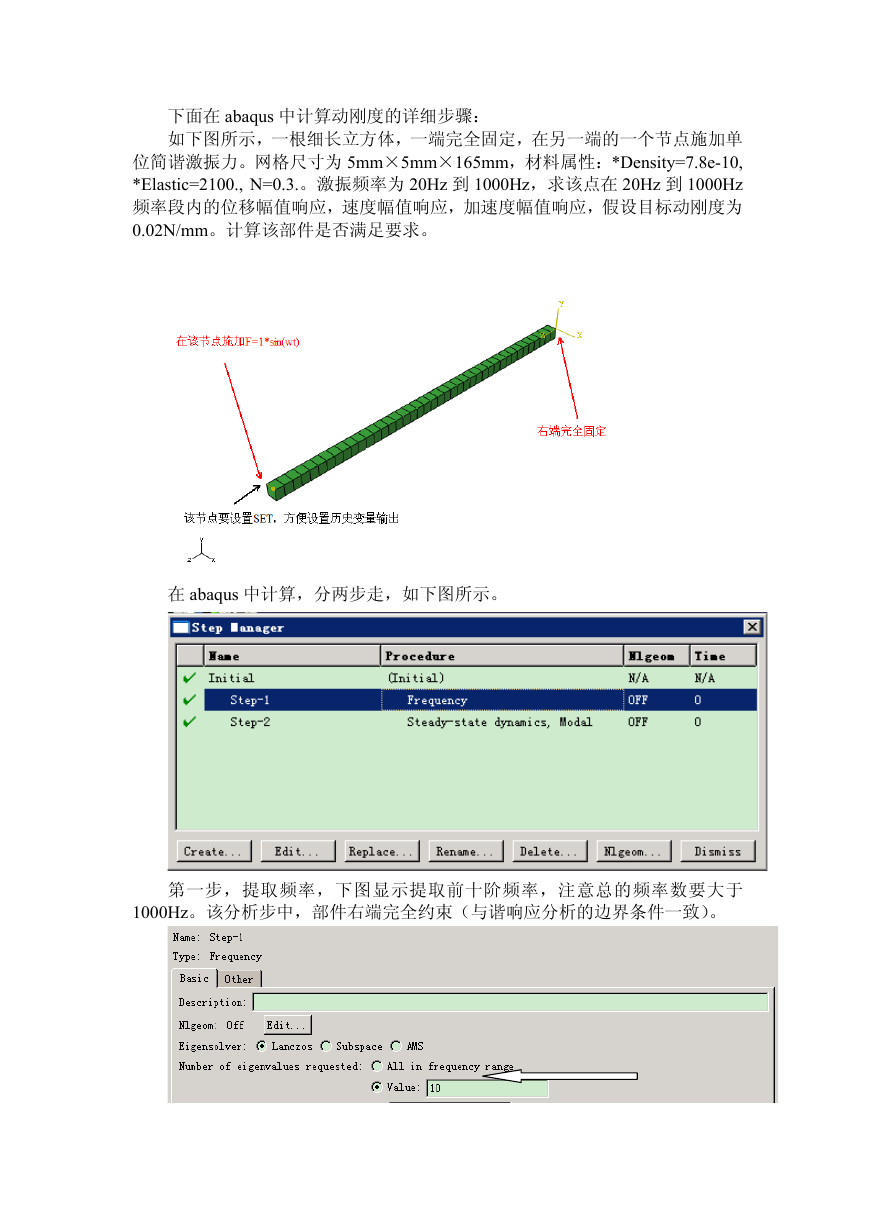
下面在 abaqus 中计算动刚度的详细步骤：
如下图所示，一根细长立方体，一端完全固定，在另一端的一个节点施加单
位简谐激振力。网格尺寸为 5mm×5mm×165mm，材料属性：*Density=7.8e-10,
*Elastic=2100., N=0.3.。激振频率为 20Hz 到 1000Hz，求该点在 20Hz 到 1000Hz
频率段内的位移幅值响应，速度幅值响应，加速度幅值响应，假设目标动刚度为
0.02N/mm。计算该部件是否满足要求。
在 abaqus 中计算，分两步走，如下图所示。
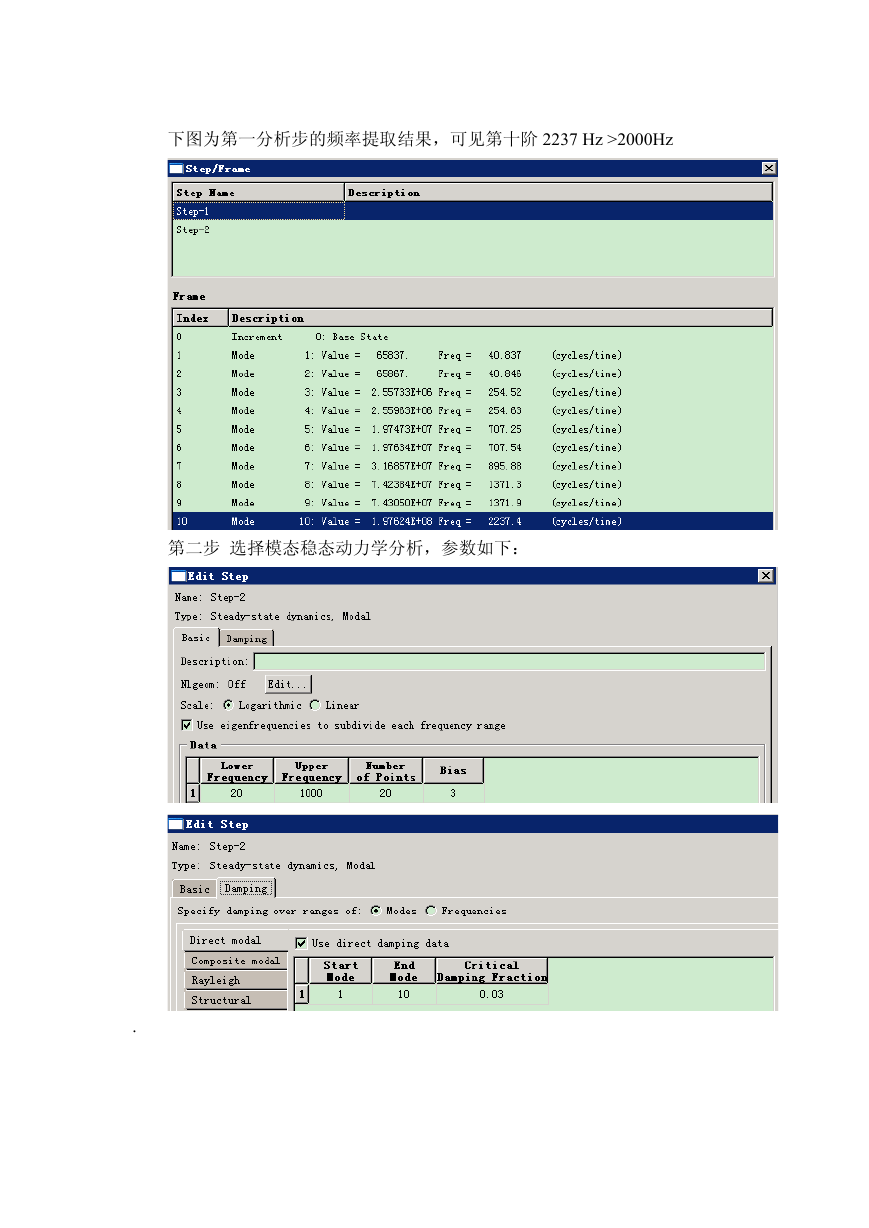
第一步，提取频率，下图显示提取前十阶频率，注意总的频率数要大于
1000Hz。该分析步中，部件右端完全约束（与谐响应分析的边界条件一致）。
下图为第一分析步的频率提取结果，可见第十阶 2237 Hz >2000Hz
第二步 选择模态稳态动力学分析，参数如下：
.
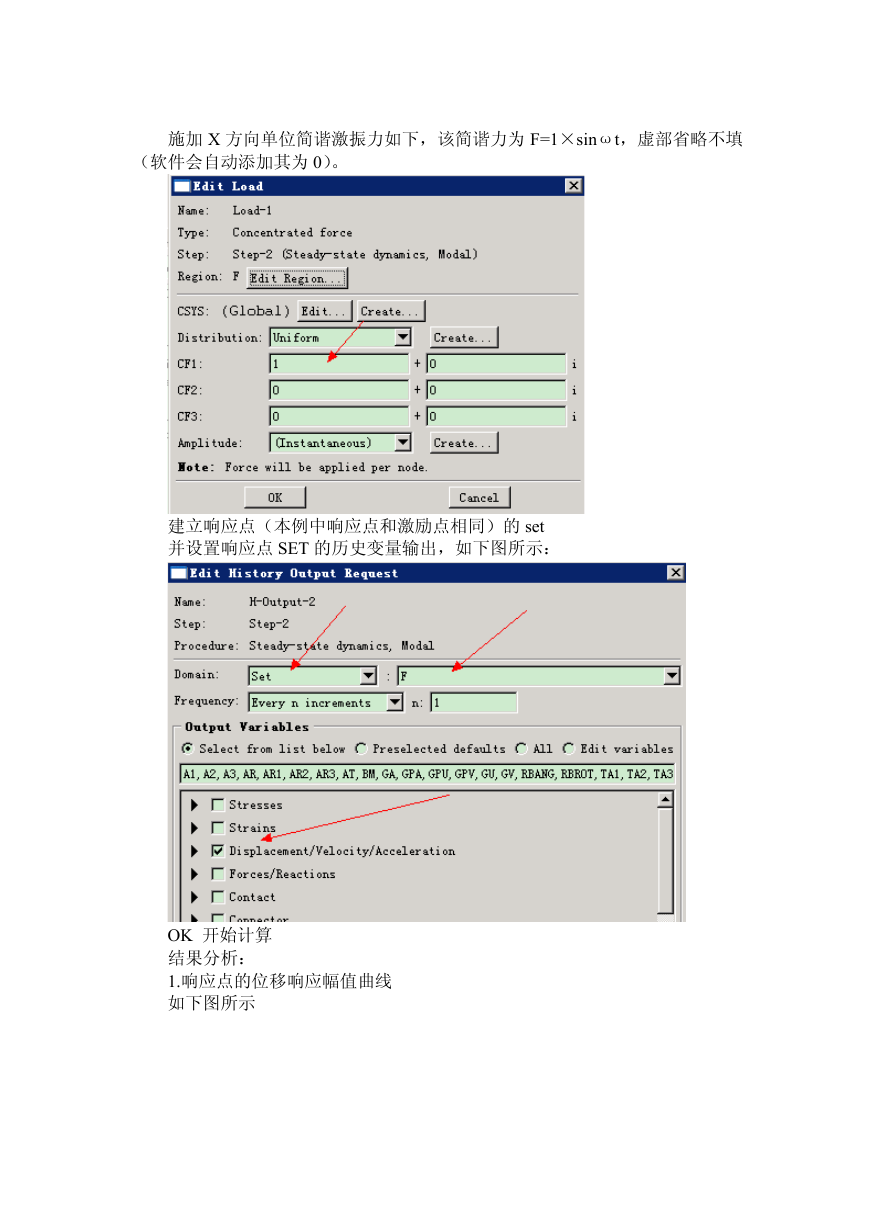
施加 X 方向单位简谐激振力如下，该简谐力为 F=1×sinωt，虚部省略不填
（软件会自动添加其为 0）。
建立响应点（本例中响应点和激励点相同）的 set
并设置响应点 SET 的历史变量输出，如下图所示：
OK 开始计算
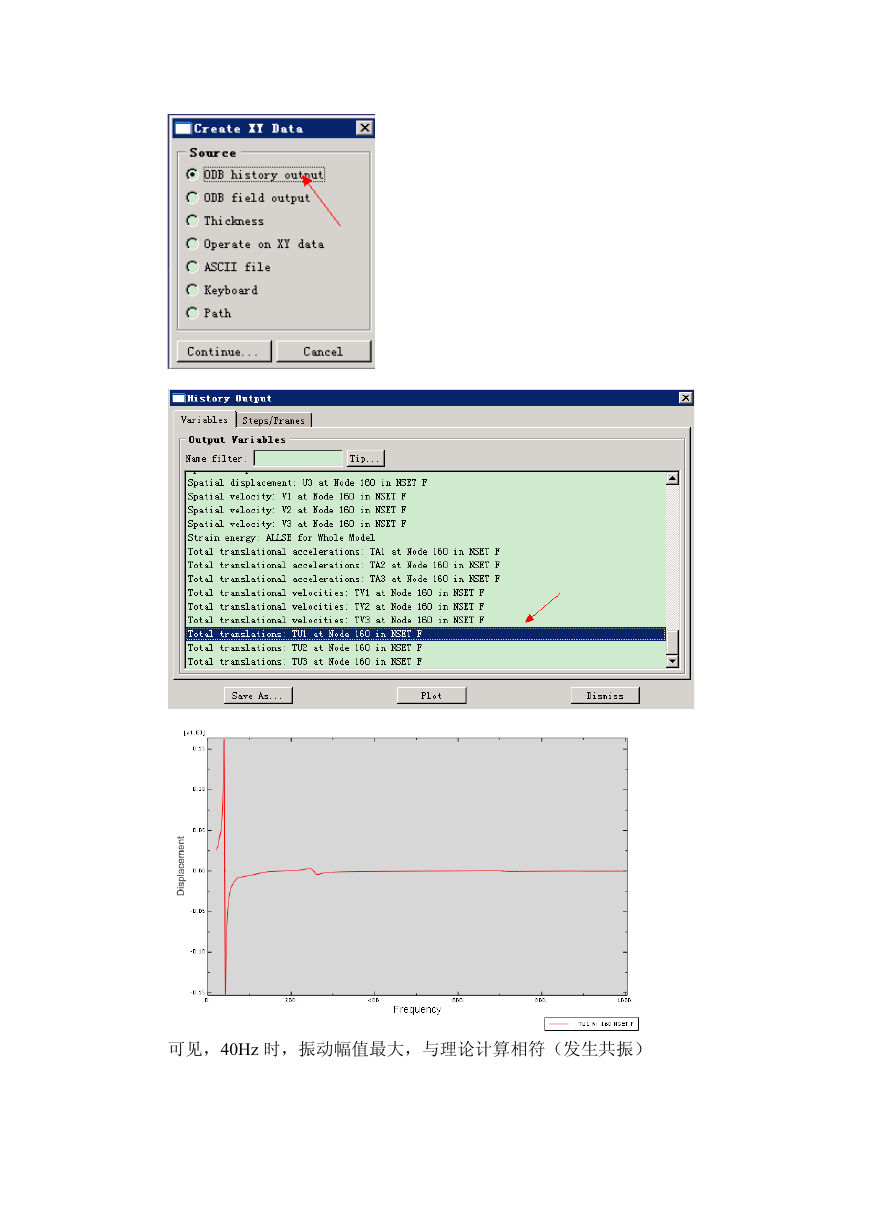
结果分析：
1.响应点的位移响应幅值曲线
如下图所示
可见，40Hz 时，振动幅值最大，与理论计算相符（发生共振）
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
