率失真模型与量化讲解.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书资料大小：1.60M 资料格式：pdf 举报版权申诉

m7zone-2144158-16359647630648414097.pdf-第1页.png

第1页 / 共33页

m7zone-2144158-16359647630648414097.pdf-第2页.png

第2页 / 共33页

m7zone-2144158-16359647630648414097.pdf-第3页.png

第3页 / 共33页

m7zone-2144158-16359647630648414097.pdf-第4页.png

第4页 / 共33页

m7zone-2144158-16359647630648414097.pdf-第5页.png

第5页 / 共33页

m7zone-2144158-16359647630648414097.pdf-第6页.png

第6页 / 共33页

m7zone-2144158-16359647630648414097.pdf-第7页.png

第7页 / 共33页

m7zone-2144158-16359647630648414097.pdf-第8页.png

第8页 / 共33页

文本预览

Rate Distortion Theory & Quantization Rate Distortion Theory & Quantization Rate Distortion Theory Rate Distortion Function for Memoryless Gaussian Sources for Gaussian Sources with Memory R(D*) R(D*) Scalar Quantization Lloyd-Max Quantizer High Resolution Approximations Entropy-Constrained Quantization Vector Quantization Thomas Wiegand: Digital Image Communication RD Theory and Quantization 1

Rate Distortion Theory Rate Distortion Theory Theoretical discipline treating data compression from the viewpoint of information theory. Results of rate distortion theory are obtained without consideration of a specific coding method. Goal: Rate distortion theory calculates minimum transmission bit-rate for a given distortion and source. R D Thomas Wiegand: Digital Image Communication RD Theory and Quantization 2

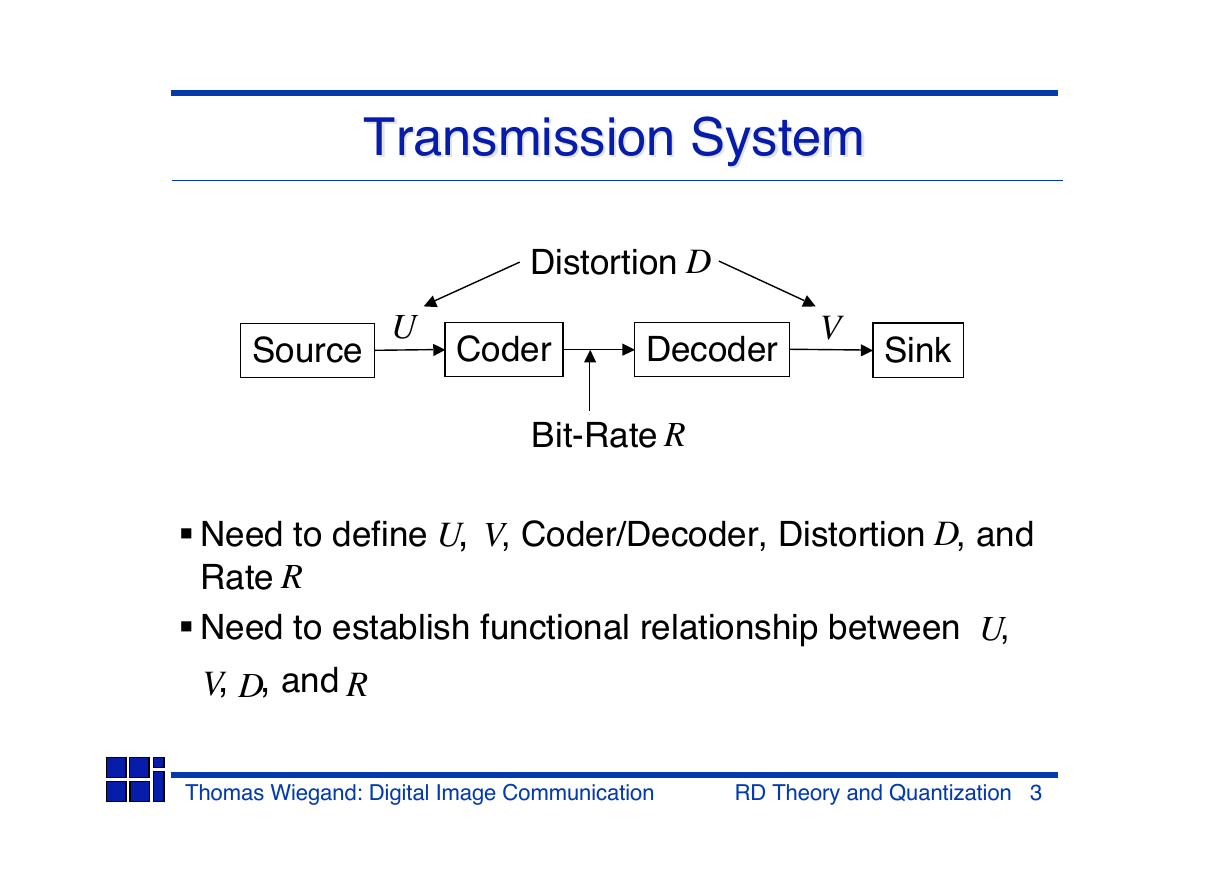
Transmission System Transmission System Distortion D U Source Coder Decoder V Sink Bit-Rate R Need to define , , Coder/Decoder, Distortion , and U V D Rate R U Need to establish functional relationship between , , , and V D R Thomas Wiegand: Digital Image Communication RD Theory and Quantization 3

Definitions Definitions Source symbols are given by the random sequence • Each assumes values in the discrete set Uk - For a binary source: - For a picture: U = {0,1} U = {0,1,...,255} {Uk} = {u0,u1,...,uM 1} • For simplicity, let us assume to be independent and identically distributed (i.i.d.) with distribution {P(u),u U} Uk Reconstruction symbols are given by the random sequence {Vk} with distribution {P(v),v } • Each assumes values in the discrete set • The sets and need not to be the same Vk = {v0,v1,...,vN 1} Thomas Wiegand: Digital Image Communication RD Theory and Quantization 4

Coder / Decoder Coder / Decoder Statistical description of Coder/Decoder, i.e. the mapping of the source symbols to the reconstruction symbols, via Q = {Q(v | u),u ,v } is the conditional probability distribution over the letters of the reconstruction alphabet given a letter of the source alphabet Transmission system is described via Joint pdf: P(u,v) P(u) = P(v) = P(u,v) P(u,v) v u P(u,v) = P(u) Q(v | u) (Bayes‘ rule) Thomas Wiegand: Digital Image Communication RD Theory and Quantization 5

Distortion Distortion To determine distortion, we define a non-negative cost function d(u,v),d(.,.) : [0,) Examples for d • Hamming distance: d(u,v) = 0, 1, for u v for u = v • Squared error: d(u,v) = u v 2 Average Distortion D(Q) = P(u) Q(v | u) 1 2 4 4 3 4 4 d(u,v) u v P(u,v) Thomas Wiegand: Digital Image Communication RD Theory and Quantization 6

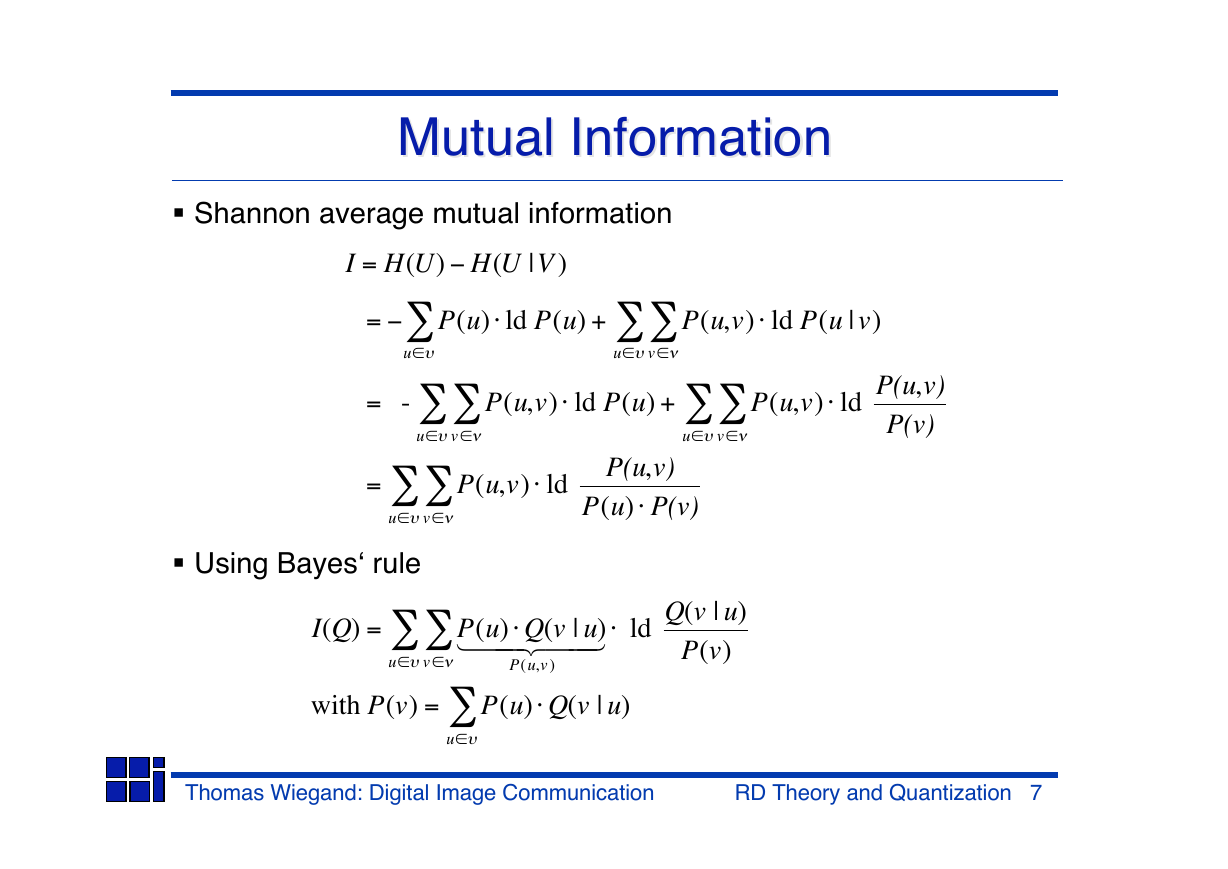
Mutual Information Mutual Information Shannon average mutual information I = H(U) H(U |V ) P(u) ld P(u) + = u u v P(u,v) ld P(u | v) = - u v P(u,v) ld P(u) + P(u,v) ld u v P(u,v) P(v) = u v P(u,v) ld P(u,v) P(u) P(v) Using Bayes‘ rule I(Q) = u v P(u) Q(v | u) 1 2 4 4 3 4 4 ld P(u,v ) Q(v | u) P(v) with P(v) = u P(u) Q(v | u) Thomas Wiegand: Digital Image Communication RD Theory and Quantization 7

RateRate Shannon average mutual information expressed via entropy I(U;V ) = H(U) H(U |V ) Source entropy Equivocation: conditional entropy Equivocation: • The conditional entropy (uncertainty) about the source given the reconstruction U V • A measure for the amount of missing [quantized] information in the received signal V Thomas Wiegand: Digital Image Communication RD Theory and Quantization 8

分享到：

赞收藏

资料库

率失真模型与量化讲解.pdf

相关推荐

课程资源

热门标签

最新资料