用matlab解信号处理系统微分方程.docx

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.22M 资料格式：docx 举报版权申诉

wutao22-2855908-4744302542899207788.docx.pdf-第1页.png

第1页 / 共7页

wutao22-2855908-4744302542899207788.docx.pdf-第2页.png

第2页 / 共7页

wutao22-2855908-4744302542899207788.docx.pdf-第3页.png

第3页 / 共7页

wutao22-2855908-4744302542899207788.docx.pdf-第4页.png

第4页 / 共7页

wutao22-2855908-4744302542899207788.docx.pdf-第5页.png

第5页 / 共7页

wutao22-2855908-4744302542899207788.docx.pdf-第6页.png

第6页 / 共7页

wutao22-2855908-4744302542899207788.docx.pdf-第7页.png

第7页 / 共7页

文本预览

Matlab 期末考试班级：2007 级电科一班姓名：吴涛学号：20074053053 已知微分方程： ( ) d y t 2 2 dt  7 ( ) dy t dt  10 ( ) y t  2 ( ) d e t 2 dx  6 ( ) de t dt  4 ( ) e t 1. 用 M 语言编程，求冲击响应，阶跃响应，并绘制图形，注上对应的连续解 2. 使用 simulink 工具箱，求其在幅值为 1，周期为 1s，5s，10s 的方波作用下的响应，在同一张图形中绘制激励与响应图形一、用 M 语言编程求下面微分方程的冲击响应和阶跃响应 ( ) de t dt 2 ( ) d e t 2 dx ( ) d y t 2 ( ) dy t dt 10 ( ) y t 2 dt 6    7   4 ( ) e t 1. 建模：线性常微分方程的解一般可以用拉普拉斯算子 s 表示 Y(s)=B(s)/A(s) 其中 B(s)和 A(s)都是 s 的多项式，分母多项式的次数 n 通常高于分子多项式的次数 m。在时间域的解 y(t)是 Y(s)的拉普拉斯的反变换。求反变换的重要方法之一就是部分分式法，即将上述多项式分解为多个 s 的一次分式之和。留数函数 residue 可以完成这一任务。步骤： (1)用[r,p,k]=residue(b,a),求出 Y(s)的极点数组 p 和留数数组（设分母比分子的阶数高，故 k=0）因而 Y(s)可以表示为 (1) s  r  ( ) Y s (1) p (2)求它的反变换，得 y(t)=r(1)*exp(p(1)*t)+ r(4)*exp(p(4)*t)+.........  r  (2) p (2) s  r  (3) p (3) s  ....... r(2)*exp(p(2)*t)+ r(3)*exp(p(3)*t)+ 2. 求阶跃响应的程序 clear;close all t=0:0.2:10 a=[1,7,10,0];b=[1,6,4];[r,p,k]=residue(b,a)

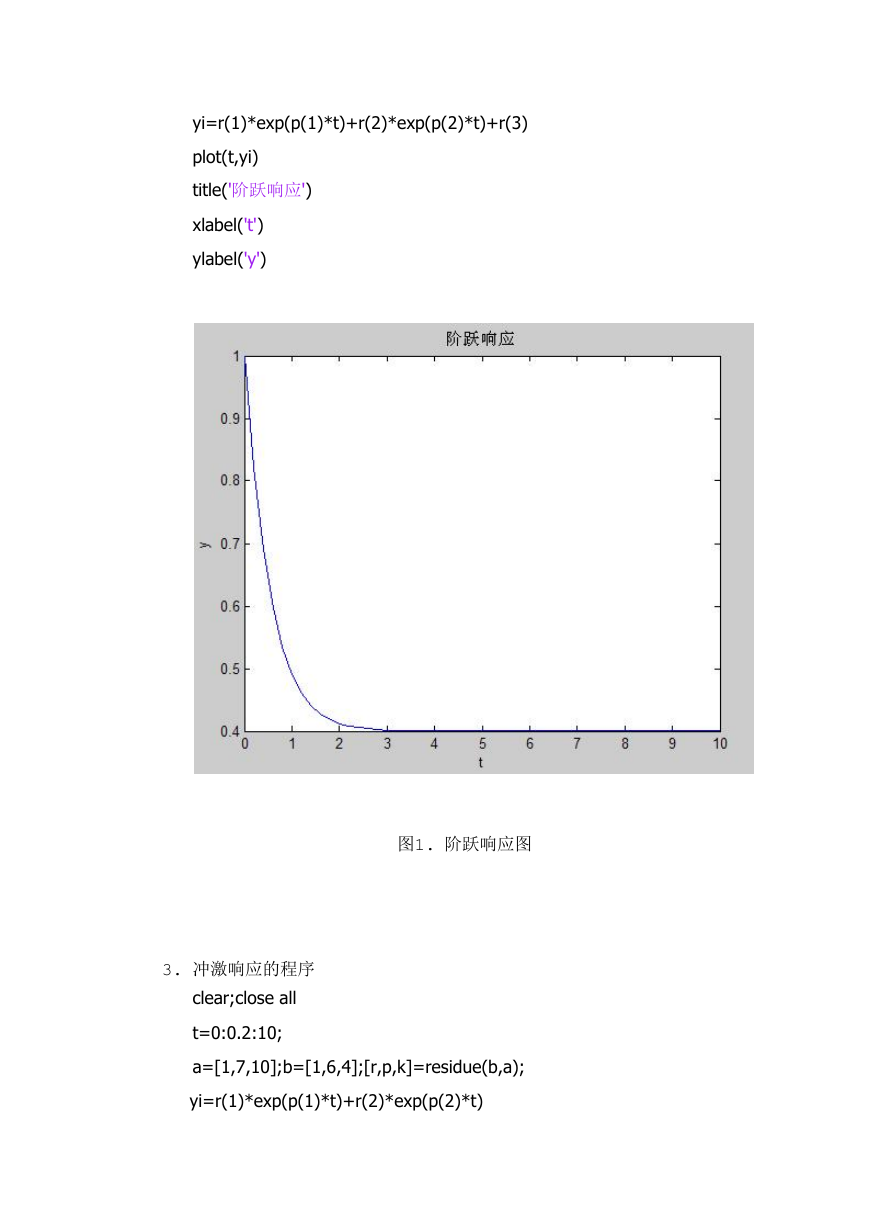
yi=r(1)*exp(p(1)*t)+r(2)*exp(p(2)*t)+r(3) plot(t,yi) title('阶跃响应') xlabel('t') ylabel('y') 图1. 阶跃响应图 3. 冲激响应的程序 clear;close all t=0:0.2:10; a=[1,7,10];b=[1,6,4];[r,p,k]=residue(b,a); yi=r(1)*exp(p(1)*t)+r(2)*exp(p(2)*t)

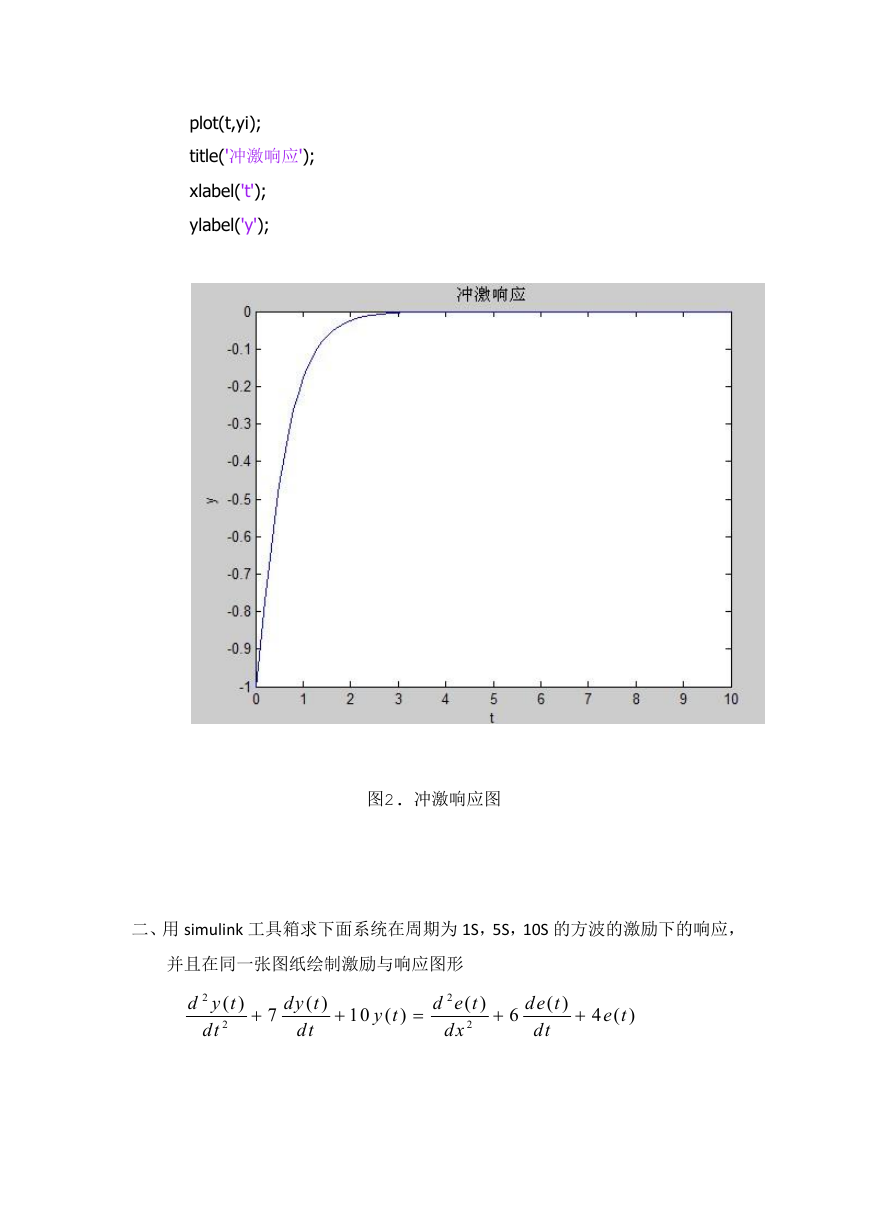
plot(t,yi); title('冲激响应'); xlabel('t'); ylabel('y'); 图2. 冲激响应图二、用 simulink 工具箱求下面系统在周期为 1S，5S，10S 的方波的激励下的响应，并且在同一张图纸绘制激励与响应图形 ( ) d y t 2 2 dt  7 ( ) dy t dt  10 ( ) y t  2 ( ) d e t 2 dx  6 ( ) de t dt  4 ( ) e t

1、分析建模与上面用 M 语言编程的方法一样，用 simulink 建模的思想也是通过拉普拉斯变换，然后用相应的 BLOCK 进行模型搭建，在此系统中用到的 BLOCK 有 Transfer fcn、Pulse Generator、mux、Scope，搭建好模型好，通过修改参数可以达到系统的要求： 2、各个 BLOCK 的参数设置 2.1、Transfer fcn 分子系数的行向量。具有多个行矩阵可以指定生成多个输出默认值是[1]，根据系统的要求要改成[1 6 4] Transfer fcn 分母系数的行向量。默认为[1 1],根据系统要求改成[1 7 10] 图 1. Transfer Fcn 的参数设置

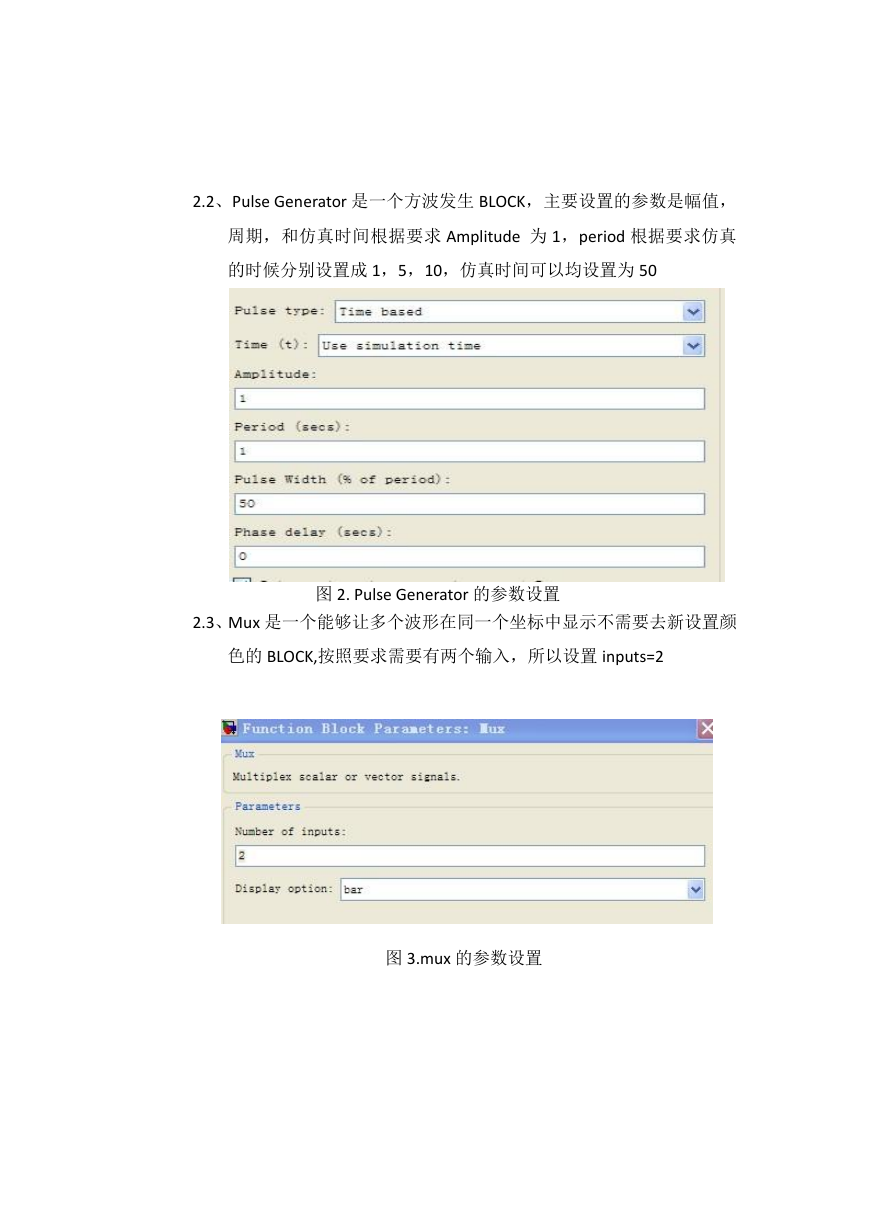
2.2、Pulse Generator 是一个方波发生 BLOCK，主要设置的参数是幅值，周期，和仿真时间根据要求 Amplitude 为 1，period 根据要求仿真的时候分别设置成 1，5，10，仿真时间可以均设置为 50 图 2. Pulse Generator 的参数设置 2.3、Mux 是一个能够让多个波形在同一个坐标中显示不需要去新设置颜色的 BLOCK,按照要求需要有两个输入，所以设置 inputs=2 图 3.mux 的参数设置

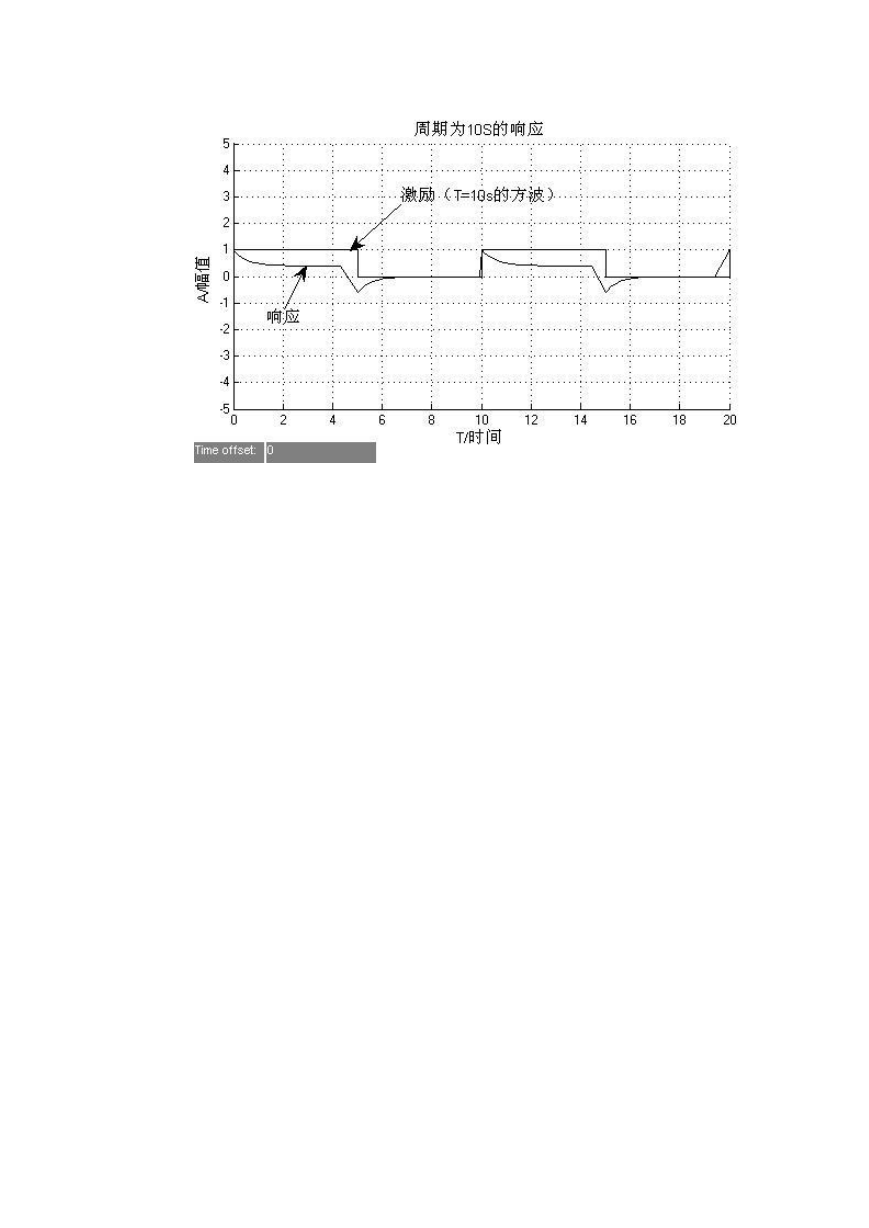
2.4、3 个不同周期作为激励和相应的响应仿真图

分享到：

赞收藏

资料库

用matlab解信号处理系统微分方程.docx

相关推荐

开发技术

热门标签

最新资料