经典matlab拓扑优化程序.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：1.32M 资料格式：pdf 举报版权申诉

solowmq-2878387-16359647578171752062.pdf-第1页.png

第1页 / 共14页

solowmq-2878387-16359647578171752062.pdf-第2页.png

第2页 / 共14页

solowmq-2878387-16359647578171752062.pdf-第3页.png

第3页 / 共14页

solowmq-2878387-16359647578171752062.pdf-第4页.png

第4页 / 共14页

solowmq-2878387-16359647578171752062.pdf-第5页.png

第5页 / 共14页

solowmq-2878387-16359647578171752062.pdf-第6页.png

第6页 / 共14页

solowmq-2878387-16359647578171752062.pdf-第7页.png

第7页 / 共14页

solowmq-2878387-16359647578171752062.pdf-第8页.png

第8页 / 共14页

Combination of quantum mechanics and topology optimization

Outlines

Topology optimization and the Schrodinger equation

幻灯片编号 4

幻灯片编号 5

Quantum well solar cells

幻灯片编号 7

幻灯片编号 8

幻灯片编号 9

Quantum dot solar cells

幻灯片编号 11

幻灯片编号 12

k·p method

Next works

Topology optimization and the basic of quantum mechanics Applications Quantum well solar cells Quantum dot solar cells Future works

Time-independent Schrodinger equation: − d 2 2 ψ m dx 2 2 + V ψ ψ E = Which is a wave equation and similar with that of the Electric-magnetic equation. So we will try to extend the method of optimizing EM field to the quantum field.

For a periodic potential, V x a + ( ) = V x ( ) The wave function satisfies ψ ( ψ x a + ) = e iKa ψ x ( ) The solutions of the energy is then a band gap structure nE

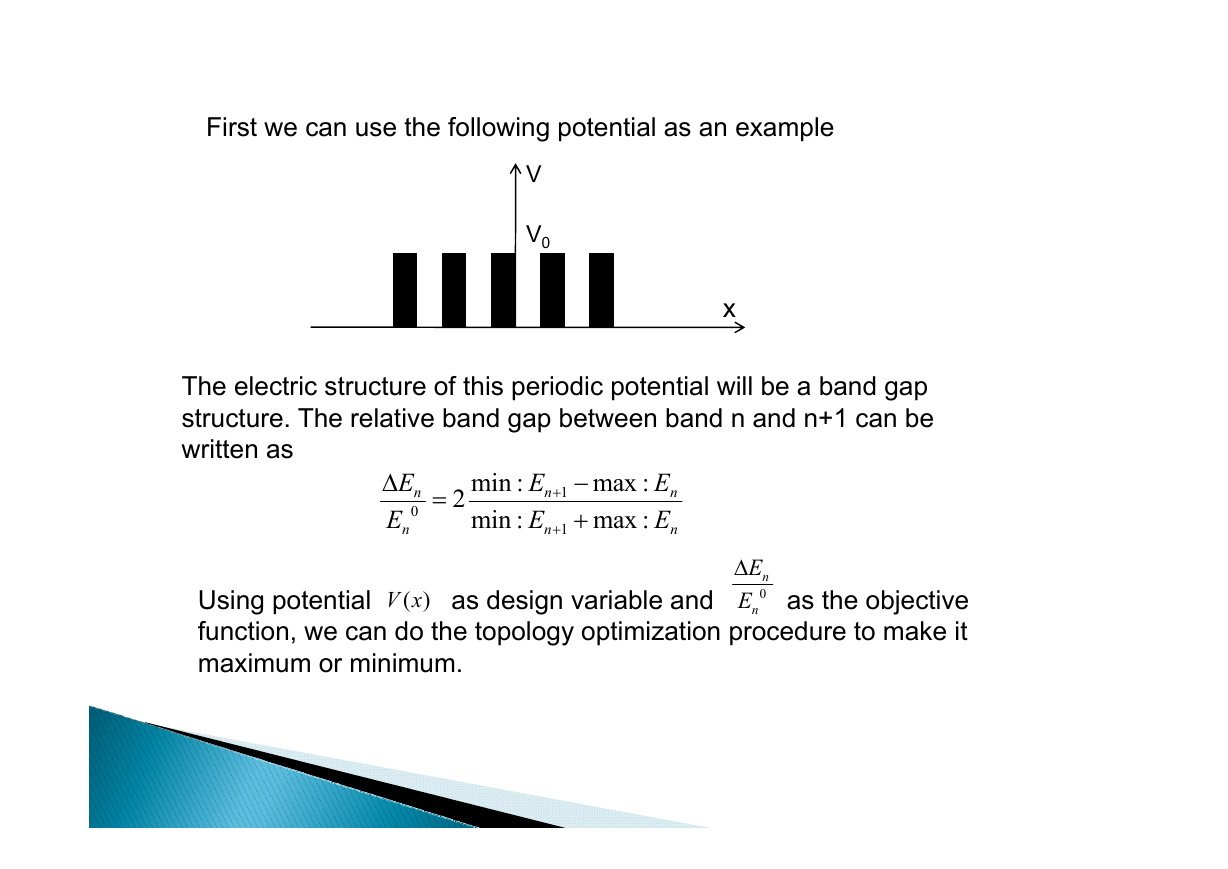
First we can use the following potential as an example V V0 x The electric structure of this periodic potential will be a band gap structure. The relative band gap between band n and n+1 can be written as E Δ n E 0 n = 2 min : min : E n E n − + 1 + 1 + max : max : E n E n ( )V x Using potential as design variable and as the objective function, we can do the topology optimization procedure to make it maximum or minimum. E Δ n E 0 n

In QWSC, the lattice mismatch between the two materials leads to misfit strain in the well, which is reported to have a negative effect on the transition efficiency. Ekins – Daukes (2001) et al. developed the stress-balance method to reduce this effect.

The thicknesses of materials 1 and 2 are selected appropriate such that the lattice constants satisfy According to the experiments of Ekins-Daukes, the efficiency is remarkably improved by strain-balance, and the dark-current is much weaker than the former method. So strain-balanced quantum well is mostly adopted in current studies about QWSC.

But there are still other problems. For example, given two kinds of materials, the thickness of each layer in the quantum well is fixed if we make the strain balanced. While in fact the thickness is also an important factor (Bercowicz et al., 2000; Chen et al., 2008), when the strain is balanced, the efficiency may be not the highest.

分享到：

赞收藏

资料库

经典matlab拓扑优化程序.pdf

相关推荐

开发技术

热门标签

最新资料