logo资料库

商务智能课后作业答案.docx

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：0.23M 资料格式：docx 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    武汉大学计算机学院 2018-2019 第一学期 商务智能-课后作业 1 姓名： 学号： 班级： 陈武桥 2016302580135 软工三班 指导老师： 朱卫平老师 2018 年 10 月 21 日星期日
    1. 请思考数据挖掘可能会遇到哪些法律问题，可能会和哪些法律有 关，请举出具体例子并讨论 1. 隐私安全问题 数据挖掘的首要法律问题在于隐私安全，包括个人隐私，企业信息和国家安全 三个方面。使用数据挖掘技术获取他人的喜好，预测可能的行为是实现商业价值 的一大方式，而这个过程很可能会触犯隐私安全法。首先是数据的来源，数据的 挖掘者是否有权利使用这些数据，数据的获取是否得到了用户的允许，数据的用 途用户是否知情，这些问题都不容忽视，前段时间 Facebook 因为违规获取用户 数据并提供给第三方公司剑桥分析就是一个很好的例子，Facebook 因此而面临 巨额罚款和铺天盖地的骂声。 其次，由数据挖掘而来的数据是否会侵犯用户的隐私，比如我根据他的商品购 买记录推断出他可能有某方面的疾病，并给他推送该类疾病的药物广告。这类问 题当前属于法律的灰色地带，无法明确界定是否违法，但在法律不断完善的今天， 如何确定挖掘的边界也会是数据挖掘工作者必须要考虑的一个问题。 2. 追责问题 假如数据挖掘导致了法律问题，审判机构将如何界定各参与者的责任，很难 有一个确定的标准，因为数据挖掘的不确定性极大，也很难判断问题出在哪一个 环节。举个例子：假如一家数据挖掘公司根据另一数据提供公司的数据挖掘出的 结果导致了不好的后果，问题可能是挖掘算法的问题，也有可能是数据本身就有 问题，预处理人员认为是挖掘算法除了问题，挖掘算法工程师认为是结果转换出 了问题，责任判定十分困难。这还只是最简单的情况，在合作化盛行的今天，一 项业务的开展往往涉及到多个甚至数十个利益相关方，责任的界定在数据挖掘工 作中十分模糊。 2. Skewness 是什么，请计算对称正态分布，正偏移和负偏 移时候的 Skewness 的值（请自行拟定数据分布具体数值） Skewness 指偏度，是统计数据分布偏斜方向和程度的度量，是统计数据分布 非对称程度的数字特征。偏度有正负之分，正偏又称右偏，此时位于均值左边的
    数据多于右边的，即长尾巴拖在右边，负偏则与之相反。正偏时一般算术平均数> 中位数>众数，负偏时相反，即众数>中位数>平均数。正态分布三者相等。 计算公式如下： 下面使用 Excel 进行数据生成和计算，具体内容详见附件。每个类型都进行 了三次以上计算，此处仅举例说明。 正态分布：由于正态分布呈对称性，因此根据定义，Skewness 等于 0。但实际过 程中，数据无法呈现绝对的正态分布，计算结果会有一定误差。 拟定数据：采用随机数生成器，使用标准正态分布（均值= 0， 标准差 = 1）作 为取值概率密度函数，生成 10000 条随机数据 部分数据如图： 使用函数 SKEW 计算得偏度 = -0.023269242。 其余两次计算结果也都接近 0 正偏移
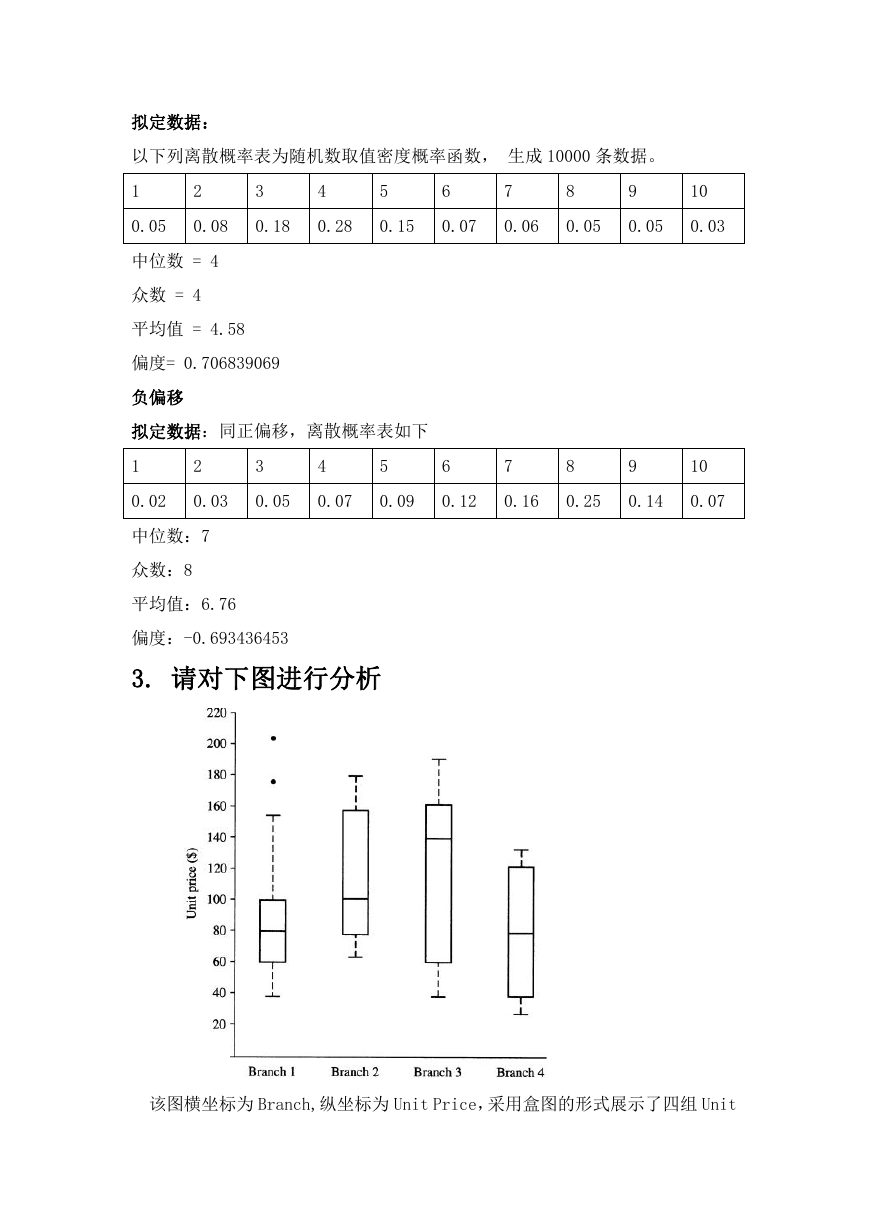
    拟定数据： 以下列离散概率表为随机数取值密度概率函数， 生成 10000 条数据。 1 2 3 4 5 6 7 8 9 10 0.05 0.08 0.18 0.28 0.15 0.07 0.06 0.05 0.05 0.03 中位数 = 4 众数 = 4 平均值 = 4.58 偏度= 0.706839069 负偏移 拟定数据：同正偏移，离散概率表如下 1 2 3 4 5 6 7 8 9 10 0.02 0.03 0.05 0.07 0.09 0.12 0.16 0.25 0.14 0.07 中位数：7 众数：8 平均值：6.76 偏度：-0.693436453 3. 请对下图进行分析 该图横坐标为 Branch,纵坐标为 Unit Price，采用盒图的形式展示了四组 Unit
    Price 数据的分布情况。 鉴于缺乏数据的具体使用环境和评判标准，以下分析均基于数据的分布情况。 最大最小值分布：Branch3 具有最大的最大值，其次是 Branch2, Branch1,Branch4。 Branch4 具有最小的最小值，其次是 Branch1 和 branch3，branch2。 中位数分布：Branch3 的中位数最大，其它依次是 branch2,branch1 和 branch4。 离群点：仅 Branch1 具有两个离群点，数据大于最大观测值。 偏移和离散程度：(不考虑离群点) Branch1: 数据呈现正偏移，中位数附近的数据（上下四分位点之间）较为集 中，上四分位到最大值之间的数据较为离散。 Branch2：数据呈现正偏移，中位数到上四分位数之间的数据较为离散，至最 小值之间的数据较为集中。 Branch3: 数据呈现负偏移，中位数至最大值之间的数据分布比较集中，中位 数到下四分位数据离散程度较高。同时，极差较大，整体离散程度也比较高。 Branch4: 数据分布偏移度很小，对称度很高，两端数据较为集中，整体离散 程度较小。 具体情景举例分析：假设该图描述的是四支股票 30 天内的股价，以最大最小值 的平均值为买入点，则根据图分析，购买呈现负偏移的 Branch3 实现盈利的概率 和盈利的幅值都较大，整体上是一支值得购买的股票。 4. Q-Q plot 中如果两个数据集的数目不相同该如何处理？ 处理的原则是处理后数据数目相同，且数据分布尽可能接近原有数据集。 我将处理方法分为三类，删去、添加和映射。设有数据集 A,B，A 中数据多余 B。在处理过程中，分段能有效优化处理结果。 删去：删去 A 中部分数据，使其与 B 中数据相等。 方法有： 1. 随机删除，更好的方法是分段随机删除，比如 A 中有 100 个数据，要删去 10 个，因此分为 10 段，每段随机删去一个。 2. 定点删除，比如删去尾数为 1 的数据。
    3. 删除首尾，优先从 A 的首部和尾部删去值。 添加：即插值，往 B 中插入部分值，使其与 A 中数据个数相等。 插值位置有：随机插值以及分段随机插值，方法同删去的方法。 插值的值设置方法有：取临近值，取左右两点平均值等。 映射：对于 B 中的点，根据其在 B 中比例位置找到 A 中比例位置最接近的点， 形成映射。反之亦可，原理等同于分段。比如 B 中有 90 个点，A 中 100 个点， B 中第 n 个点对应 A 中与（n/90）*100 最接近的点，如 B8 对应 A9。 5.请自拟数据集计算混合类型相似度矩阵，数据应报告所有 不同的类型，且属性总数目不低于 10 个 第一步：自拟数据集 共设置了 11 种属性，其中标称属性 3 种（包含二元属性），序数属性 4 种， 数值属性 4 种。为了更好地体现混合类型相似度矩阵的计算过程，删掉了部分数 据以达到不对称的效果。 第二步：数据预处理 分类：根据各个属性的类型进行分类 处理：二元属性改为 0 和 1，序数属性根据状态数映射到[0,1]区间：
    第三步：计算 由于数据量计算较为繁琐，我选择采用编写程序的方式进行计算。计算原理是首 先计算相异度矩阵，再根据相似度与相异度和为 1，将相异度矩阵转换成相似度 矩阵。计算相异度矩阵时首先分别计算各类型属性的相异度矩阵，再计算整体相 异度矩阵。 此程序采用欧式距离作为数值和序数属性的相异性衡量标准，重点需要注意 将相异度矩阵的各个值映射到[0,1]区间。 具体代码已在附件中列出，代码语言为 python。 结果如下（仅输出下三角部分） 6.请编写程序实现 Apriori 算法和 FP-Growth 算法，算法可以根据给 定的支持度和置信度获取所有的频繁项集和关联规则。请自拟数据集 进行测试（数据集应按某种方式产生，请描述产生机制，数据集不少 于 1 万条，商品数目不小于 100 种）并汇报以下结果并撰写报告汇报 结果， 1）给定置信度为 80%，关联规则数目随支持度变化的曲线图 2）给定支持度为 30%，关联规则数目随置信度变化的曲线图 3）给定置信度为 80%，请确定某个支持度 s 使得获取的关联规则数目正好大 于 20，请输出 s 和所获取的关联规则数目 7. 请完成 AI Studio 中房价预测例子，并采集一定数目的真
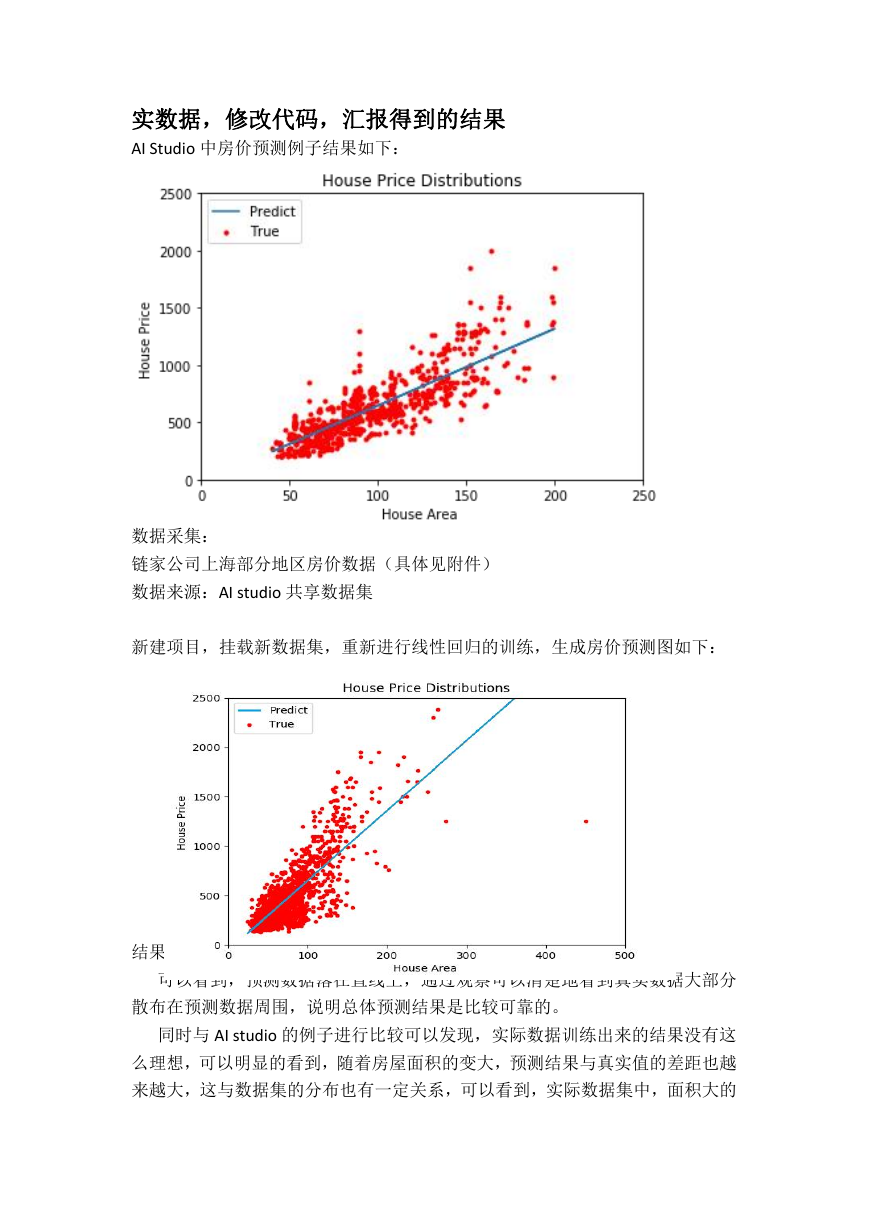
    实数据，修改代码，汇报得到的结果 AI Studio 中房价预测例子结果如下： 数据采集： 链家公司上海部分地区房价数据（具体见附件） 数据来源：AI studio 共享数据集 新建项目，挂载新数据集，重新进行线性回归的训练，生成房价预测图如下： 结果分析： 可以看到，预测数据落在直线上，通过观察可以清楚地看到真实数据大部分 散布在预测数据周围，说明总体预测结果是比较可靠的。 同时与 AI studio 的例子进行比较可以发现，实际数据训练出来的结果没有这 么理想，可以明显的看到，随着房屋面积的变大，预测结果与真实值的差距也越 来越大，这与数据集的分布也有一定关系，可以看到，实际数据集中，面积大的
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料