第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
pandat8.0学习文件.pdf
N. Dupin and I. Ansara: On the Sublattice Formalism Applied to the B2 Phase
N. Dupin and I. Ansara
LTPCM-ENSEEG, S1. Martin d'Heres, France
On the Sublattice Formalism Applied
to the B2 Phase
The B2 phase disorders into the A2 phase. The thermody
namic behaviour of these two phases can be modelled by a
two sublattice (SL) model. A new formulation of this mod
el, designated as modified sublattice (MSL) formalism, has
been introduced to simplify its use to model order-disorder
transformations. The equations allowing the conversion of
the SL model into the MSL formalism are presented in the
binary, ternary and quaternary cases. They show that some
ordering parameters of the MSL are free and should not be
used in an assessment procedure. Two practical cases of
conversion, for the Al- Ni and Ni - Ti systems, are dis
cussed.
1 Introduction
The B2 (CsCl-type) phase disorders into the A2 (W-type)
phase. Figure 1 presents schematically both structures.
For the A2 structure, all the sites of the bee structure are
equivalent whereas for the B2, the site located at the center
of the cell has a different occupation than those at the corner.
The ideal case where a site is fully occupied by A and the
other by B correspond to a compound of stoichiometry AB.
Disordering reactions have been experimentally observed
as first or second order.
To describe the thermodynamic behaviour and phase
equilibria in systems where B2 and A2 were involved, mod
els dedicated to order-disorder transformations, Bragg
William-Gorsky [75Ind, 77Ind, 87Miy], Cluster Variation
Method [9Und, 93Col] or Monte Carlo [88Ack, 91Bic] cal
culations were thus used.
However, experimental evidences had shown that the
non-stoichiometry of some B2 phases were due to triple
defects i.e. anti-structural defects on one side and vacan
cies on the other. The Wagner-Schottky (WS) model intro
duced by Wagner and Schottky [30Wag] to describe the
variation of the Gibbs energy of a compound with different
types of defects was thus also used for those B2 compounds
[68Ett, 75Hen, 76Neul, 76Neu2, 80Hen, 82Hen]. Krachler
et al. [89Kra] have used the WS model to take into account
both types of defects.
Ansara et al. [95Ans, 95Dup] have shown that the WS
model was mathematically equivalent to the two sUblattice
(SL) formalism. A symmetrical description allowing both
defects in the B2 phase was also presented in the particular
case of the Al- Ni system [95Dup, 97Ans 1]. ~-
This paper will present the equivalence of the SL for
malism with the modified sublattice (MSL) formalism in
troduced to simplify the treatment of the order-disorder
transformation in multicomponent systems. The presenta
tion of the formalisms will first introduce the notations.
The parameters of the MSL formalism will then be ex
pressed as function of the SL parameters in binary, ternary
and quaternary cases. Two practical examples of conversion
will then be presented and discussed.
2 Presentation of the Formalisms
The SL formalism, also designated as compound energy
formalism (CEF) [81 Sun, 86And], can be used to model
a complex B2 phase such as (A, B, ... M)(A, B, ... M).
A, B, ... M represent the species, elements or vacancies,
existing in each sublattice, in increasing alphabetical or
der. The Gibbs energy of mixing for one mole of a unit
cell, shown in Fig. 1, is expressed as follows:
L1GSL (y' y") = ~GSL,id(y' y") + ~GSL.XS(v' y")
with
L1G~L.id(y:,y(') = RT L(Y: In Y: + y(' In y(')
mo l '
(1)
(2)
M
I'
I'
m
m
1
1
I
i=A
A GSLxs ('
L.l m
Yi 'Yi = ~ ~ YiYj L.l
")
II AG
i:j + YjYi L.l
II AG )
j:i
'
M-l M
' " '" ( ,
i=A j=i+1
+
M-I M
M
L
i=A j=i+ I k=A
L
L
2
,
'
I J
Y'Y'Yk
II L('
y. - y.
1
')VL(V)
. "k
J i , l -
1'=0
2
M-l M
M
+ '" '" '" II
~ ~ ~YI YJ Yk ~ Y I
i=A j=i+ I k=A
1'=0
II ' ' ' ' ( II _
")VL(v).
k:IJ
YJ
M-l M M-I M
+ ~ ~ ~ ~ YiYjYkY/
' " ' " ' " ' " " " ilL
i=A j=i+ I k=A /=k+ I
ij:k.l
M-2 M-l
+ L
L
M
L
M
L(y:y;y~yf'Lij.k:I+
i=A j=i+ 1 k=i+2 /=A
II
Yi Yj Yk Y/
II
II
'L
)
/:ij,k
(3)
the
The constitution of the phase is described by the site fraction
of
constituents on each sublattice, Y:
and Y('.
~G~Ljd(y:,yn and ~G~L,xs(y:,yn represent
the ideal
Gibbs energy of mixing and the excess Gibbs energy of
mixing respectively. The SL parameters are the Gibbs en
ergies of formation of the stoichiometric compounds, ~Gi:j,
d
an t e mteractIOn parameters,
ij.k:/ an
L/:ij.k. The subscript of each parameter indicates the nature
of the interacting species. Species in the same sublattice are
d h · ·
L(v)
ij:k' Lk:ij ,
(v) L
ij:k.l,
L
76
© Carl Hanser Verlag, Mtinchen Z. Metallkd. 90 (1999) 1
N. Dupin and I. Ansara: On the Sublattice Formalism Applied to the B2 Phase
(a)
(6)
~G~SL(y:,y(') = ~G~SL.id(y:,y(') +- ~G~s.xS(Xi)
+- ~G~d.xs(y:,y(')
(6)
•
o
Figs Ia and b. Schematic crystallographic structure of the A2 and B2
phases. (a) A2, disordered bcc structure: all the sites are equivalent. (b)
B2, ordered bcc structure: the occupation of the site at the center of the
cube is different from the one on the corner.
separated by a comma and those in different ones by a co
lon. The integer v in the parameters L;.I:)k' represents the
order of the interaction. When v = 0, th6 parameter is de
signated as regular; if v = 1 as sub-regular, etc.
Due to the crystallographical symmetry in the case of the
B2 phase, the following relations are introduced:
(v)
(v)
A
A
D.Gj:i = D.Gi:j, Lk:ij = Lij:k, L/:ij.k = Lij,k:I, and LU:ij = Lij:U
(4)
These relations implies that (dG)"II=" = °whatever the site
fractions y! are. They ensure the stability of the disordered
phase [88Ans]. The thermodynamic properties of both or
dered and disordered phases can thus be modelled with a
single expression.
To simplify the optimisation procedure, the Eq. (1) was
expressed as a sum of two contributions, an order dependent
contribution satisfying relations (4) and an order indepen
dent contribution coming from the conversion of the Red
lich-Kister (RK) equation into the SL formalism [88Ans].
This is obtained by expressing the molar compositions Xi
used in the RK equation as function of the site fractions:
1,
Xi = 2Yi +-2Yi
/I
I
(
)
5
The derivation of the expression of the order independent
contribution was introduced by Ansara et al. [88Ans], in
the particular case of the L b phase. A more general case
was treated by Saunders et al. [89Sau]. The first application
of this approach in the case of the B2 phase was presented
by Lacase and Sundman [9ILac].
The conversion of the RK equation into the SL formalism
also allows the derivation a SL description in a binary sys
tem where the B2 is not stable and yet can be used in higher
order systems where the A2/B2 ordering has to be modelled.
However,
the equivalence between the Redlich-Kister
Muggianu (RKM) and the SL formalisms also requires
the introduction of others SL interaction parameters as func
tions of the binary RK parameters [97Ans2]. This conver
sion becomes rapidly tedious and cumbersome when the
number of constituent increases.
relations,
To simplify the thermodynamic description of order
i1J.troduced
disorder
a new formalism was
[9lSun]. Combining SL and RK formalisms,
it is desig
nated as the modified SL (MSL) formalism. It uses a dif
ferent formalism but is mathematically equi~l~t to the
SL model. It expresses the molar Gibbs energy of mixing
of the phases as follows:
~G~SL.id (y!, y:') is the ideal Gibbs energy of mixing of the
phase. It expresses the random mixing of all species in each
sublattice. Related to a mole of site, which is half of the cell
represented in Fig. I, it is equal to half of ~G~L.id(y!,y:').
~G~SL.id(y: ,y(') = RTL 2Y: lny: +- 2Y;' In y;'
M (1
1
)
(7)
I=A
~G~s,xs (Xi) represents the excess Gibbs energy of mixing of
the disordered state of composition Xi. It is expressed by
RKM equation. The thermodynamic parameters of this ex
pression will be designated "disorder" parameters.
~G~S'xs (Xi) = L
M-J M
L
i=A j=i+ I
3
XiXj L (Xi - Xj) VLrj
1'=0
M-2 M-l
+- L
L
M
L
i=A j=i+ I k=i+2
XiXjXkLij,k
(8)
with
(0)
Li\j,k = (Xi +-:3 (I - Xi - Xj - Xk) )Lij,k
1
I
+-(Xj +-:3 (1 - Xi - Xj - Xk) )Lij.k
(I)
(2)
+-(Xk+--(1-xi-Xj-Xk))L.·k
Ij,
1
3
(9)
~G~d.xs(y!, y:') is the ordering Gibbs energy of the phase
whose constitution is given by y: and y('. It is the difference
of the same function, calculated with two different sets of
variables.
(10)
The variables used to evaluate ~G~(y:,y!,) are y! and y!'
while those for ~G~ (Xi, Xi) are Xi and Xi. The thermody
namic parameters of the function ~G~ will be designated
"ordering" parameters. The expression of ~G~(y:, yn is
similar to Eq. (3).
~G~(y:,y(') = L
M-I M
L
i=A j=i+l
(y:y/~G~j +- y;y;'~G;i)
+-
+-
M-J M
M
L
L
i=A j=i+ I k=A
L
M-l M
M
L
L
i=A j=i+ J k=A
L
2
2
1'=0
1'=0
'
,
YY'Yk
)
I
/I L ( '
(v)e
y. - Y
L. "k
I } Ij.
')1'
'
I
YY'Yk
)
,
/I L ( '
(v)e
y. - y. Lk···
I } .Ij
')1'
+- L.- L.- L.- L.- YiYjYk Y/
M-l M M-J M
"""' """' """' """'
i=A j=i+ J k=A /=k+ J
,,1/ /IL e
ij:k,l
M
L(y:y:y£y:'L~,j.k:/
M-2M-J M
L
L
+- L
i=Aj=i+Jk=i+2/=A
)
'Le
/I
+- Yi Yj Yk y/
/I
/I
/:ij.k
(11 )
When the phase is disordered, Y: = y!' = Xi. ~G~(y!,y!,)
thus becomes identical to ~G~(Xi,Xi) and the difference
Z. Metallkd. 90 (1999) 1
77
N. Dupin and I. Ansara: On the Sublattice Formalism Applied to the B2 Phase
of these two terms is equal to zero. ~G~s.xs(Xi) is thus per
fectly defined.
. But due to this difference in Eq. (10), there is an internal
degree of freedom when determining the ordering param
eters. One way to select them is to make ~G~(Xi, Xi) iden
tical to ~G~s,xs(Xi), then ~G~(y:, Y(') represents the excess
Gibbs energy of the ordered phase. Another way could be to
make ~G~(Xi,Xi) equal to zero,
then ~G~(y:,y(') is the
ordering Gibbs energy. Intermediate values are also al
lowed
difference
~G~(y:,y(') - ~G~(Xi,Xi) is meaningful.
~G~(Xi, xJ
Only
the
for
(1).
L A :A .B = L A .B:A = 2LA .B:A + U2.AB + U3.AB
(I).
1 (1)
4
(1).
L BAB = L A .B:B - 2LA .B:B + U2.AB
(I).
_ 1 (I)
_ 4
U3.AB
(2).
L AAB = L A .B:A - 2L A .B:A + U3.AB
(2).
_ 1 (2)
(2).
L A .B:B = L BAB - 2LA,B:B + U3,AB
(2).
_ 1 (2)
3 Identification of Both Formalisms
L~.B:A.B = ~L~.k:A.B - 24 U3.AB
(20)
(21 )
(22)
(23)
(24)
Normally, the MSL Gibbs energy of mixing is referred to
one mole of site while the SL is referred to two moles of
sites. The equivalence of both formalisms can thus be
shown solving the equation
2~GMSL(' ") = ~GSL(y' y")
m
I'
1
m
YI'YI
(12)
whatever the site occupation is. The solution of this Eq. (12)
has been presented in particular cases [88Ans, 89Sau,
97Ans2] expressing the resulting sublattice model param
eters as function of RK and ordering parameters. The
goal was thus to use the SL formalism. The present work
expresses the disorder and ordering parameters of the
MSL formalism as function of the SL parameters, allowing
the conversion of assessments performed with the SL for
malism into the MSL formalism. The relations solving
Eq. (12) will now be presented in binary, ternary and qua
ternary cases.
3.1 Binary Case
For a binary phase modelled as (A, B) (A, B) with the SL
formalism, an equivalent description is obtained with the
MSL formalism provided that the following relations are
fulfilled.
The use of relations (13) to (24) will now be discussed for
different cases of binary systems.
Let us first consider a system where only the ordered B2
phase is stable and its description has been assessed with the
SL model (A, B)(A, B) assuming the symmetry expressed
by relations (4). The conversion above can thus be applied.
The relations (13) to (16) give the expressions of the
disorder parameters. It should be noted that
the use of
sub-sub-regular SL parameters implies sub-sub-sub-regu
parameters,
lar
if
L (2)
Similar remarks can be made for lower or
d~rBi~teracti6~B~arameters. In particular, if only Gibbs en
ergies of formation of the compounds, ,1GA:B, and regular
terms LA(O)B A and L~k B' are used, a sub-regular disorder
term IS generated by Eq. (14), except If LA,B:A = LA,B:B'
disorder
= L (2)
relation
except
(16),
(0)
(0)
.:
:
:
.
.
The relations (17) to (24) give the expressions of the
ordering parameters. The symmetry of the ordering param
eters (~G~:A = ~G~:B and LrtB = L~,!;) is not an assump
tion derived from the crystallographic structure but a result
of the conversion. Whatever is the chosen value for the three
parameters ULAB, U2.AB, U3,AB, the total Gibbs energy calcu
lated is identical.
If UI.AB, U2,AB, U3,AB are taken equal to zero, then all the
ordering parameters are equal to half the corresponding SL
parameters.
~G~:A = ~G~:B = 2~GA:B
1
(25)
(26)
L~,B:A.B = ~ L A .B:A .B
This particular case makes ~G~ (y:, y!') identical to the mo
lar excess Gibbs energy of formation of
the phase.
~G· (x· x·) will thus be the excess Gibbs energy of the dis-
ordered phase, ,1G~s.xs(xJ
(27)
m I'
1
.
But adequately choosing the value of the parameters
Ul,AB, U2,AB, U3,AB can also allow a decrease in the number
of thermodynamic parameters in Eq. (11). For instance, the
following assumptions:
(13)
(14)
(15)
(16)
~
(17)
(0)
(0))
LA,B = ~GA:B + gLA,B:A,B + 2 L A •B:A + LA,B:B
(0)
1
(I)
(I))
LA,B = 2(LA,B:A - LA,B:B + 2 LA,B:A + L A .B:B
(0))
(0)
(1)
1
1 (
1 (
(2)
L A .B = - gLA,B:A,B + 2(LA,B:A - LA,B:B + 2 LA,B:A
(I))
(I)
1
1
~((2)
(2)
+ LA,B:B
)
L(3) = ~ (L(2)
A,B
2
A,B:A
_ L(2)
A,B:B
)
L A :A .B = L A .B:A - 2LA ,B:A + UI,AB + U2.AB + ~,A..!?
(0).
(0).
_ 1 (0)
3
3
(18)
UI.AB = - 2LA,B:A - 3U2,AB -
1 (0)
3U3.AB
(0).
_
LB:A,B -
_ ~L(O)
(0).
L A .B:B - 2 A,B:B + UI,AB
_ 3
U2,AB
+ 3u
3,AB (19)
U2 AB = - - LA B'A - 4U3,AB
1 (1)
2 ' .
.
(28)
(29)
78
Z. Metallkd. 90 (1999) 1
N. Dupin and 1. Ansara: On the Sublattice Formalism Applied to the B2 Phase
1
U3.AB = 42 L AB :A .B
inserted in Eqs (17) to (24) yield
•
~GA:B = ~GB:A = 2:~GA:B - 2:LA.B:A + 2: LA.B:A
1 (0)
3 (I)
•
1
3
+14 L A .B:A .B
L(O). = L(O). = 0
A:A.B
A.B:A
L(O).
BAB
= L(O).
A B B -
_ 1 (0)
2: L A .B:B - 2: L AB :A + L A .B:A
1 (0)
3 (I)
4
+7LA.B:A.B
L(I). = L(I). = 0
A:AB
A,B:A
L(I). = L(I). = ~L(I)
BAB
A.B:B
2 A,B:B
- ~L(l)
2 A.B:A
- ~LAB'A B
21
'"
(2).
L A:A .B = L A .B:A = + 2: L A .B:A + 42 LA.B:A,B
(2).
1 (2)
1
L (2).
_
A.B:B -
(2).
L B A B = + 2: L A .B:B + 42 L A.BAB
1 (2)
1
L~.BAB = 0
(30)
(31 )
(32)
(33)
(34)
(35)
(36)
(37)
(38)
For a system A - B where only the disordered phase A2 is
stable, it has been proposed to introduce the contribution of
the A - B interaction to the B2 description identifying the
SL formalism and the RK equation. The SL parameters ob
tained, previously derived by Saunders [89Sau] are given
in the Appendix. Assuming
UI.AB = - 4" LA,B
1 (O)RK
U2.AB = - 8' LA,B
(I )RK
I
U3.AB = -1"6 L A .B
(2)RK
1
(39)
relations (13) to (24) with the SL parameters (93) to (100)
simply yield:
L(O) = L(O)RK L(I) = L(I)RK and L(2) = L(2)RK
A,B
A.B' A,B
(40)
A,B
A,B
A.B
All the ordering parameters (17) to (24) are equal to zero.
This is the main advantage of the introduction of the MSL
formalism. It becomes crucial when the number of consti
tuents increases.
If the description of a metastable ordered phase is needed
in such a system, the assessment of the ordering parameters
can be performed using either results from first principles
calculations or those derived from experiments in higher
order systems. This procedure will not affect the stable dis
ordered state. When adding ordering parameters, special
care must be taken to avoid making the ordered phase
stable.
The last case to consider is the one where both ordered
and disordered phases are stable in the binary system A -- B.
If the order-disorder transition is stable and tJ).e.assessment
uses the SL formalism to describe it, relations (13) to (24)
then allow an easy conversion. If the order-disorder transi
tion has not been modelled, the assessment of the ordering
Z. Metallkd. 90 (1999) 1
parameters of the MSL formalism is possible without
changing the equilibria involving the ordered phase. But
it should be emphasized that a limited number of indepen
dent thermodvnamic parameters are available. For instance,
(16)
l' k d
(2).
L AB :A and L A .B:A are III e
,
(22) and (23). The inversion of the Eqs. (13) to (24) can then
produce the SL parameters if they are needed. They are
presented in the Appendix by Eqs (102) to (109).
to L A .B as sown y
b E
qs
('2).
(3)
h
When the order-disorder transition is metastable, both
phases are sometimes modelled as separate phases: the or
dered one with the SL formalism and the disordered one
with the RK equation. Merging the two descriptions into
a single one using MSL will then be possible only if rela
tions (13) to (16) produce disorder parameters identical to
the RK parameters assessed independently. This is gener
ally not
the case, unless it has been done on purpose.
This case will be illustrated in the example section for
the Ni - Ti system.
3.2 Ternary Case
The ternary case corresponds to a ternary phase or to a bi
nary phase for which vacancies exist on both sublattices.
With relations (13) to (24) fulfilled in each binary sub-sys
tem, the identification of both formalisms yields the follow
ing, independent of the value UABC:
L(2)
AB:C
=L(2)
CAB
=~L(2)
2 A.B:A
+~L(2)
2 A.B:B
L(2)
AC:B
= L(2)
BAC
L(2)
B.C:A
= L(2)
AB.C
= ~L(2) + ~L(2)
2 AC:A
2 A,C:C
= ~L(2) + ~L(2)
2 B.C:B
2 B,C:C
(41)
(42)
(43)
(0)
L A .B.C = LAB.C:A -
1
4" LA,B:A,B + LA.BAC -
1
4" LA,CAC
1
- gLB,C:B,C -
(0)
1
"2 (LA,B:A + LA,B:B) + LA,B:C
(0)
(0)
- 2: (LA,C:A + LA,c:d + LA,C:B + LB,c:A
(0)
(0)
(0)
- 2: (LB,C:B + LB,c:d - 2: (LA,B:A + L AB :B + LA,B:C
(I))
(I)
(0)
1
(I)
-2:(LA ,C:A +LA,C:c +LA,C:B
(I))
(I)
(0)
(0)
(I)
1
1
1
1
1
1
(I)
_
L A .B.C - +LA.B.C:B -
1
4" LA,B:A.B + LAB:B.C - 8' LAC:A,C
1
- 4"LB,C:B,C -"2 (LA,B:A + LA,B:B + LA,B:C
(0))
(0)
(0)
1
(0)
- 2: (LA,C:A + L A,c:C) + L A,C:B + LB,C:A
(0)
(0)
(0)
(0)
(I))
- 2: (LB.C:B + LB,c:d + 2: (LA,B:A + LA,B:B
(I)
(0)
1
(I)
(I))
-LA .B:C + LB.C:A - 2: (LB,C:B + LB,C:c
(I)
(I)
1
(2)
LA,B,C = LA,B,C:C - 8' LA,B:A,B -
1
1
4" LA,C:A,C + LA,C:B,C
(44)
(45)
79
N. Dupin and I. Ansara: On the Sublattice Formalism Applied to the B2 Phase
1
1
1
- 4: LB .C:B.C -"2 (LA.B:A + LA.B:B) + LA.B:C
(0)
(0)
1
(0)
(0)
-"2 (LA .C:A + LA.c:d + LA.C:B + LB.C:A
(0)
(0)
(0)
(0)
(0)
-"2 (LB,C:B + LB,c:d +"2 (LA.C:A + LA.c:d
(I)
1
(I)
(I)
-LA,C:B - LB.C:A +"2 (LB.C:B + LB,c:d
(I)
(I)
1
(I)
(0).
LA.B:C = L CAB = "2 LA,B:C + Ul,AB - U2.AC - U2.BC
(0).
1
(0).
LA.C:B = LB:A,C = "2LA,C:B + UI,AC - U2.AB + U2,BC
(0).
1
(0).
_
LB.C:A -
(0).
L A :B.C -
_ 1
"2 LB.C:A + UI.BC + U2.AB + U2.AC
(I).
A B:C -
L
- L(I).
C:A B = "2 LA,B:C + U2,AB -
1 (I)
1
"2 U3,AC +"2 U3,BC
1
(50)
(51 )
(52)
(53)
(54)
(55)
1
1
(2).
LA,B:C = L CAB = 4: (L A .B :A + LA,B:B) + U3,AB
(2).
(2)
(2)
(2).
LA,C:B = LB:A,C = 4: (LA,C:A + LA,c:d + U3,AC
(2).
(2)
(2)
(2).
LB.C:A = LA:B,C = 4: (LB,C:B + LB.c:d + U3,BC
(2).
(2)
1
(2)
L•
A,B:A,C = LA,C:A.B = "2 LA,BAC -
1
•
5U3.AB - 5U3.AC -
2U3,BC
•
•
LA.B.C:A = L A :A .B.C = "2 LA.B.C:A + "2 U3.AB + "2 U3.AC - U3.BC
(59)
+ UABC
1
1
1
•
A.B.C:B
L
= L
•
B:A.B.C
+ UABC
(46)
= -LABC'B +-U~AB - U~AC +-U~BC
oJ.
.. ,
1
2 oJ.
1
2 oJ.
1
2
(60)
L.
A.B.C:C -
_ L·
1 L
C A.B C ="2 A.B.C:C - U3.AB + "2 U3.AC + "2 U3.BC
(61 )
1
1
The relations (41) to (43) have to be fulfilled by the SL
ternary sub-sub-regular to solve Eq. (12) in the ternary
case. If, during the assessment of the description to con-
vert,
een
made, the conversion could be impossible unless the value
of such high order terms, L;~;k' have no influence on the
Gibbs energy of the stable configuration.
t e assumptIOn L ij:k = 2. Lij:i + 2. Lij:j
h
as not
(2) h
(2)
(2)
b
.
I
I
The relations (44) to (46) give the ternary disorder inter
action parameters. They do not depend on the binary vari
ables ul.ij, U2.ij, U3.ij or the ternary one UABC. In the general
case, they have different values. But, if
LA.B.C:A = LA.B.C:B = LA.B.C:C = LA.B.C:*
and
(62)
(I)
(I)
(I)
L ij:A = L ij:B = Lij:c
and
(\,)
L ij:k.1 = 0
then they are identical and equal to:
LA,B,C = LA.B.c:* -"2 (L A .B:A + L A .B :B ) + L A .B:C -
(0)
(0)
1
(0)
(63)
(64)
(0)
1
"2 (LA,C:A
(0))
+ LA,C:c + LA.C:B -
(0)
(0)
(0)
1
"2 (LB,C:B + LB.c:d + LB,C:A
(65)
.(0)
The relations (47) to (61) give the ternary ordering
parameters. The values of these parameters depend on
the choice made for the binary free variables Ui.AB, Ui,AC,
Ui.BC, as well as for UABC. The case where all the ordering
parameter are equal to half of the corresponding SL param
eters, as (25) to (27), is still a particular case of conversion.
The expression of the ternary SL parameters obtained by
converting the RKM equation into the SL formalism, given
in the appendix, can be converted using LA,B.C = L~~,c' As
in the binary case, all the ordering terms cancel if the free
parameters are adequately chosen. This result is very inter
esting because it avoids the use of the relations (92) to (l00).
(56)
3.3 Quaternary Case
L•
A,B:B.C = LB.C:A.B .= "2 LA,B:B,C - 5U3,AB -
1
•
2U3.AC -: 5U3.BC
A.C:B.C = LB.C:A.C = "2 LA,C:B,C -
L·
•
1
..,-
2U3,AB - 5U3,AC -
(57)
5U3,BC
(58)
This case corresponds to a quaternary phase or to a ternary
phase allowing substitution of vacancies on both sublat
tices. The conversion from the SLF to the MSL formalism
is obtained as long as the thermodynamic description in all
sub-systems, binary and ternary systems fulfill the general
relations presented in the previous sections and the follow
ing:
80
Z. Metallkd. 90 (1999) 1
N. Dupin and I. Ansara: On the Sublattice Formalism Applied to the B2 Phase
L AB .D:C = LC:A.B.D - 6(L A .B:A .B + LA.C:A.C + L A .D:A .D
1
4 Examples of Conversion
+LB.C:B.C + L B.D:B.D + LC.D:C.D) + "3 (LA.B:A.C
1
+LA .B:A .D + L A .B:B .C + L A .B:B .D + LA.C:A.D
+LA,C:B.C + LAc:C,D + LA,D:B.D + LA.D:C.D
+LB.C:B.D + LB.C:C.D + LB,D:C.D + LA.B.C:A
+LA,B,C:B + LAB,C:C + L A .B .D:A + L A .B.D:B
+LA.B,D:D + LA.C.D:A + LA.C.D:C + LA.C.D:D
+LB,C.D:B + LB.C.D:C + LB,c,D:D) - LA,B:C,D
The relations obtained in the previous section will be used to
convert the thermodynamic description of the B2 phase in
two practical cases: the binary systems Al- Ni and Ni - Ti.
These two phases were initially described with the asymme
trical model (Ni, B) (B, D) where 0 represents vacancies
and B is Al or Ti. Before applying the conversion rela
tions, it is necessary to make the SL description symmetri
cal as (Ni,B, o)(Ni, B, D).
In the Al- Ni system, the A2 phase is not stable and has
not been assessed. In the Ni - Ti system, the A2 phase is
stable and has been assessed as a different phase.
-LA,C:B.D - LA,D:B.C - LA,B,C:D - LA.C,D:B
4.1 AI-Ni
-LB,c,D:A
(66)
•
LA,B,C:D = LD:A,B.C = "2 LAB,C:D - U3,AB - U3.AC + U3,AD
1
•
-U3.BC + U3.BD + U3.CD + UABC
(67)
•
L A .B.D:C = LC:A.B.D = "2 LA.B,D:C - U3,AB + U3.AC - U3.AD
•
I
+U3.BC - U3.BD + U3.CD + UABD
(68)
•
L A .C.D:B = L B:A .C .D = "2 L AC .D:B + U3.AB - U3,AC - U3.AD
•
I
+U3.BC + U3.BD - U3.CD + UACD
(69)
Initially, the B2 phase was modelled (AI, Ni) (Ni, D). The
symmetrical description should be (AI, Ni, D) (AI, Ni, D)
without changing the thermodynamic behaviour of the
phase. During the assessment procedure, the following hy
potheses were used (in kJ/mol):
A A2
L..\GNi:Ni = 2L..\GNi
(74)
B2
A
L\G
B2
AI:D -
- L\G
A2 + 10 - T 10- 3
Al
.
L\GB2
Ni:D =
L\GB2
Ni:Ni + L..\ AI:D - L..\GAI:Ni
A B2
AGB2
L B2 . = L B2 . .
AI.Nl:D
AI.NI:Nl
(75)
(76)
(77)
•
LB,C.D:A = LA:B.C,D = "2 LB.C,D:A + U3,AB + U3.AC + U3.AD
•
I
-U3.BC - U3.BD - U3.CD + UBCD
•
LAB:C,D = LC.D:A.B = "2 LA,B:C,D -
•
I
2U3,AC -
2U3,AD
- 2U3,BC -
2U3,BD
(70)
(71 )
.
L
. = L
B2
AI:NI.D
B2
Nl:Nl.D
Thus only three parameters L\G~T:Ni' L~T.Ni:Ni and L~?:Ni.D
were assessed. The Gibbs energy obtained with this model
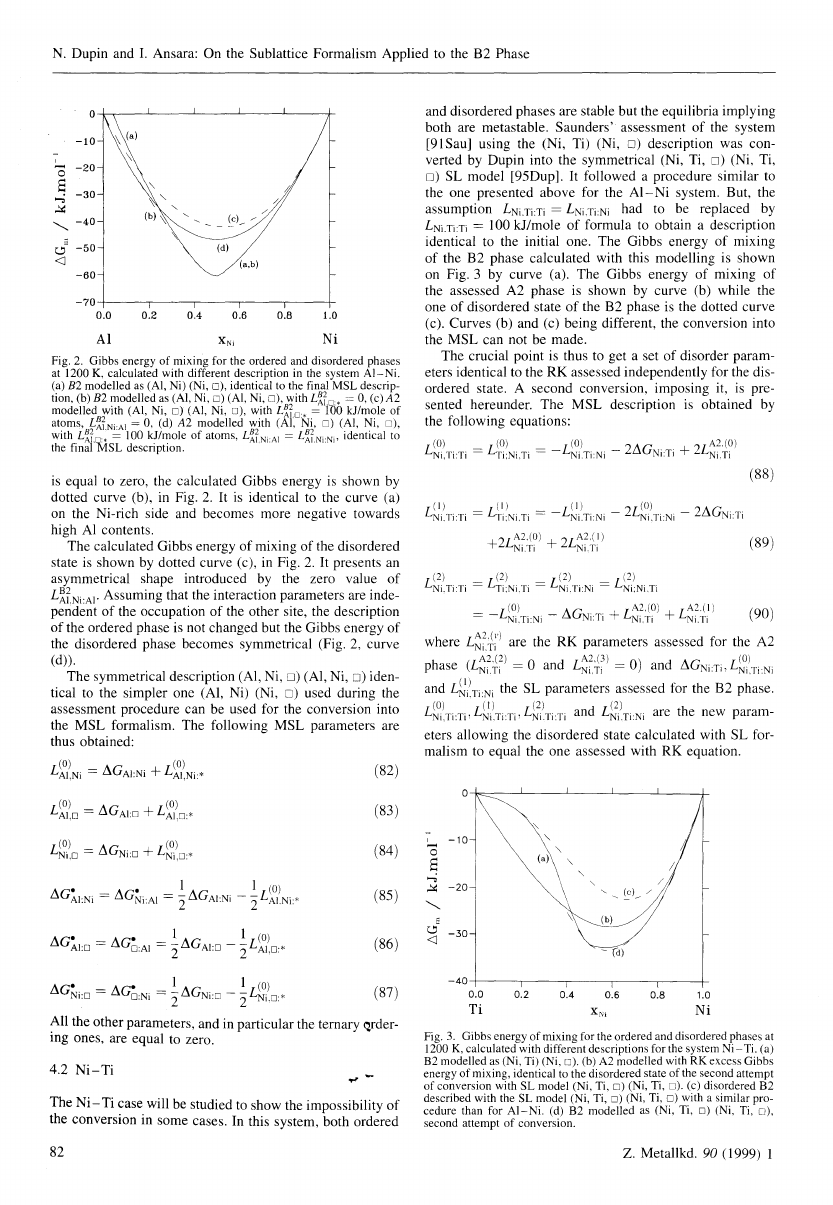
at 1200 K is shown by curve (a) in Fig. 2.
(78)
Changing this description into the symmetrical model
(AI, Ni, D) (AI, Ni, D), always using the SL formalism,
was made by applying relations (4)
to the parameters
(74)
to (78) and introducing the following hypothesis
[97AnsI].
•
LA,c:B,D = LB,D:A,C = "2 LA,C:B,D -
1
•
2U3,AB -
2U3,AD -
2U3,BC
-2U3.CD
(72)
L\G
B2 = 0 1
D:D
(79)
(80)
•
LA,D:B.C = LB.C:A.D = "2 LA,D:B.C -
•
I
2U3,AB -
2U3,AC -
2U3,BD
L B2
Al,D:Al = Al.D:Ni = AI,D:D = LAI:AI,D = Ni:AI,D
LB2
L B2
L B2
B2
-2U3.CD
(73)
To solve Eq. (12) in the quaternary case, the parameter (66)
is not free. It is a function of the parameters of the type Lij:ij,
Lij:i,k and LiJ,k:1 which are generally set to zero in a assess
ment. Moreover, the number of description of ternary or
quaternary system currently available, where this conver
sion could be applied,
is so small that the relations (66)
to (73) could have almost no practical application. Because
the MSL is an improvement in the assessment Procedure as
well as in the database managing, the use of the SL form
alism in the study of phases presenting order-disorder re
lations should be avoided for multicomponw-t..systems.
It can be noted that the only binary parameters in the
expression of the quaternary ordering parameters (67) to
(73) are U3,ij'
= L~~AI.D = 100 kJ jmole of formula unit
(81)
2
default,
Bl
~11 the other parameters, L~?Ni:AI' L~?:Al.Ni'
LNi.D:D, and LD:Ni.D' were then kept equal to zero. The intro
duction of a high positive value for the interaction of Al and
o (Eq. (81) was necessary to avoid the introduction of va
cancies on the Al sublattice, as they were forbidden in the
model (AI, Ni) (Ni, D). The calculated Gibbs energy is then
also represented by curve (a) in Fig. 2. If the parameter (81)
I For numerical reasons, it seems necessary to change this value to
a small positive value, as 10- 1°, to avoid the stabilisation of an
almost totally empty state.
Z. Metallkd. 90 (1999) 1
81
N. Dupin and I. Ansara: On the Sublattice Formalism Applied to the B2 Phase
0
-10
I
"0 -20
S -30
....;
~
""" -40
1.:)- -50
N. Dupin and I. Ansara: On the Sublattice Formalism Applied to the B2 Phase
2000 -t------!....-------'--------'--------'----____t_
~ 1500
vl-.
;j
~
l-.
Q)
0-
S
~ 1000
500 -t----,----!....----,-----l----,-----'-----,------l-j-
1.0
Ni.
0.0
Ti
0.4
0.2
0.6
0.8
X Ni
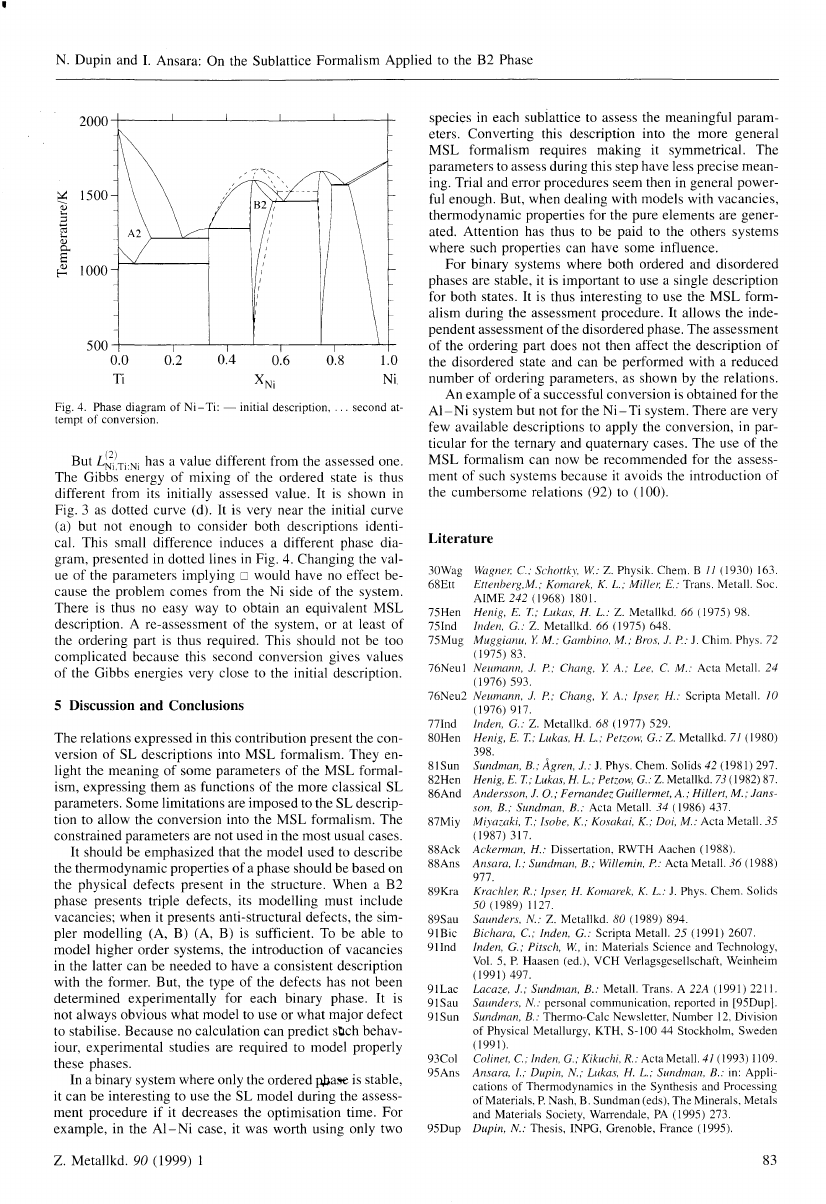
Fig. 4. Phase diagram of Ni- Ti: -
tempt of conversion.
initial description, ' .. second at
But L~i~Ti:Ni has a value different from the assessed one.
The Gibbs energy of mixing of the ordered state is thus
different from its initially assessed value. It is shown in
Fig. 3 as dotted curve (d). It is very near the initial curve
(a) but not enough to consider both descriptions identi
cal. This small difference induces a different phase dia
gram, presented in dotted lines in Fig. 4. Changing the val
ue of the parameters implying D would have no effect be
cause the problem comes from the Ni side of the system.
There is thus no easy way to obtain an equivalent MSL
description. A re-assessment of the system, or at least of
the ordering part is thus required. This should not be too
complicated because this second conversion gives values
of the Gibbs energies very close to the initial description.
5 Discussion and Conclusions
The relations expressed in this contribution present the con
version of SL descriptions into MSL formalism. They en
light the meaning of some parameters of the MSL formal
ism, expressing them as functions of the more classical SL
parameters. Some limitations are imposed to the SL descrip
tion to allow the conversion into the MSL formalism. The
constrained parameters are not used in the most usual cases.
It should be emphasized that the model used to describe
the thermodynamic properties of a phase should be based on
the physical defects present in the structure. When a B2
phase presents triple defects,
its modelling must include
vacancies; when it presents anti-structural defects, the sim
pler modelling (A, B) (A, B) is sufficient. To be able to
model higher order systems, the introduction of vacancies
in the latter can be needed to have a consistent description
with the former. But, the type of the defects has not been
determined experimentally for each binary phase.
is
not always obvious what model to use or what major defect
to stabilise. Because no calculation can predict stlch behav
iour, experimental studies are required to model properly
these phases.
It
In a binary system where only the ordered pJla~ is stable,
it can be interesting to use the SL model during the assess
ment procedure if it decreases the optimisation time. For
example, in the AI- Ni case, it was worth using only two
Z. Metallkd. 90 (1999) 1
species in each subiattice to assess the meaningful param
eters. Converting this description into the more general
MSL formalism requires making it symmetrical. The
parameters to assess during this step have less precise mean
ing. Trial and error procedures seem then in general power
ful enough. But, when dealing with models with vacancies,
thermodynamic properties for the pure elements are gener
ated. Attention has thus to be paid to the others systems
where such properties can have some influence.
For binary systems where both ordered and disordered
phases are stable, it is important to use a single description
for both states. It is thus interesting to use the MSL form
alism during the assessment procedure. It allows the inde
pendent assessment ofthe disordered phase. The assessment
of the ordering part does not then affect the description of
the disordered state and can be performed with a reduced
number of ordering parameters, as shown by the relations.
An example of a successful conversion is obtained for the
AI- Ni system but not for the Ni - Ti system. There are very
few available descriptions to apply the conversion, in par
ticular for the ternary and quaternary cases. The use of the
MSL formalism can now be recommended for the assess
ment of such systems because it avoids the introduction of
the cumbersome relations (92) to (l00).
Literature
30Wag Wagner, C; Schottk}', W: Z. Physik. Chern. B II (1930) 163.
Ettenberg,M.; Komarek, K. L.; Miller, E: Trans. Metal\. Soc.
68Ett
AIME 242 (1968) 1801.
75Hen Henig, E T.; Lukas, H L.: Z. Metallkd. 66 (1975) 98.
75Ind
75Mug Muggianu, Y M.; Gambino, M.; Bros, 1. P: J. Chim. Phys. 72
Inden, G.: Z. Metallkd. 66 (1975) 648.
(1975) 83.
76Neul Neumann, J. P; Chang, Y A.; Lee, C M.: Acta Metal\. 24
(1976) 593.
76Neu2 Neumann, 1. P; Chang, Y A.; Ipser, H: Scripta Metal!. 10
(1976) 917.
Inden, G.: Z. Metallkd. 68 (1977) 529.
77Ind
80Hen Henig, E T.; Lukas, H L.; Petzow, G.: Z. Metallkd. 71 (1980)
398.
Sundman, B.; Agren, J.: 1. Phys. Chern. Solids 42 (1981) 297.
81Sun
82Hen Henig, E T.; Lukas, H L.; PetlOw, G.: Z. Metallkd. 73 (1982) 87.
86And Andersson, J. 0.; Fernandez Guillermet, A.; Hillert, M.; Jans-
son, B.; Sundman, B.: Acta Metal!. 34 (1986) 437.
87Miy Miyazaki, T.; Isobe, K.; Kosakai, K.; Doi, M.: Acta Metal\. 35
(1987) 317.
88Ack Ackerman, H: Dissertation, RWTH Aachen (1988).
88Ans Ansara, I.; Sundman, B.; Willemin, P: Acta Metal\. 36 (1988)
89Kra
89Sau
91Bic
91Ind
91Lac
91Sau
91Sun
977.
Krachler, R.; Ipser, H Komarek, K. L.: 1. Phys. Chern. Solids
50 (1989) 1127.
Saunders, N: Z. Metallkd. 80 (1989) 894.
Bichara, C; Inden, G.: Scripta Metal!. 25 (1991) 2607.
Inden, G.; Pitsch, W, in: Materials Science and Technology,
Vol. 5, P. Haasen (ed.), VCH Verlagsgesellschaft, Weinheim
(1991) 497.
Lacaze, 1.; Sundman, B.: Metall. Trans. A 22A (1991) 2211.
Saunders, N: personal communication, reported in [95Dup].
Sundman, B.: Thermo-Calc Newsletter, Number 12, Division
of Physical Metallurgy, KTH, S-100 44 Stockholm, Sweden
(1991).
Colinet, C; Inden, G.; Kikuchi, R.: Acta Metal\. 4 I (1993) 1109.
93Col
95Ans Ansara, I.; Dupin, N; Lukas, H L.; Sundman, B.: in: Appli
cations of Thermodynamics in the Synthesis and Processing
of Materials, P. Nash, B. Sundman (eds), The Minerals, Metals
and Materials Society, Warrendale, PA (1995) 273.
95Dup Dupin, N: Thesis, INPG, Grenoble, France (1995).
83
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
