第 27 卷 第 2 期 农 业 工 程 学 报 Vol.27 No.2 2011 年 2 月 Transactions of the CSAE Feb. 2011 307 温室温度控制系统的神经网络 PID 控制 屈 毅 1，宁 铎 2 ，赖展翅 1，程 琪 1 ，穆丽宁 1 （1．咸阳职业技术学院电信系，咸阳 712000； 2．陕西科技大学电信学院，西安 710021） 摘 要：建立温室温度控制系统的数学模型。针对温室温度控制系统存在的大滞后、大惯性等问题,考虑到常规 PID 控制 器自适应能力差、鲁棒性不强等缺陷，提出采用将具有较强的自组织、自学习和自适应能力的径向基神经网络与常规 PID 相结合构成 RBF-PID 控制策略，自适应调整 PID 控制器的参数。在该控制策略中，采用 RBF 神经网络辨识器实现温度 控制系统的 Jacobian 矩阵信息在线辨识，对 RBF-PID 控制器控制参数在线自整定。研究结果表明：RBF-PID 控制器可 使温室温度控制系统动态响应快、鲁棒性强、稳态精度高、超调量小、抗扰动能力强，具有良好的控制效果。 关键词：温室，神经网络，自适应，数学模型 温度控制 doi：10.3969/j.issn.1002-6819.2011.02.053 中图分类号：TP183 文献标志码：A 文章编号：1002-6819(2011)-02-0307-05 屈 毅，宁 铎 ，赖展翅，等. 温室温度控制系统的神经网络 PID 控制[J]. 农业工程学报，2011，27(2)：307－311. Qu Yi , Ning Duo, Lai Zhanchi, et al. Neural networks based on PID control for greenhouse temperature[J]. Transactions of the CSAE, 2011, 27(2): 307－311. (in Chinese with English abstract) 藉此可忽略温室内空气与土壤表层间的热量交换；2）在 本文计算土壤传热时，可忽略温室内土壤的横向传热， 只考虑纵向方向的一维传热；3）温室内的农作物(如西红 柿)冠层温度分布均匀。 考虑到农作物蒸腾作用对于温室内温湿度的影响， 采用文献[1]提出的含控制量的温室温度数学模型, 见式 （1）。等式（1）右边各项依次为通过温室覆盖层交换的 热量、通风时温室内外的热量交换、温室吸收的太阳能、 作物蒸腾作用吸收的热量和温度调控设施所提供的热 量。 V c ρ ρ T d in t d = h A T ( c c T t ( )) in − t ( ) T t in out kQ t ( ) ( )) + ρ c V t T ( )( ρ in t ( ) − out t ( c d ) rad + − + heat λ ( ) E t A Q t − （1） 温室内种植的农作物蒸腾作用会影响到温室环境温 度和湿度，是进行温室温度控制所必需考虑的因素。通 过对陕西关中中部地区，夏季和冬季温室小气候和蒸腾 速率的实验数据分析，参照文献[3]提出的方法，计算得 出夏季和冬季陕西关中地区温室农作物蒸腾速率与温室 环境气候要素之间的定量关系式见式（2）～式（4）所 示。 E winter : λ = ⎧ ⎨ E summer : λ ⎩ Q 0.24 rad Q 0.25 = + 75.2 VPD in （2） e in rad T 17.4 in T 239 + in （4） RH ) 温室的温度控制模型如式（1）所示，其中 Qheat(t)的 （3） 0.6107exp VPD in e in (1 = = − in 表达式如式（5）所示。 t ( ) Q （5） 把式（5）代入式（1），并对式（1）进行变换整理， C Heat t ( ) heat = ⋅ h 0 引 言 现代温室能够通过人工控制温室内环境因素，满足 农作物的最佳生长条件，使农作物生长环境得到优化， 有效地改善农业生态，提高土地的产出率和社会经济效 益。大量的理论和实践研究结果表明：合适的生态环境， 尤其是合适的温度环境，能够大幅提高农作物的产量。 但温室环境系统由于自身的复杂性，各种环境因素之间 相互影响，采用传统的控制方法很难达到最佳的控制效 果[1]。 为此，将神经网络与常规 PID 控制律相融合，充分 利用径向基函数神经网络（radical basis function，RBF） 非线性映射能力和学习力，实时调整 PID 控制器的控制 参数，构成的参数可调、自适应性强的神经网络 RBF-PID 控制器。该控制器可以很好的实现温室温度系统的高品 质控制[2]。 1 温室温度控制系统数学模型 因不同地区温、光、水、气、肥等条件的不同，所 建立的温室温度控制系统模型从结构到控制方法有很大 的不同。本文以陕西关中地区温室的物理过程进行分析。 此类温室结构是热水管道加热、单层透明覆盖物（薄膜 或玻璃）、天窗通风以及农作物生长环境的自动控制。 依据该地区温室的实际情况，为了重点突出研究对 象的本质，在建立温室温度控制系统的数学模型时必须 对研究对象作必要的简化：1）温室内农作物生长的空气 环境均匀，温室内空气温度与土壤表层温度可视为相同， 收稿日期：2010-07-22 修订日期：2010-12-12 作者简介：屈 毅（1974－），男，陕西乾县人，博士研究生，主要从事随 机分布控制、鲁棒控制以及非线性系统研究。咸阳 咸阳职业技术学院电信 系，712000。Email: quyi0709052@163.com. 

农业工程学报 2011 年 308 h A c V t ( ) c in 得到式（6）。 ρ T d c ρ in V c t d ρ ρ c V t h A ( )) ⋅ c c ρ = − ρ + ( in ⋅ T t ( ) in + T s ( ) in = λ E t A C H t ( ( ) + eat h − t d ) T out t ( ) + − kQ t ( ) rad V c ρ ρ = L t M t T ( ) ⋅ M t ( ) ( ) = （6） （7） h A c V t ( ) ρρ + c c in （8） E t Aλ t kQ t ( ) ( ) − + ( ) rad out 把式（7）和式（8）代入式（6）得到式（9） d T t ( ) in t d = − M t T t ( ) ( ) V c ρ ρ in ⋅ + L t C H t ( ) ( + h eat V c ρ ρ − t d ) （9） 式中，M(t)为受温室覆盖层与温室内气体定容比、温室体 积、温室覆盖层的面积、温室内自然通风率、热温室内 气体的对流换热系数的影响。L(t)项是由室外温度 Tout(t)、 作物蒸发潜能速率 λE、投在温室覆盖层的太阳辐射 Qrad(t) 等环境变量构成，可以作为干扰项处理。综上可知，温 室温度系统是一个复杂、参数是时变的系统。 参考陕西关中地区一温室连续 30 d 从 8:00 到 17:00 观测数据，对 M(t)变化情况进行分析，发现 M(t)值介于 36 335.023 与 36 654.98 之间，平均值为 3 649，相对平均 值变化率为-0.44%～0.43%。这样 M(t)可当作常数，用其 平均值 M′来代替。则式（9）变为式（10）。 L t C Heat t ( ) ( ′ − + d ) t d （10） T t ( ) in t d = − ⋅ M T t ′ ( ) V c ρ ρ L t M T ( ) ′ ⋅ = in + ⋅ h V c ρ ρ E t A ( ) （11） 对式（10）两边进行拉氏变换，并将式（11）代入， kQ t ( ) λ + − rad out ⋅ ′ 整理得到式（12） T s ( ) in ⋅ = C e Heat s ( ) h M ′ dt s − V c ρ ρ M ′ L s M T ( ) ′ ′ ⋅ S ⋅ + s ( ) 1 + 1 M ⋅ ′ L s ( ) ′ S ⋅ + V c ρ ρ M ′ Es Aλ ) ⋅ out rad − + = kQ （13） 式中，Tin 为温室内环境温度，℃；Tout 为温室外环境温度， ℃；V 为温室内的体积，m3；ρ 为空气密度（1.2 kg/m2）； cρ 为温室内气体定容比热（1.005 J/(kg·℃)）；k 为太阳辐 射能被温室空气吸收的传热系数；hc 为温室覆盖层与温 室内气体的对流换热系数；Ac 为温室覆盖层的面积，m2； λE 为农作物蒸发潜能速率，m/s；Vin 为温室内自然通风 率，m3/s；Qrad 为投在温室覆盖层的太阳辐射，W/m2； Qheat 为加热器的加热功率，W；RHin 为温室内空气相对 湿度；ein 为中间变量；VPDin 为温室内空气饱和水汽压差； Ch 为加热源的传导系数；Heat(t)为温度调控设施控制输 出的函数。 由式（12）可以看出，此温室温度系统可近似为有 扰动情况下的一阶惯性加时滞环节，Heat(S)是温度调控 设施控制输出的传递函数。在典型的一阶惯性加时滞环 节中，K 是系统的静态增益，T 是系统时间常数，τ 是系 统纯滞后时间。我们将温室温度模型与典型的一阶惯性 加时滞环节进行对照，得到式（14）和式（15）。 ⋅ C e Heat s ( ) h M ′ dt s − V c ρ ρ M ′ × + S 1 + 1 M ⋅ ′ L s ( ) ′ V c ρ ρ M ′ × + S 1 （14） = Ke Ts + s − τ 1 ⋅ Heat s ( ) + 其中： K L s ( ) ′× ′ C h = Ke Ts + s − τ 1 Ts + 1 K = Ch M ′ , τ = t ,d T = V c ρρ M ′ （15） 2 神经网络 PID 控制系统设计 2.1 径向基函数神经网络模型 RBF 神经网络是具有 n 个输入、单隐层和一个输出 的 3 层前馈网络，由输入层空间到单隐层空间的映射是 非线性变换，隐层空间到输出空间的映射是线性变换。 该网络具有全局最优、运算量小、运算速度快、以及最 佳逼近性能，且训练方法快速易行，使其在实时控制中 成为可能[4-5]。其结构如图 1 所示。 （12） 1 图 1 径向基函数神经网络结构图 Fig.1 RBF neural network structure 网络输出可表示为式（16）。 m T = w h i i y W H = ∑ （16） 式中，X=[x1,x2,…,xn]T 为 RBF 神经网络的输入向量； W=[w1,w2, … ,wm]T 为 RBF 神 经 网 络 权 矢 量 ； H=[h1,h2,…,hm]T 为径向基矢量,其中 hj 为高斯函数[6]，见 式（17）。 0 h i = exp || − ⎡ ⎢ ⎣ c x − i 2 2 σ i || ⎤ ⎥ ⎦ i ( = 1,2, （17） m ) , 式中，x 是 n 维输入向量；ci 是第 i 个径向基函数的中心， 与 x 具有相同维数的向量；σi 是第 i 个感知变量，它决定 了该基函数围绕中心点的宽度；||x－ci||是向量 x－ci 的范 数，表示 x 与 ci 之间的距离[7]。 神经网络的性能指标函数[8]为式（18）。 J = 1 2 y k ( ( ) − y m k ( )) 2 = 1 2 e k ( ( )) 2 （18） 为了 RBF 网络模型期望输出与实际输出之间的误差 目标函数最小，对输出权，节点中心和节点基宽参数采 用迭代算法见式（19）～（21）。 

第 2 期 屈 毅等：温室温度控制系统的神经网络 PID 控制 309 w k ( ) j = w k ( j [ α + y k ( )] m 2)] − （19） j j 1) − + w k ( y k [ ( ) η − w k 1) ( − − x c || || − 3 σ j [ η σ ασ j || j || + k ( j j （20） m ( k y = − = σ j k ( ) σ ∆ j y k [ ( ) 1) − + ∆ k w h ( )] j ⎧ ⎪ ⎨ ⎪ σ ⎩ j ⎧ ⎪ ⎨ ⎪ ⎩ 式中，η 为学习效率，α 为动量因子，且 η, α∈[0,1]。 x c − 2 σ j [ ασ ji c 1) η − + ∆ k w ( )] y k [ ( ) 1) − − 1) − − σ ji k ( ) σ j 1)] 1)] c ∆ − = − = + − k c k k k c y ( ( ( ( i ji m ji ji ji ji j （21） Jacobian 矩阵反映被控对象的输出对控制量输入变 化的灵敏度，其值可由神经网络辨识而得。取 RBF 网络 的第一个输入为 u(k)，x1=u(k)，则 Jacobian 矩阵的算法见 式（22）。 Y k ( ) ∂ u k ( ) ∂ ∑ j 2.2 RBF- PID 控制系统的设计 w h ∂ ∂∑ j j u k ( ) Y k ( ) ∂ m u k ( ) ∂ w h m m − 2 2 j j （22） ji b x 1 ≈ = = c 1 = 1 = m m ji j RBF- PID 控制器可以克服常规 PID 控制器的不足， 在常规 PID 控制器的基础上利用 RBF 神经网络的自适应 能力，调整控制器的控制参数，构成一个具有自适应能 力的控制器。其结构图如图 2 所示。 图 2 RBF-PID 控制器的结构 Fig.2 RBF-PID control structure 常规 PID 控制器为线性控制器，根据给定值 r(k)与被 控对象实际输出值 y(k)构成的偏差 e(k)进行控制[9]。 = r k ( ) − y k ( ) （23） e k ( ) 控制器输出 u(k) + K e k ( ) u k ( ) = p K e j K e k [ ( ) ( ) + ∑ d i − e k ( − 1)] （24） k j = 0 将偏差的比例、积分和微分通过线性组合构成控制 量，对被控对象进行控制。常规增量式数字 PID 的控制 算法[10]为（式 25）。 K e k [ ( ) − p K e k + − e k [ ( ) 2 ( K e k ( ) i e k ( − 1)] + 1) − + （25） e k ( − u k ( ) ∆ 2)]) = d 参数，实现 PID 控制器参数的在线自整定。该控制器实 质上为一变系数的比例、积分、微分控制器，学习算法 是自适应的，所以本质上是非线性的。控制学习算法见 式（26）。 x x x (1) (2) (3) = = = ⎧ ⎪ ⎨ ⎪ ⎩ − e k ( e k ( ) − e k ( ) e k e k ( ) 2 ( − 1) 1) − + e k ( − 2) （26） PID 控制器参数 Kp、Ki、Kd 的调整采用梯度下降法 见式（27）。 ⎧∆ K ⎪ ⎪ ⎪ ⎪∆ K ⎨ ⎪ ⎪ ⎪ ⎪⎩ K ∆ = − η p p = − η i i J ∂ K ∂ J ∂ K ∂ i J ∂ K ∂ d = − η p p = − η i p = u J Y ∂ ∂ ∂ Y u K ∂ ∂ ∂ J Y u ∂ ∂ ∂ Y u K ∂ ∂ ∂ i J Y u ∂ ∂ ∂ Y u K ∂ ∂ ∂ = η p e k ( ) η i e k ( ) Y ∂ u ∂ = η d e k ( ) Y ∂ u ∂ x (1) x (2) Y ∂ u ∂ x (3) d = − η d d = − η d （27） 式中 ηp、ηi、ηd 分别为比例、积分、微分的学习速率，对 不同的权系数分别进行调整。 3 温室温度控制系统仿真结果分析 在 RBF- PID 整定中，RBF 辨识网络选取 3-6-1 结构， RBF 网络辨识器的输入为 u(k)，y(k)，y(k-1)，输出为 ym(k)， RBF 网络基函数半 σ =0.65，加权系数初值 w1=0.01， w2=0.02，w3=0.01。温度控制系统数学模型的相关参数取 值 1/k′=4356.3，T=856.35，τ =108。经过多次训练试验后， 最终参数选择为学习效率 η=0.32，动量因子 α=0.06，比 例、积分、微分的学习速率 ηp=0.5，ηi =0.45，ηd =0.4。仿 真结果如图 3～5 所示。 图 3 性能指标函数 J 的优化过程 Fig.3 Optimization process of objective function J 式中 Kp、Ki、Kd 分别为比例、积分、微分系数。Kp、Ki、 Kd 视为依赖于系统运行状态的可调整系数。 RBF-PID 控制是将 PID 控制规律融入神经网络之中 的新型控制器，隐含层中含有比例（P）、积分（I）、微分 （D）3 个单元，该控制器利用 RBF 网络辨识器提供的 Jacobian 信息，在线调整 PID 控制器中 kp、ki、kd。3 个 图 4 RBF-PID 控制系统的方波响应 Fig.4 Control system square wave response 

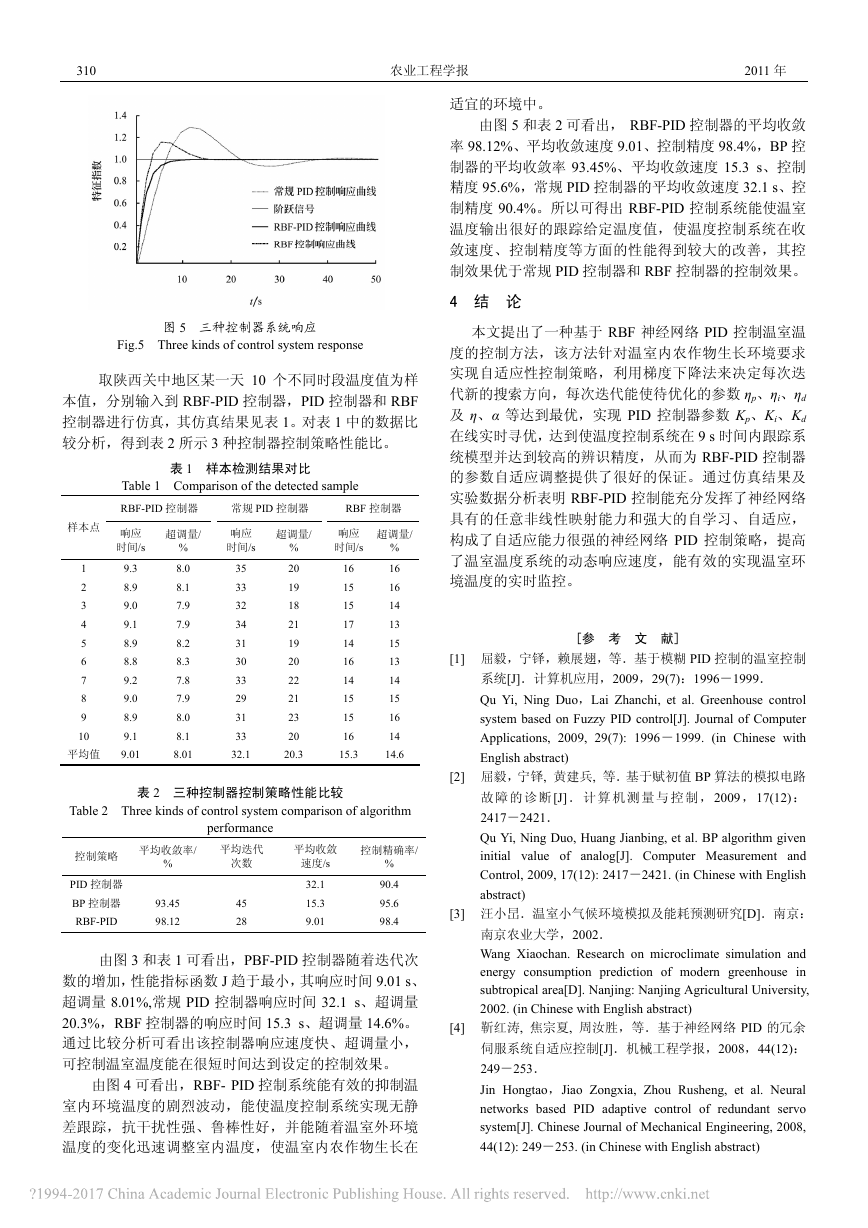
农业工程学报 2011 年 310 适宜的环境中。 由图 5 和表 2 可看出， RBF-PID 控制器的平均收敛 率 98.12%、平均收敛速度 9.01、控制精度 98.4%，BP 控 制器的平均收敛率 93.45%、平均收敛速度 15.3 s、控制 精度 95.6%，常规 PID 控制器的平均收敛速度 32.1 s、控 制精度 90.4%。所以可得出 RBF-PID 控制系统能使温室 温度输出很好的跟踪给定温度值，使温度控制系统在收 敛速度、控制精度等方面的性能得到较大的改善，其控 制效果优于常规 PID 控制器和 RBF 控制器的控制效果。 4 结 论 本文提出了一种基于 RBF 神经网络 PID 控制温室温 度的控制方法，该方法针对温室内农作物生长环境要求 实现自适应性控制策略，利用梯度下降法来决定每次迭 代新的搜索方向，每次迭代能使待优化的参数 ηp、ηi、ηd 及 η、α 等达到最优，实现 PID 控制器参数 Kp、Ki、Kd 在线实时寻优，达到使温度控制系统在 9 s 时间内跟踪系 统模型并达到较高的辨识精度，从而为 RBF-PID 控制器 的参数自适应调整提供了很好的保证。通过仿真结果及 实验数据分析表明 RBF-PID 控制能充分发挥了神经网络 具有的任意非线性映射能力和强大的自学习、自适应， 构成了自适应能力很强的神经网络 PID 控制策略，提高 了温室温度系统的动态响应速度，能有效的实现温室环 境温度的实时监控。 [参 考 文 献] [1] 屈毅，宁铎，赖展翅，等．基于模糊 PID 控制的温室控制 系统[J]．计算机应用，2009，29(7)：1996－1999． Qu Yi, Ning Duo，Lai Zhanchi, et al. Greenhouse control system based on Fuzzy PID control[J]. Journal of Computer Applications, 2009, 29(7): 1996－1999. (in Chinese with English abstract) [2] 屈毅，宁铎, 黄建兵, 等．基于赋初值 BP 算法的模拟电路 故 障 的 诊 断[J] ． 计 算 机 测 量 与 控 制 ，2009 ，17(12) ： 2417－2421． Qu Yi, Ning Duo, Huang Jianbing, et al. BP algorithm given initial value of analog[J]. Computer Measurement and Control, 2009, 17(12): 2417－2421. (in Chinese with English abstract) [3] 汪小旵．温室小气候环境模拟及能耗预测研究[D]．南京： 南京农业大学，2002． Wang Xiaochan. Research on microclimate simulation and energy consumption prediction of modern greenhouse in subtropical area[D]. Nanjing: Nanjing Agricultural University, 2002. (in Chinese with English abstract) [4] 靳红涛, 焦宗夏, 周汝胜，等．基于神经网络 PID 的冗余 伺服系统自适应控制[J]．机械工程学报，2008，44(12)： 249－253． Jin Hongtao，Jiao Zongxia, Zhou Rusheng, et al. Neural networks based PID adaptive control of redundant servo system[J]. Chinese Journal of Mechanical Engineering, 2008, 44(12): 249－253. (in Chinese with English abstract) 图 5 三种控制器系统响应 Fig.5 Three kinds of control system response 取陕西关中地区某一天 10 个不同时段温度值为样 本值，分别输入到 RBF-PID 控制器，PID 控制器和 RBF 控制器进行仿真，其仿真结果见表 1。对表 1 中的数据比 较分析，得到表 2 所示 3 种控制器控制策略性能比。 表 1 样本检测结果对比 Table 1 Comparison of the detected sample RBF-PID 控制器 RBF 控制器 样本点 响应 时间/s 1 2 3 4 5 6 7 8 9 10 平均值 9.3 8.9 9.0 9.1 8.9 8.8 9.2 9.0 8.9 9.1 9.01 超调量/ % 8.0 8.1 7.9 7.9 8.2 8.3 7.8 7.9 8.0 8.1 8.01 超调量/ 常规 PID 控制器 响应 时间/s 35 33 32 34 31 30 33 29 31 33 32.1 % 20 19 18 21 19 20 22 21 23 20 20.3 响应 时间/s 16 15 15 17 14 16 14 15 15 16 15.3 超调量/ % 16 16 14 13 15 13 14 15 16 14 14.6 表 2 三种控制器控制策略性能比较 Table 2 Three kinds of control system comparison of algorithm performance 控制策略 平均收敛率/ PID 控制器 BP 控制器 RBF-PID % 93.45 98.12 平均迭代 次数 45 28 平均收敛 速度/s 32.1 15.3 9.01 控制精确率/ % 90.4 95.6 98.4 由图 3 和表 1 可看出，PBF-PID 控制器随着迭代次 数的增加，性能指标函数 J 趋于最小，其响应时间 9.01 s、 超调量 8.01%,常规 PID 控制器响应时间 32.1 s、超调量 20.3%，RBF 控制器的响应时间 15.3 s、超调量 14.6%。 通过比较分析可看出该控制器响应速度快、超调量小， 可控制温室温度能在很短时间达到设定的控制效果。 由图 4 可看出，RBF- PID 控制系统能有效的抑制温 室内环境温度的剧烈波动，能使温度控制系统实现无静 差跟踪，抗干扰性强、鲁棒性好，并能随着温室外环境 温度的变化迅速调整室内温度，使温室内农作物生长在 

第 2 期 屈 毅等：温室温度控制系统的神经网络 PID 控制 311 [5] Breiman L. Bagging predictors[J]. Machine Learning, 1996, 24(3): 123－140. [6] David West, Scott Dellana, Jingxia Qian. Neural network ensemble strategies for financial decision applications[J]. Computers and Operations Research, 2005, 32(11): 2543－ 2559. [7] 宋文龙，曹军．基于自适应逆控制的干燥窑温度控制方法 研究[J]．农业工程学报，2006，22(3)：95－98． Song Wenlong, Cao Jun. Approach to controlling the temperature of drying kiln using feedback-error-learning based adaptive inverse control[J]. Transactions of the CSAE, 2006, 22(3): 95－98. (in Chinese with English abstract) [8] Hu Hongjie, Er Lianjie, Liu Qiang, et al. Stable and adaptive PID control based on neural network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2001, 27(2): 153 －156. [9] Yuan H B. Research on neural network PID control with application to heavy-duty wheeled vehicle steering system[J]. Journal of System Simulation, 2005, 17(5): 1185－1191. [10] Liu Y H, Li S M. Single neuron PID control based on identification[J]. dynamic RBF neural network on1ine Journal of System Simulation, 2006, 18(2): 804－808. Neural networks based on PID control for greenhouse temperature Qu Yi1, Ning Duo2, Lai Zhanchi1, Cheng Qi1, Mu Lining1 (1. Department of Electrionics and Information Engineering, Xianyang Vocational Technical College, Xianyang 712000, China 2. College of Electric and information Engineering, Shaanxi University of Science and Techonology, Xi′an 710021, China;) Abstract: A mathematical model of greenhouse temperature was established. Confronted with problem of greenhouse temperature control existed in conventional PID controller such as big inertia, big lag, bad adaptive ability and robustness, and other defects, a kind of intelligent PID controller based on RBF neural network with adaptive ability and self-leaning and self-organization was proposed to adjusted the parameters of PID controller. It identified the Jacohian matrix of feedback system by the RBF neural network and acquired on-line tuning the parameters of PID controller. The experimental results demonstrated that a high performance was achieve with little overshoot, steady-state precision and disturbance rejection ability. Key words: greenhouse, neural network, adaptive, mathematic model, temperature control