logo资料库

基于萤火虫算法的装配序列规划研究.pdf

发布时间：2022-06-14 发布人：admin 分类：说明书 资料大小：0.49M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    第 49 卷第 11 期 2 0 1 3 年 6 月 机 械 工 程 学 报 JOURNAL OF MECHANICAL ENGINEERING Vol.49 No.11 2 0 1 3 Jun. DOI：10.3901/JME.2013.11.177 基于萤火虫算法的装配序列规划研究* 曾 冰 李明富 张 翼 马建华 (湘潭大学机械工程学院 湘潭 411105) 摘要：将应用于连续空间优化的萤火虫算法扩展到装配序列规划领域。针对装配序列规划问题的特点，重新定义萤火虫算法 的各种相关操作，提出面向装配序列规划问题的离散萤火虫算法。建立装配体的十进制干涉矩阵，提高干涉矩阵的输入效率。 建立考虑装配序列稳定性、装配方向改变次数以及装配工具变换次数三个评价指标的适应度函数。在适应度函数构造方面， 对传统的装配序列规划研究进行改进，提出更加完善的装配序列稳定性量化方式以及更加合理的装配工具变换次数求解算 法。以一个典型的、包含 19 个零部件的机械臂装配实例分析该算法的特性，验证萤火虫算法的可行性和可靠性；并将萤火 虫算法与在装配序列规划领域应用最广泛的遗传算法进行比较，试验证明萤火虫算法更有效。 关键词：装配序列规划 萤火虫算法 适应度函数 中图分类号：TP24 TP29 TP39 Research on Assembly Sequence Planning Based on Firefly Algorithm ZENG Bing LI Mingfu ZHANG Yi MA Jianhua (School of Mechanical Engineering, Xiangtan University, Xiangtan 411105) Abstract：The firefly algorithm, which is always applied to optimize in continuous space, is extended to assembly sequence planning field. To solve the problem of assembly sequence planning, all sorts of relevant operations of firefly algorithm are redefined, then the discrete firefly algorithm is proposed. To improve the inputting efficiency of the interference matrix, the decimal interference matrix of assembly is created. The stability of sub-assembly, the frequency of assembly direction changes and the frequency of assembly tool changes are taken into account in the fitness function in this paper. To create better fitness function, a better method of quantizing the stability of assembly sequence and a more rational solving scheme of the frequency of assembly tool changes are proposed in this paper. The characteristics of firefly algorithm are showed via an experiment of a typical assembly which contains 19 parts. The experiment proved that firefly algorithm is feasible and reliable. At the same time, the efficiency of firefly algorithm is compared with the efficiency of genetic algorithm which is applied most frequently in assembly sequence planning field. The results of experiment show that the firefly algorithm is more efficient than genetic algorithm. Key words：Assembly sequence planning Firefly algorithm Fitness function 0 前言 配建模、装配序列规划以及装配路径规划这三个部 分工作。装配序列规划是装配规划的核心，它的优 劣直接关系到产品的装配成本。在传统的装配系统 产品的装配是产品制造过程的最后环节，装配 中，产品的装配序列通常由工程师凭借其经验确定， 质量从很大程度上影响产品的性能，在制造成本中， 然而，当产品比较复杂时，工程师需要花大量的时 装配成本占有很大的比例。据统计，装配成本在制 造成本中的比重超过 40%，装配工作量占产品制造 工作总量的 20%～70%[1]。因此装配规划在产品设 计开发过程中占有很重要的地位。装配规划包括装 * 湖南省教育厅科研(12C0396)、湖南省自然科学基金委员会与湘潭市 政府自然科学联合基金重点(12JJ8010)和湖南科技大学机械设备健康 维护湖南省重点实验室开放基金(201205)资助项目。20120926 收到初 稿，20130314 收到修改稿 间来确定其装配序列，并且装配序列不一定是可行 装配序列或最优装配序列。因为产品的装配序列数 量与产品的零部件数量呈指数增长关系，所以复杂 产品的装配序列规划很容易遇到装配序列组合爆炸 问题[2]。因此，以图论为基础的传统搜索方法难以 求解复杂产品的最优装配序列。近 20 年来广大研究 者开始将现代智能优化计算方法应用到装配序列规
    178 机 械 工 程 学 报 第 49 卷第 11 期期 划领域中来，如遗传算法、蚁群算法、模拟退火算 法和粒子群算法等，为复杂产品的装配序列求解提 供了强有力的方法。 遗传算法因其具有全局搜索和梯度信息不依 赖的寻优能力，使其在很多组合优化问题中得到广 泛应用，包括装配序列规划问题[3-7]。但是，遗传算 法对初始种群的质量和大小依赖性较强，要求初始 种群中的可行装配序列的比例较大，可行装配序列 需要人工设定，耗时较大；初始种群中不合适的装 配序列往往可能引导搜索过程向差的方向进化，最 终可能得不到最优装配序列，甚至有可能不收敛[8]。 蚁 群 算 法 在 装 配 规 划 领 域 也 有 着 广 泛 的 应 用 ， WANG 等[9]对蚁群算法进行了深入的研究。蚁群算 法在进行装配序列规划时需要指定基础零件；并且 信息素残留系数和转移概率公式中参数选择难度较 大，算法的收敛速度不理想，容易陷入局部最优 解[10]。模拟退火算法来源于金属加工中的退火过 程，在装配规划领域得到了广泛的应用[11]。由于模 拟退火算法对解空间的拓展不够好，不容易搜索到 最有效的区域，所以搜索效率不是很好；并且，在 最优装配序列的选择运算过程中，模拟退火算法是 通过对装配序列的目标函数进行评价，剔除大量不 可行的装配序列，存储所得到的最优解。这种算法 初始序列的选取方法比较麻烦，且需要剔除大量不 可行的装配序列，种群多样性差，难以得到最优装 配序列。 萤火虫算法是群集智能优化算法领域的最新 算法，试验表明，萤火虫算法在寻找各种全局最优 解上比遗传算法等更有效，成功率更高，在解决 NP 难度问题上有着巨大的潜力[12-14]。萤火虫算法在一 些组合优化问题的求解中已获得了成功的应用，比 如路径规划[15]。目前还少见学者将萤火虫算法应用 于装配序列规划领域，正因为萤火虫算法在解决组 合优化问题领域的巨大潜力，本文针对装配序列规 划问题，提出了离散萤火虫算法，最后利用此算法 获得装配实例的最优或近优装配序列，并和遗传算 法进行了比较。 萤火虫算法的执行基于以下三种原则。 (1) 所有的萤火虫没有性别之分。 (2) 吸引力与它们的亮度成正比。对于任意两 个闪光的萤火虫，亮度较弱的一方将飞向亮度较强 的一方。并且吸引力与萤火虫之间的距离和空气光 照吸收率亦有关，距离或者光照吸收率的增加都会 降低吸引力。如果没有比当前萤火虫更亮的萤火虫， 则当前萤火虫将随机移动。 (3) 萤火虫的亮度由适应度所决定。任意两个 萤火虫 i 和 j 分别在位置 Xi 和 Xj 之间的距离是笛卡 尔距离 r ij  X i  X j  式中 d——坐标维数 d  x i k ,  k 1  x j k , 2 (1) xi,k——空间坐标 Xi 的第 k 维分量 xj,k——空间坐标 Xj 的第 k 维分量 萤火虫的吸引力定义如下   r   (2) 式中 β0——萤火虫之间的距离 r = 0 时的吸引力， exp r    0 一般取 1 即可  2  γ——光照吸收率，理论取值范围是[0,∞) 萤火虫 i 按照如下公式向吸引力更强的萤火虫 j 移动 t 1 x   i k , t x i k ,   0 exp  2 r   式中 ——待定参数  x t j k ,  t x i k ,     rand 0.5   (3) rand——0 到 1 之间的随机数 标准萤火虫算法的解空间属于连续的实数域 空间，而装配序列规划问题的解空间属于离散的整 数域空间，并且每一维的整数值互不相同。为了使 面向连续优化问题的萤火虫算法适用于求解装配序 列规划问题，一方面可以对装配序列规划问题进行 改进，使其适应于萤火虫算法的优化；另一方面可 以对萤火虫算法进行相应改进，使其适应于装配序 列规划，本文采用后一种方法。 1 标准萤火虫算法原理 2 几何可行性推理 萤火虫可以通过感知有效范围内其他萤火虫 发光的强度和频率来确定其他个体的存在和吸引 力，从而达到吸引异性和猎物的目的。英国剑桥大 学工程系的 YANG[13-15]在 2009 年根据萤火虫的这 种行为提出了萤火虫算法。 在空间直角坐标系中，零件装配方向一般分为 d(k)={+x,–x,+y, –y,+z, –z}={dk}六个方向。由于文中 没有进行干涉矩阵的自动生成，干涉矩阵的输入方 式为手动输入，为了提高干涉矩阵的输入效率，求 得零件的装配方向，建立装配体的十进制干涉矩阵
    月 2013 年 6 月 曾 冰等：基于萤火虫算法的装配序列规划研究 179 I 10  I  i j n n  式中，Iij 为零件 Pj 沿坐标轴各正方向装配时与零件 Pi 的干涉值的集成表示，取值情况如下所示 I ij = 0 1 2 3 4 5 6 7              没有干涉 仅在 方向上发生干涉 仅在 方向上发生干涉 在 、 方向上均发生干涉 仅在 方向上发生干涉 在 、 方向上均发生干涉 z  y  y z   x  x z   x y   y x   在 、 方向上均发生干涉 在 、 、 方向上均发生干涉  z 因为零件 Pj 沿坐标轴各负方向装配时与零件 Pi 的干涉情况，与零件 Pi 沿坐标轴相应的正方向装 配时与零件 Pj 的干涉情况相同，所以只需要将装配 体沿坐标轴正方向的十进制干涉矩阵转置即可得到 装配体沿坐标轴负方向的十进制干涉矩阵。 (4) 靠性、夹具和工具的复杂性。在传统的装配序列稳 定性量化过程中，各研究者往往只考虑连续装配的 两个零件之间的连接关系，例如文献[3]，而本文的 装配序列稳定性量化过程中，不仅考虑当前装配零 件与前一装配零件之间的连接关系，也考虑了与之 前所有装配好的零件之间的连接关系，量化效果更 为完善，更接近实际工程。 为了对可行装配序列的装配稳定性进行量化 表示，建立装配体的连接矩阵  L ，其中 lij 表示零件 Pj 和零件 Pi 之间的连接关系。稳定性量化 准则如下所示。 ij n n l  (1) 当零件 Pj 和零件 Pi 之间存在稳定连接关 系，并且 Pi 用夹具保持稳定更好时；或者 Pj 仅在重 力作用下能够稳定保持在 Pi 上时，lij = 2。 (2) 当零件 Pj 和零件 Pi 之间存在稳定连接关 系，并且 Pj 用夹具保持稳定更好时，lij = 1。 (3) 当零件 Pj 和零件 Pi 之间不存在连接关系 现定义 Vk(Pi)(k=1,2,…,6)为零件 Pi 沿 dk 方向装 配时与已装配好的各零件之间的干涉值之和，若 Vk(Pi) = 0，则表示零件 Pi 可沿 dk 方向进行装配；若 Vk(Pi)≠0，则零件 Pi 不可沿 dk 方向装配。表达式 如下 时，lij = 0。 这里的稳定连接是指两个零件之间通过紧固 件联接或者孔轴之间的过盈联接等具有强制约束零 件之间的联接。一个装配序列的稳定性指标 Vs 的量 化表示为 (5) V s =  0 S i n i  2  sV  2 n 2  (6)  V P k i    d k P P j i I i 1  j 1  由此干涉矩阵，可以求得零件 Pi 的可行装配方 向集为 Df (Pi)={ dk∣Vk(Pi)=0}。 3 适应度函数的构造 对 于 一 个 装 配 序 列 {P1,P2, … ,Pn} ， 若 6 恒成立，则{P1,P2,…,Pn}为可行装  V P k i 1  0 ，则序列{P1,P2, …,Pn}      n        1 k i  V P k i 1 配序列；若 不可行。  0       n     6   1 k i 在装配序列规划领域，适应度函数所考虑的因 素主要是装配序列稳定性、装配方向改变次数以及 装配工具变换次数，本文也是从这三方面来构造适 应度函数。对于任意一个可行装配序列，这三个评 价指标的数学模型构建如下。 3.1 装配序列的稳定性 装配序列的稳定性是指每个装配操作所涉及 的零件与子装配体或者两个子装配体在重力和建立 装配所需力的作用下，保持各自内部装配关系的能 式中，n 为装配序列中零件的总个数，Si 为零件 Pi 的装配稳定性，如果 lji (1≤j≤i–1)中有等于 2 的元素， 则 Si=2；如果没有等于 2 的元素，但有等于 1 的元 素，则 Si=1；如果所有元素都等于 0，则 Si=0。 显然，Vs 越大，产品装配序列的装配稳定性就 越好。 3.2 装配方向的改变次数 装配方向的改变会增加装配设备运动代价，从 而增加装配成本，所以产品的装配应尽可能减少装 配 方 向 的 变 更 。 对 于 任 意 可 行 装 配 序 列 {P1,P2, …,Pn}，此装配序列的最小装配方向改变次 数 Vd 的求解步骤如下所示。 (1) 令 i = 0，m = 1，Vd= 0。  D P (2) 若 i D P     ( f i f i m   i i m   i  表示 i, i+1,…, i f 1    D P  i+m 号 零 件 可 行 装 配 方 向 集 的 交 集 ) ， 但 i m    ，那么装配零件 Pi+m+1 时需要改变装 i 配方向，令 Vd = Vd +1，跳至步骤(3)；否则，令 m = m+1，如果 i + m +1 < n，重复执行步骤(2)；否则， 跳至步骤(4)。 (3) 令 i = i + m +1，m = 1，如果 i < n，跳至步 力的总和。装配序列的稳定性体现了装配操作的可 骤(2)；否则，跳至步骤(4)。
    180 机 械 工 程 学 报 第 49 卷第 11 期期 (4) 结束。 显然，Vd 越小，装配方向改变次数越小，装配 4.1 离散萤火虫算法的相关操作 在装配序列空间中，离散萤火虫算法的相关操 成本越低。 3.3 装配工具变换次数 产品的装配应尽可能减少装配工具的更换次数， 以提高装配效率。在传统的装配工具变换次数建模 中，每个零件只给定一种装配工具[16]，但在实际工程 中，很多零件涉及多种装配工具，本文考虑了零部件 有多种装配工具的情况，因此本文的装配工具变换次 数建模更符合实际工程。装配规划之初通过预先定义 每个零件的装配工具集合 Tf (Pi)，从而对一个给定的 装配序列，其对应的最佳装配工具序列也随之确定。 类似求解序列装配方向改变次数的步骤，装配序列的 装配工具改变次数 Vt 求解步骤如下所示。 (1) 令 i = 0，m = 1，Vt= 0。  T P (2) 若 f i T P  f (    i i m   i i m   i  表示 i, i+1,…,     T P f i i+m 号 零 件 装 配 工 具 集 合 的 交 集 ) ， 但 i m 1    ，那么装配零件 Pi+m+1 时需要改变装 i 配工具，令 Vt = Vt +1，跳至步骤(3)；否则，令 m = m+1，如果 i + m +1 < n，重复执行步骤(2)；否则， 跳至步骤(4)。 (3) 令 i = i + m +1，m = 1，如果 i < n，跳至步 骤(2)；否则，跳至步骤(4)。 (4) 结束。 显然，Vt 越小，装配工具的更换时间就越少， 装配效率就越高。 根据上述分析，对各评价指标进行加权确定适 应度函数，如下 f = + V t 2 V +      d 1 3    n 1 4    2 n V   s 2  装配序列可行 装配序列不可行 式中，ω1，ω2，ω3 为各评价标权重系数。 (7) 在本文中，适应度越小表示萤火虫亮度越大， 即装配序列更好。 4 离散萤火虫算法的相关操作及步骤 由于标准萤火虫算法不适用于装配序列规划 问题的求解，本文提出了离散萤火虫算法用于装配 序列规划问题的求解，重新构造萤火虫位置更新公 式如下 t 1 x   i k , t x i k ,  0 exp   2 r   ij    x t j k , x t  i k ,    rand 0.5  (8) 作定义如下。 (1) 萤火虫 i 的位置：为了表示某一产品装配序 列的位置，这里采用一种特殊的编码方式，将每个 萤火虫的位置初始化为一个 n 维矢量，每一个萤火 虫的位置对应一个装配序列，萤火虫 i 用如下装配 序列来编码  x i 式中 n——萤火虫 i 的维数或产品的零部件总数   x , , i n ,  (9)  1,2,  n x i j , x i j , X x i    ,2 ,1 , , , , T i xi,j ——萤火虫 i 的第 j 维元素 矢量 Xi 中任意两个元素互不相等。为了保证种 群的多样性，加强算法的全局搜索能力，初始装配 序列是随机生成的。 (2) 位置间的减法操作( t t j iX X )：位置间的减 iS ， 1t+ iS t j  S Θ t+ 1 i t X X i 法操作是用来得到萤火虫 i 的主移动方向 1t+ 的表示如下 (10) 在运算过程中，逐个比较装配序列 t jX 和 t iX 的 k n t   维元素 1 i ks  ，如果 , iS 从矢量 t jX i kX ， iS 的第  1k t x j k , 各维数值，对 1t+ t t i kx 不相等， 1 j kx 和 , s t   ，即矢量 1t+ i k , , t 的相应维数上继承有效的元素；如果 , t i ks   。 ,  0 (3) 方向的数乘操作：在标准萤火虫算法中， (取值在 0 到 1 之间)是步长，即用来控 2 ijr  0 exp  j kX =  t , 1 制萤火虫 i 向萤火虫 j 沿方向 1t +S 移动的距离。本文 i 定义 1t +_S 来表示 1t +S 与 i i +1 _S t i  2 ijr  的乘积，如下   +1 S t i (11)  2 ijr   0 exp   2 ijr  0 exp   0 exp  在本文中， 和(8)式中的第三部分 i_S 从矢量 1t+ α|rand–0.5|被联合用来控制矢量 中继承元素的数量。方向的数乘操作公式如下所示 iS 1t+ S _ t +1 i k , =     S t +1 i k , 0  rand 0.5 < exp   0 其他  r   ij 2 (12) 显然， 2 ijr  1t+ iS 中继承的元素越多。 0 exp   越大，矢量 1t+ i_S 从矢量 (4) 位置和方向的加法操作：在本文中，离散 萤火虫算法的位置更新主要部分就是萤火虫 i 在 t 时刻的位置矢量和 t+1 时刻的方向矢量之和， 如下所示
    月 2013 年 6 月 曾 冰等：基于萤火虫算法的装配序列规划研究 181 t+ 1 i  X t i  t+ 1 _S i X (13) 在更新萤火虫的位置时，若方向矢量 1t+ i_S 中的 ,_ t 元素 1 i ks  =0，则不改变位置矢量 1t+ iX 中对应第 k 位 t t t i kx 相等；若 1 上的零件号，即 1 i kx  与 , i ks   ，则矢 0 ,_ , ,_ t t i kx 与 1 i ks  交 换 后 量 1t+ iX 第 k 位 上 的 零 件 号 是 , 的值。 4.2 算法步骤 本文提出的离散萤火虫算法的执行步骤如下 所示。 (1) 初始化萤火虫算法相关参数β0、γ、α，给 定群体规模 N，产生初始群体，同时找出适应度最 小的萤火虫个体记为 b，适应度记为 F。 (2) 在每只萤火虫的可见范围内，使该萤火虫 向适应度最小的萤火虫移动，并更新它的适应度， 直到每只萤火虫都完成一次移动，即完成一次迭代。 记录下本次迭代的平均适应度和最优适应度，最优 适应度萤火虫记为 i，其适应度记为 fmin，如果 fmin < F，则令 b= i，F = fmin。 (3) 若满足结束条件则停止迭代，输出最优萤 火虫个体 b，最优适应度 F 以及各代最优适应度和 平均适应度；否则，令迭代变量 it = it + 1，跳至步 骤(2)。 5 实例对比分析 5.1 基于萤火虫算法的装配序列规划试验 应用上述离散萤火虫算法，在 Visual C++ 6.0 环境下编写了基于萤火虫算法的装配序列规划应用 程序。试验时，运行本应用程序的计算机 CPU 型号 是 Intel 酷睿 i5430，CPU 主频范围为 2.27～2.53 GHz，内存为 4 GB，所使用的是 Windows7 64 位操 作系统。下面以包含 19 个零部件的某机械臂为例进 行装配序列规划，该机械臂装配体视图如图 1 所示， 装配体各零件的装配工具集合如表 1 所示。 针对该机械臂的装配，权值 ω1=0.29，ω2=0.18， ω3=0.53。经过多次对比测试，得出：当 β0=1， γ=0.004 8，α=1.4 时，算法的寻优能力和收敛性接 近最佳状态。γ 或 α 取值越小，算法收敛的越快， 取值过小会导致收敛到局部最优解；γ 或 α 取值越 大，算法收敛的越慢，取值过大，会导致算法寻优 能力差或者算法根本不会向最优值收敛。 在离散萤火虫算法各参数和目标函数各权重 系数取值一定的情况下，本文针对种群容量分别取 20、60、100 和 160 时进行了试验，不同种群容量 算法单次迭代 200 代，分别运行 50 次，各次最优适 应度的分布情况如图 2 所示，各次最优装配序列规 划结果如表 2 所示。 图 1 机械臂装配图 表 1 零件装配工具集合 零件位置 装配工具集合 P1 P2 P3 P4 P5 P6 P7 P8 P9 P10 P11 P12 P13 P14 P15 P16 P17 P18 P19 T2 T1 T1、T2 T1 T1 T1 T1 T1 T1 T1、T2 T3 T3 T1 T1 T1 T1 T3 T1 T1、T2 图 2 各次局部最优适应度的分布情况
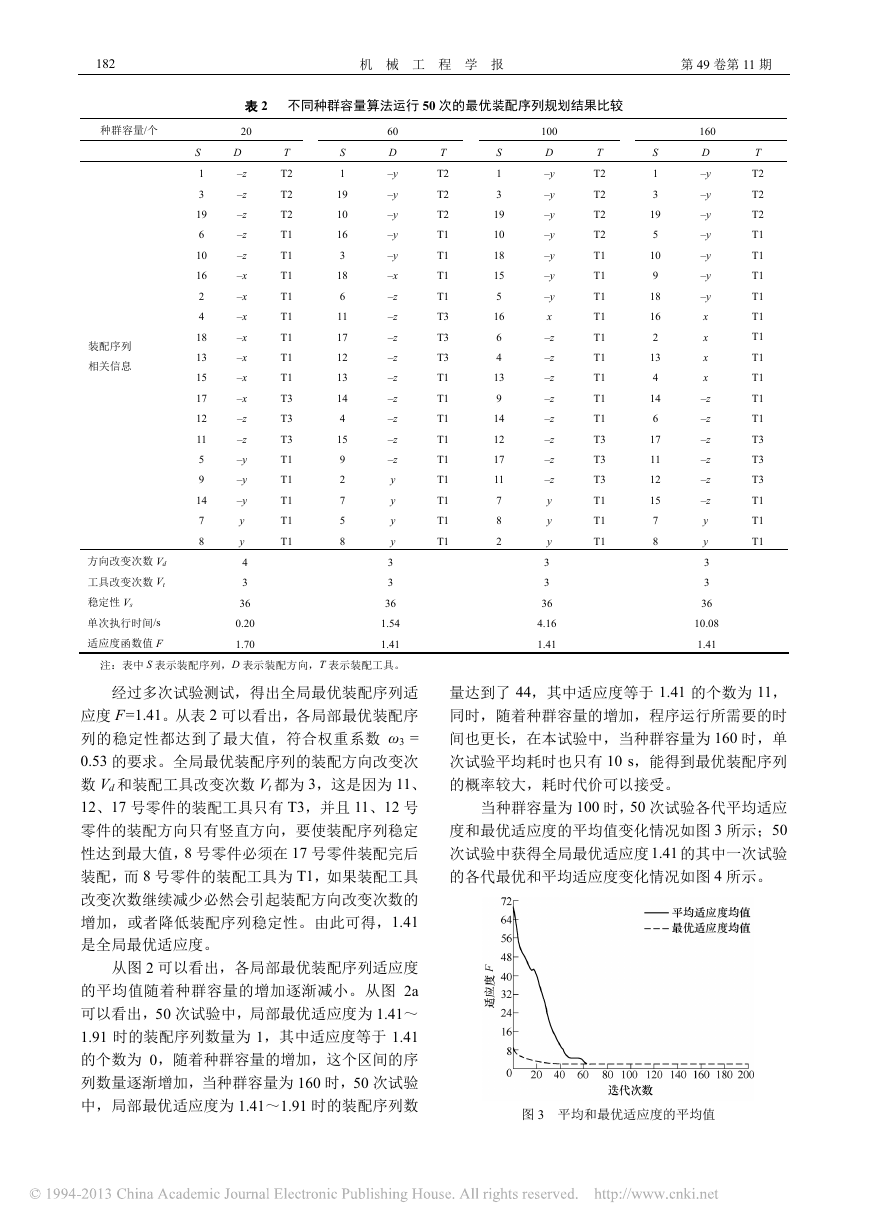
    182 机 械 工 程 学 报 第 49 卷第 11 期期 表 2 不同种群容量算法运行 50 次的最优装配序列规划结果比较 种群容量/个 20 S 1 19 10 16 3 18 6 11 17 12 13 14 4 15 9 2 7 5 8 T T2 T2 T2 T1 T1 T1 T1 T1 T1 T1 T1 T3 T3 T3 T1 T1 T1 T1 T1 60 D –y –y –y –y –y –x –z –z –z –z –z –z –z –z –z y y y y 3 3 36 1.54 1.41 注：表中 S 表示装配序列，D 表示装配方向，T 表示装配工具。 S D –z 1 –z 3 –z 19 –z 6 –z 10 –x 16 –x 2 –x 4 –x 18 –x 13 –x 15 –x 17 –z 12 –z 11 –y 5 –y 9 –y 14 y 7 y 8 4 3 36 0.20 1.70 装配序列 相关信息 方向改变次数 Vd 工具改变次数 Vt 稳定性 Vs 单次执行时间/s 适应度函数值 F 经过多次试验测试，得出全局最优装配序列适 应度 F=1.41。从表 2 可以看出，各局部最优装配序 列的稳定性都达到了最大值，符合权重系数 ω3 = 0.53 的要求。全局最优装配序列的装配方向改变次 数 Vd 和装配工具改变次数 Vt 都为 3，这是因为 11、 12、17 号零件的装配工具只有 T3，并且 11、12 号 零件的装配方向只有竖直方向，要使装配序列稳定 性达到最大值，8 号零件必须在 17 号零件装配完后 装配，而 8 号零件的装配工具为 T1，如果装配工具 改变次数继续减少必然会引起装配方向改变次数的 增加，或者降低装配序列稳定性。由此可得，1.41 是全局最优适应度。 T T2 T2 T2 T1 T1 T1 T1 T3 T3 T3 T1 T1 T1 T1 T1 T1 T1 T1 T1 S 1 3 19 10 18 15 5 16 6 4 13 9 14 12 17 11 7 8 2 100 D –y –y –y –y –y –y –y x –z –z –z –z –z –z –z –z y y y 3 3 36 4.16 1.41 T T2 T2 T2 T2 T1 T1 T1 T1 T1 T1 T1 T1 T1 T3 T3 T3 T1 T1 T1 S 1 3 19 5 10 9 18 16 2 13 4 14 6 17 11 12 15 7 8 T T2 T2 T2 T1 T1 T1 T1 T1 T1 T1 T1 T1 T1 T3 T3 T3 T1 T1 T1 160 D –y –y –y –y –y –y –y x x x x –z –z –z –z –z –z y y 3 3 36 10.08 1.41 量达到了 44，其中适应度等于 1.41 的个数为 11， 同时，随着种群容量的增加，程序运行所需要的时 间也更长，在本试验中，当种群容量为 160 时，单 次试验平均耗时也只有 10 s，能得到最优装配序列 的概率较大，耗时代价可以接受。 当种群容量为 100 时，50 次试验各代平均适应 度和最优适应度的平均值变化情况如图 3 所示；50 次试验中获得全局最优适应度1.41 的其中一次试验 的各代最优和平均适应度变化情况如图 4 所示。 从图 2 可以看出，各局部最优装配序列适应度 的平均值随着种群容量的增加逐渐减小。从图 2a 可以看出，50 次试验中，局部最优适应度为 1.41～ 1.91 时的装配序列数量为 1，其中适应度等于 1.41 的个数为 0，随着种群容量的增加，这个区间的序 列数量逐渐增加，当种群容量为 160 时，50 次试验 中，局部最优适应度为 1.41～1.91 时的装配序列数 图 3 平均和最优适应度的平均值
    月 2013 年 6 月 曾 冰等：基于萤火虫算法的装配序列规划研究 表 3 萤火虫算法和遗传算法的试验结果对比 萤火虫算法 100 60 200 200 遗传算法 100 60 200 200 160 200 20 200 参数 种群容量 20 迭代次数 200 183 160 200 50 程序运行 次数 可行装配 序列的 个数 程序运行 时间/s 最优装配 序列的适 应度函 数值 50 50 50 50 50 50 50 6 25 40 48 50 50 50 50 35 162 458 986 10 77 208 504 4.36 2.65 1.77 1.41 1.7 1.41 1.41 1.41 图 4 最优和平均适应度 从图 3 可以看出，当种群容量为 100 时，50 次 试验中，第 0 代平均适应度均值为 69.877 7，而最 大适应度为 72，可见每次试验初始可行装配序列不 多，因此，该算法对初始装配序列的可行性没有依 赖性。而且从图 3 中可以看出，最优适应度均值和 平均适应度均值随着迭代次数的增加均稳步下降， 可见该算法的稳定性很好。从图 4 可以明显看出， 平均适应度均值在局部有增大现象，这是因为一个 遗传算法得到更小的适应度函数值，萤火虫算法在 种群容量取 60 时就能得到全局最优适应度函数值 1.41，而遗传算法需在种群容量足够大时才能得到 最优适应度函数值，可见遗传算法对初始装配序列 的质量和数量依赖较大。并且，在种群容量相同的 情况下，萤火虫算法程序的运行时间要明显少于遗 萤火虫在飞向另一个萤火虫时，它的适应度可能会 传算法程序的运行时间，可见萤火虫算法的效率要 增大或者可能得到一条不可行装配序列，导致平均 适应度局部增大，这正是种群多样性的体现，增大 明显高于遗传算法。由此可见，萤火虫算法在性能 和效率上都明显好于遗传算法。 了萤火虫得到更好位置的概率，但平均适应度均值 值得说明的是，本文没有把螺栓、螺钉、卡簧 在全局下降的趋势不会改变，在较好参数配置下， 最终会收敛到最优解。 5.2 萤火虫算法与遗传算法的试验对比分析 为了验证萤火虫算法的有效性和优越性，现将 萤火虫算法与在装配序列规划领域应用最广泛的遗 传算法进行比较。为了比较两种算法，仍对相同的 装配实例进行装配序列规划。适应度函数以及各评 价指标权重系数取值保持不变；基于遗传算法的装 配序列规划应用程序同样是用 Visual C++ 6.0 编写， 程序运行环境保持不变。 针对该装配体实例，经过多次对比试验，当交 叉概率为 0.95，变异概率为 0.9 时，遗传算法的寻 优能力和效率接近最佳状态。初始种群随机生成， 针对种群容量分别取 20、60、100 和 160 进行了 试验。 萤火虫算法和遗传算法的试验结果对比如表 3 所示。 从表 3 可以看出，无论种群容量取 20、60、100 或者 160，在 50 次程序运行后，萤火虫算法每次都 能得到可行装配序列，而遗传算法当种群容量较小 时，50 次试验得到可行装配序列的次数较少，随着 种群容量的增加，得到可行装配序列的次数会逐渐 增加；在种群容量相同的情况下，萤火虫算法能比 等紧固件作为装配序列中的零件，因为这些紧固件 的装配是由它们所连接的零部件的装配所决定的， 在实际自动化装配中，对于这些紧固件是采用并行 装配的方式，所以本文不考虑这些紧固件得出的装 配序列更接近工程实际情况，特别是对大型复杂装 配体的装配。 另外，在本文的萤火虫算法装配序列规划应用 程序中，可以指定基准零件来提高算法的运行效率 和收敛速度。但本文的试验是在没有指定基准零件 的基础上进行的。 6 结论 (1) 针对装配序列规划问题的特点，对基本萤 火虫算法的各个操作重新定义，提出了面向装配序 列规划问题的离散萤火虫算法。 (2) 提出了更加完善的装配序列稳定性量化方 式以及更加合理的装配工具变换次数求解算法。 (3) 试验证明，不同于遗传算法等，基于萤火 虫算法的装配序列规划对初始装配序列的可行性和 质量完全没有依赖性，即使初始装配序列全部不可 行，算法也能向全局最优适应度收敛。但萤火虫种
    184 机 械 工 程 学 报 第 49 卷第 11 期期 群容量的大小对算法性能的影响比较明显，种群容 量越大，算法越容易收敛到全局最优适应度。 (4) 试验证明，基于萤火虫算法的装配序列规 划方法是一种行之有效的方法，该算法简单、收敛 速度快、稳定性好，能得到高质量、可靠性强的装 配序列结果。 参 考 文 献 [1] SHAN Hongbo，LI Shuxia，GONG Degang，et al. Genetic simulated annealing algorithm-based assembly sequence planning[C]//International Technology and Innovation Conference，2006 (ITIC 2006)，CP. Advanced Manufacturing Technology，2006：1573-1579. [2] WANG Y，LIU J H，LI L S. Assembly sequence merging based on assembly unit partitioning[J]. Int. J. Adv. Manuf. Technol.，2009，45：808-820. [3] LAZZERINI B，MARCELLONI F. A genetic algorithm for generation optimal assembly plans[J]. Artificial Intelligence in Engineering，2000，14 (4)：319-329. [4] CHEN R S，LU K Y，YU S C. A hybrid genetic algorithm approach on multi-objective of assembly planning problem[J]. Engineering Applications of Artificial Intelligence，2002，15：447-457. [5] 赵磊，李原，余剑峰. 支持变约束的装配顺序随需式 规划方法[J]. 机械工程学报，2011，47(5)：149-155. ZHAO Lei，LI Yuan，YU Jianfeng. Assembly Sequence Concomitant Planning Method Based for the Variation of Constraint[J]. Journal of Mechanical Engineering，2011， 47(5)：149-155. [6] ROMEO M M ，LEE H L ，KAZEM A. A genetic algorithm for the optimisation of assembly sequences[J]. Computers & Industrial Engineering，2006，50：503-527. [7] ROMEO M M ，LEE H L ，KAZEM A. Assembly sequence planning and optimization using genetic algorithms[J]. Applied Soft Computing，2003，2/3F： 223-253. [8] 于嘉鹏，王成恩，王健熙. 基于最大-最小蚁群系统的 装 配 序 列 规 划[J]. 机 械 工 程 学 报 ，2012 ，48(23) ： 152-166. YU Jiapeng，WANG Chengen，WANG Jianxi. Assembly sequence planning based on max-min ant colony system[J]. Journal of Mechanical Engineering，2012， 48(23)：152-166. [9] WANG Junfeng，LIU Jihong，ZHONG Yifang. A novel ant colony algorithm for assembly sequence planning[J]. Advanced Manufacturing Technology，February，2004： 1137-1143. [10] 史士财，李荣，付宜利，等. 基于改进蚁群算法的装 配序列规划[J]. 计算机集成制造系统，2010，16(6)： 1189-1194. SHI Shicai，LI Rong，FU Yili，et al. Assembly sequence planning based on improved ant colony algorithm [J]. Computer Integrated Manufacturing System ，2010 ， 16(6)：1189-1194. [11] MILNER J M，GRAVES S C，WHITNEY D E. Using least-cost assembly to select simulated annealing sequences[C]// Proceedings of International IEEE Conference on Robotics and Automation，May 8-13， 1994，San Diego，CA. Los Alamitos：IEEE Comput. Soc. Press，1994：2058-2063. [12] YANG X S．Firefly algorithms for multimodal optimization [C]//Proc. of the 5th International Conference on Stochastic Algorithms：Foundations and Applications，2009. Berlin： Springer-Verlag，2009：169-178． [13] YANG X S. Firefly algorithm ， stochastic test functionsand design optimisation[C]//Int. J. Bio-Inspired Computation，March，2010. London：Springer，2010： 78-84. [14] YANG X S. Firefly algorithm，L´evy flights and global optimizatio[C]//Research and Development in Intelligent Systems XXVI，March，2010. London：Springer，2010： 209-218. [15] 刘鹏，刘弘，郑向伟，等. 基于改进萤火虫算法的动 态 自 动 聚 集 路 径 规 划 方 法[J]. 计 算 机 应 用 研 究 ， 2011，28(11)：4146-4149. LIU Peng，LIU Hong，ZHEN Xiangwei，et al. Approach for dynamic group automatic aggregation path planning based on improved FA[J]. Application Research of Computers，2011，28(11)：4146-4149. [16] 王丰产，孙有朝，李娜. 多工位装配序列粒子群优化 算法[J]. 机械工程学报，2012，48(9)：155-162. WANG Fengchan，SUN Youzhao，LI Na. Multi station assembly sequence planning based on particle swarm optimization algorithm [J]. Journal of Mechanical Engineering，2012，48(9)：155-162. 作者简介：曾冰，男，1987 年出生。主要研究方向为现代智能算法和装 配序列规划。 E-mail：zengbing151@163.com 李明富，男，1979 年出生，博士，讲师，硕士研究生导师。主要研究方 向为智能机器人、机器视觉、机械测试和虚拟现实。 E-mail：limingfu2001@foxmail.com
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料