南邮应用物理学计算物理实践报告.docx-资料库

29fd8721-ecac-4379-963c-885f39cc2b8d.docx.pdf-第1页.png

第1页 / 共29页

29fd8721-ecac-4379-963c-885f39cc2b8d.docx.pdf-第2页.png

第2页 / 共29页

29fd8721-ecac-4379-963c-885f39cc2b8d.docx.pdf-第3页.png

第3页 / 共29页

29fd8721-ecac-4379-963c-885f39cc2b8d.docx.pdf-第4页.png

第4页 / 共29页

29fd8721-ecac-4379-963c-885f39cc2b8d.docx.pdf-第5页.png

第5页 / 共29页

29fd8721-ecac-4379-963c-885f39cc2b8d.docx.pdf-第6页.png

第6页 / 共29页

29fd8721-ecac-4379-963c-885f39cc2b8d.docx.pdf-第7页.png

第7页 / 共29页

29fd8721-ecac-4379-963c-885f39cc2b8d.docx.pdf-第8页.png

第8页 / 共29页

南京邮电大学实验报告课程名称：计算物理实践应用物理学专学姓业：号：名：完成日期：

目录第一章简单物理实验的模拟及数据处理................................................................ 1 1.1 问题描述： .................................................... 1 1.2 单摆运动原理 .................................................. 1 1.3 单摆运动模型 .................................................. 2 1.4MATLAB 仿真 .................................................... 2 第二章方程组的数值解法 ................................. 4 2.1 问题描述 ...................................................... 4 2.2 二分法简介 .................................................... 4 2.3 二分法编程原理 ................................................ 4 2.4 MATLAB 仿真结果 ............................................... 5 第三章静电场问题的计算................................................................................................... 7 3.1 问题描述： .................................................... 7 3.2 有限差分法解电磁场的边值问题 .................................. 7 3.2.1 有限差分法简介 ............................................ 7 3.2.2 有限差分法的求解步骤 ...................................... 7 3.2.3 金属槽点位问题有限差分法分析 .............................. 8 3.3 数学模型建立及 MATLAB 求解 .................................... 10 3.3.1 数学模型的建立 ........................................... 10 第四章热传导和波动方程的差分解法 ...................... 12 4.1 问题描述 ..................................................... 12 4.2 波动方程简介 ................................................. 12 4.3 一维波动方程的差分解法 ....................................... 13 4.4 MATLAB 求解与绘图 ............................................ 16 第五章蒙特卡罗方法的了解........................................................................................... 18 5.1 问题描述 ..................................................... 18 5.2 蒙特卡罗方法简介 ............................................. 18

5.3 蒙特卡罗方法求解体积问题 ..................................... 19 结束语......................................................................................................................................................20 致谢........................................................................................................................................................... 20 参考文献................................................................................................................................................21 附录........................................................................................................................................................... 22

计算物理实践报告学号：姓名：第一章简单物理实验的模拟及数据处理 1.1 问题描述：编写单摆运动演示程序。在不考虑空气阻力和很小的假设下，单位质量小球做理想简谐运动，此时 0  cos    gt L    。 1.2 单摆运动原理单摆是能够产生往复摆动的一种装置，将无重细杆或不可伸长的细柔绳一端悬于重力场内一定点，另一端固结一个重小球，就构成单摆。设在某一时刻，单摆的摆线偏离铅垂线的角位移为，将重力 mg 分解为径向力 F 和切向力 T，则 T 的大小为 sinmg ，切向的加速度 a L  2  2 d dt .根据牛顿第二定律得方程 a L  2  2 d dt   mg sin  从而单摆运动的微分方程为 2 d  2 t    sing L  由于 sin    5 3   3! 5!   当 很小时, sin  所以单摆运动的微分方程可以表示为 2 d  2 t    g L  1.1 由上式可知，当很小时，单摆的角加速度与角位移成正比，方向相反，方  1.2 程的 3 可以表示为 =A cos( )    t ~ 1 ~

计算物理实践报告学号：姓名： 1.3 单摆运动模型如图所示建立物理模型，单摆运动过程中摆线一端固定，另一端小球在平衡位置附近摆动，设小球中心点的坐标为（x,y），由几何关系可知 2 L 2 x  2 y tan        y x 忽略空气阻力且在 很小的情况下，有 0= cos   所以，与式（1.2）比较可得 A= =    ，， 0 =0     gt L     g L x L  sin   L sin y L  cos   L sin        所以，单摆的运动方程为 1.4 MATLAB 仿真    0      0   t         g L g L                 cos cos t 首先，建立坐标轴，根据给出的测试初始值，用 line 函数画出小球的初始位置，然后，根据上面分析的轨迹方程，记录小球在任一时刻的坐标，不断的画图覆盖之前的作坐标图，达到动画的效果，最后，调整 dt 的取值观察何时效果比较明显。在进行仿真的时候取初始值为  0  L , 18  ,1 g  8.9 MATLAB 仿真程序见附录一，程序运行结果如下图。 ~ 2 ~

计算物理实践报告学号：姓名：图 1-1：单摆运动截图 ~ 3 ~

计算物理实践报告学号：姓名：第二章方程组的数值解法 2.1 问题描述二分法求解方程 x3+4x2－10＝0 在区间［1，2］内的根，精度自设。 2.2 二分法简介二分法是一种求解方程根的近似方法，若函数 f(x)在区间[a,b]内单调，且满足 f(a)f(b)<0，则在区间(a,b)内，f(x)=0 有唯一根，取区间[a,b]中点 a b 2 带入函数中并将函数值与 f(a),f(b)比较，如果 f( a b 2 )f(a)<0，则函数的根在 [a, a b 2 ]区间内，反之，则在函数唯一根在[ a b 2 ,b]区间，再次取区间中点计算函数值，缩小根所在的区间，不断重复将区间二分，知道取得满足精度的区间，得到方程的近似根。 2.3 二分法编程原理 1）确定二分法初始区间[a,b]，设定近似解精度 e，迭代次数 n=0 2)计算 f(a),f(b),满足 f(a)f(b)<0 则在区间内必存在一个零点 3）记 x 1  , a x 2  , b x 0  x 1 x 2  2 4）计算 f( 0x )f( 1x ),若 f( 0x )f( 1x )<0，则令 2 x x ，否则，令 1 x 0 x 然 0 后将迭代次数 n 自动加一 ~ 4 ~

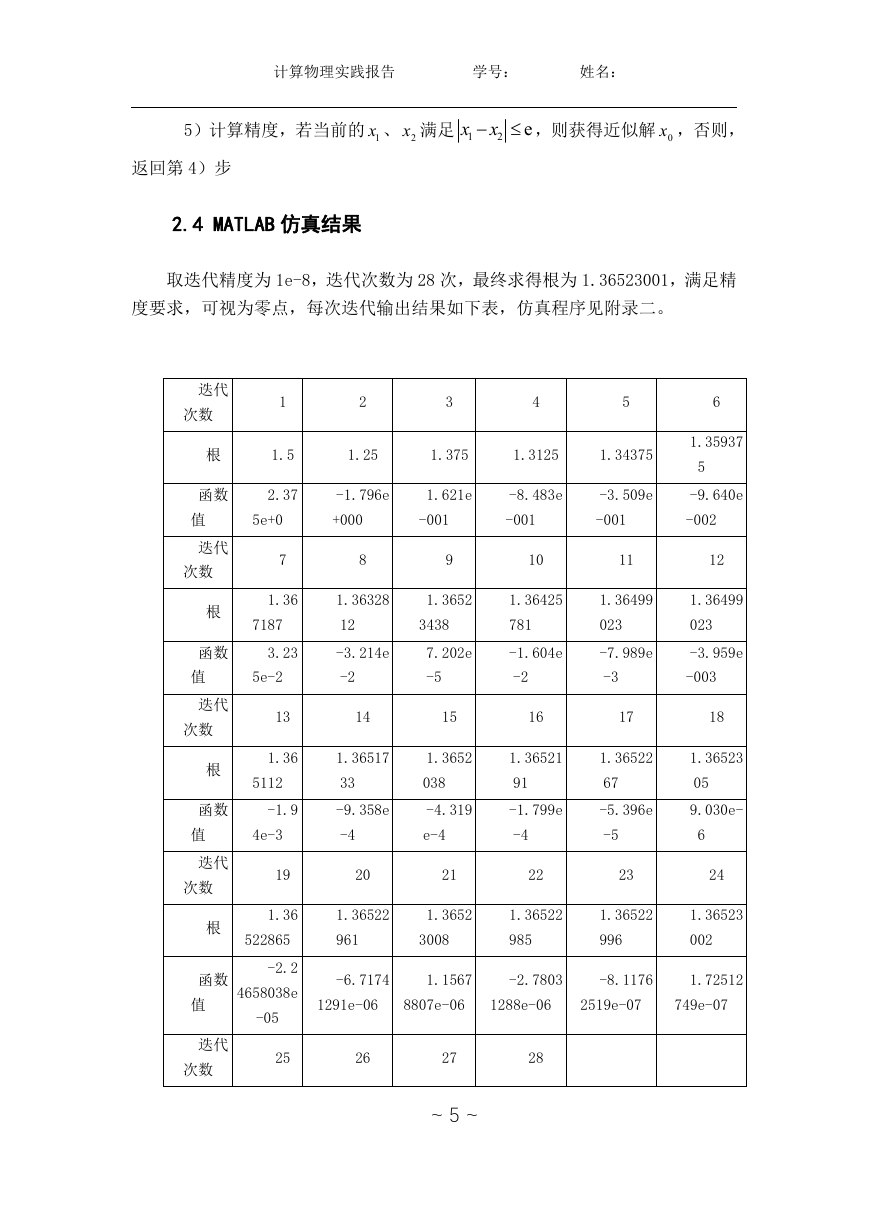
计算物理实践报告学号：姓名： x 5）计算精度，若当前的 1x 、 2x 满足 1 x 2 e  ，则获得近似解 0x ，否则，返回第 4）步 2.4 MATLAB 仿真结果取迭代精度为 1e-8，迭代次数为 28 次，最终求得根为 1.36523001，满足精度要求，可视为零点，每次迭代输出结果如下表，仿真程序见附录二。迭代次数 1 2 3 4 5 6 根 1.5 1.25 1.375 1.3125 1.34375 1.35937 5 函数 2.37 -1.796e 1.621e -8.483e -3.509e -9.640e 值 5e+0 +000 -001 -001 -001 -002 迭代次数根 7 8 9 10 11 12 1.36 1.36328 1.3652 1.36425 1.36499 1.36499 7187 12 3438 781 023 023 函数 3.23 -3.214e 7.202e -1.604e -7.989e -3.959e 值 5e-2 -2 -5 -2 -3 -003 迭代次数根 13 14 15 16 17 18 1.36 1.36517 1.3652 1.36521 1.36522 1.36523 5112 33 038 91 67 05 函数 -1.9 -9.358e -4.319 -1.799e -5.396e 9.030e- 值 4e-3 -4 e-4 -4 -5 19 20 21 22 23 6 24 迭代次数根函数值迭代次数 1.36 1.36522 1.3652 1.36522 1.36522 1.36523 522865 961 3008 985 996 002 -2.2 4658038e -05 -6.7174 1.1567 -2.7803 -8.1176 1.72512 1291e-06 8807e-06 1288e-06 2519e-07 749e-07 25 26 27 28 ~ 5 ~

资料库

南邮应用物理学计算物理实践报告.docx

相关推荐

课程资源

热门标签

最新资料