2021年江苏省徐州市中考数学真题及答案.doc-资料库

第1页 / 共9页

第2页 / 共9页

第3页 / 共9页

第4页 / 共9页

第5页 / 共9页

第6页 / 共9页

第7页 / 共9页

第8页 / 共9页

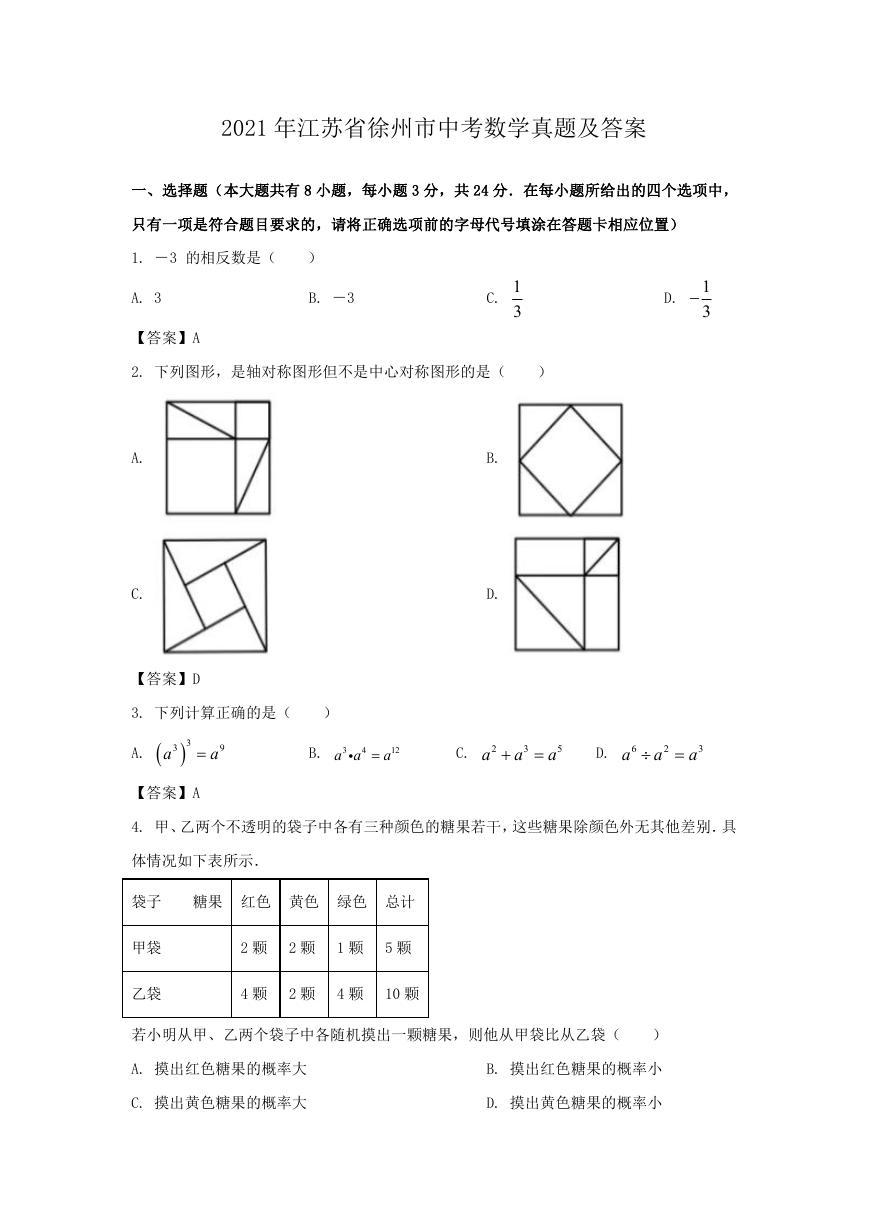
2021 年江苏省徐州市中考数学真题及答案一、选择题（本大题共有 8 小题，每小题 3 分，共 24 分．在每小题所给出的四个选项中，只有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置） 1. －3 的相反数是（） A. 3 B. －3 【答案】A C. 1 3 D.  1 3 2. 下列图形，是轴对称图形但不是中心对称图形的是（） A. C. B. D. 【答案】D 3. 下列计算正确的是（） A.  33 a 9 a 【答案】A B. 4 3 a a  12 a C. 2 a  3 a  5 a D. 6 a  2 a  3 a 4. 甲、乙两个不透明的袋子中各有三种颜色的糖果若干，这些糖果除颜色外无其他差别．具体情况如下表所示．袋子糖果红色黄色绿色总计甲袋乙袋 2 颗 2 颗 1 颗 5 颗 4 颗 2 颗 4 颗 10 颗若小明从甲、乙两个袋子中各随机摸出一颗糖果，则他从甲袋比从乙袋（） A. 摸出红色糖果的概率大 B. 摸出红色糖果的概率小 C. 摸出黄色糖果的概率大 D. 摸出黄色糖果的概率小

【答案】C 5. 第七次全国人民普查的部分结果如图所示．根据该统计图，下列判断错误的是（） A. 徐州 0－14 岁人口比重高于全国 B. 徐州 15－59 岁人口比重低于江苏 C. 徐州 60 岁以上人口比重高于全国 D. 徐州 60 岁以上人口比重高于江苏【答案】D 6. 下列无理数，与 3 最接近的是（） A. 6 【答案】C B. 7 C. 10 D. 11 7. 在平面直角坐标系中，将二次函数 y 2 x= 的图像向左平移 2 个单位长度，再向上平移 1 个单位长度，所得抛物线对应的函数表达式为（） A. y  x  22  1 B. y  x  22  1 C. y  x  22  1 D. y  x  22  1 【答案】B 8. 如图，一枚圆形古钱币的中间是一个正方形孔，已知圆的直径与正方形的对角线之比为 3：1，则圆的面积约为正方形面积的（）

A. 27 倍【答案】C B. 14 倍 C. 9 倍 D. 3 倍二、填空题（本大题共有 10 小题，每小题 3 分，共 30 分．不需写出解答过程，请将答案直接填写在相应位置上） 9. 我市 2020 年常住人口约 9080000 人，该人口数用科学记数法可表示为________人．【答案】9.08×106 10. 49 的平方根是_____. 【答案】±7 11. 因式分解：x2－36= _________．【答案】（x＋6）（x－6） 12. 为使 1x  有意义，则 x 的取值范围是_________．【答案】x≥1 13. 若 1 2 ,x x 是方程 2 3 x x x  的两个根，则 1 0 x 2  _________．【答案】-3 14. 如图， AB 是 O 的直径，点C D、在 O 上，若 BAC  _________°． ADC  58  ，则【答案】32

15. 如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若母线长l 为8cm ，扇形的圆心角 90  ，则圆锥的底面圆半径 r 为__________ cm ．【答案】2 16. 如图，在 ABC 中，点 ,D E 分别在边 ,BA BC 上，且 AD CE DB EB  形 ADEC 的面积的比为__________．  ， DBE  3 2 与四边【答案】 4 21 17. 如图，点 ,A D 分别在函数 y  3  x , y  的图像上，点 ,B C 在 x 轴上．若四边形 ABCD 6 x 为正方形，点 D 在第一象限，则 D 的坐标是_____________．【答案】（2，3） 18. 如图，四边形 ABCD 与 AEGF 均为矩形，点 ,E F 分别在线段 ,AB AD 上．若  2cm BE FD ___________cm ．，矩形 AEGF 的周长为 20cm ，则图中阴影部分的面积为

【答案】16 三、解答题（本大题共有 10 小题，共 86 分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤） 19. 计算：（1） 2   0 2021 3  8 1     1 2    1 a  1 2  1        2 a a （2）  a 1a  a 20. （1）解方程： 2 4 x 【答案】（1）1；（2） x   5 0 （2）解不等式组： 2 1 3 x       2 3 x x   8 【答案】（1） 1 x   ， 2 1 x  ；（2） 5 x   3  ， 21. 如图， AB 为 O 的直径，点C D，在 O 上， AC 与OD 交于点 E ， AE EC OE ED （1） AOE CDE （2）四边形OBCD 是菱形．，连接 BC CD，．求证：    ；

【答案】略 22. 如图，将一张长方形纸片 ABCD 沿 E 折叠，使 ,C A 两点重合．点 D 落在点G 处．已 8 BC  ． AB ，知 =4 （1）求证： AEF （2）求线段 FD 的长．  是等腰三角形；【答案】（1）略；（2）3 23. 某网店开展促销活动，其商品一律按 8 折销售，促销期间用 400 元在该网店购得某商品的数量较打折前多出 2 件．问：该商品打折前每件多少元？【答案】50 24. 如图，是一个竖直放置的钉板，其中，黑色圆面表示钉板上的钉子， 1 A B B 2 , , , D D 4 , 1 , 3 分别表示相邻两颗钉子之间的空隙，这些空隙大小均相等，从入口 1A 处投放一个直径略小于两颗钉子之间空隙的圆球，圆球下落过程中，总是碰到空隙正下方的钉子，且沿该钉子左右两个相邻空隙继续下落的机会相等，直至圆球落入下面的某个槽内．用画树状图的方法，求圆球落入③号槽内的概率．【答案】 3 8 25. 某市近年参加初中学业水平考试的人数（以下简称“中考人数”）的情况如图所示．

根据图中信息，解决下列问题：（1）这 11 年间，该市中考人数的中位数是______________万人；（2）与上年相比，该市中考人数增加最多的年份是____________年；（3）下列选项中，与该市 2022 年中考人数最有可能接近的是（） A. 12.8 万人； B. 14.0 万人；C. 15.3 万人（4）2019 年上半年，该市七、八、九三个年级的学生总数约为（） A. 23.1 万人；B. 28.1 万人；C. 34.4 万人（5）该市 2019 年上半年七、八、九三个年级的数学教师共有 4000 人，若保持数学教师与学生的人数之比不变，根据（3）（4）的结论，该市 2020 年上半年七、八、九三个年级的数学教师较上年同期增加多少人（结果取整数）？【答案】（1）7.6；（2）2020；（3）C；（4）C；（5）721 26. 如图，点 ,A B 在函数 21 x 4 y 轴交于点C ，连接 ,OA OB ． y 的图像上．已知 ,A B 的横坐标分别为－2、4，直线 AB 与（1）求直线 AB 的函数表达式；（2）求 AOB  的面积；（3）若函数 y 21 x 4 的图像上存在点 P ，使得 PAB 的面积等于 AOB  的面积的一半，则这样的点 P 共有___________个．

【答案】（1）直线 AB的解析式为： y x 27. 如图，斜坡 AB 的坡角光伏板的一端位于点 A ，过其另一端 D 安装支架 DE ，DE 所在的直线垂直于水平线 AC ， BAC 13  2  ；（2）6；（3）4 1 2  ，计划在该坡面上安装两排平行的光伏板．前排垂足为点 ,F E 为 DF 与 AB 的交点．已知 AD  100cm ，前排光伏板的坡角 DAC  28  ．（1）求 AE 的长（结果取整数）；（2）冬至日正午，经过点 D 的太阳光线与 AC 所成的角 H 在 AB 上．此时，若要后排光伏板的采光不受前排光伏板的影响，则 EH 的最小值为多  ．后排光伏板的前端 DGA 32  少（结果取整数）？参考数据： 2 1.41, 3 1.73, 6    2.45 三角函数锐角 A 13° 28° 32° sin A cos A tan A 0.22 0.47 0.53 0.97 0.88 0.85 0.23 0.53 0.62 【答案】（1）91cm ；（2） 32cm 28. 如图 1，正方形 ABCD 的边长为 4，点 P 在边 AD 上（ P 不与 ,A D 重合），连接 ,PB PC ．将线段 PB 绕点 P 顺时针旋转 90°得到 PE ，将线段 PC 绕点 P 逆时针旋转 90°

资料库

2021年江苏省徐州市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料