THE WAVELET TUTORIAL 翻译.docx-资料库

shuting111-10908632-4744300845367830667.docx.pdf-第1页.png

第1页 / 共68页

shuting111-10908632-4744300845367830667.docx.pdf-第2页.png

第2页 / 共68页

shuting111-10908632-4744300845367830667.docx.pdf-第3页.png

第3页 / 共68页

shuting111-10908632-4744300845367830667.docx.pdf-第4页.png

第4页 / 共68页

shuting111-10908632-4744300845367830667.docx.pdf-第5页.png

第5页 / 共68页

shuting111-10908632-4744300845367830667.docx.pdf-第6页.png

第6页 / 共68页

shuting111-10908632-4744300845367830667.docx.pdf-第7页.png

第7页 / 共68页

shuting111-10908632-4744300845367830667.docx.pdf-第8页.png

第8页 / 共68页

小波变换教程一、序言欢迎来到这个小波变换的入门教程。小波变换是一个相对较新的概念（大概十年的样子），但是有关于它的文章和书籍却不少。这其中大部分都是由搞数学的人写给其他搞数学的人看的，不过，仍然有大部分搞数学的家伙不知道其他同行们讨论的是什么（我的一个数学教授就承认过）。换言之，大多数介绍小波变换的文献对那些小波新手们来说用处不大（仅仅为个人观点）。当我刚开始学习小波变换的时候，曾经为了弄明白这个神奇的领域到底说的是什么困扰了好多天，因为在这个领域的入门书籍少之又少。为此我决定为那些小波新手们写这个入门级的教程。我自己当然也是一个新手，也有很多理论性的细节没有弄清楚。不过，考虑到其工程应用性，我觉得没有必要弄清楚所有的理论细节。在这篇教程中，我将试图给出一些小波理论的基本原理。我不会给出这些原理和相关公式的证明，因为我假定预期的读者在读这个教程时并不需要知道这些。不过，感兴趣的读者可以直接去索引（所列的书籍）中获取更为深入的信息。在这篇文档中，我假定你没有任何相关知识背景。如果你有，请忽略以下的信息，因为都是一些很琐碎的东西。如果你发现教程中有任何不一致或错误的信息，请联系我。我将乐于看到关于教程的任何评论。二、变换什么首先，我们为什么需要（对信号做）变换，到底什么是变换？原始信号中有一些信息是很难获取的，为了获得更多的信息，我们就需要对原始信号进行数学变换。在接下来的教程中，我将时域内的信号视为原始信号，经过数学变换后的信号视为处理信号。可用的变换有很多种，其中傅立叶变换可能是最受欢迎的一种。 1 / 68

实际中很多原始信号都是时域内的信号，也就是说不管信号是如何测得的，它总是一个以时间为变量的函数。换言之，当我们画信号图的时候，横轴代表时间（独立变量），纵轴代表信号幅度（非独立变量）。当我们画信号的时域图时，我们得到了信号的时幅表示。对大多数信号处理应用来说，这种表示经常不是最好的表示。在很多时候，大量特殊的信息是隐藏在信号的频率分量中的。信号的频谱图表示的一般是信号中的频率分量。频谱图展示了原始信号中存在哪些频率分量。直觉上，我们都知道频率意味着某种事物的变化速率。如果某种东西（用正确的技术术语来说是一个数学或物理变量）变化的很快，我们说它的频率高，如果它变换的不快，我们就说它的频率低。如果这个变量一直保持不变，我们说它的频率为 0，或者说没有频率。举例来说，日报的频率就比月刊高（因为它出版快）。频率用周期/秒，或者用一个更广泛的说法，赫兹来衡量。举例来说，我们日常生活中用的电的频率是 60Hz（世界上的其他国家是 50Hz）。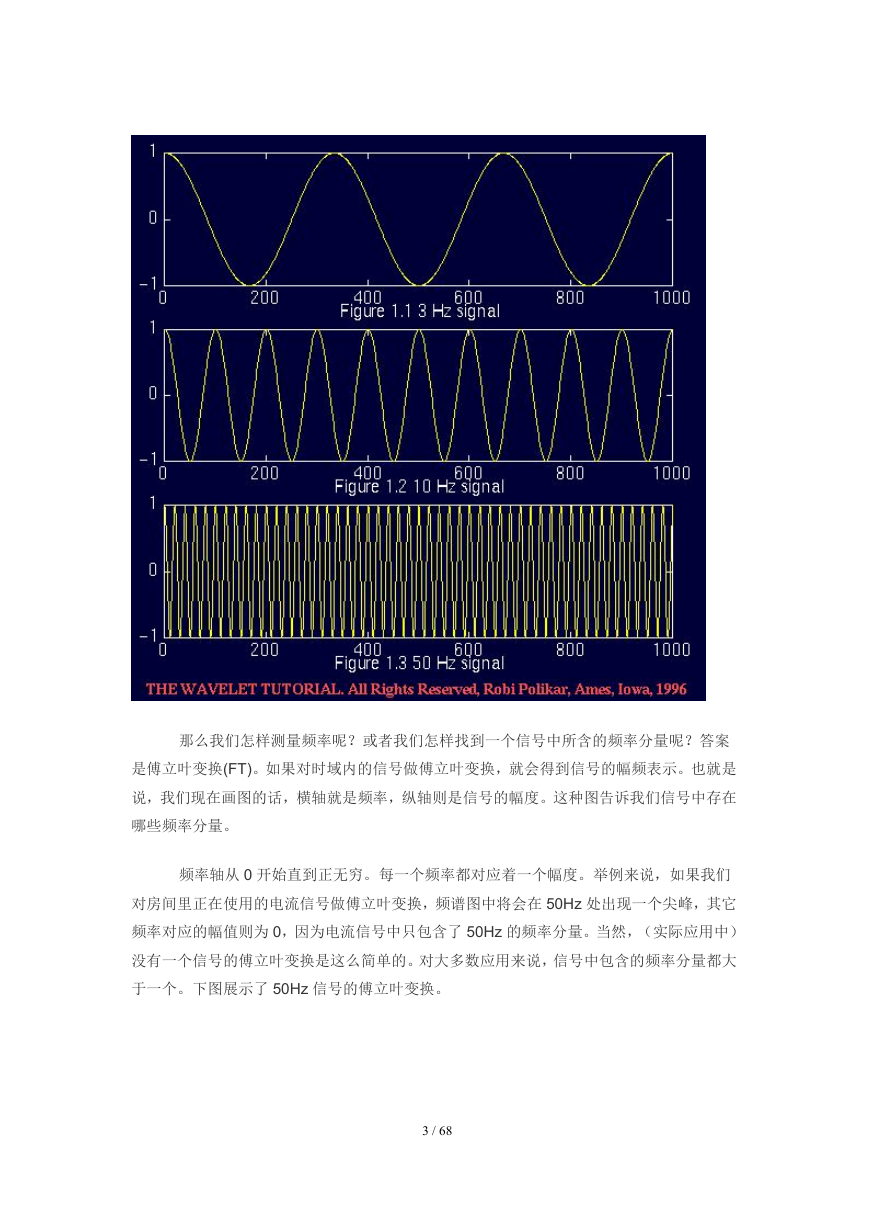这意味着如果我们想要画一条电流曲线的话，我们将会看到的是 1 秒内出现的 50 个重复的正弦波。现在，观看以下这些图。第一幅图中正弦信号的频率是 3Hz，第二幅是 10Hz，第三幅则是 50Hz。 2 / 68

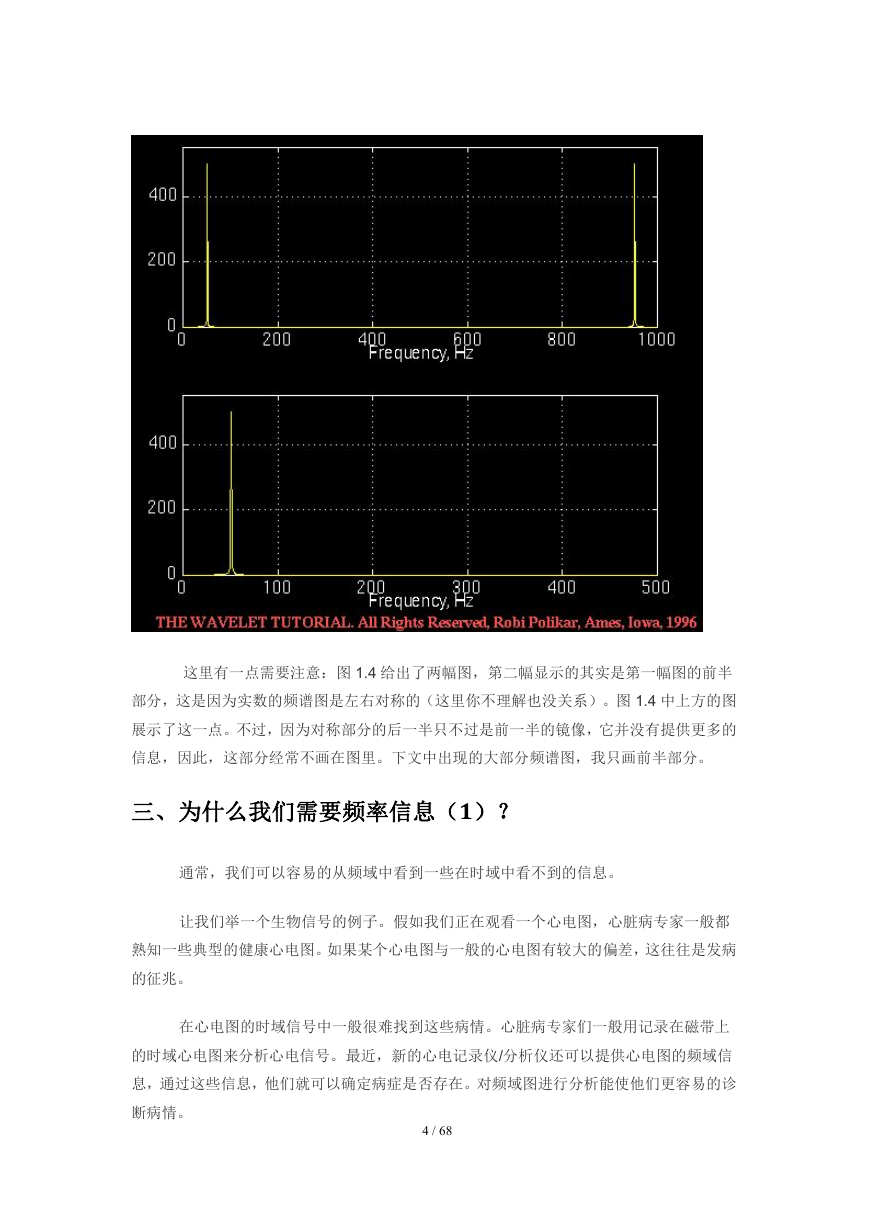
那么我们怎样测量频率呢？或者我们怎样找到一个信号中所含的频率分量呢？答案是傅立叶变换(FT)。如果对时域内的信号做傅立叶变换，就会得到信号的幅频表示。也就是说，我们现在画图的话，横轴就是频率，纵轴则是信号的幅度。这种图告诉我们信号中存在哪些频率分量。频率轴从 0 开始直到正无穷。每一个频率都对应着一个幅度。举例来说，如果我们对房间里正在使用的电流信号做傅立叶变换，频谱图中将会在 50Hz 处出现一个尖峰，其它频率对应的幅值则为 0，因为电流信号中只包含了 50Hz 的频率分量。当然，（实际应用中）没有一个信号的傅立叶变换是这么简单的。对大多数应用来说，信号中包含的频率分量都大于一个。下图展示了 50Hz 信号的傅立叶变换。 3 / 68

这里有一点需要注意：图 1.4 给出了两幅图，第二幅显示的其实是第一幅图的前半部分，这是因为实数的频谱图是左右对称的（这里你不理解也没关系）。图 1.4 中上方的图展示了这一点。不过，因为对称部分的后一半只不过是前一半的镜像，它并没有提供更多的信息，因此，这部分经常不画在图里。下文中出现的大部分频谱图，我只画前半部分。三、为什么我们需要频率信息（1）？通常，我们可以容易的从频域中看到一些在时域中看不到的信息。让我们举一个生物信号的例子。假如我们正在观看一个心电图，心脏病专家一般都熟知一些典型的健康心电图。如果某个心电图与一般的心电图有较大的偏差，这往往是发病的征兆。在心电图的时域信号中一般很难找到这些病情。心脏病专家们一般用记录在磁带上的时域心电图来分析心电信号。最近，新的心电记录仪/分析仪还可以提供心电图的频域信息，通过这些信息，他们就可以确定病症是否存在。对频域图进行分析能使他们更容易的诊断病情。 4 / 68

上面只是一个说明了为何频率幅值有用的简单例子。当前，傅立叶变换已经被用于不同的领域，这些领域包括工程学的各个分支。虽然傅立叶变换是最流行的数学变换，但它并不是唯一的。工程师和数学家们还经常会用到很多其他的变换。如希尔伯特变换、短时傅立叶变换（后文对此有详细阐述）、魏格纳分布和雷登变换，当然还有我们要讲的特征变换——小波变换。这些变换只不过是工程师和数学家们所用到的变换中的一小部分。每一种变换都有自己的应用领域，也都各有优缺点，小波变换也不例外。为了更好的理解小波变换的必要性，让我们更详细的探讨一下傅立叶变换。傅立叶变换是一种可逆变换，即它允许原始信号和变换过的信号之间互相转换。不过，在任意时刻只有一种信息是可用的，也就是说，在傅立叶变换后的频域中不包含时间信息，逆变换后的时域中不包含时间信息。说到这里，脑袋里很自然的就会提出这个问题，有没有一种变换可以同时提供时间和频率信息呢？我们马上就会知道，答案是具体问题具体分析。回想一下，傅立叶变换给出了信号中包含的频率信息，即它可以告诉我们原始信号中不同频率的信号到底有多少，但是并没有告诉我们某个频率信号是在何时出现的。在处理平稳信号时，我们不需要知道这些。让我们进一步探讨一下平稳这个概念，因为它在信号分析中具有重要意义。如果某个信号中的频率分量一直保持不变，则我们叫这类信号为平稳信号。换句话说，静态信号中的频率分量一直保持不变。这种情况下，就不需要知道频率分量是什么时候出现的，因为所有的频率分量出现在信号的每一刻！！！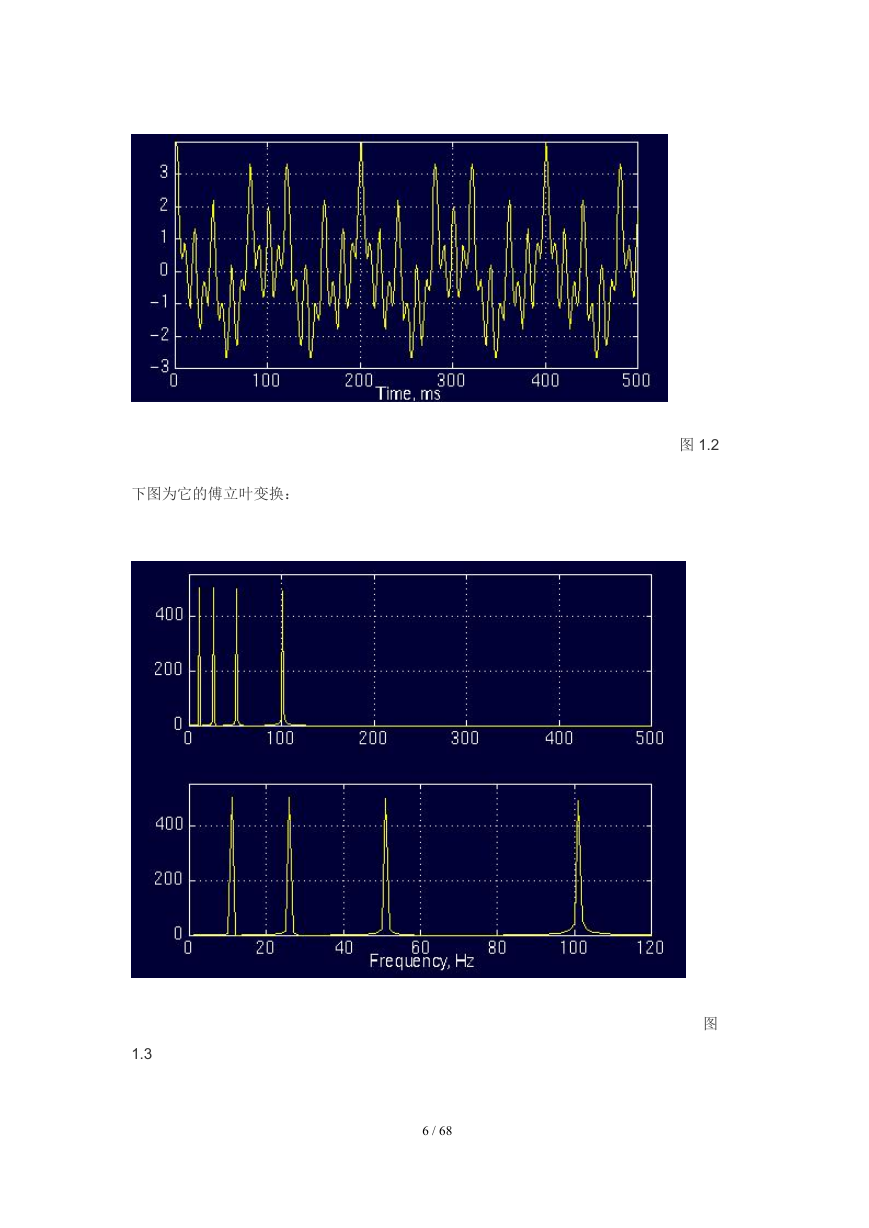以下面这个信号为例： x(t)=cos(2*pi*10*t)+cos(2*pi*25*t)+cos(2*pi*50*t)+cos(2*pi*100*t) 这是一个平稳信号，因为频率为 10，25，50 和 100Hz 的频率分量出现在整个时域内。如下图所示： 5 / 68

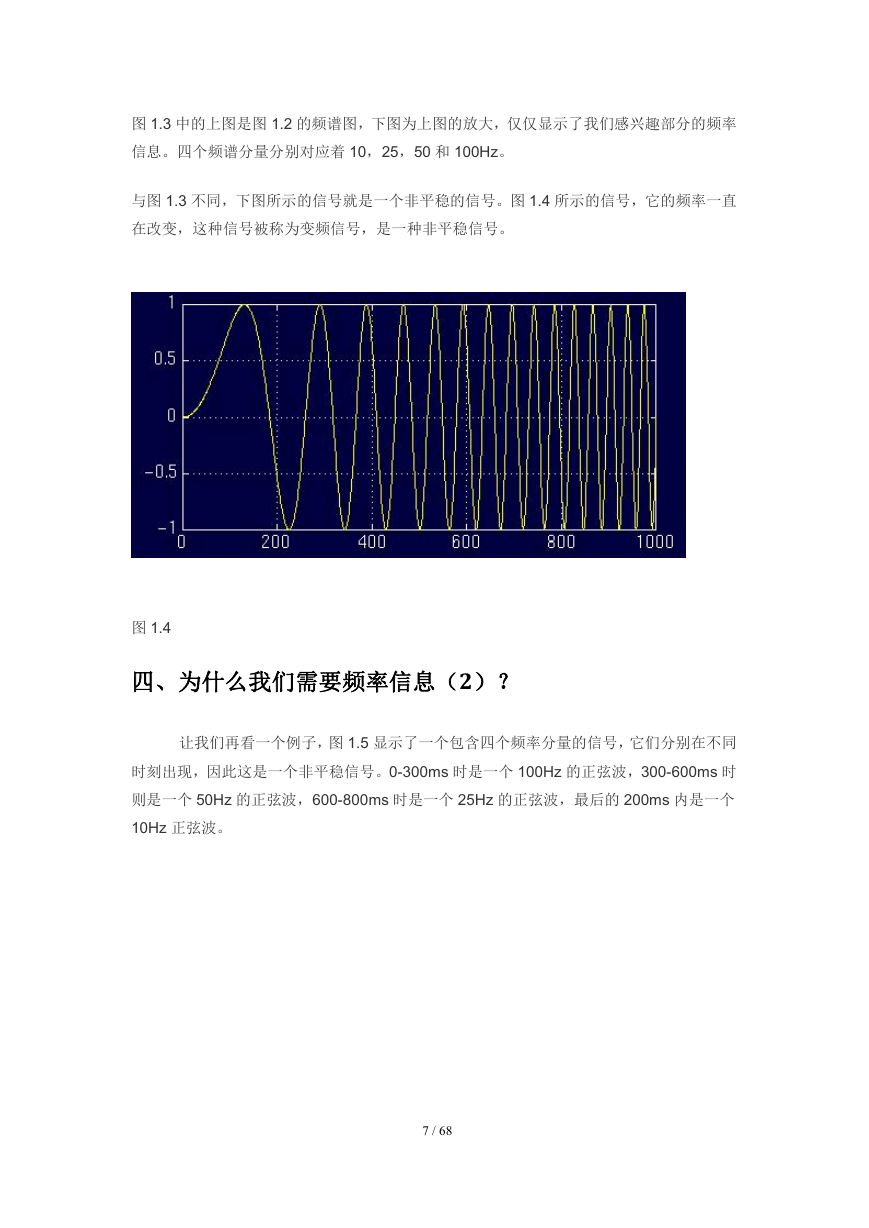
下图为它的傅立叶变换： 1.3 6 / 68 图 1.2 图

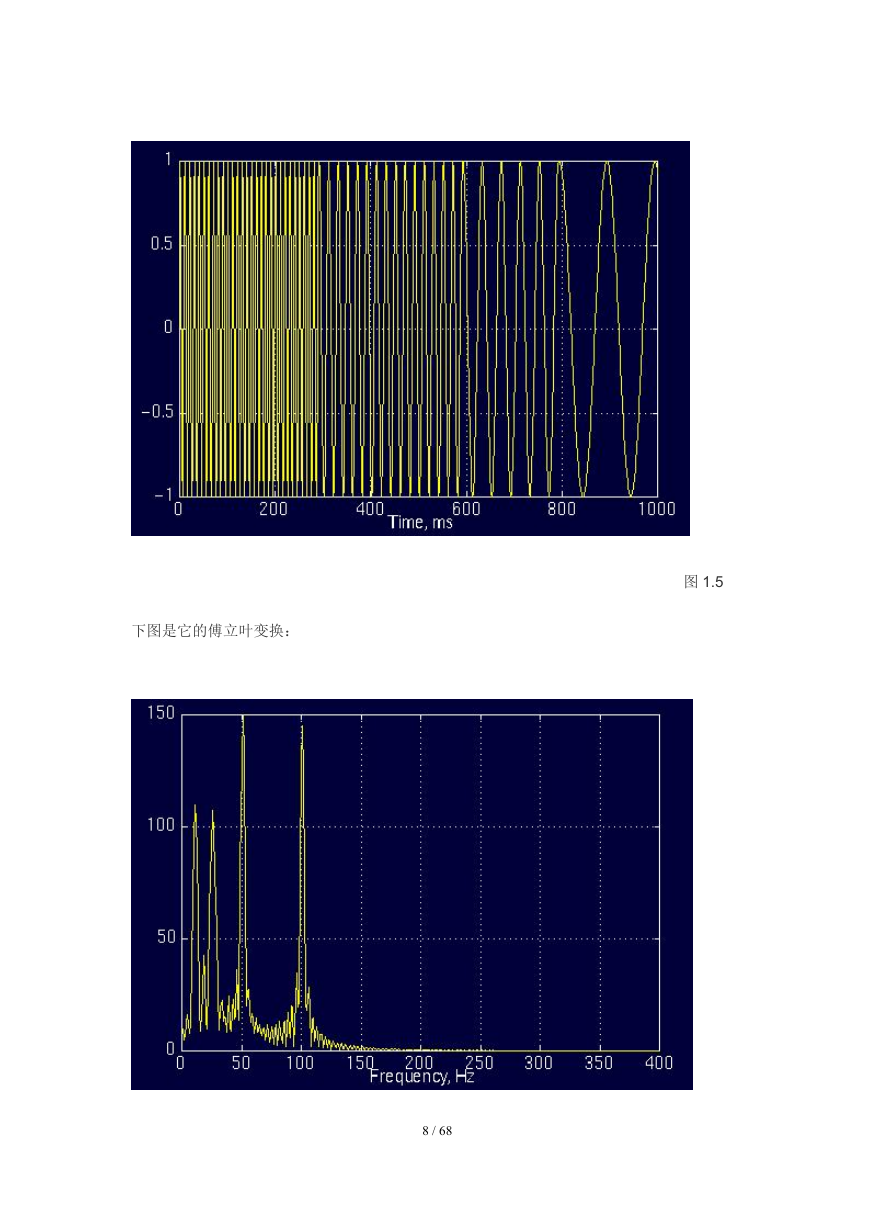
图 1.3 中的上图是图 1.2 的频谱图，下图为上图的放大，仅仅显示了我们感兴趣部分的频率信息。四个频谱分量分别对应着 10，25，50 和 100Hz。与图 1.3 不同，下图所示的信号就是一个非平稳的信号。图 1.4 所示的信号，它的频率一直在改变，这种信号被称为变频信号，是一种非平稳信号。图 1.4 四、为什么我们需要频率信息（2）？让我们再看一个例子，图 1.5 显示了一个包含四个频率分量的信号，它们分别在不同时刻出现，因此这是一个非平稳信号。0-300ms 时是一个 100Hz 的正弦波，300-600ms 时则是一个 50Hz 的正弦波，600-800ms 时是一个 25Hz 的正弦波，最后的 200ms 内是一个 10Hz 正弦波。 7 / 68

下图是它的傅立叶变换：图 1.5 8 / 68

资料库

THE WAVELET TUTORIAL 翻译.docx

相关推荐

音视频

热门标签

最新资料