基于傅里叶变换和鬼成像算法的多图像加密方案研究.pdf-资料库

Current Optics and Photonics Vol. 2, No. 4, August 2018, pp. 315-323 ISSN: 2508-7266(Print) / ISSN: 2508-7274(Online) DOI: https://doi.org/10.3807/COPP.2018.2.4.315 Research on Multiple-image Encryption Scheme Based on Fourier Transform and Ghost Imaging Algorithm Zhang Leihong1, Yuan Xiao1 *, Zhang Dawei1, and Chen Jian2 1University of Shanghai for Science and Technology, Shanghai 200093, China 2Anhui Province Key Laboratory of Nondestructive Evaluation, Hefei 230031,China (Received April 26, 2018 : revised July 4, 2018 : accepted July 11, 2018) A new multiple-image encryption scheme that is based on a compressive ghost imaging concept along with a Fourier transform sampling principle has been proposed. This further improves the security of the scheme. The scheme adopts a Fourier transform to sample the original multiple-image information respectively, utilizing the centrosymmetric conjugation property of the spatial spectrum of the images to obtain each Fourier coefficient in the most abundant spatial frequency band. Based on this sampling principle, the multiple images to be encrypted are grouped into a combined image, and then the compressive ghost imaging algorithm is used to improve the security, which reduces the amount of information transmission and improves the information transmission rate. Due to the presence of the compressive sensing algorithm, the scheme improves the accuracy of image reconstruction. Keywords : Fourier transform, Compressive sensing, Ghost imaging, Multiple-image Encryption OCIS codes : (070.2575) Fractional Fourier transforms; (100.3010) Image reconstruction techniques; (200.4560) Optical data processing I. INTRODUCTION information With the rapid development of computer and Internet technologies, information security has attracted more and more researchers. Due to the ultra-high speed and multiple dimensional processing, optical security technology has been popular for a long time, including double random phase encryption technology [1-5] and ghost imaging technology [6-10]. As another important branch of optical encryption, multiple-image encryption technology has attracted more and more attention because it not only improves the encryption ability but also reduces the data volume of the ciphertext. As far as multi-image encryption technology is concerned, it mainly focuses on researching new methods for simultaneous encryption of multiple images, to enhance the security of data and improve the robustness of the system. Klyshko proposed a ghost imaging scheme that has attracted more and more attention owing to its remarkable physical properties [6]. Katz et al. achieved computational ghost imaging based on a compressive sensing algorithm instead of the intensity correlation operation, which greatly reduces the number of measurements; when the signals and images are sparse or can be sparse in some transform domains, the use of a compressive sensing algorithm can directly measure and simultaneously compress the signal or image. Finally, the signal will be reconstructed by the receiver’s reconstruction algorithm [11-13]. In order to improve coding efficiency, the methods of multiple-image encryption based on position multiplexing and computational ghost imaging [14]; double random phase encryption [15] etc. have been proposed. Lee and Cho [15] proposed a multiple-image transmission method based on double random phase encryption using orthogonal encoding, which uses two random phase masks and orthogonal encoding. The orthogonal encoding for multiple images uses a larger Hadamard matrix than that for a single image, increasing the security of encryption. Li et al. [16] proposed *Corresponding author: yxhello365@163.com, ORCID 0000-0002-2878-3217. Color versions of one or more of the figures in this paper are available online. * This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/ licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited. *Copyright 2018 Current Optics and Photonics - 315 -

316 Current Optics and Photonics, Vol. 2, No. 4, August 2018 a multiple-image encryption method based on compressive ghost imaging, in which an improved logistic mapping algorithm and the coordination of sampling were used to achieve multiple-image encryption and decryption; Wu et al. [17] proposed a multiple-image encryption scheme based on computational ghost imaging with different diffraction distances, each plane image is encrypted into an intensity vector, and then all the intensity vectors are added together to generate the final density in order to improve the effectiveness and security of the multiple-image encryption scheme; Yuan et al. [18] proposed a multi-image encryption scheme with a single-pixel detector according to the principle of ghost imaging. In this scheme, all the emitted light is recorded by a single-pixel barrel detector to obtain ciphertext, and any secret images can be independently decrypted from the ciphertext. The above encryption methods are provided with good security, but in computational ghost imaging, thousands of calculations are needed to obtain acceptable results. In some applications, a large amount of storage space is required for optical image encryption based on ghost imaging. In this sense, we propose a multi-image encryption scheme based on Fourier transforms and compressive ghost imaging. The images adopt Fourier transforms to obtain the image information. According to different sampling rates, multiple images are synthesized into an image in the Fourier space. Then the encryption and decryption was achived by the compressive ghost imaging algorithm, which realizes data compression and reduces the storage space of the data. Firstly, the theoretical analysis and description of the method are given, and then simulation verification is carried out. Finally, the conclusion is drawn. II. THEORETICAL ANALYSIS 2.1. Optical Encryption Mechanism Based on Compressive Ghost Imaging Algorithm In the computational ghost imaging encryption system, the spatial light modulator (SLM) that inputs a series of phase masks is used, as shown in Fig. 1 [19]. The plane wave is modulated by the phase masks and a Fresnel diffraction occurrs with a distance Z from phase masks plane to object plane. Then the light intensity distribution in the object plane could be calculated by using the Fresnel diffraction, which can be expressed as [20] yxI ,( i ) = FrTz { exp[ j 2 πϕ i ,( yx } 2 )] (1) { } FrT ,( where ) yxϕ represents the Fresnel diffraction transform, is the pixel distribution of each phase mask, whose pixel values are randomly from 0 to 1. The subscript “i” represents the i-th measurement value using the i-th phase mask, and the subscript “Z” represents diffraction distance, and the amplitude of the plane wave is defined as unit one. FIG. 1. Schematic of computional ghost image encryption system. Therefore, the new imaging process only requires a bucket B , which can be detector (BD) to obtain the ciphertext expressed as i B i ,(∫= yxIyxT ,( ) i ) dxdy (2) yxT ,( ) where the is the image to be encrypted. Therefore, the image T to be encrypted is successfully encoded in a series of light intensity ciphertext data B using the phase mask key and the distance parameter Z. During the decryption process, an intensity-related operation occurred between the intensity distribution and intensity ciphertext data B from the bucket detector to calculate a secret image, which can be expressed as ,( yxI ) i i yxG ,( ) 〈= yxIB ,( ) 〈−〉 yxIB ,( 〉〈 i i i i ) 〉 (3) where 〈•〉 represents the average operation. However, the ghost imaging algorithm is a statistical feature extraction process. The detection time required for imaging and the resolution time for the reconstruction algorithm are relatively long. In order to solve this problem, Donoho proposed a new reconstruction algorithm based on compressive sensing, which greatly reduced the number of exposure samplings and reduced the amount of computation. At the same time, more encrypted information can be transmitted and the amount of information transmitted is increased under the same calculation conditions. That is to say, the ghost imaging combined with the compressive sensing algorithm successfully solves the problems of long imaging time and low accuracy of object reconstruction. The specific encryption process is: the plaintext image   to be encrypted is a two-dimensional image, and the size is  ×  which is stretched into a column vector ( × ). For the m-th measurement, the light distribution ） function of the reference arm at the pixel point is , whose matrix , expression is: 2,1= 2,1 , = qp （ x , m , N y x n ) ( y I p q p q , m = I m ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ I m 11 I m 21 I m 1 n I m 2 n I m 1 n I m nn ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ (4)

Research on Multiple-image Encryption Scheme Based on … - Zhang Leihong et al. 317 The matrix size is  × ,   is the intensity of the light measured by the m-th measurement at the pixel point () of the CCD measurement plane, which is stretched into a one-dimensional row vector. After N times of measurement, the N  ×  one-dimensional row vectors recorded by the CCD are stored in columns to get a  , the size of which is  ×  and as random matrix  a measurement matrix  of compressive sensing, ie The matrix of the sampling image is represented in Eq. (9), where (x,y) denotes a two-dimensional matrix in the spatial domain and (u,v) denotes a two-dimensional matrix in the Fourier domain. The value of i varies from 1 to k, where k is the total number of images to be encrypted, the images are sampled by a sampling operation to obtain useful information in the images; ),( vus i Ω= i ),( yxfFvu ,( [ i ]) (9)        ⋯        ⋯         The expression of the encryption process is:       ⋮          ⋯   ⋯    ⋯   ⋯   ⋮ ⋱ ⋮ ⋱ ⋮  ⋯   ⋯             ⋮  ⋮  (5) (6)  (a) (b) (c) (d) A compressive sensing algorithm is used for decryption. The original signal can be reconstructed from these projections with high probability by solving an optimization problem. The minimum  norm convex programming problem is shown in Eq. (7). The CS reconstruction algorithm recovers the signal as in Eq. (8). min∥∥ st        ′argmin∥ ′  ∥ (7) (8) 2.2. Fourier Transform Encryption/ Sampling Principle The two-dimensional image Fourier transform is to convert the distribution of image luminance values in the spatial domain to the frequency domain distribution of the image. In this paper, the fast Fourier transform (FFT) can be used to convert the image signal from the spatial domain to the frequency domain for analysis. Using the sparseness and conjugacy of the spatial spectrum of the image, the important information of the image is obtained according to different sampling rates in the Fourier space. In this paper, four binary images are taken as an example. The spectrum and sampling are shown in Figs. 2 and 3. 2.3. The Method of Multiple-Image Encryption The multiple-image encryption and decryption process based on the Fourier transform and compressive ghost imaging algorithm are shown in Figs. 4 and 5. The main steps are as follows: (1) Fourier transforms are applied to the multiple images and converted from spatial domain to frequency domain; (2) In the frequency domain, multiple images are sampled and combined to form a single ciphertext, and the formed single ciphertext is used as the plaintext image of the next encryption algorithm with ghost imaging. (e) (f) (g) (h) FIG. 2. (a-d) are four original images; (e-h) are their corres- ponding spectrograms. (a) (b) (c) (d) (e) FIG. 3. (a-e) are spatial spectra with sampling rates of 6%, 11%, 25%, 50%, and 75%. FIG. 4. Multiple-Image encryption schematic based on Fourier transform and Compressive sensing ghost imaging algorithm.

318 Current Optics and Photonics, Vol. 2, No. 4, August 2018 (a) (b) (c) (d) (e) (f) (g) (h) (i) (j) (k) (l) (m) (n) FIG. 6. (a-d) are the original images; (e-h) are the corres- ponding spectrograms; (i) is the combined image with a sampling rate rate of 50%; (j) is the combined ciphertext (The real part and the imaginary part are respectively subjected to ghost imaging and then recombined into a plural form); (k-n) are different reconstruction images. 3.1. Feasibility Analysis the optical information encryption method Feasibility refers to the situation where the recipient recovers the original graphic information by using the key shared by the sender and the ciphertext delivered on the common channel. The feasibility assessment is performed using to reconstruct the resolution of the plaintext information, which is measured using subjective judgments and objective parameters. In this section we will discuss the feasibility of the encryption method, and compare the Fourier transform and compressive ghost imaging (FFT-CGI) with the Fourier transform and ghost imaging algorithm (FFT-GI). As shown in Figs. 7 and 8. In order to objectively and accurately evaluate the quality of the recovered images using the encryption method. The commonly used objective evaluation indicators include mean square error (MSE) and peak signal-to-noise ratio (PSNR). The basic idea is to measure the degree of deviation of the pixels of the reconstructed image from the corresponding pixels of the original image to evaluate the quality of the reconstructed image. For a size of M × N image, the mathematical expression for MSE and PSNR is: FIG. 5. Multiple-image decryption schematic based Fourier transform and compressive ghost imaging algorithm. (3) Since the formed single ciphertext is of the character- istics of a complex-valued function, it is separated into real and imaginary parts. Then, they are transmitted and encrypted by using ghost imaging. With a random modulation signal as the key, encryption can be achieved due to the randomness of the key; (4) The compressive sensing algorithm is used to decrypt separately the transmitted ciphertexts and combine the decrypted parts into a plural form. Therefore, the combined image is obtained. The combined image contains the reconstructed multiple images through ),( vuΩ operation; (5) The inverse Fourier transform is performed on the reconstructed images to obtain the original images. III. SIMULATION RESULTS AND ANALYSIS In order to verify the effectiveness and feasibility of this method, a numerical experiment was carried out for this method. The experiment was mainly realized by MATLAB software. The selected experimental object is four 64 × 64 binary images. The four binary images adopt are transformed, and the transformed images are sampled according to different sampling rates; the images obtained by Fourier transform sampling are used as the plaintext images of the compressive ghost imaging algorithm. That is, the object   to be imaged; Transforming a pre-fabricated light   into a row as a measurement field intensity matrix  matrix  for the compressive ghost imaging algorithm; The measured value obtained by multiplying the pre-determined light field intensity matrix and the binary image is taken as the total light intensity , and the N precast light field intensity matrices are arranged in order to form a measurement matrix . The object to be imaged is measured to obtain N measurement values, and the image of the object is reconstructed by Eq. (5). The simulation results are shown in Fig. 6.

Research on Multiple-image Encryption Scheme Based on … - Zhang Leihong et al. 319      ′             ×      lg  max  (10) (11) where   an  ′   represent respectively the pixel value of the original image and the restored image, max represents the value of the largest pixel in the image. The larger the PSNR value, the more similar the two images are. That is, the higher the recovered picture quality, the better the encryption algorithm is. FIG. 7. Reconstruction images of FFT-CGI (a1-d1) are the original images; (e1-h1) are the reconstructed images with the sampling rate of 6%; (i1-l1) are the reconstructed images with the sampling rate of 11%; (m1-p1) are the reconstructed images with the sampling rate of 25%; (q1-t1) are the reconstructed images with the sampling rate of 50%; (u1-x1) are the reconstructed images with the sampling rate of 70%. FIG. 8. Reconstruction images of FFT-GI (a2-d2) are the original images; (e2-h2) are the reconstructed images with the sampling rate of 6%; (i2-l2) are the reconstructed images with the sampling rate of 11%; (m2-p2) are the reconstructed images with the sampling rate of 25%; (q2-t2) are the reconstructed images with the sampling rate of 50%; (u2-x2) are the reconstructed images with the sampling rate of 70%.

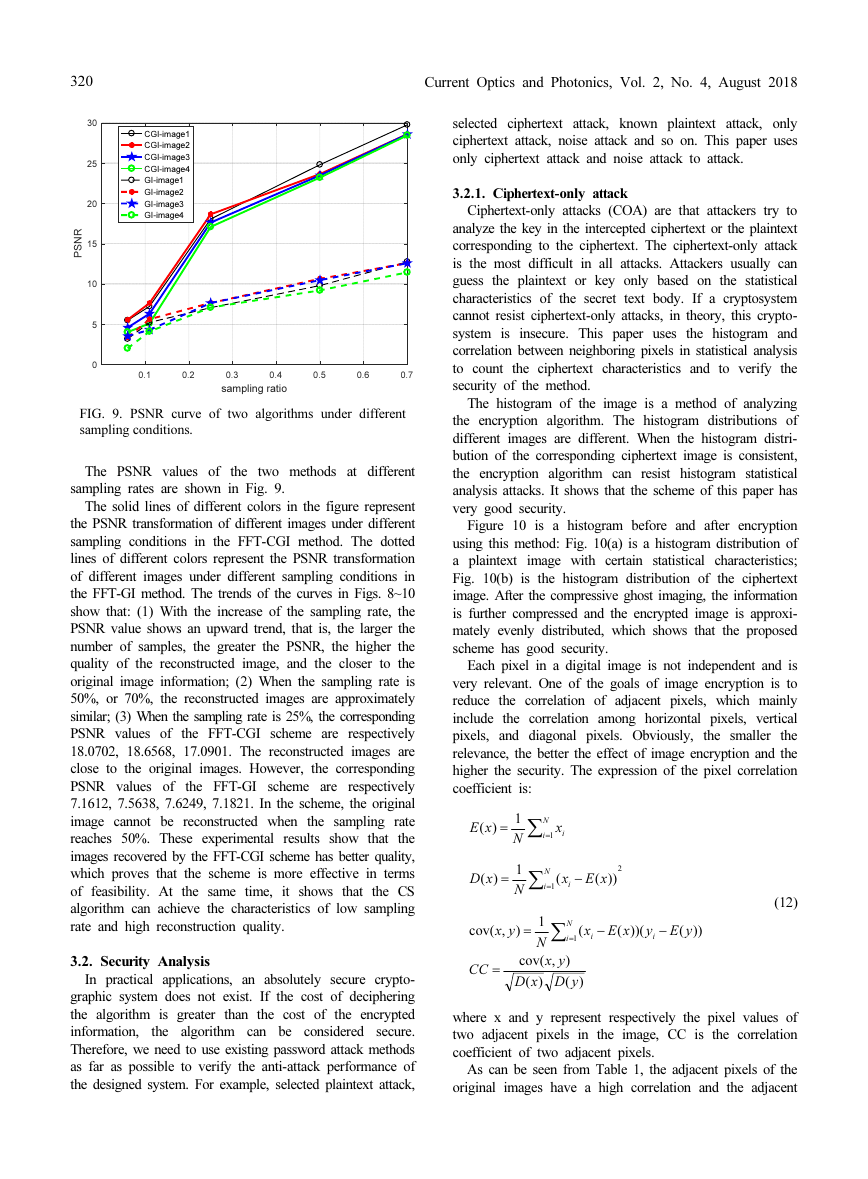
CGI-image1 CGI-image2 CGI-image3 CGI-image4 GI-image1 GI-image2 GI-image3 GI-image4 320 R N S P 30 25 20 15 10 5 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 sampling ratio FIG. 9. PSNR curve of two algorithms under different sampling conditions. The PSNR values of the two methods at different sampling rates are shown in Fig. 9. The solid lines of different colors in the figure represent the PSNR transformation of different images under different sampling conditions in the FFT-CGI method. The dotted lines of different colors represent the PSNR transformation of different images under different sampling conditions in the FFT-GI method. The trends of the curves in Figs. 8~10 show that: (1) With the increase of the sampling rate, the PSNR value shows an upward trend, that is, the larger the number of samples, the greater the PSNR, the higher the quality of the reconstructed image, and the closer to the original image information; (2) When the sampling rate is 50%, or 70%, the reconstructed images are approximately similar; (3) When the sampling rate is 25%, the corresponding PSNR values of the FFT-CGI scheme are respectively 18.0702, 18.6568, 17.0901. The reconstructed images are close to the original images. However, the corresponding PSNR values of the FFT-GI scheme are respectively 7.1612, 7.5638, 7.6249, 7.1821. In the scheme, the original image cannot be reconstructed when the sampling rate reaches 50%. These experimental results show that the images recovered by the FFT-CGI scheme has better quality, which proves that the scheme is more effective in terms of feasibility. At the same time, it shows that the CS algorithm can achieve the characteristics of low sampling rate and high reconstruction quality. 3.2. Security Analysis In practical applications, an absolutely secure crypto- graphic system does not exist. If the cost of deciphering the algorithm is greater than the cost of the encrypted information, the algorithm can be considered secure. Therefore, we need to use existing password attack methods as far as possible to verify the anti-attack performance of the designed system. For example, selected plaintext attack, Current Optics and Photonics, Vol. 2, No. 4, August 2018 selected ciphertext attack, known plaintext attack, only ciphertext attack, noise attack and so on. This paper uses only ciphertext attack and noise attack to attack. 3.2.1. Ciphertext-only attack Ciphertext-only attacks (COA) are that attackers try to analyze the key in the intercepted ciphertext or the plaintext corresponding to the ciphertext. The ciphertext-only attack is the most difficult in all attacks. Attackers usually can guess the plaintext or key only based on the statistical characteristics of the secret text body. If a cryptosystem cannot resist ciphertext-only attacks, in theory, this crypto- system is insecure. This paper uses the histogram and correlation between neighboring pixels in statistical analysis to count the ciphertext characteristics and to verify the security of the method. The histogram of the image is a method of analyzing the encryption algorithm. The histogram distributions of different images are different. When the histogram distri- bution of the corresponding ciphertext image is consistent, the encryption algorithm can resist histogram statistical analysis attacks. It shows that the scheme of this paper has very good security. Figure 10 is a histogram before and after encryption using this method: Fig. 10(a) is a histogram distribution of a plaintext image with certain statistical characteristics; Fig. 10(b) is the histogram distribution of the ciphertext image. After the compressive ghost imaging, the information is further compressed and the encrypted image is approxi- mately evenly distributed, which shows that the proposed scheme has good security. Each pixel in a digital image is not independent and is very relevant. One of the goals of image encryption is to reduce the correlation of adjacent pixels, which mainly include the correlation among horizontal pixels, vertical pixels, and diagonal pixels. Obviously, the smaller the relevance, the better the effect of image encryption and the higher the security. The expression of the pixel correlation coefficient is: )( xE = )( xD = 1 N 1 N ∑ N i 1 = x i ∑ N i 1 = ( xEx ( − i 2 )) 1 ∑ N i 1 = ( xEx ( − i ()) yEy ( − i )) (12) cov( , yx ) = N cov( , yx ) CC = )( yDxD )( where x and y represent respectively the pixel values of two adjacent pixels in the image, CC is the correlation coefficient of two adjacent pixels. As can be seen from Table 1, the adjacent pixels of the original images have a high correlation and the adjacent

Research on Multiple-image Encryption Scheme Based on … - Zhang Leihong et al. 321 (a) (b) FIG. 10. Histograms of plaintext and ciphertext (a) The histogram corresponding to the plaintext image; (b) The histogram corresponding to the ciphertext image. TABLE 1. Correlation coefficients of adjacent pixels to a plaintext image and a ciphertext image Correlation coefficient Horizontal Original lena Encrypted lena Original A Encrypted A 0.8358 0.0910 0.8424 0.0514 Vertical 0.6894 0.0241 0.8820 0.0398 Diagonal 0.6397 0.0123 0.8088 0.0258 (a) (c) (b) (d) FIG. 11. Scatter plots corresponding to plaintext and ciphertext: (a)(c) are scatter plots corresponding to different plaintext images; (b)(d) are scatter plots corresponding to different ciphertext images.

322 Current Optics and Photonics, Vol. 2, No. 4, August 2018 pixels of the ciphertext images have a small correlation, with the adjacent pixels are basically irrelevant, which shows that the statistical characteristics of the original images have been diffused into random ciphertext images. In the experiment, MATLAB software was used to simulate the correlation of adjacent pixels in the vertical direction, and the correlation was shown by a scatter plot, as shown in Fig. 11. Obviously, the correlation of adjacent pixels in the original image shows a clear linear relationship, while the correlation of adjacent pixels of the encrypted image presents a random correspondence. 3.2.2. Noise attack Noise attack is inevitable in the process of information encryption and propagation, and the noise will affect the imaging quality of the object and the transmission of the image information. Therefore, it is essential to evaluate the robustness of the encryption algorithm when the key or ciphertext is attacked by noise. Figure 12 shows the NC value of the reconstructed image under different noise attack intensities in the scheme of this paper. From the figure, we can see that: (1) With the increase of noise intensity, the NC value has a certain degree of decline; (2) Although a certain noise attack, the reconstructed image can still be distinguished, which shows that the scheme of this paper has effective security. 3.2.3. Compressibility analysis This paper makes full use of the anti-cutting characteristics of the Fourier transform algorithm, achieving information compression and greatly reducing the amount of information transmitted. In the experiment, the image information after Fourier transform was cut out at different proportions, and then the cropped images adopt compressive ghost imaging. Evaluating the cropped information with the quality of the FIG. 12. Reconstructed images under different noise attack intensities. reconstructed images will not affect the encryption algorithm in this paper. In this paper, similarity (NC) is used to objectively evaluate the degree of similarity between the original plaintext image and the reconstructed image. The obtained NC value is used as an objective index to evaluate the sharpness of the cut image reconstruction, so as to determine the maximum cut ratio of the plaintext image. The largest cutting ratio, thereby minimizing the amount of information transmitted, reducing storage space and increasing the rate of information transmission. For an image of size M × N, the mathematical expression of similarity NC is as follows:    ′               (13)          where X is the original plaintext image,  ′ is the recon- structed image for the cut image. In this experiment, we cut separately 30%, 50%, 75% of the graphic information after Fourier transform. Four 64 × 64 binary images were selected and the sampling rate was 50%. The reconstructed images are shown in Fig. 13 (taking one of the images as an example). Where (a) represents the original image; (b-e) are respectively the reconstructed images of 30%, 50%, and 75%, whose NC are respectively 0.8749, 0.7432, 0.5828. From the effect images of Fig. 13, it can be seen that the reconstructed images can recognize the contour of the original image when the cropping ratio reaches 75%. Therefore, it is illustrated that the algorithm can successfully reconstruct the original images. From Table 2, it can be seen that the amount of transmitted information is 2048 bits when the cutting ratio is 75%, which greatly reduces the amount of transmitted (a) (b) (c) (d) FIG. 13. Reconstructed images with different cut ratios. TABLE 2. NC values and transmitted information’s amount of reconstructed images in different cut ratios Percent of cutting (%) 30 50 75 Quantity of information 5734.4 4096 2048 NC 0.8749 0.7432 0.5828

资料库

基于傅里叶变换和鬼成像算法的多图像加密方案研究.pdf

相关推荐

安全技术

热门标签

最新资料