滚动轴承-转子系统非线性动力学建模.pdf-资料库

中国科技论文在线 http://www.paper.edu.cn 滚动轴承—转子系统非线性动力学建模# 白长青* （西安交通大学航天航空学院,机械结构强度与振动国家重点实验室，西安 710049） 5 摘要：考虑滚动轴承中滚珠与滚道间的间隙和轴承运行表面波纹度，提出用于研究滚动轴承 —转子系统动力特性的滚动轴承五自由度非线性动力学模型，其中引入了高速下滚珠离心力和陀螺力矩的影响。结合转子有限元法建立滚动轴承支撑的转子系统有限元模型，通过数值分析仿真和实验研究分析转子系统的非线性动力特性。实验数据和数值仿真结果是一致的，证实了所建立动力学模型的合理性。发现由于滚动轴承中 Hertzian 接触力、内间隙等非线性因素的影响，当转速达到系统临界转速的两倍时，激起了系统亚谐共振。关键词：滚动轴承；转子；非线性振动；亚谐共振中图分类号：O347.6 10 15 Nonlinear dynamic model of ball bearing-rotor system BAI Changqing (State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace, Xi’an Jiaotong University, Xi’an 710049) Abstract: In this paper, a ﬁve-degree-of-freedom nonlinear dynamic model is presented for studying the dynamic properties of ball bearing-rotor system supported by ball bearings under the effects of both internal clearance and bearing running surface waviness. The nonlinear dynamic model includes the high-speed effects of ball centrifugal force and gyroscopic moment. Using the finite element method to establish the finite element model of rotor system supported by ball bearings.Through the numerical approach and experimental research, the nonlinear dynamic behavior of ball bearing-rotor system is investigated. Numerical results of this research are in good agreement with experimental data, thus validating the proposed model. It is shown that the resonance frequency is provoked when the speed is about twice the synchroresonance frequency, while the subharmonic resonance occurs due to the nonlinearity of ball bearings which includes the Hertzian contact force, bearing internal clearance, and so on. Key words: ball bearing; rotor; nonlinear vibration; subharmonic resonance 20 25 30 0 引言滚动轴承是转动机械中的常用部件。由于其可靠性高、能耗低，火箭发动机、航空燃气涡轮机等尖端设备上常用它作为支承部件。随着运行可靠性和转速要求的不断提高，滚动轴 35 承支承的转子系统的振动分析变得越来越重要。作为振动源之一的滚动轴承具有多种非线性因素，如 Hertzian 接触力与变形间关系、变柔度（varying compliance）、内间隙、波纹度等等。从而引起了大量科研人员的关注。 40 Perret[1]和 Meldau[2]首先研究了变柔度对轴承静力平衡的影响。Jones[3]考虑滚珠离心力和陀螺力矩的影响提出了一个准静态平衡模型。Harris[4]在他的专著中总结了这些静态和准静态的轴承模型。Walters[5]研究了变柔度的动力影响，仿真了轴承保持架的运动。以他的工作为基础，Gupta[6]给出了滚动轴承和滚子轴承的动力学模型，指出动力学模型能避免准静态模型中存在的许多问题，以此进行转子轴承系统设计能显著减少总设计费用。Childs[7]在研究航天飞机发动机高压燃料涡轮泵的转子动力不稳定问题时，对涡轮泵的泵端和涡轮端轴基金项目：高等学校博士学科点专项科研基金（20090201120040）；国家自然科学基金（10902080，91016008）；作者简介：白长青，男，副教授，主要研究方向：非线性动力系统稳定性、非线性随机系统动力特性、多场耦合系统动态特性研究. E-mail: baichq@mail.xjtu.edu.cn - 1 -

中国科技论文在线 http://www.paper.edu.cn 承的刚度与转子转速之间的关系用三次多项式进行模拟 45 50 55 60 (1-1) 其中、、和为拟合系数。De Mul 等[8]提出用于计算滚动轴承中相关联的平衡载荷分布的 5DOF 模型，其中考虑了轴承间隙和滚珠的离心力。Liew 等人[9]总结了有间隙滚动轴承的 2DOF 和 5DOF 模型并阐明了滚珠离心力的影响，指出在高速轻载下应注意 5DOF 模型的显著影响。 Gustafsson 等人[10]的试验研究显示滚动轴承的内间隙是滚动体通过振动的一个重要参数。Yamamoto[11]给出了一个解析模型用于研究一个垂直转子的振动，支承该转子的是具有径向间隙的滚动轴承。Childs[12]用摄动法研究了非对称间隙对转子运动的影响。Saito[13]用数值谐波平衡法研究了一个不平衡 Jeffcott 转子中轴承径向间隙的影响。好几位研究人员用滚动轴承的两自由度（2DOF）动力学模型并考虑轴承内间隙的影响进行了转子系统的非线性仿真分析[14-17]。Mevel 等人[14]通过变动控制参数描述了通向混沌的不同路径。Tiwari 等在文献[15]中研究了由于滚动轴承内间隙影响造成的平衡转子系统的非线性行为，并随之在文献 [16]中研究了不平衡转子系统。Harsha 等人[17]用两自由度模型观察了滚动轴承表面波纹度和内间隙对平衡转子系统振动特性的影响，然后他们给出一个刚性转子系统的理论模型分析了不同滚珠数目和波纹度阶数影响下系统的非线性振动响应[18]。Bai 和 Xu[19]提出了一个广义的滚动轴承动力学模型并分析了滚动轴承支承的转子系统的动力特性。Aktüuk 等人[20]用一个三自由度系统分析了一对角接触球轴承支承的刚性转子的径向和轴向振动。文献[21]中对实际滚动轴承－液氢涡轮泵转子系统的动力特性进行数值模拟，发现滚动轴承会引起涡轮泵转子系统的亚谐共振，在转子系统设计中应该引起重视。但是这些研究大都通过 2DOF 数值分析研究滚动轴承－转子系统的非线性动力特性，并缺乏实验研究和相应的理论分析，影响 65 了对滚动轴承引起的转子系统非线性行为的深入认识，尤其是滚动轴承造成的转子系统亚谐共振现象。 1 滚动轴承 5DOF 模型为了研究转子轴承系统的动力特性，首先要确定非线性轴承支反力，然后才能给出系统的动力学微分方程。 70 1.1 坐标系和转换矩阵如图 1 所示，定义两个坐标系用于数值分析，固定在空间的惯性坐标系是正交系，原点在轴承（内圈）中心，轴沿轴承转子系统的转轴方向；有同样轴的局部滚动体坐标系固定在滚动体上，原点在内圈曲率中心的公称位置上。 - 2 - bk332210aaaakb0a1a2a3a),,(zyxzz),,(Zr

中国科技论文在线 http://www.paper.edu.cn 75 80 图 1 滚动轴承坐标系 Fig. 1. Ball bearing coordinate systems. 一般而言，轴承的运动和所受的载荷可以用五个自由度完全描述。轴承中心的位移向量可以在惯性坐标系中依据转子质量中心来定义，包含平动位移、、和角位移、的位移向量可以表示为滚动体的位置可以根据局部滚动体坐标系中内圈曲率中心的位移向量确定。对于第个滚珠，其位移向量为 . (1) 其中下标表示位移方向分布沿坐标轴；下标表示滚动体指示数。以下用变量 85 符号的上标表示各变量所处的时刻，为简化表达式，表示时间的上标均省略不写。依据小位移假设，考虑内间隙和波纹度的影响，滚动体的位移向量和轴承中心的位 . (2) 移向量之间的关系如下所示其中转换矩阵的表达式为 , (3) 90 (4) 是内、外圈的相对波纹度向量其中和分别表示轴承的径向和轴向波纹度；下标和分别指示内圈和外圈。 . (5) - 3 - UxyzxyUTyxzyxUjjuTjzjrjjuuuu,,zr,,zrjtjuUjjjWUTujTjjjijpjijpjijpjijpjjjφφφprφprφqzφqzφφTcossin000cos)(sin)(100cos)(sin)(0sincosjWT0)()(ojijojijjqqppWpqio

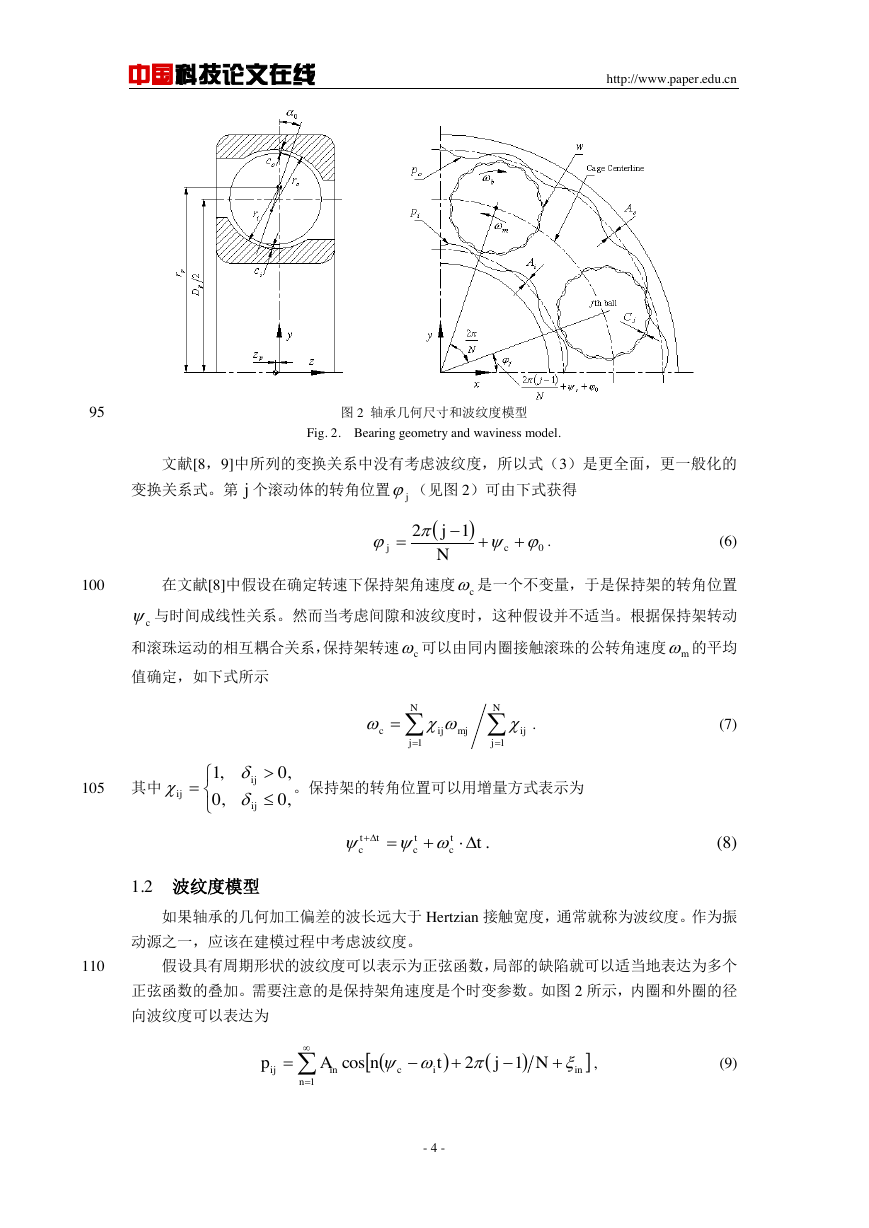
中国科技论文在线 http://www.paper.edu.cn 95 图 2 轴承几何尺寸和波纹度模型 Fig. 2. Bearing geometry and waviness model. 文献[8，9]中所列的变换关系中没有考虑波纹度，所以式（3）是更全面，更一般化的变换关系式。第个滚动体的转角位置（见图 2）可由下式获得 . (6) 100 在文献[8]中假设在确定转速下保持架角速度是一个不变量，于是保持架的转角位置与时间成线性关系。然而当考虑间隙和波纹度时，这种假设并不适当。根据保持架转动和滚珠运动的相互耦合关系，保持架转速可以由同内圈接触滚珠的公转角速度的平均值确定，如下式所示 . (7) 105 其中。保持架的转角位置可以用增量方式表示为 . (8) 1.2 波纹度模型如果轴承的几何加工偏差的波长远大于 Hertzian 接触宽度，通常就称为波纹度。作为振动源之一，应该在建模过程中考虑波纹度。 110 假设具有周期形状的波纹度可以表示为正弦函数，局部的缺陷就可以适当地表达为多个正弦函数的叠加。需要注意的是保持架角速度是个时变参数。如图 2 所示，内圈和外圈的径向波纹度可以表达为 , (9) - 4 - jj012cjNjcccmNjijNjmjijc11,0,0,0,1ijijijttctcttcinicninijNjtnAp12cos1

中国科技论文在线 http://www.paper.edu.cn (10) 115 其中是波纹度阶数；和分别是径向波纹度的振幅和初始相位角。内圈和外圈的轴向波纹度分别如下所示 , (11) . (12) 其中和分别是轴向波纹度的振幅和初始相位角。 120 如果滚珠与内、外圈接触点间的角度差为 180 度，与内、外圈接触的滚珠波纹度分别为 , (13) , (14) 其中和分别是滚珠波纹度的振幅和初始相位角。同式（8）相似，第个滚珠的转角位 125 置可由下式计算得到 , (15) 1.3 滚珠平衡方程假设滚动轴承的外圈固定而内圈和转轴一同转动，如图 3 所示。考虑内间隙、波纹度和滚珠超大量的影响，在公称位置（），滚珠中心和内外圈曲率中心间的公称 130 距离，和，分别如下 , (16) . (17) 滚动轴承在高速运转时，滚珠的离心力和陀螺力矩影响较大，在分析中需要考虑在内。如图 3 所示，因为滚珠运动产生的体积力的作用，滚珠与内外圈的接触角和不再相等。 135 几何关系如下所示 , (18) , (19) - 5 - onocnonojNjtnAp12cos1nAinicninijNjtnBq12cos1onocnonojNjtnBq12cos1BwnjbjnnjijnCw1cosnjbjnnjojnCw1cosCjbjttbjtbjttbjch0UiLoLiijjbiijcwhDrL2oojjboojcwhDrL2iorrijzzijijvuLvuL00cossintanrojzojojvLvL00cossintan

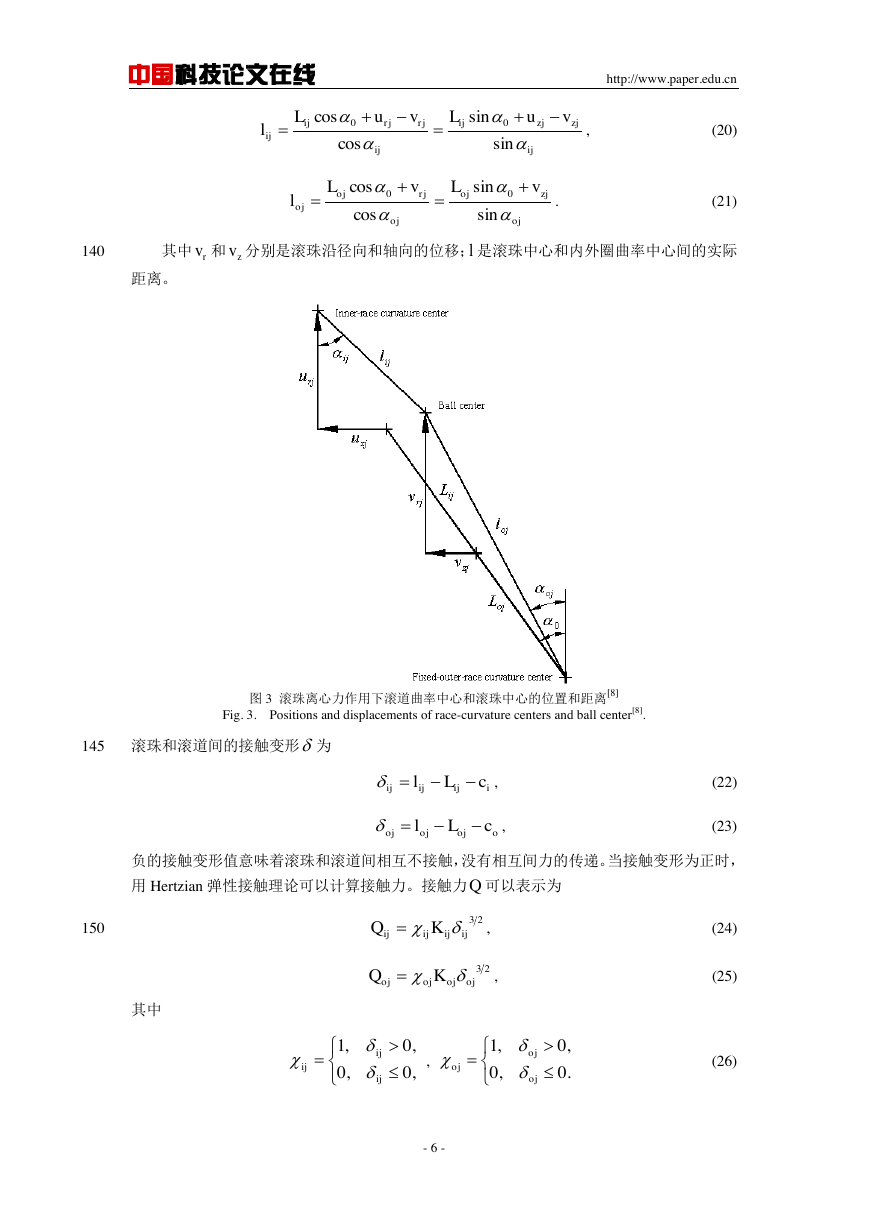
中国科技论文在线 http://www.paper.edu.cn , (20) . (21) 140 其中和分别是滚珠沿径向和轴向的位移；是滚珠中心和内外圈曲率中心间的实际距离。图 3 滚珠离心力作用下滚道曲率中心和滚珠中心的位置和距离[8] Fig. 3. Positions and displacements of race-curvature centers and ball center[8]. 145 滚珠和滚道间的接触变形为 , (22) , (23) 负的接触变形值意味着滚珠和滚道间相互不接触，没有相互间力的传递。当接触变形为正时，用 Hertzian 弹性接触理论可以计算接触力。接触力可以表示为 150 , (24) 其中 , (25) , (26) - 6 - ijzjzjijijrjrjijijvuLvuLlsinsincoscos00ojzjojojrjojojvLvLlsinsincoscos00rvzvliijijijcLloojojojcLlQ23ijijijijKQ23ojojojojKQ,0,0,0,1ijijij.0,0,0,1ojojoj

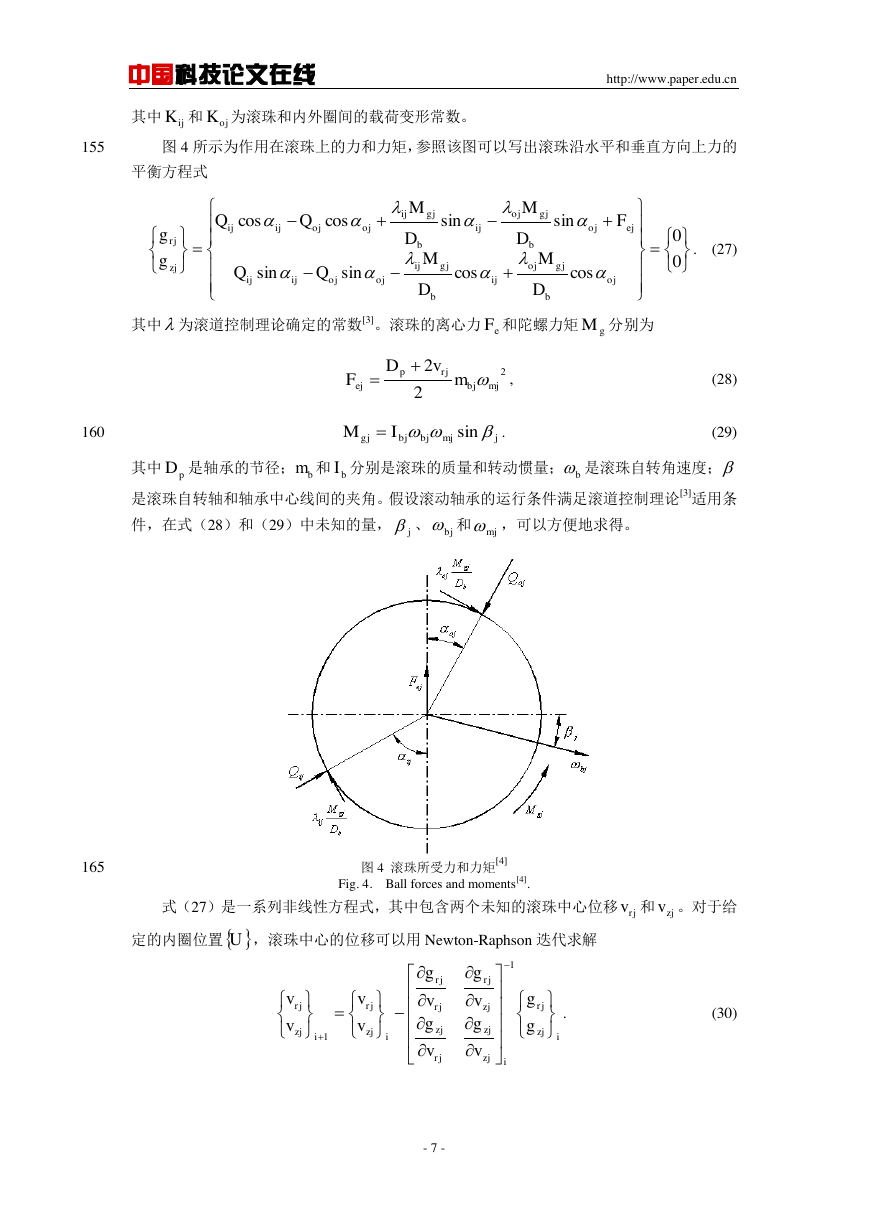
中国科技论文在线 http://www.paper.edu.cn 其中和为滚珠和内外圈间的载荷变形常数。 155 图 4 所示为作用在滚珠上的力和力矩，参照该图可以写出滚珠沿水平和垂直方向上力的平衡方程式 . (27) 其中为滚道控制理论确定的常数[3]。滚珠的离心力和陀螺力矩分别为 , (28) 160 . (29) 其中是轴承的节径；和分别是滚珠的质量和转动惯量；是滚珠自转角速度；是滚珠自转轴和轴承中心线间的夹角。假设滚动轴承的运行条件满足滚道控制理论[3]适用条件，在式（28）和（29）中未知的量，、和，可以方便地求得。 165 图 4 滚珠所受力和力矩[4] Fig. 4. Ball forces and moments[4]. 式（27）是一系列非线性方程式，其中包含两个未知的滚珠中心位移和。对于给定的内圈位置，滚珠中心的位移可以用 Newton-Raphson 迭代求解 . (30) - 7 - ijKojK00coscossinsinsinsincoscosojbgjojijbgjijojojijijejojbgjojijbgjijojojijijzjrjDMDMQQFDMDMQQggeFgM222mjbjrjpejmvDFjmjbjbjgjIMsinpDbmbIbjbjmjrjvzjvUizjrjizjzjrjzjzjrjrjrjizjrjizjrjggvgvgvgvgvvvv11

中国科技论文在线 170 1.4 接触力和动力学方程在局部滚动体坐标系中，第个滚动体所受的接触力可以表达为 http://www.paper.edu.cn . (31) 每个滚动体所受的接触力向量可以用转换矩阵转换为惯性坐标系下的当量力向量。对所有滚动体所受的当量力向量求和就能得到总的轴承支反力向量 175 . (32) 其中下标、和分别表示沿、和坐标轴方向。对如图 5 所示的转子轴承系统，采用转子有限元法离散转轴，其动力学方程可以表示为 (33) 其中、和分别为系统的刚度、质量和阻尼矩阵。和分别为系统所受 180 的重力载荷和不平衡力向量。图 5 滚动轴承转子系统示意图 Fig. 5. Sketch map of ball bearing-rotor system. 2 数值计算结果及试验对比 185 为验证数值分析结果和研究滚动轴承支承的不平衡转子系统的非线性动力特性，搭建相应的滚动轴承—转子系统试验台，其中转轴两边用相对放置的角接触球轴承 7200AC 支承，轴承参数见表 1。转盘的偏心量为 32 时，系统在 2000-10000 rpm 转速范围内，转盘沿垂直方向最大振幅的试验和数值计算结果如图 6 所示。可以发现测试数据和根据所建数学模型计算得到 190 的结果是一致的，特别是转速超过系统的正进动共振转速后。试验测得转子系统的正进动共振转速约为 3300 rpm，数值计算求得的共振转速为 3280 rpm。当转速达到系统共振转速的 - 8 - jibgjijijbgjijijijijbgjijijijjzjrjjrDMDMQDMQQQQQsinsinsincosjTFNjjjyxzyxQTMMFFFF1TTxyzxyztFFFUKUDUMugKMDgFuFeμm

资料库

滚动轴承-转子系统非线性动力学建模.pdf

相关推荐

开发技术

热门标签

最新资料