logo资料库

机器学习中的数学.pdf

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：1.22M 资料格式：pdf 举报 版权申诉
第1页 / 共34页
第2页 / 共34页
第3页 / 共34页
第4页 / 共34页
第5页 / 共34页
第6页 / 共34页
第7页 / 共34页
第8页 / 共34页
资料共34页，剩余部分请下载后查看
    机器学习中的数学(1)-回归(regression)、梯度下降(gradient descent) 版权声明： 本文由 LeftNotEasy 所有，发布于 http://leftnoteasy.cnblogs.com。如果转载，请注明出处，在未经作者 同意下将本文用于商业用途，将追究其法律责任。 前言: 上次写过一篇关于贝叶斯概率论的数学，最近时间比较紧，coding 的任务 比较重，不过还是抽空看了一些机器学习的书和视频，其中很推荐两个：一个 是 stanford 的 machine learning 公开课，在 verycd 可下载，可惜没有 翻译。不过还是可以看。另外一个是 prml-pattern recognition and machine learning, Bishop 的一部反响不错的书，而且是 2008 年的，算 是比较新的一本书了。 前几天还准备写一个分布式计算的系列，只写了个开头，又换到写这个系列 了。以后看哪边的心得更多，就写哪一个系列吧。最近干的事情比较杂，有跟 机器学习相关的，有跟数学相关的，也有跟分布式相关的。 这个系列主要想能够用数学去描述机器学习，想要学好机器学习，首先得去 理解其中的数学意义，不一定要到能够轻松自如的推导中间的公式，不过至少 得认识这些式子吧，不然看一些相关的论文可就看不懂了，这个系列主要将会 着重于去机器学习的数学描述这个部分，将会覆盖但不一定局限于回归、聚类、 分类等算法。 回归与梯度下降： 回归在数学上来说是给定一个点集，能够用一条曲线去拟合之，如果这个曲 线是一条直线，那就被称为线性回归，如果曲线是一条二次曲线，就被称为二 次回归，回归还有很多的变种，如 locally weighted 回归，logistic 回归， 等等，这个将在后面去讲。 用一个很简单的例子来说明回归，这个例子来自很多的地方，也在很多的 open source 的软件中看到，比如说 weka。大概就是，做一个房屋价值的 评估系统，一个房屋的价值来自很多地方，比如说面积、房间的数量（几室几 厅）、地段、朝向等等，这些影响房屋价值的变量被称为特征(feature)， feature 在机器学习中是一个很重要的概念，有很多的论文专门探讨这个东西。 在此处，为了简单，假设我们的房屋就是一个变量影响的，就是房屋的面积。 假设有一个房屋销售的数据如下： 面积(m^2) 销售价钱（万元） 123 250 150 320 87 160 102 220 … …
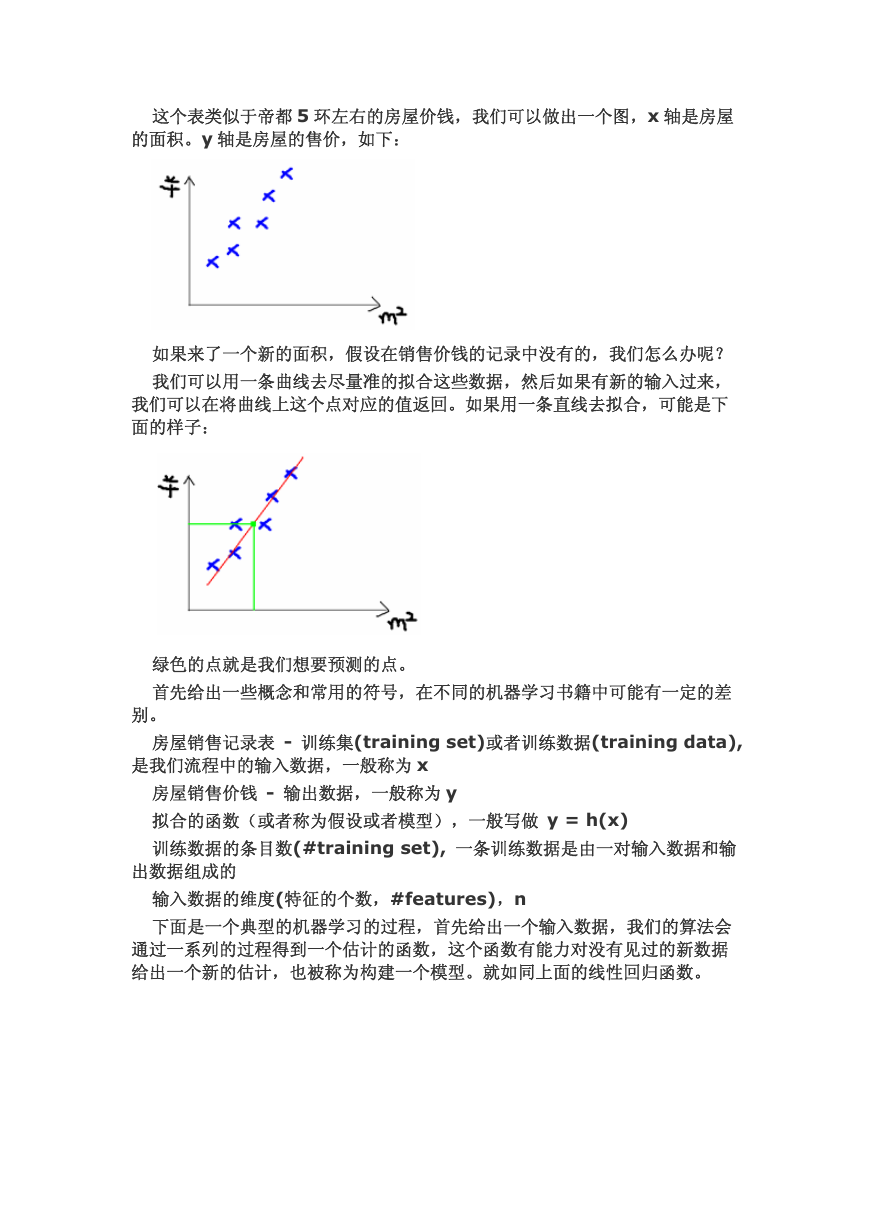
    这个表类似于帝都 5 环左右的房屋价钱，我们可以做出一个图，x 轴是房屋 的面积。y 轴是房屋的售价，如下： 如果来了一个新的面积，假设在销售价钱的记录中没有的，我们怎么办呢？ 我们可以用一条曲线去尽量准的拟合这些数据，然后如果有新的输入过来， 我们可以在将曲线上这个点对应的值返回。如果用一条直线去拟合，可能是下 面的样子： 绿色的点就是我们想要预测的点。 首先给出一些概念和常用的符号，在不同的机器学习书籍中可能有一定的差 别。 房屋销售记录表 - 训练集(training set)或者训练数据(training data), 是我们流程中的输入数据，一般称为 x 房屋销售价钱 - 输出数据，一般称为 y 拟合的函数（或者称为假设或者模型），一般写做 y = h(x) 训练数据的条目数(#training set), 一条训练数据是由一对输入数据和输 出数据组成的 输入数据的维度(特征的个数，#features)，n 下面是一个典型的机器学习的过程，首先给出一个输入数据，我们的算法会 通过一系列的过程得到一个估计的函数，这个函数有能力对没有见过的新数据 给出一个新的估计，也被称为构建一个模型。就如同上面的线性回归函数。
    我们用 X1，X2..Xn 去描述 feature 里面的分量，比如 x1=房间的面积， x2=房间的朝向，等等，我们可以做出一个估计函数： θ 在这儿称为参数，在这儿的意思是调整 feature 中每个分量的影响力， 就是到底是房屋的面积更重要还是房屋的地段更重要。为了如果我们令 X0 = 1，就可以用向量的方式来表示了： 我们程序也需要一个机制去评估我们 θ 是否比较好，所以说需要对我们做出 的 h 函数进行评估，一般这个函数称为损失函数（loss function）或者错误 函数(error function)，描述 h 函数不好的程度，在下面，我们称这个函数 为 J 函数 在这儿我们可以做出下面的一个错误函数： 这个错误估计函数是去对 x(i)的估计值与真实值 y(i)差的平方和作为错误 估计函数，前面乘上的 1/2 是为了在求导的时候，这个系数就不见了。 如何调整 θ 以使得 J(θ)取得最小值有很多方法，其中有最小二乘法(min square)，是一种完全是数学描述的方法，在 stanford 机器学习开放课最后 的部分会推导最小二乘法的公式的来源，这个来很多的机器学习和数学书上都 可以找到，这里就不提最小二乘法，而谈谈梯度下降法。 梯度下降法是按下面的流程进行的： 1）首先对 θ 赋值，这个值可以是随机的，也可以让 θ 是一个全零的向量。 2）改变 θ 的值，使得 J(θ)按梯度下降的方向进行减少。 为了更清楚，给出下面的图：
    这是一个表示参数 θ 与误差函数 J(θ)的关系图，红色的部分是表示 J(θ)有着比较高的取值，我们需要的是，能 够让 J(θ)的值尽量的低。也就是深蓝色的部分。θ0，θ1 表示 θ 向量的两个维 度。 在上面提到梯度下降法的第一步是给 θ 给一个初值，假设随机给的初值是在 图上的十字点。 然后我们将 θ 按照梯度下降的方向进行调整，就会使得 J(θ)往更低的方向 进行变化，如图所示，算法的结束将是在 θ 下降到无法继续下降为止。 非是全局最小点，可能是一个局部最小点，可能是下面的情况： 当然，可能梯度下降的最终点并
    上面这张图就是描述的一个局部最小点，这是我们重新选择了一个初始点得 到的，看来我们这个算法将会在很大的程度上被初始点的选择影响而陷入局部 最小点 下面我将用一个例子描述一下梯度减少的过程，对于我们的函数 J(θ)求偏导 J：（求导的过程如果不明白，可以温习一下微积分） 下面是更新的过程，也就是 θi 会向着梯度最小的方向进行减少。θi 表示更 新之前的值，-后面的部分表示按梯度方向减少的量，α 表示步长，也就是每次 按照梯度减少的方向变化多少。 一个很重要的地方值得 注意的是，梯度是有方向的，对于一个向量 θ，每一维分量 θi 都可以求出一个 梯度的方向，我们就可以找到一个整体的方向，在变化的时候，我们就朝着下 降最多的方向进行变化就可以达到一个最小点，不管它是局部的还是全局的。 用更简单的数学语言进行描述步骤 2）是这样的： 倒三角形表示梯度，按这种方式来表示，θi 就不 见了，看看用好向量和矩阵，真的会大大的简化数学的描述啊。 总结与预告： 本文中的内容主要取自 stanford 的课程第二集，希望我把意思表达清楚 了：）本系列的下一篇文章也将会取自 stanford 课程的第三集，下一次将会 深入的讲讲回归、logistic 回归、和 Newton 法，不过本系列并不希望做成 stanford 课程的笔记版，再往后面就不一定完全与 stanford 课程保持一致 了。
    机器学习中的数学(2)-线性回归，偏差、方差权衡 版权声明： 本文由 LeftNotEasy 所有，发布于 http://leftnoteasy.cnblogs.com。如果转载，请注明出处，在未经作者 同意下将本文用于商业用途，将追究其法律责任。如果有问题，请联系作者 wheeleast@gmail.com 前言： 距离上次发文章，也快有半个月的时间了，这半个月的时间里又在学习机器 学习的道路上摸索着前进，积累了一点心得，以后会慢慢的写写这些心得。写 文章是促进自己对知识认识的一个好方法，看书的时候往往不是非常细，所以 有些公式、知识点什么的就一带而过，里面的一些具体意义就不容易理解了。 而写文章，特别是写科普性的文章，需要对里面的具体意义弄明白，甚至还要 能举出更生动的例子，这是一个挑战。为了写文章，往往需要把之前自己认为 看明白的内容重新理解一下。 机器学习可不是一个完全的技术性的东西，之前和部门老大在 outing 的时 候一直在聊这个问题，机器学习绝对不是一个一个孤立的算法堆砌起来的，想 要像看《算法导论》这样看机器学习是个不可取的方法，机器学习里面有几个 东西一直贯穿全书，比如说数据的分布、最大似然（以及求极值的几个方法， 不过这个比较数学了），偏差、方差的权衡，还有特征选择，模型选择，混合 模型等等知识，这些知识像砖头、水泥一样构成了机器学习里面的一个个的算 法。想要真正学好这些算法，一定要静下心来将这些基础知识弄清楚，才能够 真正理解、实现好各种机器学习算法。 今天的主题是线性回归，也会提一下偏差、方差的均衡这个主题。 线性回归定义： 在上一个主题中，也是一个与回归相关的，不过上一节更侧重于梯度这个概 念，这一节更侧重于回归本身与偏差和方差的概念。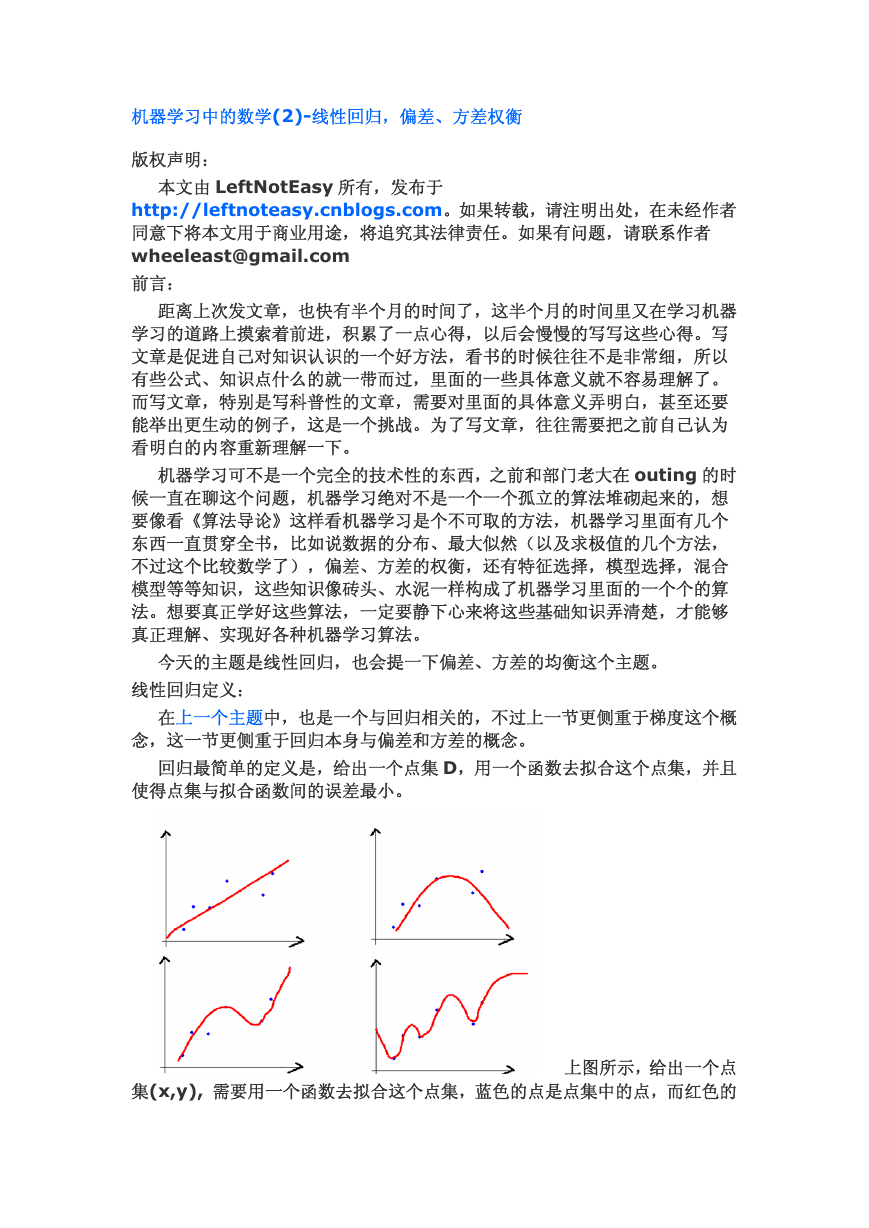 回归最简单的定义是，给出一个点集 D，用一个函数去拟合这个点集，并且 使得点集与拟合函数间的误差最小。 上图所示，给出一个点 集(x,y), 需要用一个函数去拟合这个点集，蓝色的点是点集中的点，而红色的
    曲线是函数的曲线，第一张图是一个最简单的模型，对应的函数为 y = f(x) = ax + b，这个就是一个线性函数， 第二张图是二次曲线，对应的函数是 y = f(x) = ax^2 + b。 第三张图我也不知道是什么函数，瞎画的。 第四张图可以认为是一个 N 次曲线，N = M - 1，M 是点集中点的个数， 有一个定理是，对于给定的 M 个点，我们可以用一个 M - 1 次的函数去完美的 经过这个点集。 真正的线性回归，不仅会考虑使得曲线与给定点集的拟合程度最好，还会考 虑模型最简单，这个话题我们将在本章后面的偏差、方差的权衡中深入的说， 另外这个话题还可以参考我之前的一篇文章：贝叶斯、概率分布与机器学习， 里面对模型复杂度的问题也进行了一些讨论。 线性回归(linear regression)，并非是指的线性函数，也就是 （为了方便起见，以后向量我就不在上面加箭 头了） x0,x1…表示一个点不同的维度，比如说上一节中提到的，房子的价钱是由 包括面积、房间的个数、房屋的朝向等等因素去决定的。而是用广义的线性函 数： wj 是系数，w 就是这个系数组成的向量， 它影响着不同维度的 Φj(x)在回归函数中的影响度，比如说对于房屋的售价来 说，房间朝向的 w 一定比房间面积的 w 更小。Φ(x)是可以换成不同的函数， 不一定要求 Φ(x)=x，这样的模型我们认为是广义线性模型。 最小二乘法与最大似然： 这个话题在此处有一个很详细的讨论，我这里主要谈谈这个问题的理解。最 小二乘法是线性回归中一个最简单的方法，它的推导有一个假设，就是回归函 数的估计值与真实值间的误差假设是一个高斯分布。这个用公式来表示是下面 的样子： ，y(x,w)就是给定了 w 系数向量下的回归函数的估 计值，而 t 就是真实值了，ε 表示误差。我们可以接下来推出下面的式子： 这是一个简单的条件概率表达式，表示在 给定了 x，w，β 的情况下，得到真实值 t 的概率，由于 ε 服从高斯分布，则从 估计值到真实值间的概率也是高斯分布的，看起来像下面的样子：
    贝叶斯、概率分布与机器学习这篇文 章中对分布影响结果这个话题讨论比较多，可以回过头去看看，由于最小二乘 法有这样一个假设，则会导致，如果我们给出的估计函数 y(x,w)与真实值 t 不是高斯分布的，甚至是一个差距很大的分布，那么算出来的模型一定是不正 确的，当给定一个新的点 x’想要求出一个估计值 y’，与真实值 t’可能就非常的 远了。 概率分布是一个可爱又可恨的东西，当我们能够准确的预知某些数据的分布 时，那我们可以做出一个非常精确的模型去预测它，但是在大多数真实的应用 场景中，数据的分布是不可知的，我们也很难去用一个分布、甚至多个分布的 混合去表示数据的真实分布，比如说给定了 1 亿篇网页，希望用一个现有的分 布（比如说混合高斯分布）去匹配里面词频的分布，是不可能的。在这种情况 下，我们只能得到词的出现概率，比如 p(的)的概率是 0.5，也就是一个网页 有 1/2 的概率出现“的”。如果一个算法，是对里面的分布进行了某些假设，那 么可能这个算法在真实的应用中就会表现欠佳。最小二乘法对于类似的一个复 杂问题，就很无力了 偏差、方差的权衡(trade-off)： 偏差(bias)和方差(variance)是统计学的概念，刚进公司的时候，看到每 个人的嘴里随时蹦出这两个词，觉得很可怕。首先得明确的，方差是多个模型 间的比较，而非对一个模型而言的，对于单独的一个模型，比如说: 这样的一个给定了具体系数的估计函数，是不能说 f(x)的方差是多少。而偏 差可以是单个数据集中的，也可以是多个数据集中的，这个得看具体的定义。 方差和偏差一般来说，是从同一个数据集中，用科学的采样方法得到几个不 同的子数据集，用这些子数据集得到的模型，就可以谈他们的方差和偏差的情 况了。方差和偏差的变化一般是和模型的复杂程度成正比的，就像本文一开始 那四张小图片一样，当我们一味的追求模型精确匹配，则可能会导致同一组数 据训练出不同的模型，它们之间的差异非常大。这就叫做方差，不过他们的偏 差就很小了，如下图所示：
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料