2016年湖南省永州市中考数学真题及答案.doc-资料库

2016 年湖南省永州市中考数学真题及答案一、选择题：本大题共 12 小题，每小题 4 分，共 48 分 1． ﹣ 的相反数的倒数是（） A． 1 B． ﹣ 1 C． 2016 D． ﹣ 2016 2．不等式组的解集在数轴上表示正确的是（） A． B． C． D． 3．下列图案中既是轴对称图形又是中心对称图形的是（） A． B． C． D． 4．下列运算正确的是（） A． ﹣ a• a 3=a 3B． ﹣ （ a 2） 2=a 4C． x﹣ x= D．（ ﹣ 2）（ +2 ） =﹣ 1 5．如图，将两个形状和大小都相同的杯子叠放在一起，则该实物图的主视图为（） A． B． C． D ．） 6．在 “ 爱我永州 ” 中学生演讲比赛中，五位评委分别给甲、乙两位选手的评分如下：甲： 8、 7、 9、 8、 8 乙： 7、 9、 6、 9、 9 则下列说法中错误的是（ A．甲、乙得分的平均数都是 8 B．甲得分的众数是 8，乙得分的众数是 9 C．甲得分的中位数是 9，乙得分的中位数是 6 D．甲得分的方差比乙得分的方差小 7．对下列生活现象的解释其数学原理运用错误的是（ A．把一条弯曲的道路改成直道可以缩短路程是运用了 “ 两点之间线段最短 ” 的原理 B．木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了 “ 直线外一点与直线上各点连接的所有线段中，垂线段最短 ” 的原理 C．将自行车的车架设计为三角形形状是运用了 “ 三角形的稳定性 ” 的原理 D．将车轮设计为圆形是运用了 “ 圆的旋转对称性 ” 的原理）

8．抛物线 y=x 2+2x+m ﹣ 1 与 x 轴有两个不同的交点，则 m 的取值范围是（ A． m＜ 2 B． m＞ 2 C． 0＜ m≤ 2 D． m＜ ﹣ 2 9．如图，点 D， E 分别在线段 AB ， AC 上， CD 与 BE 相交于 O 点，已知 AB=AC ，现添加以下的哪个条件仍不能判定 △ABE ≌△ ACD （）） A． ∠ B= ∠ C B． AD=AE C． BD=CE D． BE=CD 10 ．圆桌面（桌面中间有一个直径为 0.4m 的圆洞）正上方的灯泡（看作一个点）发出的光线照射平行于地面的桌面后，在地面上形成如图所示的圆环形阴影．已知桌面直径为 1.2m ，桌面离地面 1m ，若灯泡离地面 3m ，则地面圆环形阴影的面积是（） A． 0.324 πm 2B． 0.2 88 π m 2 C． 1.0 8 π m 2D． 0.72 πm 2 11 ．下列式子错误的是（ A． cos40 °=sin50 ° B． tan15 °• tan75 ° =1 C． sin 225 °+cos 225 ° =1 D ． sin6 0 ° =2sin30 ° 12 ．我们根据指数运算，得出了一种新的运算，如表是两种运算对应关系的一组实例：）指数运算新运算 2 1=2 2 2=4 2 3=8 log 22= log 24= lo g 28= 1 2 3 … … 3 1=3 3 2=9 3 3=27 log 33= log 39= log 327= 1 2 3 … … 根据上表规律，某同学写出了三个式子： ① log 216=4 ， ②log 525=5 ， ③log 2 =﹣ 1．其中正确的是（ A． ①② B． ①③ C． ②③ D． ①② ③ ）二、填空题：本大题共 8 小题，每小题 4 分，共 32 分 13 ．涔天河水库位于永州市江华瑶族自治县境内，其扩建工程是湖南省 “ 十二五 ” 期间水利建设的 “一号工程 ” ，也是国务院重点推进的重大工程，其中灌区工程总投资约 39 亿元．请将 3900000000 用科学记数法表示为 14 ．在 1， π ，， 2， ﹣ 3.2 这五个数中随机取出一个数，则取出的这个数大于 2 的概率是．． 15 ．已知反比例函数 y= 的图象经过点 A（ 1， ﹣ 2），则 k= ． 16 ．方程组的解是．

17 ．化简： ÷ = ． 18 ．如图，在 ⊙ O 中， A， B 是圆上的两点，已知 ∠ AOB=40 ° ，直径 CD ∥ AB ，连接 AC ，则 ∠ BAC = 度． 19 ．已知一次函数 y=kx+2k+3 的图象与 y 轴的交点在 y 轴的正半轴上，且函数值 y 随 x 的增大而减小，则 k 所有可能取得的整数值为 20 ．如图，给定一个半径长为 2 的圆，圆心 O 到水平直线 l 的距离为 d，即 OM= d ．我们把圆上到直线 l 的距离等于 1 的点的个数记为 m．如 d=0 时， l 为经过圆心 O 的一条直线，此时圆上有四个到直线 l 的距离等于 1 的点，即 m=4 ，由此可知：（ 1）当 d=3 时， m= （ 2）当 m=2 时， d 的取值范围是；．．三、解答题：本大题共 7 小题，共 79 分 21 ．计算： ﹣ （ 3﹣ π ） 0﹣ | ﹣ 3+2| 22 ．二孩政策的落实引起了全社会的关注，某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度，在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查，调查分别为非常赞同、赞同、无所谓、不赞同等四种态度，现将调查统计结果制成了如图两幅统计图，请结合两幅统计图，回答下列问题：（ 1）在这次问卷调查中一共抽取了（ 2）请补全条形统计图；（ 3）持 “不赞同 ” 态度的学生人数的百分比所占扇形的圆心角为（ 4）若该校有 3000 名学生，请你估计该校学生对父母生育二孩持 “ 赞同 ” 和 “ 非常赞同 ” 两种态度的人数之和．名学生， a= 度； %；

23 ．如图，四边形 ABCD 为平行四边形，∠ BAD 的角平分线 AE 交 CD 于点 F，交 BC 的延长线于点 E．（ 1）求证： BE =CD ；（ 2）连接 BF ，若 BF ⊥ AE ， ∠BEA=60 ° ， AB=4 ，求平行四边形 ABCD 的面积． 24 ．某种商品的标价为 400 元 /件，经过两次降价后的价格为 324 元 /件，并且两次降价的百分率相同．（ 1）求该种商品每次降价的百分率；（ 2）若该种商品进价为 300 元 /件，两次降价共售出此种商品 100 件，为使两次降价销售的总利润不少于 3210 元．问第一次降价后至少要售出该种商品多少件？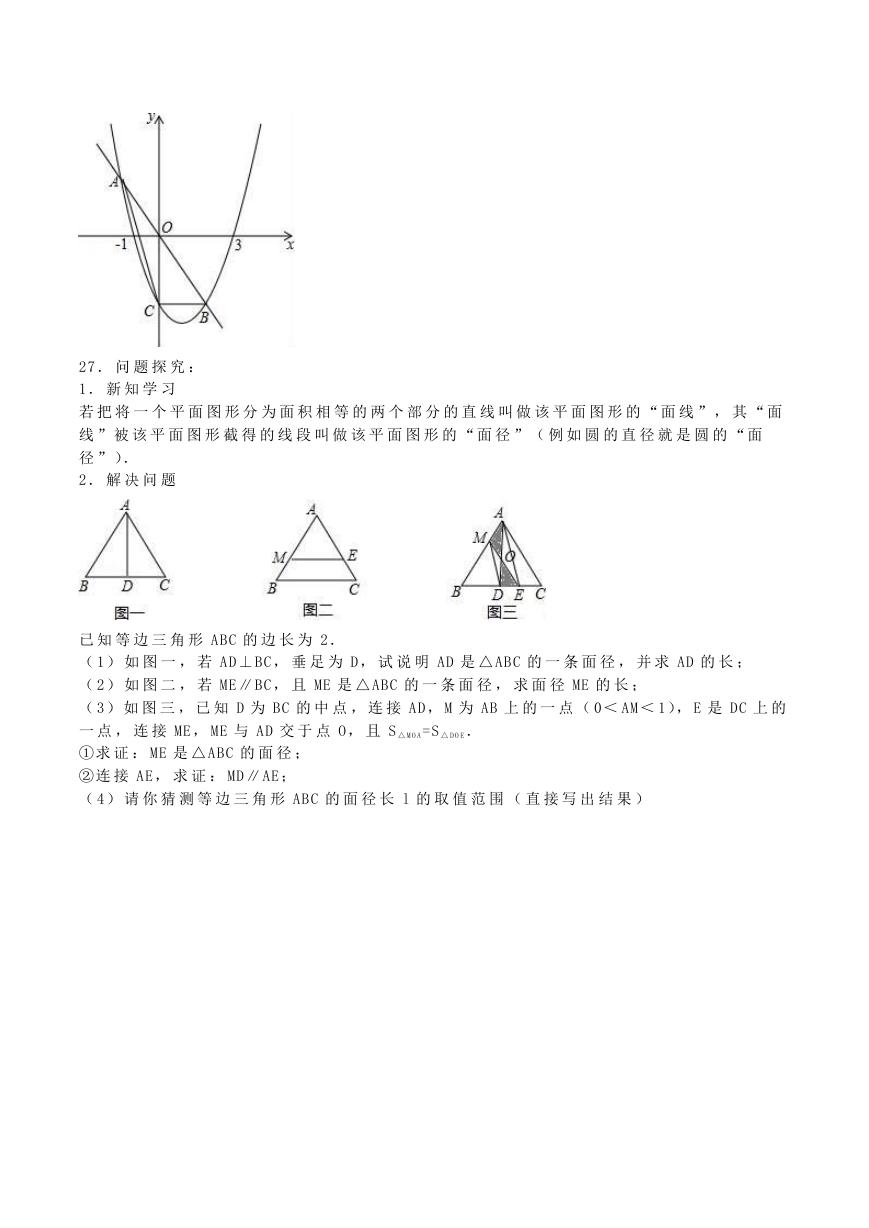 25 ．如图，△ AB C 是 ⊙O 的内接三角形，AB 为直径，过点 B 的切线与 AC 的延长线交于点 D， E 是 BD 中点，连接 CE ．（ 1）求证： CE 是 ⊙ O 的切线；（ 2）若 AC=4 ， BC =2 ，求 BD 和 CE 的长． 26 ．已知抛物线 y=ax 2 +bx ﹣ 3 经过（ ﹣ 1， 0），（ 3， 0）两点，与 y 轴交于点 C，直线 y=k x 与抛物线交于 A， B 两点．（ 1）写出点 C 的坐标并求出此抛物线的解析式；（ 2）当原点 O 为线段 AB 的中点时，求 k 的值及 A， B 两点的坐标；（ 3）是否存在实数 k 使得 △ ABC 的面积为？若存在，求出 k 的值；若不存在，请说明理由．

[来源:学+科+网] 27 ．问题探究： 1．新知学习若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的 “ 面线 ” ，其 “ 面线 ” 被该平面图形截得的线段叫做该平面图形的 “ 面径 ” （例如圆的直径就是圆的 “ 面径 ” ）． 2．解决问题已知等边三角形 ABC 的边长为 2．（ 1）如图一，若 AD ⊥ BC ，垂足为 D，试说明 AD 是 △ ABC 的一条面径，并求 AD 的长；（ 2）如图二，若 ME ∥ BC ，且 ME 是 △ ABC 的一条面径，求面径 ME 的长；（ 3）如图三，已知 D 为 BC 的中点，连接 AD ， M 为 AB 上的一点（ 0＜ AM ＜ 1）， E 是 DC 上的一点，连接 ME ， ME 与 AD 交于点 O，且 S △ M O A =S △ D O E ． ① 求证： ME 是 △ ABC 的面径； ② 连接 AE ，求证： MD ∥ AE ；（ 4）请你猜测等边三角形 ABC 的面径长 l 的取值范围（直接写出结果）

201 6 年湖南省永州市中考数学试卷参考答案与试题解析一、选择题：本大题共 12 小题，每小题 4 分，共 48 分 1． ﹣ 的相反数的倒数是（） A． 1 B． ﹣ 1 C． 2016 D． ﹣ 2016 【考点】倒数；相反数．【分析】直接利用相反数的概念以及倒数的定义分析，进而得出答案．【解答】解： ﹣ 的相反数是：， ∵ × 201 6=1 ， ∴ ﹣ 的相反数的倒数是： 2016 ．故选： C ． 2．不等式组的解集在数轴上表示正确的是（） A． B． C． D．【考点】解一元一次不等式组；在数轴上表示不等式的解集．【分析】把各不等式的解集在数轴上表示出来即可．【解答】解：不等式组的解集在数轴上表示为：．故选 A． 3．下列图案中既是轴对称图形又是中心对称图形的是（） A． B． C． D．【考点】中心对称图形；轴对称图形．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解： A、是轴对称图形．也是中心对称图形，故此选项正确； B、是轴对称图形，不是中心对称图形，故此选项错误； C、是轴对称图形，不是中心对称图形，故此选项错误； D、是轴对称图形，不是中心对称图形，故此选项错误．故选： A ．

4．下列运算正确的是（） A． ﹣ a• a 3=a 3B． ﹣ （ a 2） 2=a 4C． x﹣ x= D．（ ﹣ 2）（ +2 ） =﹣ 1 【考点】二次根式的混合运算；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．【分析】利用同底数的幂的乘法法则、幂的乘方、合并同类项法则，以及平方差公式即可判断．【解答】解： A、 ﹣ a•a 3=﹣ a 4 ，故选项错误； B、 ﹣ （ a 2） 2=﹣ a 4，选项错误； C、 x﹣ x= x，选项错误； D、（ ﹣ 2）（ +2 ） =（） 2﹣ 2 2=3 ﹣ 4= ﹣ 1，选项正确．故选 D． 5．如图，将两个形状和大小都相同的杯子叠放在一起，则该实物图的主视图为（） A． B． C． D ．【考点】简单组合体的三视图．【分析】根据图形的三视图的知识，即可求得答案．【解答】解：该实物图的主视图为．故选 B． 6．在 “ 爱我永州 ” 中学生演讲比赛中，五位评委分别给甲、乙两位选手的评分如下：甲： 8、 7、 9、 8、 8 乙： 7、 9、 6、 9、 9 则下列说法中错误的是（ A．甲、乙得分的平均数都是 8 B．甲得分的众数是 8，乙得分的众数是 9 C．甲得分的中位数是 9，乙得分的中位数是 6 D．甲得分的方差比乙得分的方差小【考点】方差；算术平均数；中位数；众数．【分析】分别求出甲、乙的平均数、众数、中位数及方差可逐一判断．）

【解答】解： A、 = =8 ， = =8 ，故此选项正确； B、甲得分次数最多是 8 分，即众数为 8 分，乙得分最多的是 9 分，即众数为 9 分，故此选项正确； C、 ∵ 甲得分从小到大排列为： 7、 8、 8、 8、 9， ∴ 甲的中位数是 8 分； ∵ 乙得分从小到大排列为： 6、 7、 9、 9、 9， ∴ 乙的中位数是 9 分；故此选项错误； D、 ∵ = × [（ 8﹣ 8） 2+（ 7﹣ 8） 2+ （ 9﹣ 8） 2+（ 8 ﹣ 8） 2+（ 8﹣ 8） 2]= × 2=0.4 ， = ×[ （ 7﹣ 8） 2+（ 9 ﹣ 8） 2+（ 6﹣ 8） 2+（ 9﹣ 8） 2+（ 9﹣ 8） 2]= × 8=1.6 ， ∴ ＜，故 D 正确；故选： C ．） 7．对下列生活现象的解释其数学原理运用错误的是（ A．把一条弯曲的道路改成直道可以缩短路程是运用了 “ 两点之间线段最短 ” 的原理 B．木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了 “ 直线外一点与直线上各点连接的所有线段中，垂线段最短 ” 的原理 C．将自行车的车架设计为三角形形状是运用了 “ 三角形的稳定性 ” 的原理 D．将车轮设计为圆形是运用了 “ 圆的旋转对称性 ” 的原理【考点】圆的认识；线段的性质：两点之间线段最短；垂线段最短；三角形的稳定性．【分析】根据圆的有关定义、垂线段的性质、三角形的稳定性等知识结合生活中的实例确定正确的选项即可．【解答】解：A、把一条弯曲的道路改成直道可以缩短路程是运用了 “ 两点之间线段最短 ” 的原理，正确； B、木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了 “ 两点确定一条直线 ” 的原理，故错误； C、将自行车的车架设计为三角形形状是运用了 “ 三角形的稳定性 ” 的原理，正确； D、将车轮设计为圆形是运用了 “ 圆的旋转对称性 ” 的原理，正确，故选 B． 8．抛物线 y=x 2+2x+m ﹣ 1 与 x 轴有两个不同的交点，则 m 的取值范围是（ A． m＜ 2 B． m＞ 2 C． 0＜ m≤ 2 D． m＜ ﹣ 2 【考点】抛物线与 x 轴的交点．【分析】由抛物线与 x 轴有两个交点，则 △ =b 2﹣ 4ac ＞ 0，从而求出 m 的取值范围．【解答】解： ∵ 抛物线 y=x 2 +2x +m ﹣ 1 与 x 轴有两个交点， ∴△ =b 2﹣ 4ac ＞ 0，即 4﹣ 4m+4 ＞ 0，解得 m＜ 2，故选 A．） 9．如图，点 D， E 分别在线段 AB ， AC 上， CD 与 BE 相交于 O 点，已知 AB=AC ，现添加以下的哪个条件仍不能判定 △ABE ≌△ ACD （）

资料库

2016年湖南省永州市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料