2008年山东青岛农业大学理论力学考研真题.doc

发布时间：2022-09-15 发布人：admin 分类：说明书资料大小：0.40M 资料格式：doc 举报版权申诉

第1页 / 共6页

第2页 / 共6页

第3页 / 共6页

第4页 / 共6页

第5页 / 共6页

第6页 / 共6页

文本预览

2008 年山东青岛农业大学理论力学考研真题 2、刚体作定轴转动，其上某点 A 到转轴距离为 R，为求出刚体上任意点在某一瞬时的速度和加速度的大小，下列那组条件是不充分的:（） A：已知 A 点的速度及该点的全加速度的方向； B：已知 A 点的法向加速度及该点的速度； C：已知 A 点的法向加速度及该点的全加速度的方向； D：已知 A 点的法向加速度和切向加速度 3、水平梁 AB 由三根直杆支承，载荷和尺寸如图。为了求出三根直杆的约束反力，可采用以下（）所示的平衡方程。 A：∑MA=0，∑Fx=0，∑Fy=0 B：∑MA=0，∑MC=0，∑Fy=0 C：∑MA=0，∑MC=0，∑MD=0 D：∑MA=0，∑MC=0，∑MB=0

7、正方形平板在自身平面内运动，若其顶点 A、B、C、D 的加速度大小相等，方向如图（ａ）、（ｂ）表示，则______________。 A：（ａ）、（ｂ）两种运动都可能； B：（ａ）、（ｂ）两种运动都不可能； C：（ａ）运动不可能，（ｂ）运动可能； D：（ａ）运动可能，（ｂ）运动不可能。

9 图示正方体，在 A 点作用两力 F1、F2，分别沿两条棱的方向，则下面说法不正确的是（）。 A：能通过 B 点加一个适当的力，使力系平衡； B：能通过 B 点，在 BCDE 平面内加一个适当的力，使力系简化为一个合偶； C：能通过 B 点，在 BCDE 平面内加一个适当的力，使力系简化为一个力螺旋 D：能通过 B 点，在 BCDE 平面内加一个适当的力，使力系简化为一个合力。

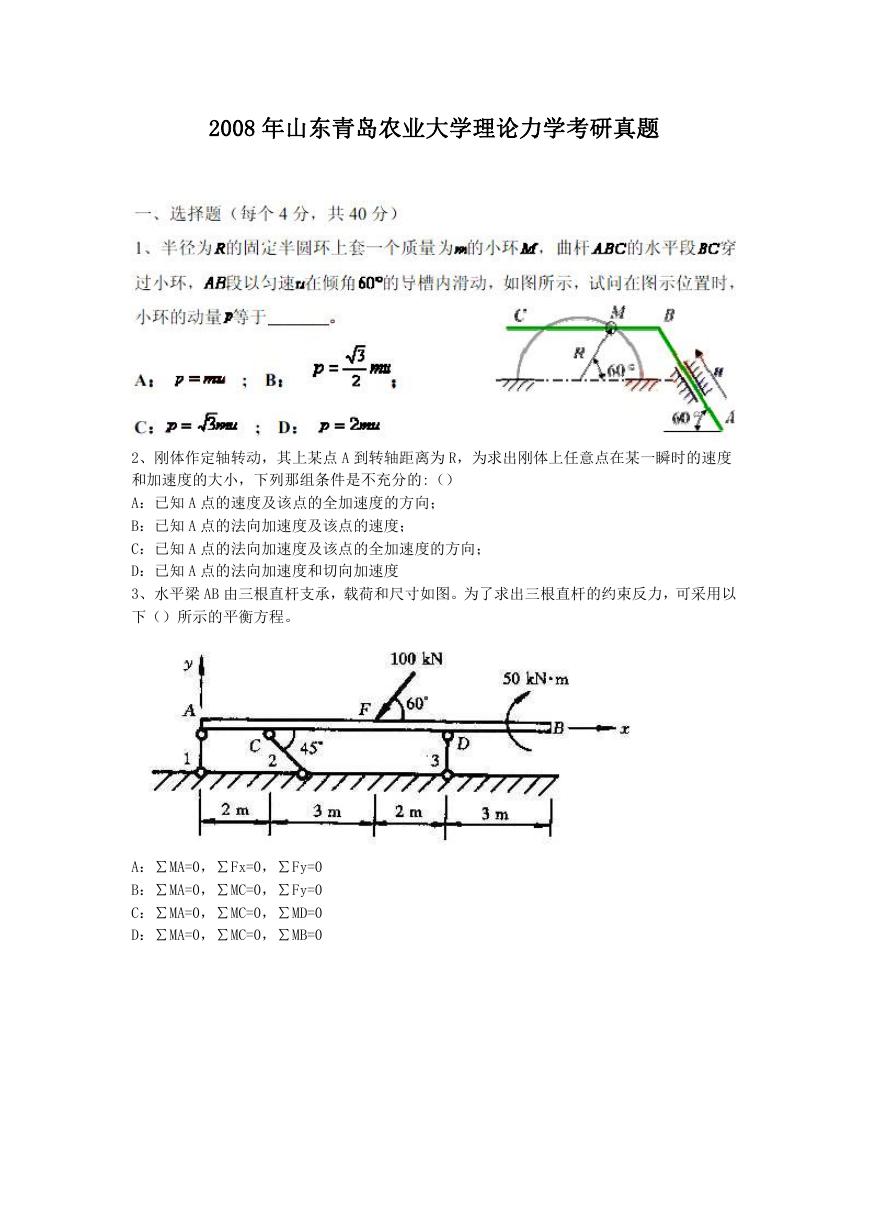
10、两个质量相同的质点，初速度相同，任一瞬时的切向加速度大小也相同，各沿不同的光滑曲线运动，则下列说法正确的是（）； A：任一瞬时两质点的受力相同； B：任一瞬时两质点的动量相同； C：在同一时间内，外力对两质点所作功相同； D：在同一时间内，两质点所受外力冲量相同。二、填空题（本题满分 20 分） 1、图示结构受矩为 M=10kN.m 的力偶作用。若 a=1m，各杆自重不计。则固定铰支座 D 的反力的大小为__________，方向__________。 2、在平面机构中，杆 AB=2L，以匀角速度ω1，绕 A 轴转动，而 CD 以匀角速度ω2 绕 B 轴转动，BD=BC=1.5L，在图示瞬时 AB 垂直 CD，若取 AB 为动参考体，则此时 D 点的牵连速度大小为；牵连加速度大小为；科氏加速度大小为（方向均需在图上画出） 5、图所示桁架中杆 HI、EG、AC 的内力分别是__________；__________；__________； __________。

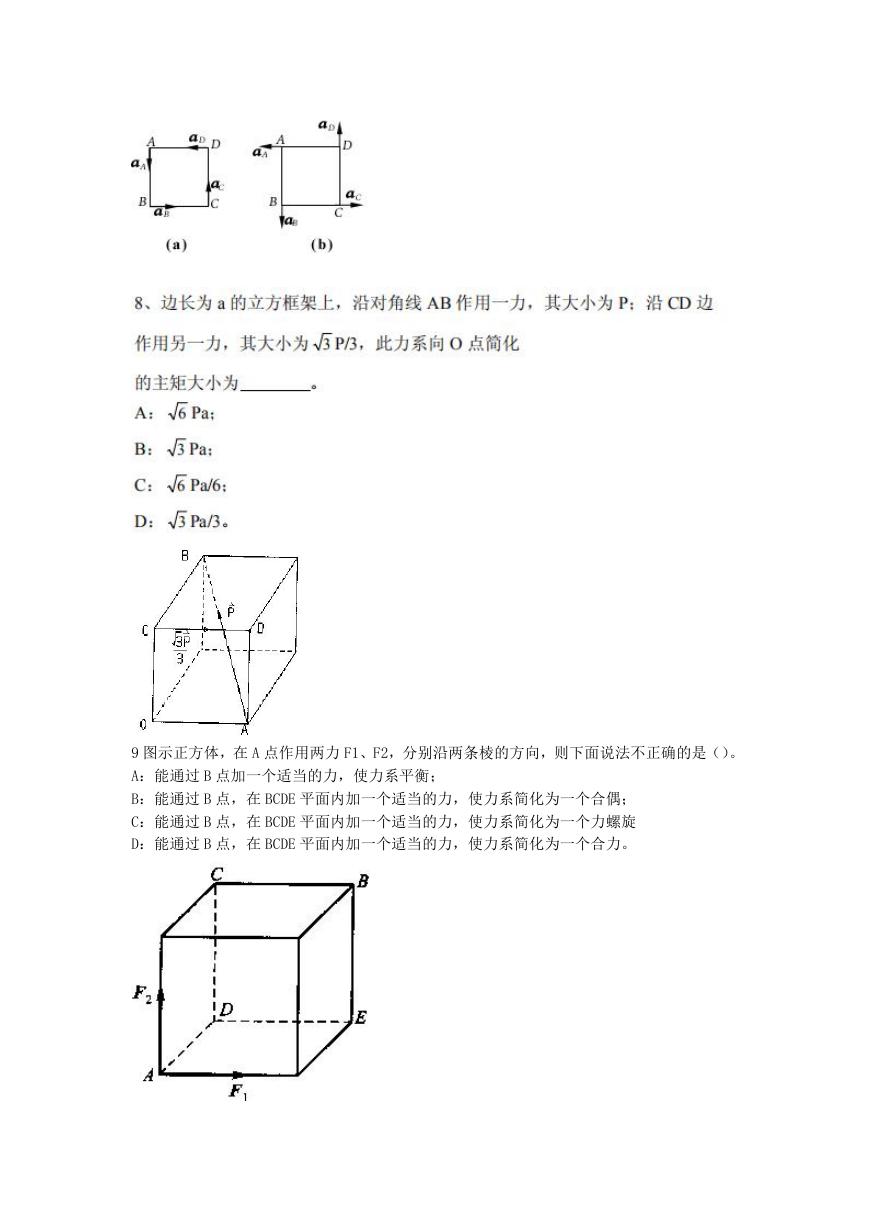
三、如题图所示，曲杆 ABC 与直杆 AED 用铰 A 及连杆 DC 相连，轮 C 重不计。已知：轮半径 R=1m,EG 段绳水平，P=100kN,L=1m，各杆重均不计。试求：①DEA 杆在 D、A 两处所受的约束力；②CBA 杆在 B、A 两处所受的约束力。（25 分）四、在图示平面机构中，曲柄 O1A 以匀角速度ω绕 O1 轴转动，连杆 AB 的中点 C 铰接一套筒 C，套筒可在摇杆 OD 上滑动，从而带动摇杆绕 O 轴摆动。已知 O1A=O2B=r，O1O2=AB。当曲柄 O1A 在图示铅垂位置时，θ=60°，OC=2r。试求该瞬时摇杆 OD 的角速度和角加速度。（20 分）

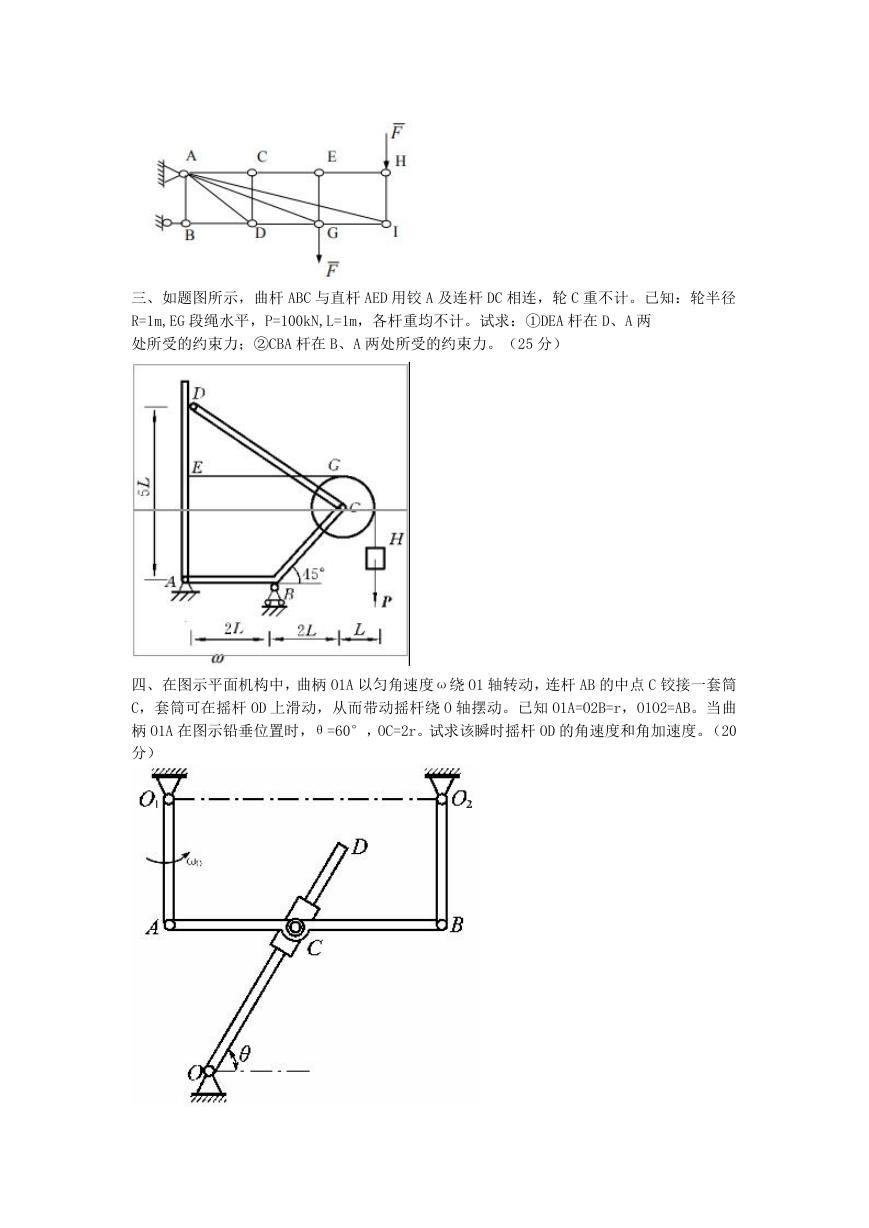
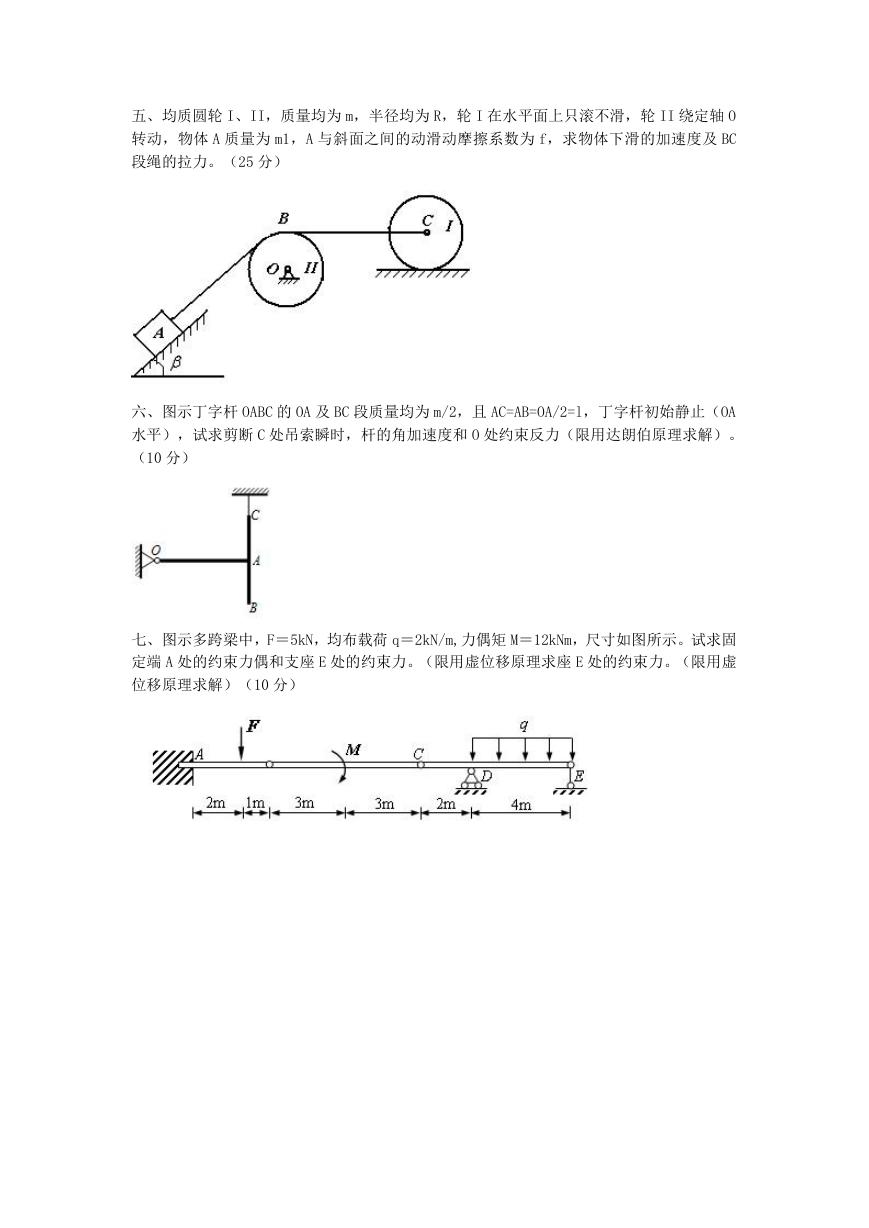
五、均质圆轮 I、II，质量均为 m，半径均为 R，轮 I 在水平面上只滚不滑，轮 II 绕定轴 O 转动，物体 A 质量为 m1，A 与斜面之间的动滑动摩擦系数为 f，求物体下滑的加速度及 BC 段绳的拉力。（25 分）六、图示丁字杆 OABC 的 OA 及 BC 段质量均为 m/2，且 AC=AB=OA/2=l，丁字杆初始静止（OA 水平），试求剪断 C 处吊索瞬时，杆的角加速度和 O 处约束反力（限用达朗伯原理求解）。（10 分）七、图示多跨梁中，F＝5kN，均布载荷 q＝2kN/m,力偶矩 M＝12kNm，尺寸如图所示。试求固定端 A 处的约束力偶和支座 E 处的约束力。（限用虚位移原理求座 E 处的约束力。（限用虚位移原理求解）（10 分）

分享到：

赞收藏

资料库

2008年山东青岛农业大学理论力学考研真题.doc

相关推荐

考研

热门标签

最新资料