读懂电感的气隙，气隙的计算方法和实际意义意义.pdf-资料库

kzqcsdn-11155773-4744302542948163969.pdf-第1页.png

第1页 / 共9页

kzqcsdn-11155773-4744302542948163969.pdf-第2页.png

第2页 / 共9页

kzqcsdn-11155773-4744302542948163969.pdf-第3页.png

第3页 / 共9页

kzqcsdn-11155773-4744302542948163969.pdf-第4页.png

第4页 / 共9页

kzqcsdn-11155773-4744302542948163969.pdf-第5页.png

第5页 / 共9页

kzqcsdn-11155773-4744302542948163969.pdf-第6页.png

第6页 / 共9页

kzqcsdn-11155773-4744302542948163969.pdf-第7页.png

第7页 / 共9页

kzqcsdn-11155773-4744302542948163969.pdf-第8页.png

第8页 / 共9页

一、电感储能描述电感储能的实质为周围磁场的储能，以磁性导磁材料如铁氧体、非晶、纳米晶以及磁粉芯等闭合磁芯电感所产生的磁场被限制在特定空间内，这个特定空间一般均为磁芯介质，这类的磁场分布形式我们这里就称为“规则磁场”分布，规则磁场大大简化了磁场计算的复杂性，如下图是磁芯电感的示意图。电感的储能也就是以磁介质为载体的周围磁场储能，磁场被限制在如图磁芯介质的红色虚线。二、电感储能定量表达式——电能转换为磁能的磁能积首先回顾一下电感的储能，电源中的储能电感常常涉及到从电能到磁能的过程转化，电能的表达式是我们熟悉的“电流”、“电压”以及“时间”的关系；那么我们用什么来描述电感对磁场的储能呢？这里需要引出磁能积，因为磁能积描述了能量和磁场以及磁芯体积的一种关系，磁能—磁能积的表达对于我们来说可能就陌生一些，这个前面我们专门讲过一节，这里做一些简单的回顾。如下是一种磁芯电感，假设电感线圈两端感应电动势为“u”，电流为“i”，我们计算一下电能“E”输入：上式（1）中，包含电流，对于这种规则磁场，连接电流和磁场的关系便是“安培环路定理”，表达式如下，磁场是“H”：电能表达式（1）上式（1）中，也包含了电压，对于这种规则磁场，连接电压和磁场的关系便是“法拉第电磁感应定律”，表达式如下：安培环路定理表达式（2）法拉第电磁感应定律（3）结合上面（1）、（2）及（3）得出如下式

表达式（4）描述了磁能是磁场与磁芯体积的关系，始终 Ve 表示磁芯有效体积，是磁路和磁芯截面积的乘积磁能积表达式（4）上面 uc 磁导率是磁芯材料的“绝对磁导率”不可与相对磁导率搞混淆，需要记住储能是磁场引发的磁场密度的储能，所以磁导率是材料的绝对磁导率，是磁芯材料的属性。磁芯有效体积表达式（5）相对磁导率“relative”和磁芯磁导率“core”（6）三、磁芯存储能量和气隙存储能量如下图，假定没有散磁通，则磁芯磁通密度和气隙磁通密度相等，根据磁阻最小磁通路径原理磁芯截面积和气隙截面积同样也是相等的。这里假定磁芯的气隙是两半对称磁芯中间用非磁性物质如环氧垫片隔出来的等效气隙，对于将磁芯部分磨掉产生的气隙形式，由于气隙相比磁芯有效长度很小，下面推导的表达式同样也是适用的。磁芯存储能量如下表达式气隙存储能量如下表达式磁芯存储能量表达式（7）磁芯和磁芯气隙总存储能量表达式磁芯气隙存储能量表达式（8）空气稀释系数“Z” 对于表达式（8）总能量中“等效磁路长度”表达式如下总存储能量表达式（8）

加入气隙的等效磁路长度（9）加入气隙的等效磁路长度（10）四、磁芯存储能量和气隙存储能量的总能量结合表达式（8）和表达式（10）得到空气“稀释”后的磁通密度的磁场总储能 E 为稀释系数“Z”表达式（11）总能量和稀释系数“Z”的关系表达式（12） 1、空气稀释系数 Z=1 的特殊取值意义借用表达式（12）式中稀释系数“Z=1”，那么得到如下表达式，这个表明 Z=1 时能量全部存储在磁芯中总能量和稀释系数“Z=1”的关系表达式（13）其实稀释系数“Z=1”时，还有一层含义，即当 Z=1 时，由于相对磁导率“ur”不可能为零，那么只能是“气隙长度”为零，下式可以说明。稀释系数“Z=1”的气隙长度表达式（14） 2、气隙和磁芯能量的比值关系及意义当 Z=1 时，如下表达式（15）气隙存储能量 Eg 必然为零。同样也说明了，没有气隙时，能量全部存储于磁芯中。当然气隙是很小的，但是你也清楚，一般磁性材料的磁芯的相对磁导率是非常大的，比如天通的 TP4 铁氧体常温下相对磁导率 ur=2300 左右，一般非晶及纳米晶 ur=4000 及以上，那么这将是对气隙的“千倍级”的放大。因此气隙虽小，但存储能量却是巨大的。

3、气隙和总能量的比值关系气隙储能和磁芯储能的关系比值（15）气隙储能和总储能的关系比值（16）从表达式（12）可以看出，加入气隙，总能量以“稀释系数 Z”倍数增长，从（15）和（16）可知且能量几乎都存储在气隙当中，磁芯能量得以“膨胀”增长。强调一下虽然我们看出（12），加入气隙后能量以稀释系数倍增长，但我们要明确，气隙越大相应的磁芯有效磁导率会越小，相同电流下磁通密度是减小的，所以增加气隙扩大能量存储是由条件的，接下来我们会用控制变量法说明问题。 4、有效磁导率 ue 介绍首先介绍一下加入气隙后的有效磁导率，空气“稀释系数 Z”是贯穿整个气隙储能电感的核心参数，其最本质的内容就是对良导磁材料磁导率的稀释变化，得到一种“适中”的磁材料（适中既有空气特性—储能不饱和以及良好的线性磁导率，又有良导磁材料特性—大电感量和强磁感应），从而即可以满足电感量要求，同时也可以满足安全储能要求。定义有效磁导率：从表达式（12）变换得到有效磁导率表达式，表达式如下有效磁导率 ue 表达式（16）从表达式（16）再次说明，当“Z=1”时，说明磁芯中没有加入任何气隙，磁芯材料+空气的中庸材料就变为“原材料”——纯磁芯材料介质。五、气隙或空气储能、磁芯储能以及总储能的控制变量分析对于磁芯和空气储能的关系说明，首先要回顾一下安培环路定理，H 是磁场安培环路定理表达式（17）加入气隙，磁芯被空气稀释后，磁芯磁导率发生变化，从表达式（16）有效磁导率得到磁通密度或者将安培环路定理做变换同样也可得到，如下图是磁芯开气隙后的示意图磁通密度表达式（18）

有效磁导率导出磁通密度表达式（19）可知，当磁材料被稀释后，得到有效磁导率或稀释磁导率“ue”，之后再得到稀释磁通密度 “B”—（这样一个递进关系），（19）式中，依旧“Z=1”表示没有加入任何气隙，随着气隙的加入磁通密度是不断减小的，这里一定要明确气隙长度和磁导率以及磁通密度的关系。接下来，我们在进一步将前面表达式（12）总能量表达式加以展开，分析能量的变化趋势及能量变化的影响因素：将表达式（19）带入表达式（12）得到总能量 E 表达式的另外一种安匝表达式同理得到磁芯储能 Ec 安匝表达式总能量安匝表达式（20）也可以得到气隙能量 Eg 的安匝表达式磁芯存储能量安匝表达式（21）气隙存储能量安匝表达式（22）上面得到三者能量的关系表达式，基于（20）、（21）及（22）安匝表达式控制变量分析能量变化趋势 1、保持安匝数（N*i）不变，承当保持电流“安（A，电流本是由负载决定的），匝数（N，电感线圈匝数）”二者不变时，即设定为常数，不断增加气隙时，能量关系图如下：可以看出随着气隙系数的增大，总存储能量 E 是减小的总储能 E 与气隙稀释系数 Z 之间的关系

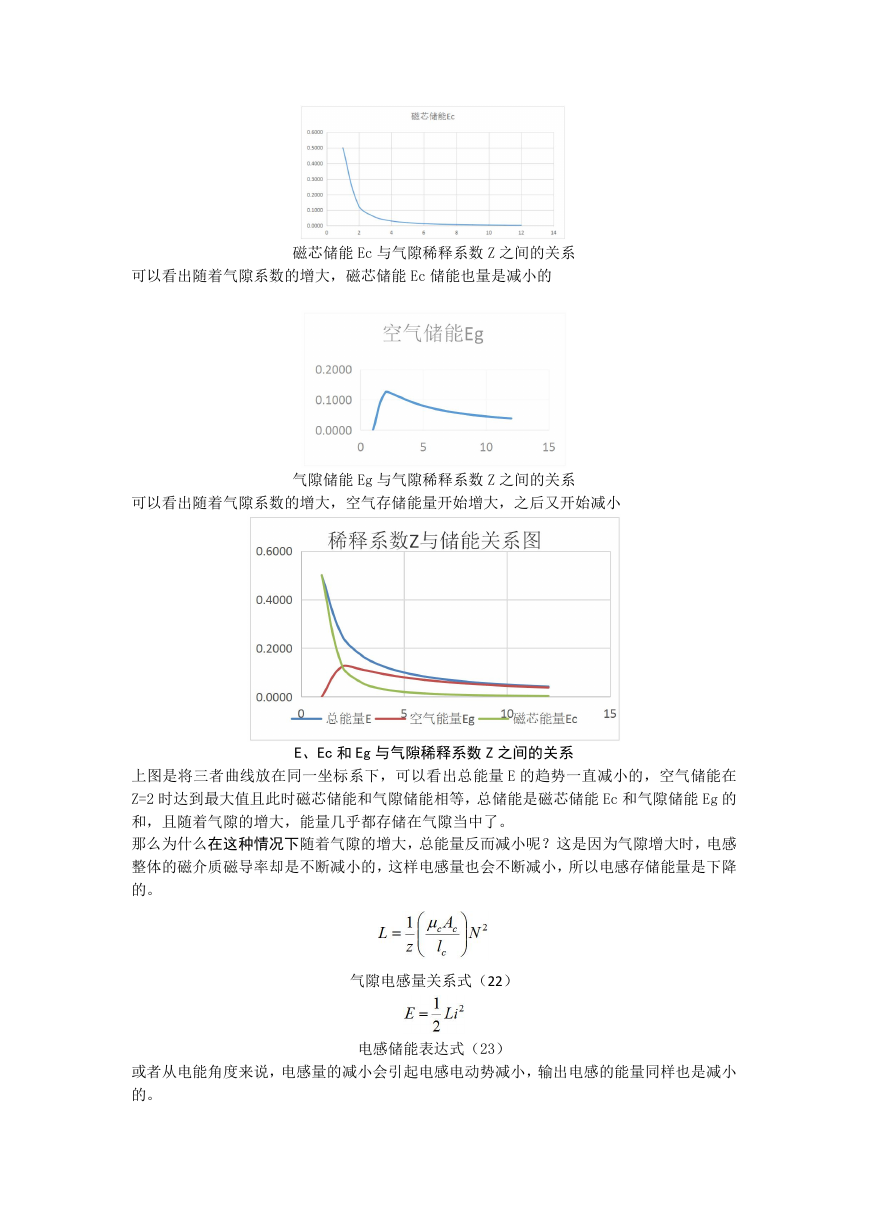
可以看出随着气隙系数的增大，磁芯储能 Ec 储能也量是减小的磁芯储能 Ec 与气隙稀释系数 Z 之间的关系可以看出随着气隙系数的增大，空气存储能量开始增大，之后又开始减小气隙储能 Eg 与气隙稀释系数 Z 之间的关系 E、Ec 和 Eg 与气隙稀释系数 Z 之间的关系上图是将三者曲线放在同一坐标系下，可以看出总能量 E 的趋势一直减小的，空气储能在 Z=2 时达到最大值且此时磁芯储能和气隙储能相等，总储能是磁芯储能 Ec 和气隙储能 Eg 的和，且随着气隙的增大，能量几乎都存储在气隙当中了。那么为什么在这种情况下随着气隙的增大，总能量反而减小呢？这是因为气隙增大时，电感整体的磁介质磁导率却是不断减小的，这样电感量也会不断减小，所以电感存储能量是下降的。气隙电感量关系式（22）电感储能表达式（23）或者从电能角度来说，电感量的减小会引起电感电动势减小，输出电感的能量同样也是减小的。

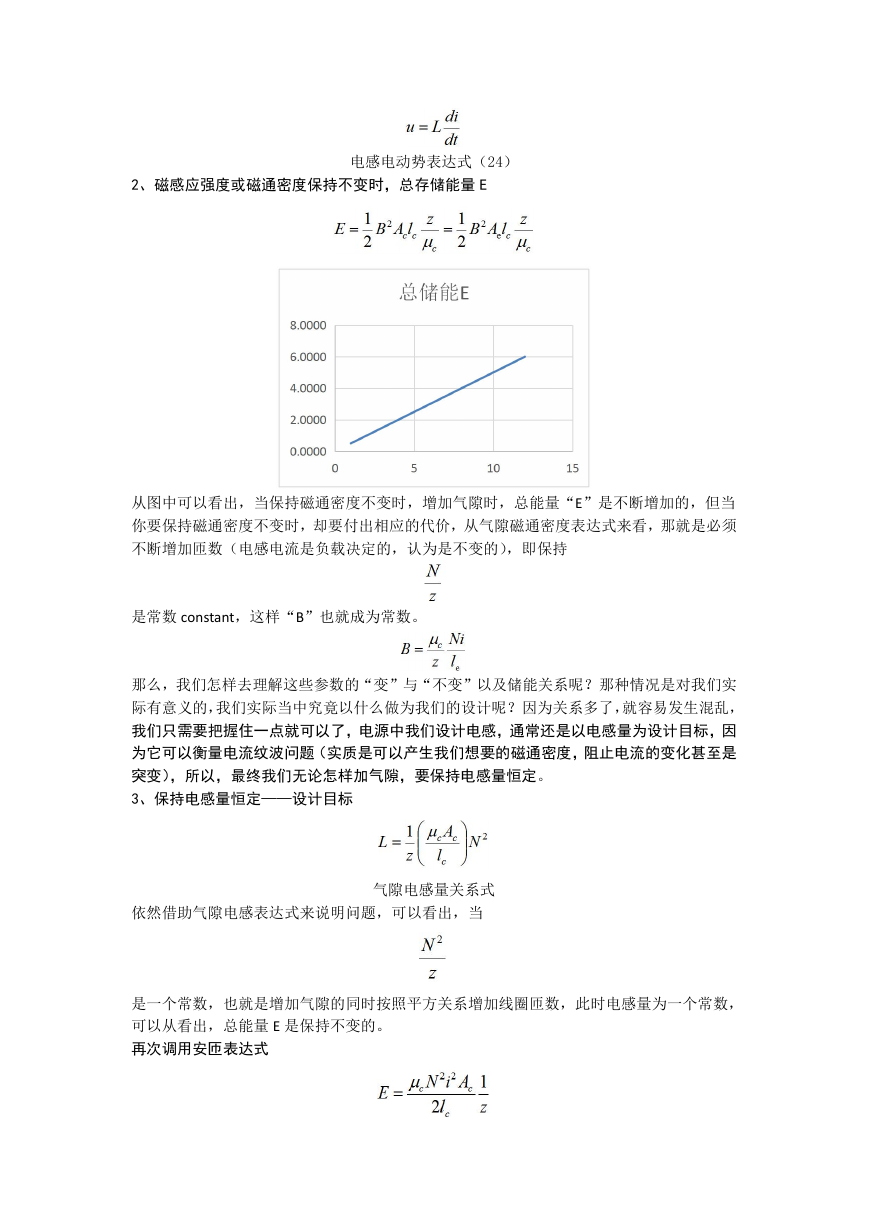
2、磁感应强度或磁通密度保持不变时，总存储能量 E 电感电动势表达式（24）从图中可以看出，当保持磁通密度不变时，增加气隙时，总能量“E”是不断增加的，但当你要保持磁通密度不变时，却要付出相应的代价，从气隙磁通密度表达式来看，那就是必须不断增加匝数（电感电流是负载决定的，认为是不变的），即保持是常数 constant，这样“B”也就成为常数。那么，我们怎样去理解这些参数的“变”与“不变”以及储能关系呢？那种情况是对我们实际有意义的，我们实际当中究竟以什么做为我们的设计呢？因为关系多了，就容易发生混乱，我们只需要把握住一点就可以了，电源中我们设计电感，通常还是以电感量为设计目标，因为它可以衡量电流纹波问题（实质是可以产生我们想要的磁通密度，阻止电流的变化甚至是突变），所以，最终我们无论怎样加气隙，要保持电感量恒定。 3、保持电感量恒定——设计目标依然借助气隙电感表达式来说明问题，可以看出，当气隙电感量关系式是一个常数，也就是增加气隙的同时按照平方关系增加线圈匝数，此时电感量为一个常数，可以从看出，总能量 E 是保持不变的。再次调用安匝表达式

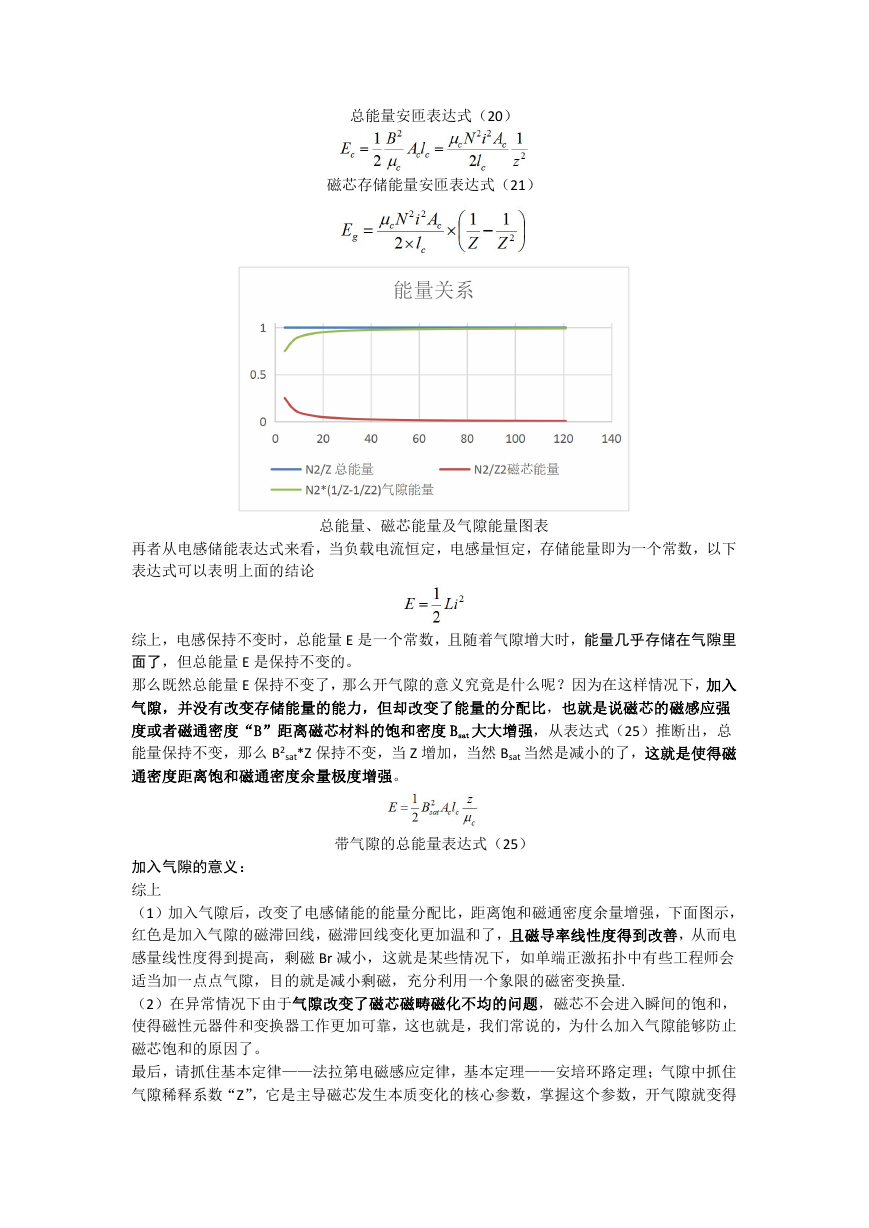
总能量安匝表达式（20）磁芯存储能量安匝表达式（21）总能量、磁芯能量及气隙能量图表再者从电感储能表达式来看，当负载电流恒定，电感量恒定，存储能量即为一个常数，以下表达式可以表明上面的结论综上，电感保持不变时，总能量 E 是一个常数，且随着气隙增大时，能量几乎存储在气隙里面了，但总能量 E 是保持不变的。那么既然总能量 E 保持不变了，那么开气隙的意义究竟是什么呢？因为在这样情况下，加入气隙，并没有改变存储能量的能力，但却改变了能量的分配比，也就是说磁芯的磁感应强度或者磁通密度“B”距离磁芯材料的饱和密度 Bsat 大大增强，从表达式（25）推断出，总能量保持不变，那么 B2 sat*Z 保持不变，当 Z 增加，当然 Bsat 当然是减小的了，这就是使得磁通密度距离饱和磁通密度余量极度增强。带气隙的总能量表达式（25）加入气隙的意义：综上（1）加入气隙后，改变了电感储能的能量分配比，距离饱和磁通密度余量增强，下面图示，红色是加入气隙的磁滞回线，磁滞回线变化更加温和了，且磁导率线性度得到改善，从而电感量线性度得到提高，剩磁 Br 减小，这就是某些情况下，如单端正激拓扑中有些工程师会适当加一点点气隙，目的就是减小剩磁，充分利用一个象限的磁密变换量. （2）在异常情况下由于气隙改变了磁芯磁畴磁化不均的问题，磁芯不会进入瞬间的饱和，使得磁性元器件和变换器工作更加可靠，这也就是，我们常说的，为什么加入气隙能够防止磁芯饱和的原因了。最后，请抓住基本定律——法拉第电磁感应定律，基本定理——安培环路定理；气隙中抓住气隙稀释系数“Z”，它是主导磁芯发生本质变化的核心参数，掌握这个参数，开气隙就变得

资料库

读懂电感的气隙，气隙的计算方法和实际意义意义.pdf

相关推荐

开发技术

热门标签

最新资料