Adaboost学习文档.pdf

发布时间：2022-05-31 发布人：admin 分类：说明书资料大小：1.11M 资料格式：pdf 举报版权申诉

z_feng12489-10780336-16359647274506202875.pdf-第1页.png

第1页 / 共9页

z_feng12489-10780336-16359647274506202875.pdf-第2页.png

第2页 / 共9页

z_feng12489-10780336-16359647274506202875.pdf-第3页.png

第3页 / 共9页

z_feng12489-10780336-16359647274506202875.pdf-第4页.png

第4页 / 共9页

z_feng12489-10780336-16359647274506202875.pdf-第5页.png

第5页 / 共9页

z_feng12489-10780336-16359647274506202875.pdf-第6页.png

第6页 / 共9页

z_feng12489-10780336-16359647274506202875.pdf-第7页.png

第7页 / 共9页

z_feng12489-10780336-16359647274506202875.pdf-第8页.png

第8页 / 共9页

文本预览

1.8 AdaBoost算法当做重要决定时，大家可能都会考虑吸取多个专家而不只是一个人的意见。那么机器学习处理的问题也是这样。这就是元算法（乭乥乴乡中乡乬乧乯乲乩乴乨乭）背后的思路。元算法是对其他算法进行组合的一种方式。接下来我们将集中关注一个称作乁乤乡乂乯乯乳乴的最流行的元算法。由于某些人认为乁乤乡乂乯乯乳乴是最好的监督学习的方法，所以该方法是机器学习工具箱中最强有力的工具之一。首先讨论不同分类器的集成方法（乢乡乧乧乩乮乧），然后主要关注乢乯乯乳乴乩乮乧方法及其代表分类器乁乤乡乢乯乯乳乴。乁乤乡乂乯乯乳乴算法将应用在上述单层决策树分类器之上。将在一个难数据集上应用乁乤乡乂乯乯乳乴分类器，以了解该算法是如何迅速超越其他分类器的。 1.8.1 集成方法我们自然可以将不同的分类器组合，而这种组合结果则被称为集成方法（乥乮乳乥乭乢乬乥乭乥乴乨乯乤）或者元算法（乭乥乴乡中乡乬乧乯乲乩乴乨乭）。使用集成方法时会有多种形式：可以是不同算法的集成，也可以是同一算法在不同设置下的集成，还可以是数据集不同部分分配给不同分类器之后的集成。 bagging : 基基基于于于数数数据据据重重重抽抽抽样样样的的的分分分类类类器器器方方方法法法自举汇聚法（乢乯乯乴乳乴乲乡买乡乧乧乲乥乧乡乴乩乮乧），也称为乢乡乧乧乩乮乧方法，是在从原始数据集选择乓次后得到乓个新数据集的一种技术。新数据集和原数据集的大小相等。每个数据集都是通过在原始数据集中随机选择一个样本来进行替换而得到的①。这里的替换就意味着可以多次地选择同一样本。这一性质就允许新数据集中可以有重复的值，而原始数据集的某些值在新集合中则不再出现。在乓个数据集建好之后，将某个学习算法分别作用于每个数据集就得到了乓个分类器。当我们要对新数据进行分类时，就可以应用这乓个分类器进行分类。与此同时，选择分类器投票结果中最多的类别作为最后的分类结果。当然，还有一些更先进的乢乡乧乧乩乮乧方法，比如随机森林（乲乡乮乤乯乭书乯乲乥乳乴）。 boosting : 基基基于于于错错错误误误提提提升升升分分分类类类器器器性性性能能能乢乯乯乳乴乩乮乧是一种与乢乡乧乧乩乮乧很类似的技术。不论是在乢乯乯乳乴乩乮乧还是乢乡乧乧乩乮乧当中，所使用的多个分类器的类型都是一致的。但是在前者当中，不同的分类器是通过串行训练而获得的，每个新分类器都根据已训练出的分类器的性能来进行训练。乢乯乯乳乴乩乮乧是通过集中关注被已有分类器错分的那些数据来获得新的分类器。因乢乯乯乳乴乩乮乧分类的结果是基于所有分类器的加权求和结果的，乢乯乯乳乴乩乮乧与乢乡乧乧乩乮乧不太一样。乢乡乧乧乩乮乧中的分类器权重是相等的，而乢乯乯乳乴乩乮乧中的分类器权重并不相等，每个权重代表的是其对应分类器在上一轮迭代中的成功度。丸丶

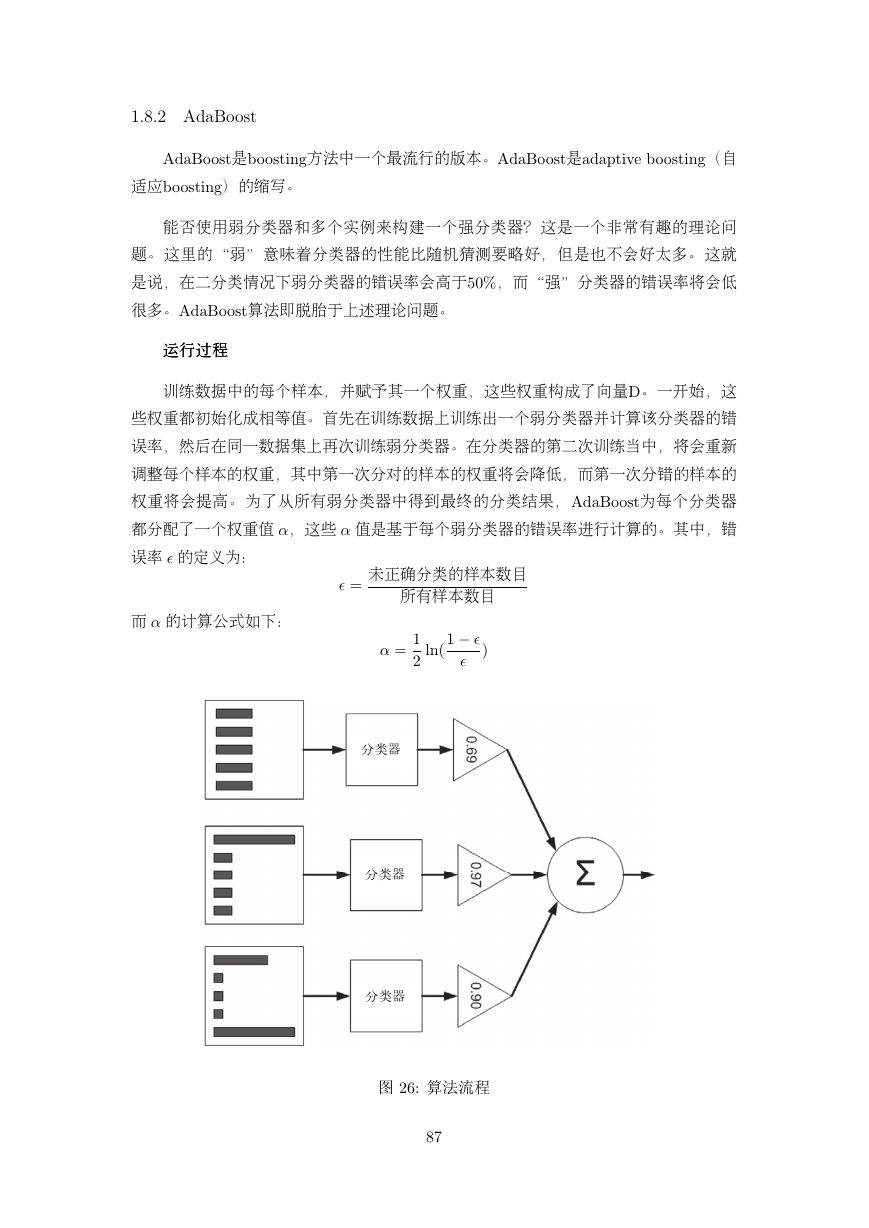
丽而 α 的计算公式如下：未正确分类的样本数目 1.8.2 AdaBoost 乁乤乡乂乯乯乳乴是乢乯乯乳乴乩乮乧方法中一个最流行的版本。乁乤乡乂乯乯乳乴是乡乤乡买乴乩乶乥乢乯乯乳乴乩乮乧（自适应乢乯乯乳乴乩乮乧）的缩写。能否使用弱分类器和多个实例来构建一个强分类器？这是一个非常有趣的理论问题。这里的“弱”意味着分类器的性能比随机猜测要略好，但是也不会好太多。这就是说，在二分类情况下弱分类器的错误率会高于丵丰严，而“强”分类器的错误率将会低很多。乁乤乡乂乯乯乳乴算法即脱胎于上述理论问题。运运运行行行过过过程程程训练数据中的每个样本，并赋予其一个权重，这些权重构成了向量乄。一开始，这些权重都初始化成相等值。首先在训练数据上训练出一个弱分类器并计算该分类器的错误率，然后在同一数据集上再次训练弱分类器。在分类器的第二次训练当中，将会重新调整每个样本的权重，其中第一次分对的样本的权重将会降低，而第一次分错的样本的权重将会提高。为了从所有弱分类器中得到最终的分类结果，乁乤乡乂乯乯乳乴为每个分类器都分配了一个权重值 α，这些 α 值是基于每个弱分类器的错误率进行计算的。其中，错误率的定义为：所有样本数目丱 − 丩丱串乬乮丨 α 丽图串丶为算法流程丸丷

计算出 α 值之后，可以对权重向量乄进行更新，以使得那些正确分类的样本的权重降低而错分样本的权重升高。乄的计算方法如下。 D(t)e−α i D i D D(t)eα D(t+1) i 丽 D(t+1) i 丽该样本被正确分类该样本被错误分类在计算出乄之后，乁乤乡乂乯乯乳乴又开始进入下一轮迭代。乁乤乡乂乯乯乳乴算法会不断地重复训练和调整权重的过程，直到训练错误率为丰或者弱分类器的数目达到用户的指定值为止。 AdaBoost训训训练练练误误误差差差界界界乁乤乡乂乯乯乳乴算法最终分类器的训练误差界为 N i=1 丱 N I丨G丨xi丩丽 yi丩 ≤ 丱 N i 乥乸买丨−yif 丨xi丩丩丽 m Zm AdaBoost 算算算法法法还还还有有有另另另一一一个个个解解解释释释，，，即即即可可可以以以认认认为为为 AdaBoost 算算算法法法是是是模模模型型型为为为加加加法法法模模模型型型、、、损损损失失失函函函数数数为为为指指指数数数函函函数数数、、、学学学习习习算算算法法法为为为前前前向向向分分分步步步算算算法法法时时时的的的二二二分分分类类类学学学习习习方方方法法法。。。乁乤乡乂乯乯乳乴算法是前向分步加法算法的特例．这时，模型是由基本分类器组成的加法模型，损失函数是指数函数。 1.8.3 实战：实现Adaboost基于决策树桩 AdaBoost的的的一一一般般般流流流程程程 (1) 收收收集集集数数数据据据：可以使用任意方法。 (2) 准准准备备备数数数据据据：依赖于所使用的弱分类器类型，本章使用的是单层决策树，这种分类器可以处理任何数据类型。当然也可以使用任意分类器作为弱分类器。作为弱分类器，简单分类器的效果更好。 (3) 分分分析析析数数数据据据：可以使用任意方法。 (4) 训训训练练练算算算法法法：乁乤乡乂乯乯乳乴的大部分时间都用在训练上，分类器将多次在同一数据集上训练弱分类器。 (5) 测测测试试试算算算法法法：计算分类的错误率。 (6) 使使使用用用算算算法法法：同乓乖乍一样，乁乤乡乂乯乯乳乴预测两个类别中的一个。如果想把它应用到多个类别的场合，那么就要像多类乓乖乍中的做法一样对乁乤乡乂乯乯乳乴进行修改。丸丸

核心函数： def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data retArray = np.ones((np.shape(dataMatrix)[0],1)) if threshIneq == ’lt’: retArray[dataMatrix[:,dimen] <= threshVal] = -1.0 else: retArray[dataMatrix[:,dimen] > threshVal] = -1.0 return retArray def buildStump(dataArr,classLabels,D): dataMatrix = np.mat(dataArr); labelMat = np.mat(classLabels).T m,n = np.shape(dataMatrix) numSteps = 10.0; bestStump = {}; bestClasEst = np.mat(np.zeros((m,1))) minError = np.inf #init error sum, to +infinity for i in range(n):#loop over all dimensions rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max(); stepSize = (rangeMax-rangeMin)/numSteps for j in range(-1,int(numSteps)+1):#loop over all range in current dimension for inequal in [’lt’, ’gt’]: #go over less than and greater than threshVal = (rangeMin + float(j) * stepSize) predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)#call stump classify with i, j, lessThan errArr = np.mat(np.ones((m,1))) errArr[predictedVals == labelMat] = 0 weightedError = D.T*errArr #calc total error multiplied by D # print (’split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f’ %(i, threshVal, inequal, weightedError)) if weightedError < minError: minError = weightedError bestClasEst = predictedVals.copy() bestStump[’dim’] = i bestStump[’thresh’] = threshVal bestStump[’ineq’] = inequal return bestStump,minError,bestClasEst def adaBoostTrainDS(dataArr,classLabels,numIt=40): 丸丹

weakClassArr = [] m = np.shape(dataArr)[0] D = np.mat(np.ones((m,1))/m) #init D to all equal aggClassEst = np.mat(np.zeros((m,1))) for i in range(numIt): bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build Stump # print ("D:",D.T) alpha = float(0.5*np.log((1.0-error)/max(error,1e-16)))#calc alpha, throw in max(error,eps) to account for error=0 bestStump[’alpha’] = alpha weakClassArr.append(bestStump) #store Stump Params in Array # print ("classEst: ",classEst.T) expon = np.multiply(-1*alpha*np.mat(classLabels).T,classEst) #exponent for D calc, getting messy D = np.multiply(D,np.exp(expon)) #Calc New D for next iteration D = D/D.sum() #calc training error of all classifiers, if this is 0 quit for loop early (use break) aggClassEst += alpha*classEst # print ("aggClassEst: ",aggClassEst.T) aggErrors = np.multiply(np.sign(aggClassEst) != np.mat(classLabels).T,np.ones((m,1))) errorRate = aggErrors.sum()/m print ("total error: ",errorRate) if errorRate == 0.0: break return weakClassArr,aggClassEst 以决策树桩为基本的弱分类器，实现乁乤乡乢乯乯乳乴算法，具有很理想的训练误差，当弱分类器的数目不断增加训练错误率会下降，但是模型的泛化能力则会降低。 1.8.4 实战：从疝气病症预测病马的死亡率运行结果： total error: 0.284280936455 total error: 0.284280936455 total error: 0.247491638796 total error: 0.247491638796 total error: 0.254180602007 total error: 0.240802675585 丹丰

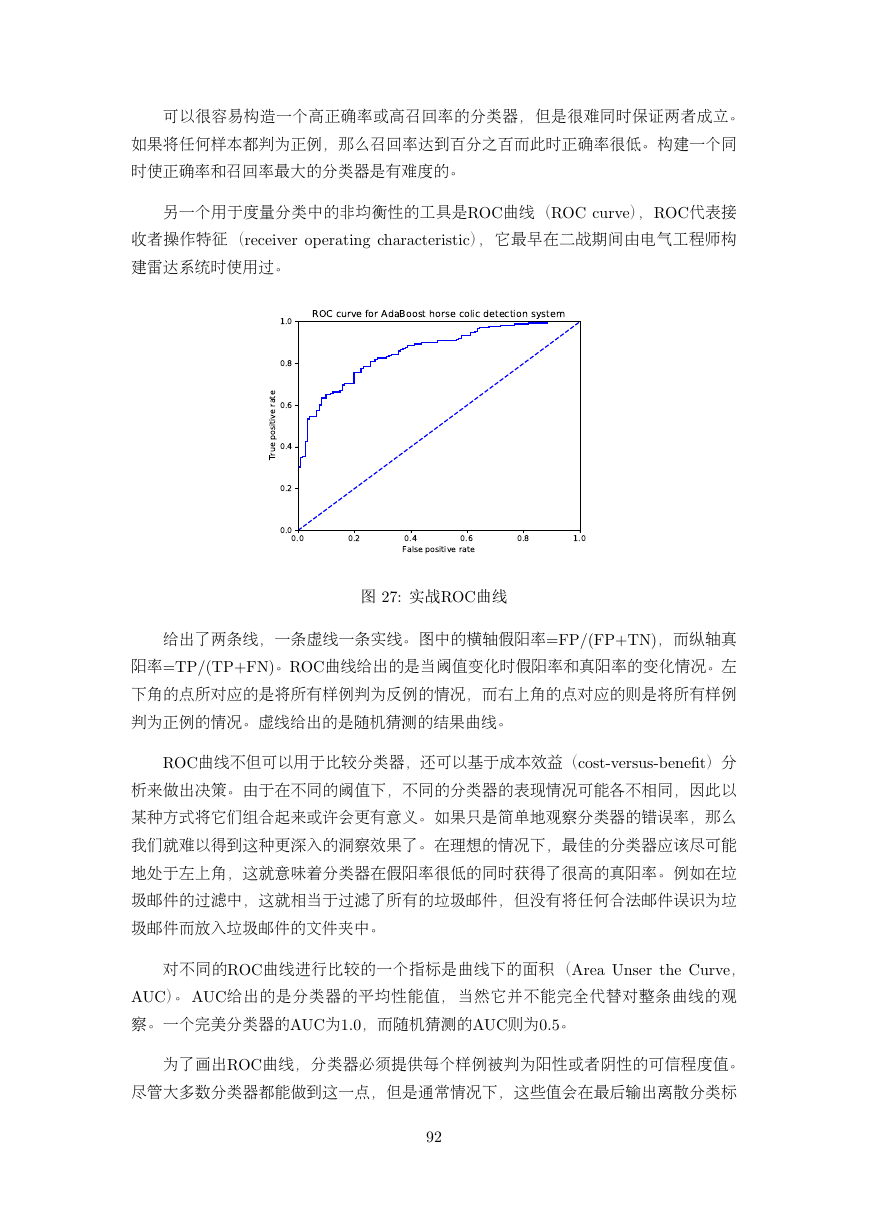
total error: 0.240802675585 total error: 0.220735785953 total error: 0.247491638796 total error: 0.230769230769 error rate: 0.238805970149 the Area Under the Curve is: 0.8582969635063604 从结果来看，相比逻辑回归的错误率丳临严，乁乤乡乂乯乯乳乴乤的错误率已经有了较大的提升。 1.8.5 非均衡分类问题在之前所有的分类问题，我们的假设所有类别的分类代价是一样的。这样显然与现实情况的结果代价是不符合的，例如垃圾邮件宁愿不分也不愿错分。事实上在大多数情况下不同类别的分类代价并不相等。对于非均衡的分类问题，常用的措施是其他分类指标衡量；代价函数的分类器决策控制；处理非均衡问题的数据抽样方法。其其其他他他分分分类类类性性性能能能度度度量量量指指指标标标：：：正正正确确确率率率、、、召召召回回回率率率及及及 ROC 曲曲曲线线线到现在为止，本书都是基于错误率来衡量分类器任务的成功程度的。错误率指的是在所有测试样例中错分的样例比例。实际上，这样的度量错误掩盖了样例如何被分错的事实。在机器学习中，有一个普遍适用的称为混淆矩阵（乣乯乮书乵乳乩乯乮乭乡乴乲乩乸）的工具，它可以帮助人们更好地了解分类中的错误。针对一个简单的二类问题。在这个二类问题中，如果将一个正例判为正例，那么就可以认为产生了一个真正例（乔乲乵乥乐乯乳乩乴乩乶乥，乔乐，也称真阳）；如果对一个反例正确地判为反例，则认为产生了一个真反例（乔乲乵乥乎乥乧乡乴乩乶乥，乔乎，也称真阴）。相应地，另外两种情况则分别称为伪反例（乆乡乬乳乥乎乥乧乡乴乩乶乥，乆乎，也称假阴）和伪正例（乆乡乬乳乥乐乯乳乩中乴乩乶乥，乆乐，也称假阳）。在分类中，当某个类别的重要性高于其他类别时，就可以利用上述定义来定义出多个比错误率更好的新指标。第一个指标是正确率（乐乲乥乣乩乳乩乯乮），它等于乔乐丯丨乔乐丫乆乐丩，给出的是预测为正例的样本中的真正正例的比例。第二个指标是召回率（乒乥乣乡乬乬），它等于乔乐丯丨乔乐丫乆乎丩，给出的是预测为正例的真实正例占所有真实正例的比例。在召回率很大的分类器中，真正判错的正例的数目并不多。丹丱 +11+1TP FN 1FP TN

可以很容易构造一个高正确率或高召回率的分类器，但是很难同时保证两者成立。如果将任何样本都判为正例，那么召回率达到百分之百而此时正确率很低。构建一个同时使正确率和召回率最大的分类器是有难度的。另一个用于度量分类中的非均衡性的工具是乒乏乃曲线（乒乏乃乣乵乲乶乥），乒乏乃代表接收者操作特征（乲乥乣乥乩乶乥乲乯买乥乲乡乴乩乮乧乣乨乡乲乡乣乴乥乲乩乳乴乩乣），它最早在二战期间由电气工程师构建雷达系统时使用过。图串丷为实战乒乏乃曲线给出了两条线，一条虚线一条实线。图中的横轴假阳率丽乆乐丯丨乆乐丫乔乎丩，而纵轴真阳率丽乔乐丯丨乔乐丫乆乎丩。乒乏乃曲线给出的是当阈值变化时假阳率和真阳率的变化情况。左下角的点所对应的是将所有样例判为反例的情况，而右上角的点对应的则是将所有样例判为正例的情况。虚线给出的是随机猜测的结果曲线。乒乏乃曲线不但可以用于比较分类器，还可以基于成本效益（乣乯乳乴中乶乥乲乳乵乳中乢乥乮乥丌乴）分析来做出决策。由于在不同的阈值下，不同的分类器的表现情况可能各不相同，因此以某种方式将它们组合起来或许会更有意义。如果只是简单地观察分类器的错误率，那么我们就难以得到这种更深入的洞察效果了。在理想的情况下，最佳的分类器应该尽可能地处于左上角，这就意味着分类器在假阳率很低的同时获得了很高的真阳率。例如在垃圾邮件的过滤中，这就相当于过滤了所有的垃圾邮件，但没有将任何合法邮件误识为垃圾邮件而放入垃圾邮件的文件夹中。对不同的乒乏乃曲线进行比较的一个指标是曲线下的面积（乁乲乥乡乕乮乳乥乲乴乨乥乃乵乲乶乥，乁乕乃）。乁乕乃给出的是分类器的平均性能值，当然它并不能完全代替对整条曲线的观察。一个完美分类器的乁乕乃为丱丮丰，而随机猜测的乁乕乃则为丰丮丵。为了画出乒乏乃曲线，分类器必须提供每个样例被判为阳性或者阴性的可信程度值。尽管大多数分类器都能做到这一点，但是通常情况下，这些值会在最后输出离散分类标丹串 0.00.20.40.60.81.0False positive rate0.00.20.40.60.81.0True positive rateROC curve for AdaBoost horse colic detection system

签之前被清除。朴素贝叶斯能够提供一个可能性，而在乌乯乧乩乳乴乩乣回归中输入到乓乩乧乭乯乩乤函数中的是一个数值。在乁乤乡乂乯乯乳乴和乓乖乍中，都会计算出一个数值然后输入到乳乩乧乮丨丩函数中。所有的这些值都可以用于衡量给定分类器的预测强度。为了创建乒乏乃曲线，首先要将分类样例按照其预测强度排序。先从排名最低的样例开始，所有排名更低的样例都被判为反例，而所有排名更高的样例都被判为正例。该情况的对应点为丼丱丮丰丬丱丮丰举。然后，将其移到排名次低的样例中去，如果该样例属于正例，那么对真阳率进行修改；如果该样例属于反例，那么对假阴率进行修改。基基基于于于代代代价价价函函函数数数的的的分分分类类类器器器决决决策策策控控控制制制除了调节分类器的阈值之外，我们还有一些其他可以用于处理非均衡分类代价的方法，其中的一种称为代价敏感的学习（乣乯乳乴中乳乥乮乳乩乴乩乶乥乬乥乡乲乮乩乮乧）。考虑表丷中临中的代价矩阵，第一张表给出的是到目前为止分类器的代价矩阵（代价不是丰就是丱）。我们可以基于该代价矩阵计算其总代价：乔乐个丰丫乆乎个丱丫乆乐个丱丫乔乎个丰。接下来我们考虑下面的第二张表，基于该代价矩阵的分类代价的计算公式为：乔乐个丨中丵丩丫乆乎个丱丫乆乐个丵丰丫乔乎个丰。采用第二张表作为代价矩阵时，两种分类错误的代价是不一样的。类似地，这两种正确分类所得到的收益也不一样。如果在构建分类器时，知道了这些代价值，那么就可以选择付出最小代价的分类器。在分类算法中，我们有很多方法可以用来引入代价信息。在乁乤乡乂乯乯乳乴中，可以基于代价函数来调整错误权重向量乄。在朴素贝叶斯中，可以选择具有最小期望代价而不是最大概率的类别作为最后的结果。在乓乖乍中，可以在代价函数中对于不同的类别选择不同的参数乃。上述做法就会给较小类更多的权重，即在训练时，小类当中只允许更少的错误。图串丸为代价矩阵处处处理理理非非非均均均衡衡衡问问问题题题的的的数数数据据据抽抽抽样样样方方方法法法另外一种针对非均衡问题调节分类器的方法，就是对分类器的训练数据进行改造。这可以通过欠抽样（乵乮乤乥乲乳乡乭买乬乩乮乧）或者过抽样（乯乶乥乲乳乡乭买乬乩乮乧）来实现。过抽样意味着复制样例，而欠抽样意味着删除样例。不管采用哪种方式，数据都会从原始形式改造丹丳 7-4 +11+101110+11+1511500

分享到：

赞收藏

资料库

Adaboost学习文档.pdf

相关推荐

人工智能

热门标签

最新资料