哈工大算法实验.docx

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：0.09M 资料格式：docx 举报版权申诉

qq_29776675-9327401-4744302542931351848.docx.pdf-第1页.png

第1页 / 共17页

qq_29776675-9327401-4744302542931351848.docx.pdf-第2页.png

第2页 / 共17页

qq_29776675-9327401-4744302542931351848.docx.pdf-第3页.png

第3页 / 共17页

qq_29776675-9327401-4744302542931351848.docx.pdf-第4页.png

第4页 / 共17页

qq_29776675-9327401-4744302542931351848.docx.pdf-第5页.png

第5页 / 共17页

qq_29776675-9327401-4744302542931351848.docx.pdf-第6页.png

第6页 / 共17页

qq_29776675-9327401-4744302542931351848.docx.pdf-第7页.png

第7页 / 共17页

qq_29776675-9327401-4744302542931351848.docx.pdf-第8页.png

第8页 / 共17页

判断点线关系及计算多边形内角

一、点与线的关系

二、计算多边形内角

凸包生成算法

一、凸包定义

二、Graham算法思想

三、编程实现

实验报告班级：学生姓名：学日号： 201101218 期: 2014 年 5 月 11 日

判断点线关系及计算多边形内角一、点与线的关系（1）定义：平面上的三点 P1(x1,y1),P2(x2,y2),P3(x3,y3)的面积量： |x1 x2 x3| S(P1,P2,P3) = |y1 y2 y3| = (x1-x3)*(y2-y3) - (y1-y3)*(x2-x3) |1 1 1 | 当 P1P2P3 逆时针时 S 为正的，当 P1P2P3 顺时针时 S 为负的。令矢量的起点为 A，终点为 B，判断的点为 C，如果 S（A，B，C）为正数，则 C 在矢量 AB 的左侧；如果 S（A，B，C）为负数，则 C 在矢量 AB 的右侧；如果 S（A，B，C）为 0，则 C 在直线 AB 上。（2）算法 int MyMath::IsRightInLine(MyPoint p1, MyPoint p2, MyPoint p3) { int s; s = (p1.x-p3.x)*(p2.y-p3.y)-(p1.y-p3.y)*(p2.x-p3.x); if (s>0) { return 1; //点在直线左侧 } else if (s<0) { return 2;//点在直线右侧 } else { } } return 0;//点在直线上二、计算多边形内角（1）算法过程第一步：输入一系列的离散点；

第二步：找 x 坐标值最小的点 p0，这样能确定由此点构成的多边形的角是凸的；第三步：定义与 p0 点相邻的前后两个点 p1，p2，若超出数组边界，则用首点或尾点取代；第四步：计算 p2 与向量 p1p0 的位置关系，若 p2 在向量 p1p0 的左边，则多边形呈逆时针方向；若 p2 在向量 p1p0 的右边，则多边形呈顺时针方向。第五步：计算多边形的各个内角，利用两个向量的夹角公式计算。由于多边形有凹凸性，所以算角时要分情况。找规律可知，若多边形是逆时针走向，那么，若三个相邻的点构成凸角，三点的走向始终是逆时针走向，否则，是顺时针走向，故可根据此来确定角度。（2）算法实现 1、定义点类 class MyPoint { public: MyPoint(); virtual ~MyPoint(); public: int id; int x,y,z; }; 2、定义数学计算类 class MyMath { public: MyMath(); virtual ~MyMath(); public: static float CalcuAngle(MyPoint p1,MyPoint p2,MyPoint p3,int flag);//算角度 static int IsRightInLine(MyPoint p1,MyPoint p2,MyPoint p3);//判断点与直线位置关系 protected: static static }; float VectorAngel(MyPoint p1,MyPoint p2,MyPoint p3);//计算向量角 float CalCuMatrix(MyPoint p1,MyPoint p2,MyPoint p3); 详细代码： //点与直线的关系 int MyMath::IsRightInLine(MyPoint p1, MyPoint p2, MyPoint p3) { int s; s = (p1.x-p3.x)*(p2.y-p3.y)-(p1.y-p3.y)*(p2.x-p3.x);

if (s>0) { return 1; //点在直线左侧 } else if (s<0) { return 2;//点在直线右侧 } else { } return 0;//点在直线上 } //计算角度 float MyMath::CalcuAngle(MyPoint p1, MyPoint p2, MyPoint p3,int flag) { //判断正逆方向 float d = CalCuMatrix(p1,p2,p3); float angle = VectorAngel(p1,p2,p3); if (flag==1) { if (d>0)//逆时针，凸多边形(在数学坐标系中正确，程序中相反) { return (180.0-angle); } else //顺时针，凹多边形 { return (180.0+angle); } } if (flag==2) { if (d>0)//逆时针，凸多边形 { return (180.0+angle); } else //顺时针，凹多边形 { return (180.0-angle); } } }

//求矩阵，用于判断走向 float MyMath::CalCuMatrix(MyPoint p1,MyPoint p2,MyPoint p3) { return ((p1.x*p2.y+p1.y*p3.x+p2.x*p3.y)-(p2.y*p3.x+p3.y*p1.x+p1.y*p2.x)); } //求向量夹角 float MyMath::VectorAngel(MyPoint p1, MyPoint p2, MyPoint p3) { int dx1 = p2.x-p1.x; int dy1 = p2.y-p1.y; int dx2 = p3.x-p2.x; int dy2 = p3.y-p2.y; float a = (dx1*dx2+dy1*dy2)/(sqrt(dx1*dx1+dy1*dy1)*sqrt(dx2*dx2+dy2*dy2)); return (180*acos(a))/3.1415; } 3、定义多边形类 class MyPolygon { public: MyPolygon(); virtual ~MyPolygon(); public: CArray dingDianArray;//多边形顶点 CArray trangleArray; int flag;//判断顺逆方向,逆为 2，顺为 1，初始为 0 //角度 public: void AddPoint(MyPoint p);//加点 void DrawPolygon(CDC * pDC);//画多边形 bool Cacul();//计算夹角 }；详细代码： //画多边形 void MyPolygon::DrawPolygon(CDC * pDC) { CPen *pen = new CPen(0, 1, RGB(255,0,0)); CPen* oldPen = pDC->SelectObject(pen); int ix,iy; int dianCount=dingDianArray.GetSize(); //画点 for (int i=0;i

ix = dingDianArray[i].x; iy = dingDianArray[i].y; pDC->Ellipse(ix-3,iy-3,ix+3,iy+3); } //画边 if (dianCount>=3) { pDC->MoveTo(dingDianArray[0].x,dingDianArray[0].y); for(int i=1;iLineTo(dingDianArray[i].x,dingDianArray[i].y); } pDC->LineTo(dingDianArray[0].x,dingDianArray[0].y); } //画角度 if (trangleArray.GetSize()>0) { for (int i=0;iTextOut(dingDianArray[i].x,dingDianArray[i].y,s); } } pDC->SelectObject(oldPen); } //加点 void MyPolygon::AddPoint(MyPoint p) { dingDianArray.Add(p); } //计算方向和角度 bool MyPolygon::Cacul() { if (dingDianArray.GetSize()<3) { flag = 0; return false; } else {

//找 x 值最小的点 int index=0; MyPoint p = dingDianArray[0]; for (int i=1;ipi.x) { index= i; p = pi; } } //定义与当前点相邻的两点 int i_1 = index -1; int i1 = index+1; if (i_1<0) { i_1 = dingDianArray.GetSize ()-1; } if (i1>dingDianArray.GetSize()-1) { i1=0; } MyPoint pi_1 = dingDianArray[i_1]; MyPoint pi1 = dingDianArray[i1]; //判断点线位置关系，确定多边形的走向 int isRight = MyMath::IsRightInLine(pi_1,p,pi1); if (isRight==1) { flag = 1; } else if (isRight==2) { flag = 2; } else { flag=0; } //计算多边形内角 trangleArray.RemoveAll(); for( i=0;i

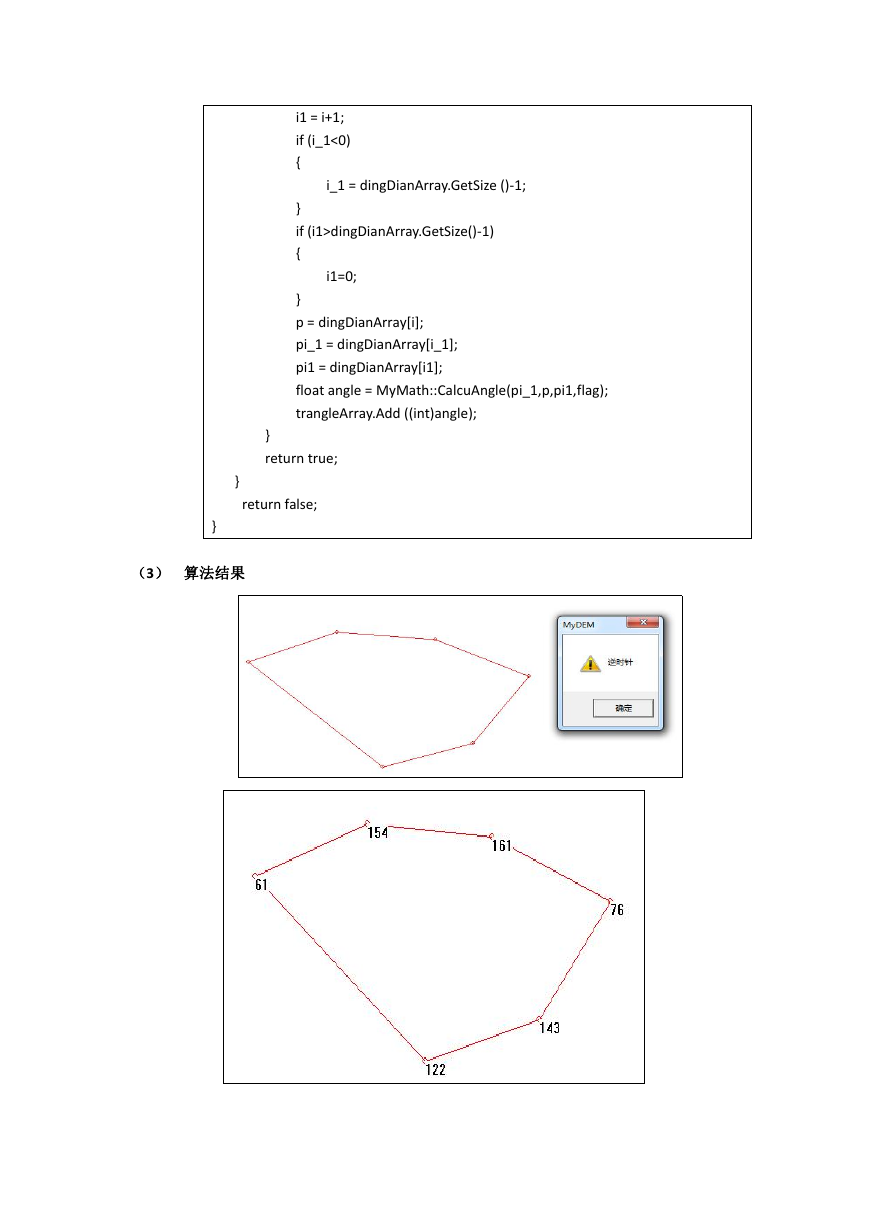
i1 = i+1; if (i_1<0) { i_1 = dingDianArray.GetSize ()-1; } if (i1>dingDianArray.GetSize()-1) { i1=0; } p = dingDianArray[i]; pi_1 = dingDianArray[i_1]; pi1 = dingDianArray[i1]; float angle = MyMath::CalcuAngle(pi_1,p,pi1,flag); trangleArray.Add ((int)angle); } return true; } } return false; （3）算法结果

分享到：

赞收藏

资料库

哈工大算法实验.docx

相关推荐

课程资源

热门标签

最新资料