logo资料库

三机九节点的暂态稳定性分析.docx

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.14M 资料格式：docx 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    暂态稳定分析仿真 考虑如图 2 所示的 9 节点电力系统。该系统有三台发电机、3 个负荷以及 9 条支路。支路数据和发电机参数分别列于表 1 和表 2，系统频率为 60Hz。干扰是 在零秒线路 5—7 靠近母线 7 处发生三相短路，故障在 5 个周波（约 0.08333） 由断开线路 5—7 而被消除。 2 3 2 7 8 9 3 5 6 4 1 1 图 2 表 1 支路数据 首端母线名 末端母线名 电阻(标幺 电抗(标幺 容纳之半(标 变压器非标 值) 0.010 0.017 0.032 0.039 0.0085 0.0119 0 0 0 值) 0.085 0.092 0.161 0.170 0.072 0.1008 0.0576 0.0625 0.0586 幺值) 0.088 0.079 0.153 0.179 0.0745 0.1045 准变比 1.0 1.0 1.0 5 6 7 9 8 9 4 7 9 4 4 5 6 7 8 1 2 3 发电 母线 JT aR dX 'dX qX 'qX 0'dT 0'qT D 表 2 发电机数据
    机 名 1 2 3 1 2 3 47.28 12.80 6.02 0 0 0 0.1460 0.0608 0.0969 0.0969 0.8958 0.1198 0.8645 0.1969 1.3125 0.1813 1.2578 0.2500 8.96 6.00 8.59 0.535 0.600 0 0 0 2.1 初值计算结果 利用 Matlab 进行潮流计算得到系统正常运行情况下的参数，运行结果如下 所示： 整理可得到表 3： 表 3 正常运行情况下的系统潮流 母线名 电压 发电机 负荷 幅值 相角 有功功率 无功功率 有功功率 无功功率 0.7164 1.6300 0.8500 0.2705 0.0665 -0.1086 1 2 3 4 5 6 7 1.0400 1.0250 1.0250 1.0258 0.9956 1.0127 1.0258 0 9.2800 4.6647 -2.2168 -3.9888 -3.6874 3.7197 1.2500 0.9000 0.5000 0.3000
    8 9 1.0159 1.0324 0.7275 1.9667 1.0000 0.3500 各发电机的暂态电动势，功角和输入机械功率初值计算结果如下： 计凸极效应： 不计凸极效应（令 X q X ）： ' d 整理得到表 4： 表 4 发电机的 ' q E 、 及P (0) (0) m 发电机 不计凸极效应 计凸极效应 ' qE 1.0566 1.0502 1.0170 (0) 2.2716 19.7316 13.1664 ' qE 1.0564 0.7882 0.7679 (0) 3.5857 61.0984 54.1366 1 2 3 mP (0) 0.7164 1.6300 0.8500 各节点的等值导纳计算结果如下：
    即，负荷（节点 5）：1.2610—j0.5044 负荷（节点 6）：0.8776—j0.2925 负荷（节点 8）：0.9690—j0.3391 2.2 故障系统和故障后系统描述 故障期间的电网络相当于在 7 号母线处并联一条阻抗为零的接地支路，这时 只要将正常情况下导纳矩阵Y 中的对角元素 77Y 改为无穷大（实际计算中取 2010 ）， 即可得到故障期间系统的节点导纳矩阵。 故障后的电网络是切除线路 5—7 后的情况，由于线路 5—7 对导纳的贡献为： Y l (5 7)      5     7        1  r  jx  1   r    jx 5 7    jb   r  1   jx  jb 1  r jx                式中： 0.032,  r x  0.161, b  0.153 Y ，因此故障后导纳矩阵为： P   Y Y  (5 7) l 。 2.3 相对摇摆角计算结果 根据系统的初值，利用 Matlab 求解网络方程和微分方程得到相对摇摆角计 算结果如图 3 和图 4 所示。
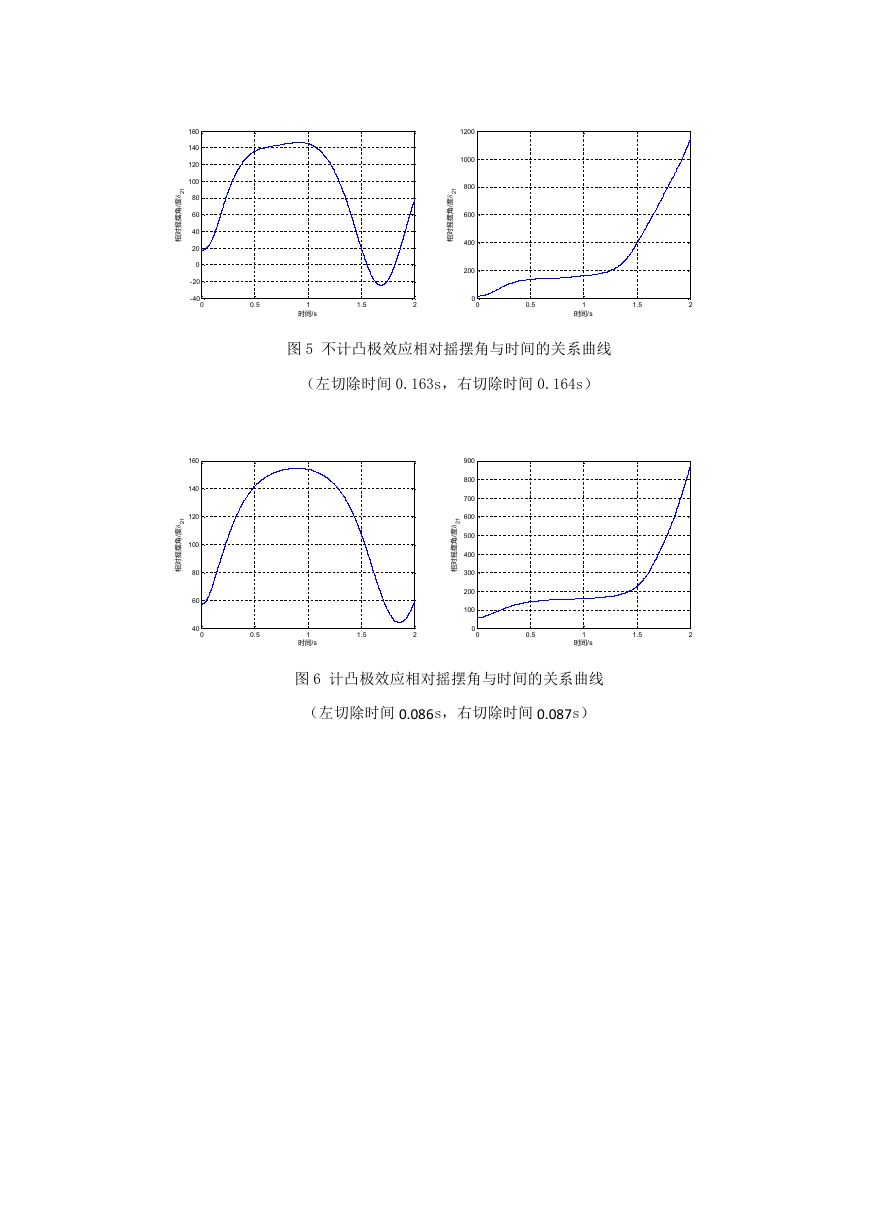
    160 140 120 1 2 /  度 角 摆 摇 对 相 100 80 60 40 0 90 80 70 60 50 40 30 20 10 1 2 /  度 角 摆 摇 对 相 0.5 1 时间/s 1.5 2 图 3 计凸极效应 0 0 0.5 1 时间/s 1.5 2 图 4 不计凸极效应 由图 3 和图 4 可以看出，无论计凸极效应还是不计凸极效应，系统都是暂态 稳定的。在计凸极效应的情况下，最大相对摇摆角为 149.8768 度。在不计凸极 效应的情况下，最大相对摇摆角为 85.3312 度，而第二摆的角度 85.1118 度比第 一摆的角度小。 最后，对不计凸极效应和计凸极效应情况下的临界切除时间进行仿真模拟。 得到前者所对应的临界切除时间在 0.163s—0.164s 之间，后者所对应的临界切 除时间在 0.086s—0.087s 之间。它们对应的摇摆曲线分别如图 5 和图 6。
    1 2 /  度 角 摆 摇 对 相 160 140 120 100 80 60 40 20 0 -20 -40 0 160 140 120 1 2 /  度 角 摆 摇 对 相 100 80 60 40 0 1200 1000 800 1 2 /  度 角 摆 摇 对 相 600 400 200 0 0 0.5 1 时间/s 1.5 2 0.5 1 时间/s 1.5 2 图 5 不计凸极效应相对摇摆角与时间的关系曲线 （左切除时间 0.163s，右切除时间 0.164s） 900 800 700 600 1 2 /  度 角 摆 摇 对 相 500 400 300 200 100 0 0 0.5 1 时间/s 1.5 2 0.5 1 时间/s 1.5 2 图 6 计凸极效应相对摇摆角与时间的关系曲线 （左切除时间 0.086s，右切除时间 0.087s）
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料