logo资料库

基于人工神经网络的模式识别论文及源程序.doc

发布时间：2022-06-10 发布人：admin 分类：说明书 资料大小：0.56M 资料格式：doc 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    基于人工神经网络的模式识别 摘要：人工神经网络发展越来越快，已经为科研、生产、生活所普遍应用。 本文主要研究并设计一个能够识别含有噪声的英文字母的人工神经网络。 关键字：神经网络；模式识别；设计；MATLAB 1． 研究背景及问题的阐述 1.1 研究背景[1] 人工神经网络是近年来研究的热点,其多应用于建模、时间序列分析、模式 识别和控制等领域。它的理论与实践有引人注目的进展, 再一次拓展了计算概念 的内涵, 使神经计算、进化计算成为新的学科。神经网络也有助于机器进行模式 识别。这是一个非常有实用价值的例子：在规定的格子里填上表明地区区号的编 码．信封到了邮局后，通过一定的处理程序，就能够自动地用机器而不是人识别 其号码，并根据号码内容将其放到合适的位置而达到分类的目的。在这入分信封 的过程中，起关键性的数字辨识功能就可以用神经网络来完成。不过神经网络自 身仅能够处理数据，所以对于需要神经网络完成的任务，都必须首先将其转化成 神经网络所能够接收的输入和输出数据．即使对邮政编码辨识这样一个不复杂的 任务，也必须先对信封编码部位进行扫描，并对图像进行预处理，将含有数字的 部分用点阵画出其图形，产生一定数目的比如用 0 和 1 数字表示的数字符号的数 组后，才能将其送人神经网络的输人端进行辨识。实际上，任何一个实际应用问 题，都有一个将其转化成神经网络所能够接受的数据的转化问题，这种转化往往 并不是一件容易的事。 1.2 问题的描述 设计训练一个神经网络能够识别 26 个英文字母，意味着当给训练过的网络 一个表示某一字母的输人时，网络能够正确地在输出端指出该字母，那么很显然， 该网络记住了所有 26 个字母。神经网络的训练应当是有监督地训练出输人端的 26 组分别表示字母 A 到 Z 的数组，能够对应出输出端 1 到 26 的具休的位 置．首先必须将每个字母进行数字化处理，以便构造输人样本。考虑用 5 ×7 矩 阵的布尔值可以清楚地表示出每个字母，例如字母 A 和 Z 分别可以用 0 、 l 矩阵表示为： 1
    Letter A=[0 0 1 0 0， 0 1 0 1 0， 0 1 0 1 0， 1 0 0 0 1 ， 1 1 1 1 1 ， 1 0 0 0 1 ， 1 0 0 01 ]T Letter Z=[1 1 1 11 ， 0 0 0 0 1 ， 0 0 0 1 0 ， 0 0 1 0 0 ， 0 1 0 0 0 ， 1 0 0 0 0， 1 1 1 1 1 ]T 每个字母都可以用此 5×7 =35 的元素组成一个字母的列矩阵，那么由表示 26 个字母的输人的列矩阵组成的 26×35 的输人矩阵。然后把这 26 个字母送入 变量名为 aiphabet 中： alphabet=[letter A, letter B, letter C, letter D, letter E, letter F, letter G, letter H…letter I, letterJ, letter K, letter L, letter M, letter N, letter O, letter P, letter Q, letter R…letter S, letter T, letter U, letter V, letter W, letter X, letter Y, letter Z] 字母表如图 1.1 图 1.1 用 5×7 的矩阵表示的字母 A 和 Z 另外一个很重要的需要考虑的因素是：所要设计的网络应当具有抗干扰能 力，即设计出的网络应当能够处理噪声。具有在由一定不规范的输人情况下辨识 2
    出正确的字母输人的能力。将干扰噪声进行数字化处理后即变成具有平均值为 0-0.2 之间变化的随机值。 2． 神经网络的设计 2.1 网络结构 所设计的神经网络需要具有 35 个输人节点和 26 个输出神经元。采用输人 在（0，1）范围的对数 S 型激活函数两层 logsin/logsin 网络，这种网络对 0-1 型 布尔值是相当完美的．网络取 35-8-26 的结构．隐含层凭经验取 10 个神经元， 如果需要网络有更高的辨识精度，可以再增加一些隐含层神经元数，在本例中， 其辨识训练精度对于无噪声的 err_goal 取为 0.1；对于带有噪声的辨识目标误差 只要求为 0.6，此目标均在 5000 次训练内达到。网络的设计是为了使其输出矢量 在正确的位置上输出为 1，而在其他位置上输出为 0, 然而，噪声输人矢量可能 导致网络的 1 或 0 输出不正确，或出现其他输出值。所以为了使网络具有抗干 扰能力，在网络训练后，再将其经过一层竞争网络函数 compet.m 的处理再输出。 使网络的输出只在最接近输人值的输出位置输出为 1，保证在其他位置输出均为 0。 2.2 初始化 本文仅以 A 和 Z 为例； alphabet=[0 0 1 0 0,0 1 0 1 0,0 1 0 1 0,1 0 0 0 1 ,1 1 1 1 1,1 0 0 0 1 ,1 0 0 0 1;1 1 1 1 1,0 0 0 0 1,0 0 0 1 0,0 0 1 0 0,0 1 0 0 0,1 0 0 0 0,1 1 1 1 1 ]'; targets=[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]'; net=newff(minmax(alphabet),[8,26],{'logsig','purelin'},'t raingda'); 2.3 网络训练 为了使网络对输入向量有一定的容错能力, 最好的办法是既使用理想的信 号又使用带有噪声的信号对网络进行训练。具体做法是先用理想的输入信号对网 络进行训练, 直到其平方和误差足够小。接下来, 使用 10 组理想信号和带有噪 声的信号对网络进行训练。在输入带有误差的向量时, 要输入两倍重复的无误差 信号, 这样做的目的是为了保证网络在分辨理想输入向量时的稳定性。在网络进 3
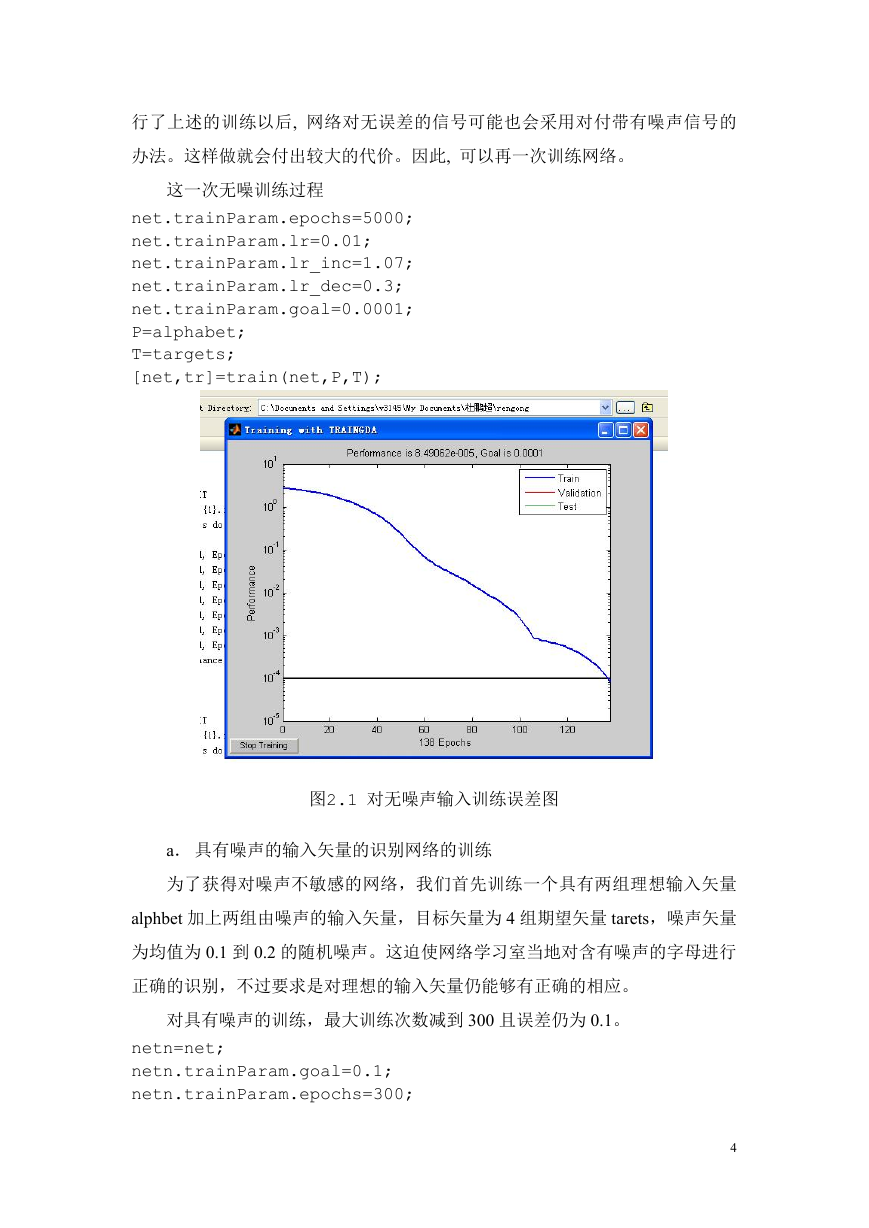
    行了上述的训练以后, 网络对无误差的信号可能也会采用对付带有噪声信号的 办法。这样做就会付出较大的代价。因此, 可以再一次训练网络。 这一次无噪训练过程 net.trainParam.epochs=5000; net.trainParam.lr=0.01; net.trainParam.lr_inc=1.07; net.trainParam.lr_dec=0.3; net.trainParam.goal=0.0001; P=alphabet; T=targets; [net,tr]=train(net,P,T); 图2.1 对无噪声输入训练误差图 a． 具有噪声的输入矢量的识别网络的训练 为了获得对噪声不敏感的网络，我们首先训练一个具有两组理想输入矢量 alphbet 加上两组由噪声的输入矢量，目标矢量为 4 组期望矢量 tarets，噪声矢量 为均值为 0.1 到 0.2 的随机噪声。这迫使网络学习室当地对含有噪声的字母进行 正确的识别，不过要求是对理想的输入矢量仍能够有正确的相应。 对具有噪声的训练，最大训练次数减到 300 且误差仍为 0.1。 netn=net; netn.trainParam.goal=0.1; netn.trainParam.epochs=300; 4
    for pass=1:10 T=[targets targets targets targets]; P=[alphabet,alphabet,(alphabet+randn(R,Q)*0.1), (alphabet+randn(R,Q)*0.2)]; [netn,tr]=train(netn,P,T); End 图2.2 对有噪声输入训练误差图 图2.3 对有噪声输入训练误差图 5
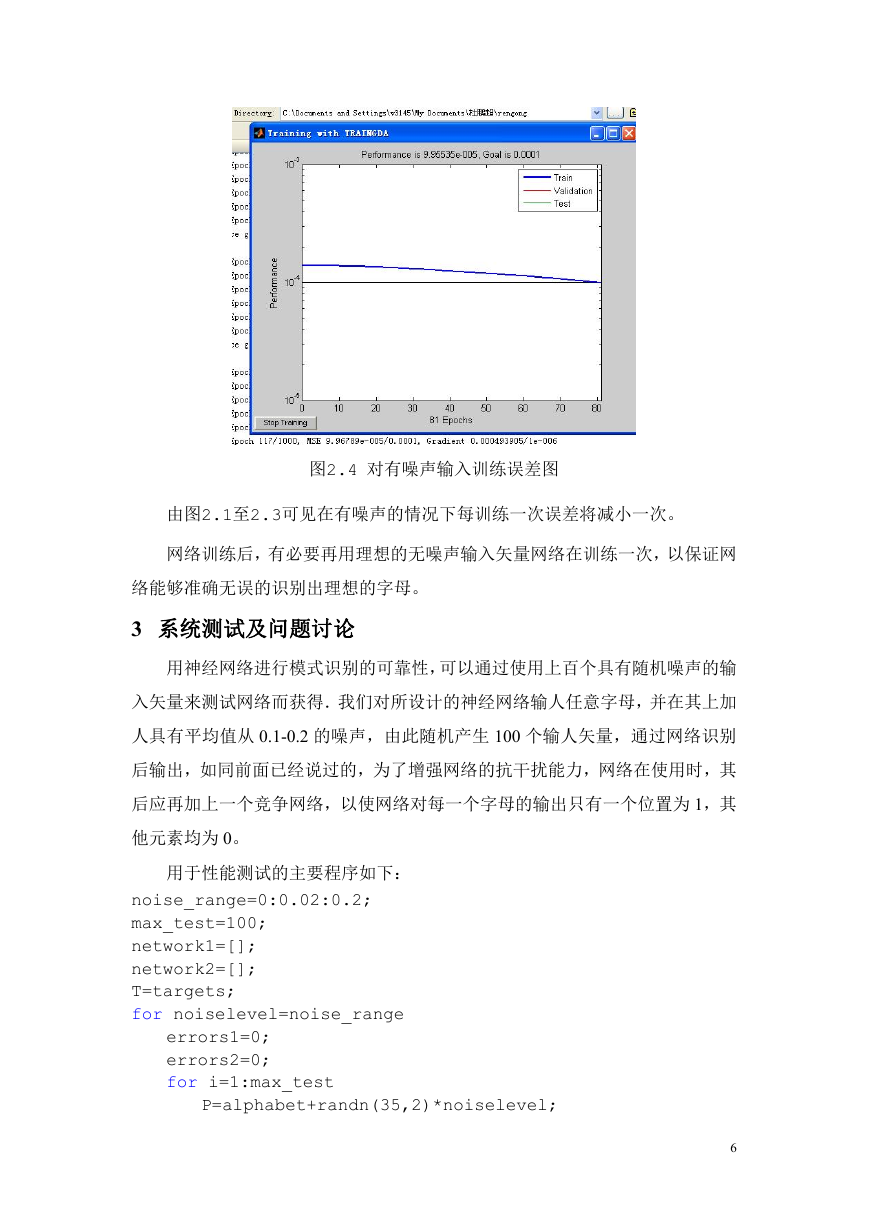
    图2.4 对有噪声输入训练误差图 由图2.1至2.3可见在有噪声的情况下每训练一次误差将减小一次。 网络训练后，有必要再用理想的无噪声输入矢量网络在训练一次，以保证网 络能够准确无误的识别出理想的字母。 3 系统测试及问题讨论 用神经网络进行模式识别的可靠性，可以通过使用上百个具有随机噪声的输 入矢量来测试网络而获得．我们对所设计的神经网络输人任意字母，并在其上加 人具有平均值从 0.1-0.2 的噪声，由此随机产生 100 个输人矢量，通过网络识别 后输出，如同前面已经说过的，为了增强网络的抗干扰能力，网络在使用时，其 后应再加上一个竞争网络，以使网络对每一个字母的输出只有一个位置为 1，其 他元素均为 0。 用于性能测试的主要程序如下： noise_range=0:0.02:0.2; max_test=100; network1=[]; network2=[]; T=targets; for noiselevel=noise_range errors1=0; errors2=0; for i=1:max_test P=alphabet+randn(35,2)*noiselevel; 6
    A=sim(net,P); AA=compet(A); errors1=errors1+sum(sum(abs(AA-T)))/2; An=sim(netn,P); AAn=compet(An); errors2=errors2+sum(sum(abs(AAn-T)))/2; end network1=[network1,errors1/26/100]; network2=[network2,errors2/26/100]; end figure(1); plot(noise_range,network1*100,'r-',noise_range,network2*1 00,'b-'); xlabel('noise level'); ylabel('percentage of recognition'); 图2.4 无噪声训练网络与有噪声网络误差对比 由程序可以看出，测试结束后，绘制了辨识的出错百分比。为了对比起见， 我们在测试同时加进了对用无噪声的理想字母训练的字母辨识神经网络的测试， 并也画出了用其辨识字母的出错率，测试和作图程序与带噪声的上述程序完全相 同。两者的比较如图 2.4 所示，图中红线代表用无噪声训练的网络的辨识出错率。 蓝线为带有噪音训练出的网络情况。由图中可见，两网络都有一定的抗干扰能力， 7
    在平均值为 0-0.4 之间的噪声的影响，都能够几乎 100%地准确无误的辨识出， 而在较大的噪声出现后，比如 0.14-0.2 之间，理想网络明显比带噪声训练网络的 出错率要高出许多，在平均噪声为 0.2 的情况下，带噪声的网络的出错率仅为几 乎没有，而它的对比结果却达到 0.45%。 4 结论 在本文中讨论了设计一个简单的模式识别系统的设计方案。需要引起注意的 是: 训练过程不只是包含一个训练函数,它还需要用不同的输入向量进行很多次 训练。如果需要有更高的精度, 一种办法是增长网络的训练时间, 另一种办法是 增加网络隐含层的神经元数目。当然, 把输入的字母表向量从 5×7 的网络增加 到 10×14 的网格也是一种办法。另外, 如果网络要求对误差信号有更高的可靠 性, 还可以在训练时增加输入向量的误差的数量。在本文中, 使用了不同的噪声 向量作为输入来训练网络, 使得网络具有了容错的能力, 这样更适合在现实环境 中使用。 整体来讲，用人工神经网络进行的模式识别能够很好的完成识别功能。 参考文献： [1] 但小容.王瑞.杨莉, 基于人工神经网络的模式识别, 软件导刊,2007 [2] 丛爽.面向 MATLAB 工具箱的神经网络理论与应用[M] .合肥:中国科学技术 大学出版社,1998. 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    网络技术

    共收录2367份资料，累计7个分类，关注成员有19位，主要包括：综合布线,网管软件,网络监控,网络设备,其它,系统集成,网络基础

    热门标签

    综合布线 网管软件 网络监控 网络设备 其它 系统集成 网络基础

    最新资料