logo资料库

时间序列的复杂度和熵.pdf

发布时间：2022-06-01 发布人：admin 分类：说明书 资料大小：0.45M 资料格式：pdf 举报 版权申诉
第1页 / 共20页
第2页 / 共20页
第3页 / 共20页
第4页 / 共20页
第5页 / 共20页
第6页 / 共20页
第7页 / 共20页
第8页 / 共20页
资料共20页，剩余部分请下载后查看
    6 时间序列的复杂度和熵
    6.1 引言
    6.2 时间序列符号化方法
    6.3 热力学熵－克劳修斯(Clausius)熵[5, 6]
    6.4 统计熵－玻尔兹曼(Boltzmann)熵[5]
    6.5 信息熵－先农(Shannon)熵[5, 7]
    6.6 Kolmogrov熵和K2熵
    6.7 非广延熵-Tsallis熵
    6.8 近似熵－Approximate Entropy
    6.9 样本熵－Sample Entropy
    6.10 多尺度熵－Multiscale Entropy
    6.11 Lempel-Ziv复杂度
    6.12 相似指数分析[24]
    6.13 海杂波的复杂度和熵
    6.14 本章小结
    6.15 后记
    6 时间序列的复杂度和熵 6 时间序列的复杂度和熵 ............................................................................................ 1 6.1 引言............................................................................................................................. 2 6.2 时间序列符号化方法................................................................................................. 2 6.3 热力学熵－克劳修斯(Clausius)熵[5, 6] ...................................................................... 4 6.4 统计熵－玻尔兹曼(Boltzmann)熵[5] ......................................................................... 6 6.5 信息熵－先农(Shannon)熵[5, 7] .................................................................................. 6 6.6 Kolmogrov熵和K2 熵 ................................................................................................ 8 6.7 非广延熵-Tsallis熵..................................................................................................... 9 6.8 近似熵－Approximate Entropy................................................................................ 10 6.9 样本熵－Sample Entropy......................................................................................... 12 6.10 多尺度熵－Multiscale Entropy................................................................................ 14 6.11 Lempel-Ziv复杂度 ................................................................................................... 16 6.12 相似指数分析[24] ...................................................................................................... 17 6.13 海杂波的复杂度和熵............................................................................................... 18 6.14 本章小结................................................................................................................... 18 6.15 后记........................................................................................................................... 19 -1 -
    6.1 引言 在对动力学结构进行动力学特性分析时，首先对结构进行非线性检测，并判断该系 统的非线性因素是否可以忽略非常重要。一个系统的熵和复杂度隐含着整个系统运动规 律,他们的物理意义直接和系统单一变量的性质相联系。在计算熵和复杂度时，一般同 近年来由符号动力学理论发展出来的符号时间序列分析方法相联系。符号时间序列分析 实质是结合混沌时间序列分析和信息理论的一种分析方法. 其实质是先对序列值的符 号化，符号化后编码，编码后计算熵或复杂度等特征。数据符号化的基本思想就是在几 个可能值上对时间序列进行离散化，把许多可能值的数据序列变换为仅有几个互不相同 值的符号序列。 这是一个“粗粒化”(Coarse-grained)过程，这一过程能够捕获大尺 度的特征，从而降低动力学噪声和测量噪声的影响。而且，复杂度和熵不仅适用于混沌 时间序列，也适用于性质未知时间序列的特征提取和分析。 本文主要研究了时间序列的常用符号化过程，编码序列或原始时间序列的熵和复杂 度的计算。本章中各节主要内容如下：6.2节介绍了时间序列的几种常用符号化方法；6.3 节－6.10节介绍了各种熵的定义、计算方法和应用；6.11节为Lempel-Ziv复杂度的计算、 应用和物理意义分析；6.12介绍了一种计算两时间序列相似度的方法；6.13节为海杂波 的熵和复杂度及其应用；6.14节为本章小结。 6.2 时间序列符号化方法 对于非线性时间序列复杂度的研究，时间序列粗粒化的方法有：均值法、一阶差分 法、移动均值一阶差分法等，这些方法共同的特征是把时间序列简化成容易处理的符号 序列[1-4]。目前采用较多的是如图 1 所示的均值化方法，即对于某一时间序列 x i ( ), = ，令: 1, 2, n i , ave S = ( 1 n = ∑ x i ( ) n = i 1 ) aveX 是一个与时间序列 ( ), s x i n is x i 相同的空符号串。当时间序列中的某一元素 ( ) 为这一时间序列的平均值, = 长度 X> 时，则取符号 为“1”，否则为 s s 1 2 1, 2, (6.1) X , n ave i “0”,由此建立的符号序列为 。由于只考虑大于平均值和小于等于平均值这两种状态, S 所以在动力学结构分析中,这种划分方法对噪声不敏感。而且只能体现出序列的整体特 性，不能体现出序列的局部特性。 - 2 -
    Static transformation (fixed partition) Mean Value 1 0 Symbol Series 1 0 1 0 1 1 0 1 0 1 图表 6-1：连续模拟序列的静态均值符号序列化方法示意图 显然，以上取均值处理的方法存在明显缺陷，大量的细节信号被抹掉。为了体现时 间序列的细节信息，可以使用一阶差分方法符号化时间序列。对一时间序列，任意点与 其前一点进行比较，大于等于前者，记为 1，否则记为 0，得到的符号序列中的所有“01” 或“10”对应一次局部极值。如图表 6-2所示，这种方法在很大程序上提取了信号中的 细节成分。 D yn am ic transform ation (first differen ce) U p = 1 D ow n= 0 S ym bol S eries 0 1 0 1 0 0 1 0 1 0 图表 6-2：连续模拟序列的一阶差分符号序列化方法示意图 N 另外，为了综合上面两种方法的优点，也可动态符号化时间序列。动态符号化是指 对长度为 的时间序列取长度为 的矩形窗，对窗内序列取均值， 窗内大于均值的点 置于 1，小于均值的点置为 0，这样将一长度为 的非“0，1”序列变换为 个 N L− + 个序列分别计算其复杂度或熵，从而得 长度为 的“0，1”符号序列，然后对 到复杂度随时间的动态变化。使用这种方法简单方便，不仅考虑了全局特征也提取了局 部细节信号。 N L− + L 1 L N 1 -3 -
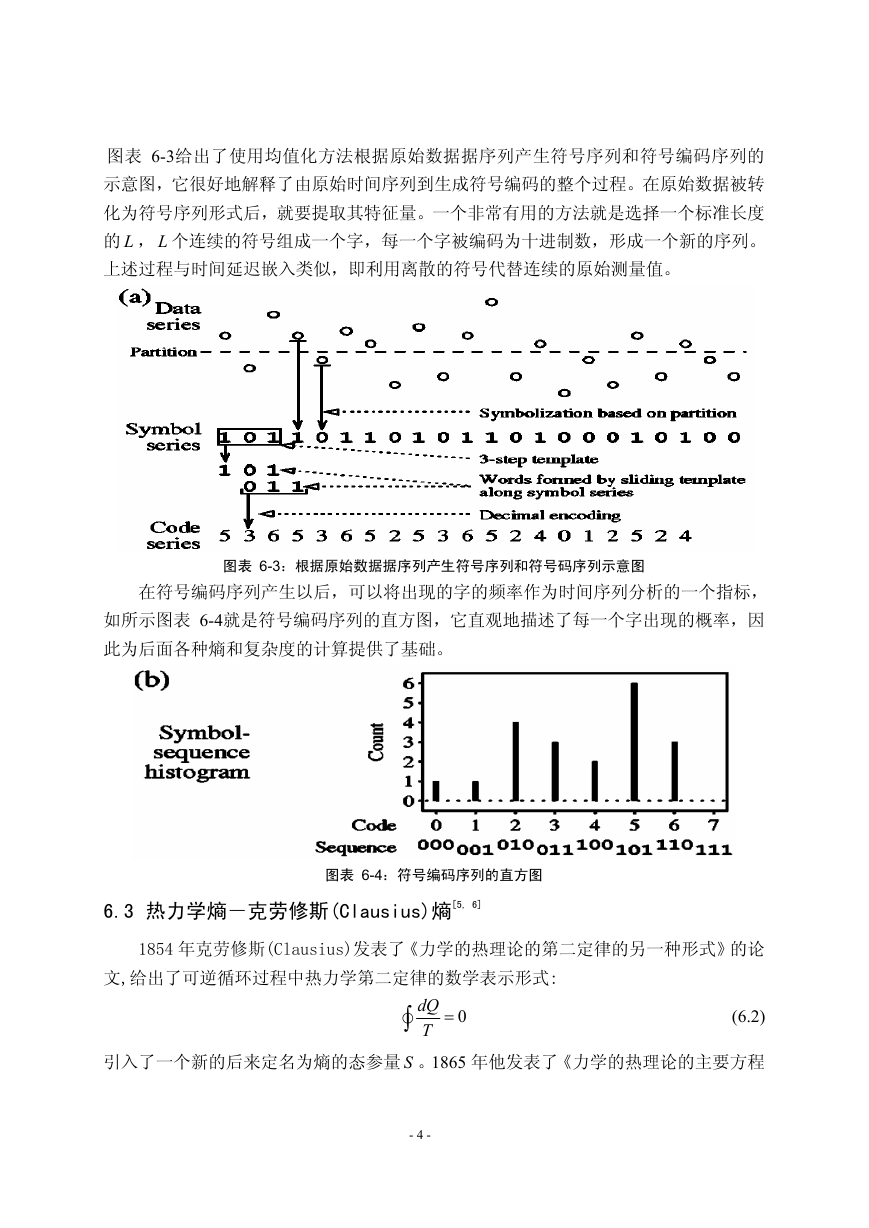
    图表 6-3给出了使用均值化方法根据原始数据据序列产生符号序列和符号编码序列的 示意图，它很好地解释了由原始时间序列到生成符号编码的整个过程。在原始数据被转 化为符号序列形式后，就要提取其特征量。一个非常有用的方法就是选择一个标准长度 L L 的 ， 个连续的符号组成一个字，每一个字被编码为十进制数，形成一个新的序列。 上述过程与时间延迟嵌入类似，即利用离散的符号代替连续的原始测量值。 图表 6-3：根据原始数据据序列产生符号序列和符号码序列示意图 在符号编码序列产生以后，可以将出现的字的频率作为时间序列分析的一个指标， 如所示图表 6-4就是符号编码序列的直方图，它直观地描述了每一个字出现的概率，因 此为后面各种熵和复杂度的计算提供了基础。 6.3 热力学熵－克劳修斯(Clausius)熵[5, 6] 图表 6-4：符号编码序列的直方图 1854 年克劳修斯(Clausius)发表了《力学的热理论的第二定律的另一种形式》的论 文,给出了可逆循环过程中热力学第二定律的数学表示形式: 引入了一个新的后来定名为熵的态参量 。1865 年他发表了《力学的热理论的主要方程 dQ T = 0 (6.2) ∫ S - 4 -
    之便于应用的形式》的论文，把这一新的态参量正式定名为熵。并将上述积分推广到更 一般的循环过程，得出了热力学第二定律的数学表示形式： ∫ dQ T ≤ 0 (6.3) 其中等号对应于可逆过程，不等号对应于不可逆过程。在热力学过程中，为了描述不可 逆过程的单向性，引入态函数熵 。对于只有热接触的封闭系统，熵变化 为 dS S 或 dS ≥ dQ T S a − S b ≥ ∫ bS b a dQ T (6.4) (6.5) (6.6) (6.7) (6.8) b 上式中的 a 、 表示始末两个状态， 、 为始末两个状态的熵， 为系统吸收的热 量， 为热源的温度，可逆过程中T 也是系统的温度。 T 当系统经历绝热过程或系统是孤立的时候，系统与外界没有热量交换： dQ = 0 dQ aS 因此有 或 dS ≥ S− b 0 0 ≥ S a 即有“熵增加原理”：孤立系统或绝热过程是不可逆系统，熵总是增加的。 可逆过程只能沿熵增加的方向进行，最终达到平衡状态。由于系统的无序程度与熵 值存在对应关系，所以由“熵增加原理”导致的孤立系统达到的平衡态是均匀无序状态。 由此定义的熵称克劳修斯熵，或热力学熵。 熵是一个态函数，是热力学宏观量。对绝 热过程和孤立系统中所发生的过程，由熵函数的数值可判定过程进行的方向和限度。 对于非平衡的开放系统，Prigogine 等进一步推广熵的概念，将 表示为 ed S 其中 表示与外界交换能量与物质时，引起熵变换，称为熵交换； 表示系统内部 d S d S e i id S (6.9) dS = + dS 的不可逆过程产生的熵。根据式 (6.9)，对于开放系统有 id S ≥ 0 <若 d S e 0 ，且有 d S e d S i> 则由式(6.9)知，系统有 dS < 0 (6.10) (6.11) (6.12) 即开放系统的熵的总变化是负的，故开放系统有可能形成有序结构。有序结构的形成， 一方面需要外界条件，这是必要的；另一方面需要内部条件，这是充分的。由外界的能 量或物质维持一种空间或时间上的有序结构，称为耗散系统。 -5 -
    Prigogine 等还证明，相对于定态熵的二级偏差(超熵)总是负的，即 (6.13) 超熵对时间的导数称为超熵产生，其值可取不同的符号，据稳定性理论有以下三种情形： Sδ < 0 2 d (1) 当 ( dt d (2) 当 ( dt d (3) 当 ( dt 0 ) ) ) δ < 时，定态是渐近稳定的 2 S δ > 时，定态是不稳定的 2 S 0 δ = 时，定态是临界稳定的 2 S 0 由系统的状态变量和动力学参量决定取三种定态情况中的哪一种。在接近平衡态区 域，已知定态应该是渐近稳定的；当变量变化使状态远离平衡时，系统可能越过(3)的 情形进入(2)的情形。此时均匀无序的定态变成不稳定的，从而通过分叉过程造成对称 的破缺，并出现有序结构(如极限环和混沌)，即有序结构只可能在远离平衡态的非线性 区域出现。 6.4 统计熵－玻尔兹曼(Boltzmann)熵[5] 1896 年，玻尔兹曼(Boltzmann)建立了熵 和系统宏观态所对应的可能微观态数目W S (即热力学概率) 的联系： (6.14) 1900 年普朗克( Planck)引进了比例系数 k －称为玻尔兹曼常量，写出了玻尔兹曼－ W∝ ln S 普朗克公式： (6.15) 所定义的熵称为玻尔兹曼熵，或统计熵。由此玻尔兹曼表明了熵 是同热力学概率W 相 联系的，揭示了宏观态与微观态之间的联系，指出了热力学第二定律的统计本质：熵增 k W ln = S S 加原理所表示的孤立系统中热力学过程的方向性，正相应于系统从热力学概率小的状态 向热力学概率大的状态过渡， 平衡态热力学概率最大， 对应于 取极大值的状态；熵 自发地减小的过程不是绝对不可能的，不过概率非常小而已。 S 6.5 信息熵－先农(Shannon)熵[5, 7] 通常认为，熵概念泛化的最早领域是信息论领域。Shannon 在 1948 年定义了信息熵 作为某件事件不确定度的最度。信息是信息论中一个重要的基本概念，从信息接收者的 角度来看，“信息是能够减少或消除不确定性的一种客观存在和能动过程”。不确定性 是一切客观事物的属性，当接收者未收到某事物的信息之前，对事物的认识是不确定的， - 6 -
    一旦收到信息，就了解了该事物，即可以说对它的认识上的不确定性减少或消除了。那 么我们应该怎么样度量信息呢？关于信息的度量，首先是 Shannon 在通信领域进行研究 的，他建立了由信源(信息的发送者)，信道与编、译码器，信宿(信息的接收者)组成的 通信系统模型，而信息量就是解除信源不确定度所需的信息度量，或者说获得这样大的 信息量后，信源不确定度就被解除。Shannon 以概率和数理统计为工具，提出度量信息 量的数学公式，对于离散型信源，当它由若干随机事件所组成时，随机事件出现的不确 定度用其出现的概率来描述。事件出现的可能性愈小，概率就愈小，而所含信息量却愈 大;相反，事件出现可能性愈大，概率就愈大，而所含信息量却愈小，所以信息量可用事 H 件出现概率的单调减函数来表示，若各事件概率分布不等，则信源提供的平均信息量 即为： H n = −∑ i 1 = p i log ip (6.16) 上式就是信息熵，也称 Shannon 熵。其中， ip 为第 个符号出现的概率，且有 i n =∑ p i i 1 = 1 (6.17) 由符号编码序列直方图可得到反映符号序列总体特征的统计量－Shannon 熵。在二 进制符号化规则下，可定义长度为 的 Shannon 熵为 ( ∑ H L ( ) P s s 1 2 = − ln L s L s 1 ln 2 L P s s 1 2 )L s (6.18) 式中， P 为长度为 的短符号序列经二进制至十进制变换得到序列编码后，在 s s 1 2 L s L 直方图中出现的各个符号编码所对应的概率。 通过式(6.16)可以看出，信息熵是从平均意义上描述信源的总体特征的，它表 示信源输出的平均信息量，它表征信源的平均不确定性。控制论的主要创立者Wienner 曾说；“信息量是一个可以看做概率的量的对数的负数，它实质上是熵。”这实际上推 广了原来热力学熵的概念。信息熵越大，说明信号源发出的平均信息量越大，即信源的 不确定度大；而热力学概念的熵，是系统不确定性或无序度的量度。可见，信息熵与热 力学概念的熵在性质上是等同的，所以我们可以说信息熵是热力学熵的自然推广。通过 这种概念的扩展，我们可以看出：熵不仅不必与热力学过程相联系，而且也不必与微观 分子运动相联系，它可以成为系统状态不确定程度的度量，这个状态可以是热力学的， 也可以不是热力学的；可以是微观的，也可以是宏观的。 在熵的泛化当中，我们得到信息熵的表达式为式(6.16)，它把概率分布函数与熵联 系起来，即每一个概率分布对应着唯一的一个信息熵值。也就是说，一个信息熵值表达 -7 -
    了一个概率分布的不确定性程度。进一步推广，如果用满足式(6.17)条件的非概率分布 函数来代替上式中的概率分布函数，结果会如何？事实上，从数学上讲，只要是满足了 式(6.17)的分布函数，无论它是否是概率分布函数，并没有这方面的要求。所以，由式 (6.17)的各种不同形式，发展起来各种熵的定义形式。 6.6 Kolmogrov 熵和 K2 熵 1958年Kolmogrov定义了测度熵，称为Kolmogrov熵(又称信息维数)，用来度量系统 运动的混乱或无序的程度。随后Sinai进行了改进，所以又称为Kolmogrov-Sinai熵，简称 为K-S熵。考虑一个 维动力系统，将它的相空间分割成一个个边长为 ε的 维立方体盒 ( )x t ，取时间间隔为一很小量 子，对于状态空间的一个吸引子和一条落在吸引域的轨道 表示起始时刻轨道在第 个格子中，t τ= 时在第 个格子中的联合 n n di 0i i 1, ( 0 P i τ，令 概率，则Kolmogorov熵定义为： i ) , d , K = − lim lim lim → → →∞ τ ε d 0 0 1 d τ ∑ i d i 0 ( P i 0 , i 1 , , i d ) ln ( P i 0 , i 1 , )d i , (6.19) 而 阶Renyi熵定义为 q K q = − lim lim lim → → →∞ τ d 0 0 l 1 d q τ 1 − 1 log 2 ∑ i d i 0 q ( P i 0 , i 1 , ) i d , (6.20) 由于K-S熵的计算非常复杂，早期的定义主要是直接从定义入手，进行了一些研究， 这些研究虽然很有意思，但不很成功。Crassbreger和Procaccia于1983年提出了相关维数 的概念[8]，并定义了相关熵(Correlation Entropy)的概念来逼近Kolmogorov熵[9]，简写为 2K 熵， 熵和关联积分 2K dC l 2( ) 存在如下关系： 0 r 0 2 d K = − limlim lim log → → →∞ τ 1 d τ 对离散时间序列，固定延迟时间τ，式(6.21)为 1 dτ 时与 存在如下关系： C r lim ( ) 2 d r → 关联积分 lim lim log r → →∞ dC r 2( ) r → = − D 2 在 ∝ K 0 r r 0 d 2 0 2 C r ( ) 2 d 2 C r ( ) 2 d 其中， 2D 为关联维数， 为尺度。结合式 (6.22)和式(6.23)有 C r lim lim ( ) 2 d r →∞ →∞ r d D 2 K d τ− 2 = d r - 8 - (6.21) (6.22) (6.23) (6.24)
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料